地震作用下回填砂地基沉入式钢圆筒防波堤变形机理分析
2019-01-23冯国俊
冯国俊,宋 波 ,王 荣
(1. 北京科技大学 土木与资源工程学院,北京 100083;2. 强震区轨道交通工程抗震研究北京市国际科技合作基地,北京 100083;3. 中国港湾工程有限责任公司,北京 100027)
沉入式钢圆筒结构是无底无内隔墙的大直径薄壁圆筒结构,内部填充砂土等材料,适用于防波堤或岸壁等港口结构选型,场地适应能力强,适合于深水区,且施工周期短安全性高。目前钢圆筒岸壁逐渐在国内外得到广泛应用,但钢圆筒防波堤在国内外应用较少,我国采用沉入式钢圆筒结构的港口结构包括广州番禺南沙蒲洲海堤护岸工程和港珠澳大桥人工岛工程等。当地震发生时,钢圆筒防波堤和岸壁等港口结构会由于地基变形导致其倾斜、滑移,甚至倾覆,例如1995年日本兵库县地震导致摩耶码头钢圆筒岸壁产生1~4 m的水平残余位移,输送货物的机械设备失效[1]。因此,开展沉入式钢圆筒防波堤变形机理研究有着重要的现实意义。
国内外学者针对地震作用下港口结构变形等方面开展了不少研究工作,Ozutsumi等[2]通过有效应力分析法研究了河堤由于液化导致的变形;菅野高弘等[3]基于振动台试验研究了钢圆筒岸壁的地震响应;方云等[4]通过振动台试验研究发现地震时重力式码头以侧向运动为主,李炎保等[5]在总结国内外防波堤发展基础上开展了其损坏原因分析;王丽艳等[6]开展了砂性地基防波堤地震残余变形机制研究;王桂萱等[7]采用数值模拟分析了田湾核电防波堤动力特性。本文将通过振动台试验和数值模拟研究回填砂地基沉入式防波堤的动力响应影响,并分析防波堤的变形机理。
1 有限差分模型动力响应影响分析
1.1 工程背景
委内瑞拉卡贝略港防波堤采用沉入式钢圆筒结构,分东堤和西堤(见图1),由一系列钢圆筒结构组成,钢圆筒之间通过混凝土膜袋相连,间距为1 m。防波堤典型断面和平面布置,如图2所示,钢圆筒直径22 m、壁厚16 mm、高22.5 m,筒顶标高+2.5 m,筒底标高-20 m,钢(Q345)屈服强度为34 5MPa。筒内外砂为回填砂,筒底砂主要为密实的细砂。防波堤按《港口结构抗震设计指南》[8]基于超越概率50%(Level 1)和超越概率10%(Level 2)进行抗震设计,对应设计地震动分别为1.7 m/s2和3.2 m/s2。为防止回填砂地基液化,计划对筒内外回填砂进行改良。

图1 防波堤示意图Fig.1 Diagram of breakwater

(a) 典型断面

(b) 平面布置图2 防波堤典型断面和平面布置示意图Fig.2 Diagram of typical section for breakwater
1.2 有限差分模型
为更合理地开展数值模拟和振动台试验,需要对工程实际结构进行简化。由图2(b)平面布置图可以看出,由于钢圆筒防波堤沿切线方向连续排列布置,各个钢圆筒是相对独立的,因此可取单个圆筒开展数值模拟和振动台试验。同时由于钢圆筒之间的相互作用,切线方向地震对钢圆筒影响非常小,对钢圆筒防波堤影响较大的是法线方向地震。因此采用FLAC3D沿防波堤法线方向建立的三维模型如图3(a)所示,模型长为242 m,防波堤两侧采用5倍钢圆筒直径土体,高为38.5 m,其中筒内回填砂高为22.5 m,筒底砂高度为16 m,宽为23 m,设置自由场边界条件,如图3(b)所示。钢圆筒采用结构壳单元,不同土层参数如表1所示,回填砂和筒底砂采用Finn本构模型,采用link来使钢圆筒结构单元和土体单元产生相互作用,同时采用渗流模式,实现流固耦合。

(a) 模型

(b) 自由场边界条件图3 防波堤有限差分模型Fig.3 Finite difference model of breakwater表1 不同土层参数Tab.1 Parameters of different soil layers

参数干密度ρ/(kg·m-3)体积模量K/MPa剪切模量G/MPa泊松比ν黏聚力c/(kN·m-3)内摩擦角ϕ/(°)渗透系数k/(cm·s-1)孔隙率n阻尼比ζ液化参数回填砂1 500133.3361.540.32285×10-30.450.05Dr=20%C1=4.25C2=0.24筒底砂1 800510235.380.34421×10-30.40.05Dr=80%C1=1.75C2=2.29注:液化参数根据Byrne等[9]研究成果确定,其中C1=007 6Dr-2.5,C2=0.4/C1, Dr根据《工程地质手册》(第四版) [10]确定。式中:Dr为砂土相对密度;C1和C2为液化参数
1.3 地震波选择
选择1940年美国帝王谷地震(简称El地震波)、1983年日本海地震(简称T1地震波)和1995年日本兵库县地震(简称T2地震波)作为水平向输入地震波,其中El地震波和T2地震波属于近场地震,T1地震波属于远场地震,分别按加速度峰值为1.7 m/s2和3.2 m/s2加载,地震波特性如表2所示,加速度峰值为1.7 m/s2时的各地震波加速度时程曲线,如图4所示。

表2 地震波特性Tab.2 Characteristics of seismic waves

图4 加速度时程曲线Fig.4 Time-history curves of acceleration
1.4 动力响应影响分析
钢圆筒结构包括钢圆筒和筒内回填材料,由于钢圆筒内部有回填砂等土体,导致钢圆筒结构刚度较大,可将钢圆筒结构看作刚体[11]。防波堤变形模式主要由钢圆筒结构和地基条件决定,因此沉入式防波堤典型变形模式如图5所示。当地基为图5(a)坚实的地基时,防波堤以水平运动为主,产生较小的水平位移,当地基为图5(b)松散砂地基时,防波堤严重倾斜,产生较大的水平位移。由于钢圆筒防波堤损伤程度由顶部水平残余位移大小和钢圆筒应力状态决定,二者是钢圆筒结构和地基条件变化的综合反映,因此在动力响应影响分析过程中将重点分析防波堤顶部水平残余位移和钢圆筒应力。

(a) 坚实的地基

(b) 松散砂地基图5 防波堤典型变形模式Fig.5 Typical deformation modes of breakwater
采用弹塑性求解法生成初始地应力场,通过流固耦合施加水压力荷载达到平衡,施加自由场边界条件模拟自由场地,然后加载不同加速度峰值大小的地震波开展动力分析,数值模拟后发现当加载加速度峰值为1.7 m/s2时的地震波时筒外回填砂未发生液化,当加载加速度峰值为3.2 m/s2时的地震波时筒外回填砂发生液化。由于当进行动力分析时,防波堤顶部水平位移包括地基土体位移和防波堤顶部水平残余位移(见式(1)),因此通过数值模拟可得到加载加速度峰值为3.2 m/s2时的El地震波时网格变形,如图6所示,顶部产生的水平位移约为0.54 m。由于防波堤筒底回填砂为密实的细砂,筒内外为回填砂,回填砂与筒底砂之间的作用力阻碍了防波堤的运动,因此防波堤产生的水平位移较小。同时可得到加载El地震波时防波堤水平位移时程曲线,如图7所示。由图7可以看出,随着地震波时间的持续,防波堤顶部水平位移逐渐增大。
w=d+d′
(1)
式中:w为防波堤顶部水平位移;d为防波堤顶部水平残余位移;d′为地基土体位移。

图6 有限差分模型网格变形图Fig.6 TheFigures of mesh deforming for finite difference model

(a) El地震波加速度峰值1.7 m/s2

(b) El地震波加速度峰值3.2 m/s2图7 El地震时防波堤水平位移时程曲线Fig.7 Time-history curves of residual horizontal displacement for breakwater under El seismic waves
通过动力分析可得到加载不同地震波时防波堤顶部水平残余位移,如图8所示。由图8可以看出,当不同地震波作用于防波堤时,顶部水平残余位移方向不同,使防波堤朝海侧或岸侧方向运动,这是由于地震波加速度方向不断变化造成的。同时可以看出,当地震波加速度峰值为1.7 m/s2时,近场地震和远场地震对防波堤筒顶水平残余位移影响较一致,但当地震波加速度峰值为3.2 m/s2时,远场地震对防波堤筒顶水平残余位移影响比近场地震时大。因此,当地震波加速度峰值较小时,近远场地震对防波堤的动力响应影响较一致,但当地震波加速度峰值较大时,远场地震比近场地震对防波堤动力响应影响要大,主要是地震波类型为近远场地震所决定的。远场地震对刚度小的地基影响大,近场地震对刚度大的地基影响大,由于回填砂刚度较小,因此远场地震比近场地震对回填砂地基防波堤动力响应影响较大。

图8 不同地震时防波堤顶部水平残余位移Fig.8 Residual horizontal displacement on the top of breakwater for different seismic waves
通过动力分析可得到加载不同地震波时钢圆筒筒壁所受最大应力沿高程变化趋势,如图9所示。由图9可以看出筒底部位(-20 m,点B)应力最大,但在泥面部位(-14 m,点A)出现拐点,说明地震时埋入土内的钢圆筒不断与筒内外土层相互挤压,从而造成接触处的应力较大,泥面以上的钢圆筒由于筒外不受土体约束,导致筒与筒外土层地表接触处应力较小。因此钢圆筒防波堤筒壁存在两处应力较大的薄弱环节,分别位于筒底部位(点B)及泥面部位(点A),因此应将点A和点B作为结构断面设计的控制部位。同时可以发现当加速度峰值为3.2 m/s2时T1地震波导致筒壁应力响应影响最大,此时筒壁底部(点B)最大应力约为289 MPa,泥面处(点A)最大应力约为249 MPa,说明钢圆筒尚未进入塑性。

图9 钢圆筒应力最大值沿标高变化Fig.9 Change of maximum for stress of steel cylinder along the elevation
1.5 防波堤抗震性能设计极限值分析
《港口结构抗震设计指南》中未提及对钢圆筒防波堤设计指标,但将钢圆筒岸壁标准化水平残余位移和应变作为设计的控制指标。同时日本《沉入式钢圆筒结构工法 设计·施工指南》将钢圆筒结构标准化水平残余位移<1.5%作为设计控制指标。由于钢圆筒岸壁和钢圆筒防波堤都属于钢圆筒结构,同时有着相同的设计控制指标,所以可参考钢圆筒岸壁的抗震性能指标建立钢圆筒防波堤的抗震性能指标,因此将防波堤顶部标准化水平残余位移1.5%(式(2)和式(3))和钢圆筒应力345 MPa作为防波堤抗震性能控制极限值。因此,当防波堤泥面以上高度h=16.5 m,防波堤顶部水平残余位移为0.247 5 m。通过数值模拟可得到加载加速度峰值为3.2 m/s2的地震波时防波堤震性能控制极限值分析结果,如表3所示。由表3可以看出,当加载不同地震波时,钢圆筒应力极限值小于345 MPa,T1地震波时顶部标准化水平残余位移大于极限值1.5%,此时水平残余位移超过0.247 5 m的抗震性能控制极限值,钢圆筒未达到塑性,因此防波堤破坏模式主要由水平残余位移决定。
(2)
H=h+h′
(3)
式中:δ为防波堤顶部标准化水平残余位移;h为泥面到防波堤顶部的距离;h′为泥面到防波堤底部的距离;H为防波堤高度。

表3 抗震性能设计极限值分析结果Tab.3 Analysis results of design limit for seismic performance
由于钢圆筒结构在工程实际中通常通过拱弧部将多个钢圆筒相连,通过MIDAS-GTS NX软件建立与单筒模型地质条件相同的三筒相连防波堤模型,如图10(a)所示,长为242 m,宽为69 m,采用黏弹性边界条件,液化模型采用修正UBCSAND模型[12-13],通过数值模拟得到加载加速度峰值为3.2 m/s2的T1地震波时模型切线方向位移云图,如图10(b)所示。由图10(b)可以看出防波堤顶部水平位移约为0.790 m,水平残余位移约为0.342 m,则此时防波堤顶部标准化水平残余位移约为2.073%,大于极限值1.5%,且与单筒模型计算结果比较接近。同时,通过相同地质条件下三筒相连防波堤模型(原型和模型的相似比为λ=73.3)的振动台试验(见图10(c))得到加载T1地震波时防波堤顶部水平位移(中间筒位移测点u1)约为0.949 m,与单筒模型数值模拟结果相差约14.34%。另外,通过数值模拟可得到T1地震波时中间筒应力最大值沿标高变化变化情况如图10(d)所示,且筒壁底部最大应力约为261 MPa,与单筒模型计算结果相差约9.69%。因此单筒模型计算结果比较合理。

(a) 三筒相连防波堤模型

(b) T1地震波时防波堤切线方向位移云图

(c) 三筒相连防波堤振动台试验示意图

(d) T1地震波时中间筒应力最大值沿标高变化图10 钢圆筒防波堤模型及分析结果Fig.10 Model and analysis result of steel cylinder breakwater
2 振动台试验研究
2.1 模型相似关系
为分析沉入式钢圆筒防波堤在地震作用下的动力响应影响,开展振动台试验时需要考虑土-结构-流体的相互作用。Iai[14]通过理论分析了土-结构-流体相互作用,并结合香川崇章等[15-16]取得的研究成果,提出了适用于考虑土-结构-流体相互作用时分析砂土液化的1 G重力场振动台试验相似关系,并在港口结构试验方面得到广泛应用。取防波堤原型和模型的相似比为λ=27.5,则根据Iai的研究成果得防波堤原型和模型相似系数,如表4所示。

表4 防波堤原型和模型相似比Tab.4 Ratio of similitude for prototype and model of breakwater
2.2 模型设计及测点布置
防波堤振动台试验如图11(a)所示,振动台台面尺寸为1.5 m×1.5 m,模型箱为2 m×1 m×1.5 m(长×宽×高)的钢板箱,三个侧面采用钢板,一个侧面采用透明有机玻璃板,模型箱底部与振动台台面依靠螺栓固结。在箱体和土体之间采用柔性材料海绵填充,模拟地震波的边界条件,模型边界条件如图11(b)所示。同时采用如图11(c)所示的透明有机玻璃做单筒模型(见表5),并在筒内外和筒底选用与工程现场密度相同的细砂来模拟回填砂和筒底砂。其中振动台试验有机玻璃模型参数是根据实际钢圆筒结构由几何相似和抗弯刚度相似确定的。模型测点布置如图11(d)所示,设置超孔隙水压力测点P1,P2,P3,P4和P5,加速度测点a1,a2,a3,a4和a5以及顶部水平位移测点u1。

表5 有机玻璃模型参数Tab.5 The parameters of organic glass model

图11 防波堤振动台试验Fig.11 Shaking table test of breakwater
砂性土级配对液化的难易程度影响很大,当砂土颗粒越细时,越容易液化。工程现场回填砂和筒内外试验用回填砂的颗粒级配分布曲线,如图12所示,颗粒分析结果表明工程现场和试验粗粒土(>0.075 mm)含量均超过85%,级配曲线相近,通过上述分析表明试验可很好模拟工程现场情况。

图12 回填砂颗粒级配曲线Fig.12 Grain composition of backfill sand
2.3 试验加载方案
试验选择加速度峰值为3.2 m/s2的El地震波、T1地震波和T2地震波为台面水平方向输入地震波,地震波持续时间按相似比进行压缩。由于输入加速度峰值为3.2 m/s2的El地震波后回填砂地基发生液化,防波堤产生不可逆变形,所以未进行T1地震波和T2地震波工况试验。
2.4 试验现象分析
通过试验可得到不同测点超孔隙水压力变化,如图13所示。由图13(a)看出,筒内测点P1和筒外测点P2超孔隙水压力随加速度峰值的增大迅速上升,当超过土体初始有效应力时持续一段时间,然后开始缓慢下降,说明测点P1和测点P2部位的砂土在地震动激励下已经液化,且液化后超孔隙水压力在逐渐消散。同时由图13(b)看出,测点P3,P4和P5超孔隙水压力未超过土体初始有效应力,且未出现明显的下降趋势,因此上述测点未液化。同时,由于筒内回填砂测点P1部位已经液化,而测点P3部位未液化,因此位于水中的筒内回填砂上部已经液化,下部未液化。由于位于水中的筒内回填砂上部已液化部分上部为渗透性好的砂层,所以在液化的过程中,已液化部分筒壁受到的压力将减小,水将逐渐溢到水位线上回填砂部分。但在液化后,由于砂将变得比较密实,此时对筒壁的压力将增大。因此,通过试验可以发现,钢圆筒位于水中的回填砂上部已经液化,下部未液化,且钢圆筒液化部分受力将先减小后增大。

(a) 测点P1和P2

(b) 测点P3,P4和P5图13 测点超孔隙水压力时程曲线Fig.13 Time-history curves of excess pore water pressure for measuring point
筒外回填砂测点P2附近回填砂液化产生的滑移现象,如图14(a)所示,表明筒外回填砂地基发生液化滑移现象。且由于回填砂液化导致筒外回填砂对防波堤的侧向作用减小,筒身发生偏转,产生的试验现象如图14(b)所示,符合图5(a)变形模式。因此筒外回填砂对防波堤的稳定性起到关键作用,需要优先对筒外回填砂地基进行改良,防止回填砂液化。

图14 振动台试验现象Fig.14 The phenomena of shaking table test
2.5 振动台试验与数值模拟结果对比分析
通过振动台试验和数值模拟可得到加载加速度峰值3.2 m/s2的El地震波时筒壁水平加速度最大值沿筒高的变化,如图15所示,筒壁顶部加速度测点J1的加速度时程,如图16所示。由图15可以看出,筒壁水平加速度最大值沿筒高不断增大,其中试验时筒壁顶部测点水平加速度最大值达到约6.2 m/s2,与数值模拟结果相差约12.93%。由图16可以看出筒壁顶部加速度峰值出现的时间要晚于El地震波加速度峰值出现的时间。同时可得到振动台试验和数值模拟时筒壁顶部水平位移,如图17所示,其中试验结果与数值模拟结果相差约16.14%,说明试验结果与数值模拟结果较一致。

图15 筒壁水平加速度最大 值沿标高变化情况Fig.15 Changes of maximum for horizontal acceleration of cylinder wall along the elevation

图16 防波堤顶部加速度时程曲线Fig.16 Time-history curves of horizontal acceleration on the top of breakwater
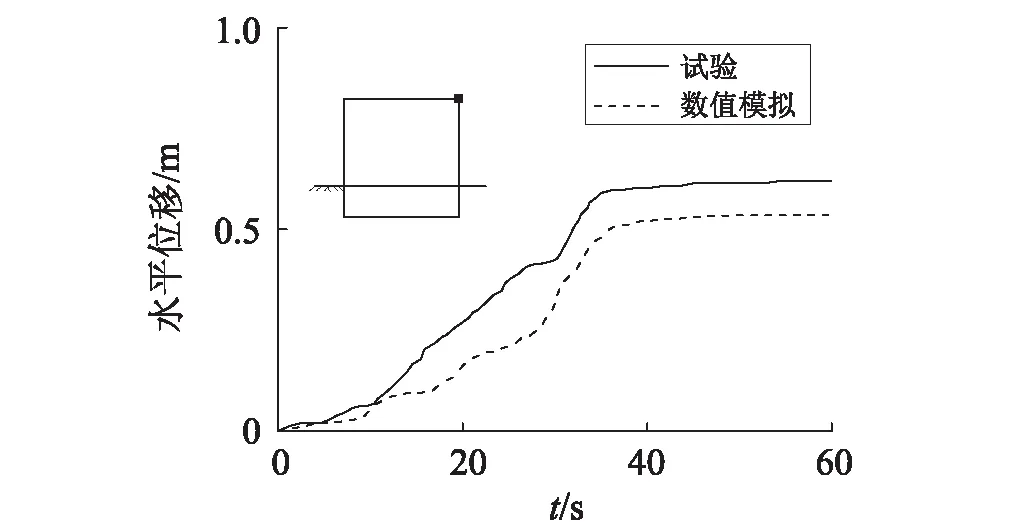
图17 防波堤顶部水平位移时程曲线Fig.17 Time-history curves of horizontal displacement on the top of breakwater
3 结 论
(1) 振动台试验表明当加载加速度峰值为3.2 m/s2的El地震波时,由于地震波作用筒外回填砂液化,导致筒外回填砂对防波堤的侧向力改变,防波堤产生倾斜现象,建议优先对筒外回填砂进行改良,防止其液化。
(2) 钢圆筒防波变形模式主要由钢圆筒结构和地基条件决定,由于钢圆筒结构刚度较大,筒底砂为密实的细砂,筒外砂为比较松散砂,该钢圆筒防波堤以水平运动为主,筒外回填砂对钢圆筒稳定性起到关键作用。
(3) 抗震性能控制极限值分析表明当加载加速度峰值为3.2 m/s2的T1地震波时,该防波堤水平残余位移超过0.247 5 m的抗震性能控制极限值,钢圆筒未达到塑性,处于弹性阶段,因此防波堤损伤程度主要由水平残余位移决定。
(4) 随着加速度峰值的增大,远场地震比近场地震波对防波堤水平残余位移影响较大,同时通过数值模拟研究了钢圆筒应力影响规律,发现该防波堤钢圆筒筒底和泥面处应力较大,为结构的薄弱环节,可为工程设计提供参考依据。
