振动荷载作用下浸水过程对重载铁路基床变形特性影响研究

韩博文， 冯怀平， 应志超， 李立增

(1.石家庄铁道大学 土木工程学院，石家庄 050043；2.神华包神铁路集团有限责任公司，内蒙古 包头 014014；3.石家庄铁路职业技术学院，石家庄 050041)

重载体铁路的运输能力大，有较好的经济效益，发展重载铁路运输是世界各国铁路运输发展的主题之一，我国为增加铁路货运能力，加快了对既有线路的扩能改造升级步伐。预测线路扩能改造后出现的病害，提前制定相应的治理措施是升级改造的一项重要工作。宋绪国等[1]研究表明列车动应力与降雨浸水的联合作用引起基床湿化变形被认为是造成线路不均匀沉降的主要原因。降雨浸水会使基床土体产生湿化变形，湿化变形概念源于土石坝等水利工程，指粗粒料在一定应力状态下浸水，由于颗粒之间被水润滑以及颗粒矿物浸水软化等原因而使颗粒发生相互滑移、破碎和重新排列，从而产生变形，并使土体中的应力发生重分布的现象。研究者对土的湿化变形影响因素进行了深入的研究，应力水平[2-5]对湿化变形有着较为明显的影响，轴向应变随着湿化应力水平的增加而增加，体变随着湿化应力水平的增加而减小；土的湿化变形与土的初始状态，如压实度、初始含水率及基质吸力等有较大关系，刘新喜等[6-10]得出了湿化变形随压实度增加而降低的结论；韦慧等[11]发现变形模量随含水率增加而减小，谈云志等[12]认为湿化变形是由基质吸力丧失而产生，朱元青等[13]研究发现吸力越大黄土湿陷变形越大，毛雪松等[14]发现浸水量和浸水时间对湿化变形影响显著。铁路基床长期受到列车动力荷载的作用，研究者为分析循环荷载作用下路基变形特性进行了大量研究，刘萌成等[15]通过对粉质粘土进行动三轴试验，并针对现有累积变形经验公式的局限性，建立了一个反映多重因素的累积变形预测模型；张向东等[16]、冷伍明等[17]分别研究了循环荷载作用下动应力幅值、围压对累积变形的影响，均发在现净围压一定的条件下，动应力幅值较小时，土样产生弹性变形且变形最终趋于稳定，动应力幅值较大时，经过一定的循环次数后土样达到破坏，在动应力幅值一定的条件下，围压对变形影响显著；冷伍明等[18]还研究了振动荷载下重载铁路路基粗粒填料的临界动应力；尹松等[19]对循环振动作用下残积土滞回曲线、累积塑性应变及骨干曲线的变化规律进行了大量试验研究，成果显著。

实际工程中动应力与浸水湿化作用是同时联合进行的，应该同时考虑动应力与湿化作用的影响。为此，冯怀平等[20]研究了单一浸水过程下基床土体的动力湿化特性。然而，既有线路排水状态及自然条件差异，扩能改造前基床经历了不同的浸水过程，在前期荷载作用下基床的状态也不相同。研究浸水过程对基床在扩能升级后湿化变形影响对有效预测评估不良天气条件下线路的平顺性有重要价值。

为研究不同浸水过程下重载铁路基床的湿化变形特性，利用英国GDS动三轴仪结合恒定水头补水的马氏瓶，模拟了三种浸水过程，在三种过程下进行了振动三轴试验，分析了每种浸水过程对湿化变形、滞回曲线以及软化指数的影响，为既有线路的扩能改造提供更加有价值的借鉴和参考。

1 不同浸水过程的动力湿化试验

1.1 试样物理力学参数

试验的土样来自朔黄铁路原平工务段某路基翻浆冒泥病害较为严重里程，该段为扩能改造的重点加固区段，土质为粉质黏土，属于C类填料，基本物理性质见表1。

1.2 试样制备

试验用土过筛去除杂质，配制成含水率为8%的土样，静置一夜，在击实筒内分4层击实，压实度为0.9，同一组试样的密度差不得超过0.02 g/cm2。

表1 试样物理参数

1.3 试验仪器

本次试验采用能够自动采集数据的英国GDS动三轴仪以及能够以恒定水头补水的马氏瓶如图1、2所示。常水头马氏瓶与大气连通的开口略高于试样底部，将马氏瓶底部利用导管与GDS振动台的通气孔相连通，因为水头差的存在，当向马氏瓶注水后即可实现自行在试样底部补水，并利用阀门开闭来控制补水过程的开始和结束。

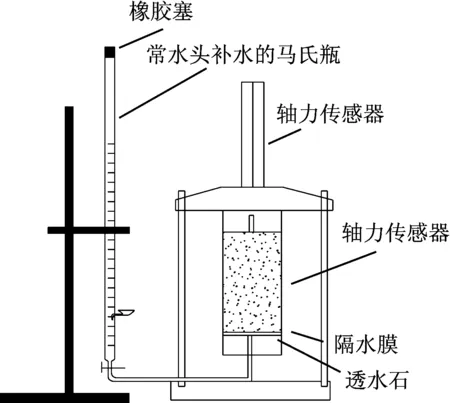
图1 试验仪器示意图

图2 试验仪器实物图

1.4 试验方案

本试验利用常水头马氏瓶在不同阶段补水来模拟不同雨水入渗情况，通过改变加载幅值实现列车扩能改造增加的动荷载，这样使得试验过程更加符合实际情况，共设置了三种浸水过程分别对应三种实际情况：①情况一，基床在扩能改造前受到降雨浸水作用(补水阀门开启)，在扩能改造后(动应力幅值增加)也受到降雨浸水作用(补水阀门开启)；②情况二，基床在扩能改造前不受到降雨浸水作用(补水阀门关闭)，在扩能改造后(动应力幅值增加)受到降雨浸水作用(补水阀门开启)；③情况三，基床在扩能改造前受到降雨浸水作用(补水阀门开启)，在扩能改造后(动应力幅值增加)不受到降雨浸水(补水阀门关闭)作用(后文均用情况一、情况二、情况三代指三种情况)。

该地区长期开行C80型敞车，依据车辆长度和运行速度利用公式计算可确定列车运行时加载到路基上的频率。C80列车车辆长度为12 000 mm，运行速度为100 km/h，利用公式

f=v/l

(1)

可计算出频率约为2.5 Hz，因此本试验依据其现场检测结果确定加载频率为2.5 Hz。苗雷强[21]通过现场动态实测结果表明扩能改造前轴重为25 t的C80列车产生的动应力约为90 kPa，故设置90 kPa动应力进行模拟，扩能改造后轴重将不断增加，因此以100 kPa、110 kPa、120 kPa动应力来模拟扩能改造后轴重。通过文献[21]还可以得到路基的围压一般在25～60 kPa之间，本试验设定围压为30 kPa，每种情况下的试验过程均分为四个阶段，别为前期固结阶段、动力稳定阶段、动力加载阶段、动应力幅值增加阶段，前两个阶段的设置是考虑试样在安装及制样过程中可能存在的不连续以及路基由于施工及前期运营荷载的作用过程，这样使得每个试样在动力加载阶段前的状态基本保持一致，不影响后续试验结果。

每组做三个平行试验，试验加载及湿化过程示意图，见图3。试验完毕后利用电脑收集数据绘制应力应变曲线等相关曲线研究规律，试验过程的详细参数见表2。

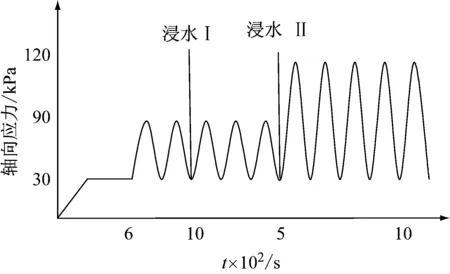
图3 动力湿化过程示意图

试验分组围压/kPa前期固结阶段动力稳定阶段动力加载阶段动应力幅值增加阶段固结时间/min动应力幅值/kPa动应力幅值/kPa湿化情况动应力幅值/kPa湿化情况第1组第2组第3组第4组第5组第6组第7组第8组第9组301090903010909030109090湿化-湿化湿化-湿化湿化-湿化110110120湿化湿化-湿化湿化-湿化湿化-

2 动力湿化试验结果及分析

通过分析三种情况下不同动应力幅值对湿化变形的影响，绘制出湿化过程下应变与振动次数的关系曲线图，如图4～图6所示。

“‘煤炭老板！’我喊道，那急切的声音裹在呼出的热气里，在严寒中显得格外沉浊。”“‘不能马上’这两个词多么像钟声啊，它们和刚才听到的附近教堂尖塔上晚钟的声响混合在一起，又是怎样地使人产生了错觉啊！”

从图4、图5、图6可以看出：第一种情况下在动力加载阶段应变成相同增长趋势，而在动应力幅值增加阶段应变在短时间内随振次显著增长，出现明显转折点，表明因在湿化与更大的动应力作用下土体产生较大应变，随后在很短时间内便达到稳定；第二种情况下在动力加载阶段由于没有浸水湿化故应变很小，增长趋势十分平缓，而在动应力幅值增加阶段同样出现明显转折点，应变在短时间内随振次显著增长，随后增长趋势减小但并未趋于稳定，整个阶段一直保持很大增长趋势，这是由于在前期经历了较长时间的循环荷载作用，使得试样在未浸水的情况下产生了一定累积应变，在载循环荷载作用下试样内部孔隙减小，故开始补水后水分渗透较缓慢，湿化变形发展也就相对较慢，因此应变在试验过程内未达到稳定，需经历更长的应变发展过程，面对这样浸水过程的基床，在前期或许不会产生较大变形，一旦基床浸水之后的很长一段时间内，基床会产生一个持续增长不易稳定的变形，需要引起重视，在实际工程中要注意对基床变形的日常检测；第三种情况下的应变规律与第一种情况大体相似，由于在动应力幅值增加阶段停止浸水使得应变较第一种情况偏小此外还可以明显看出每种情况下应变与动应力幅值的大小成正比。

本试验通过记录不同时刻的浸水量来反映浸水规律，三种情况下的浸水量与时间关系曲线如图7～图9所示。

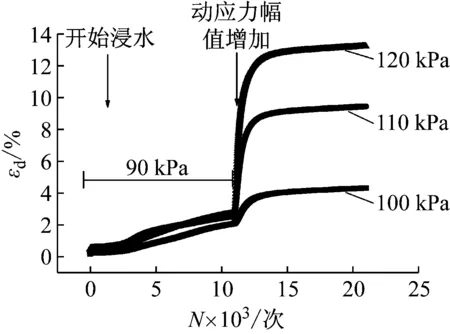
图4 情况一不同动应力幅值下应变- 振次关系曲线

Fig.4 Strain vibration relationship curves under different dynamic stress amplitudes in situation 1

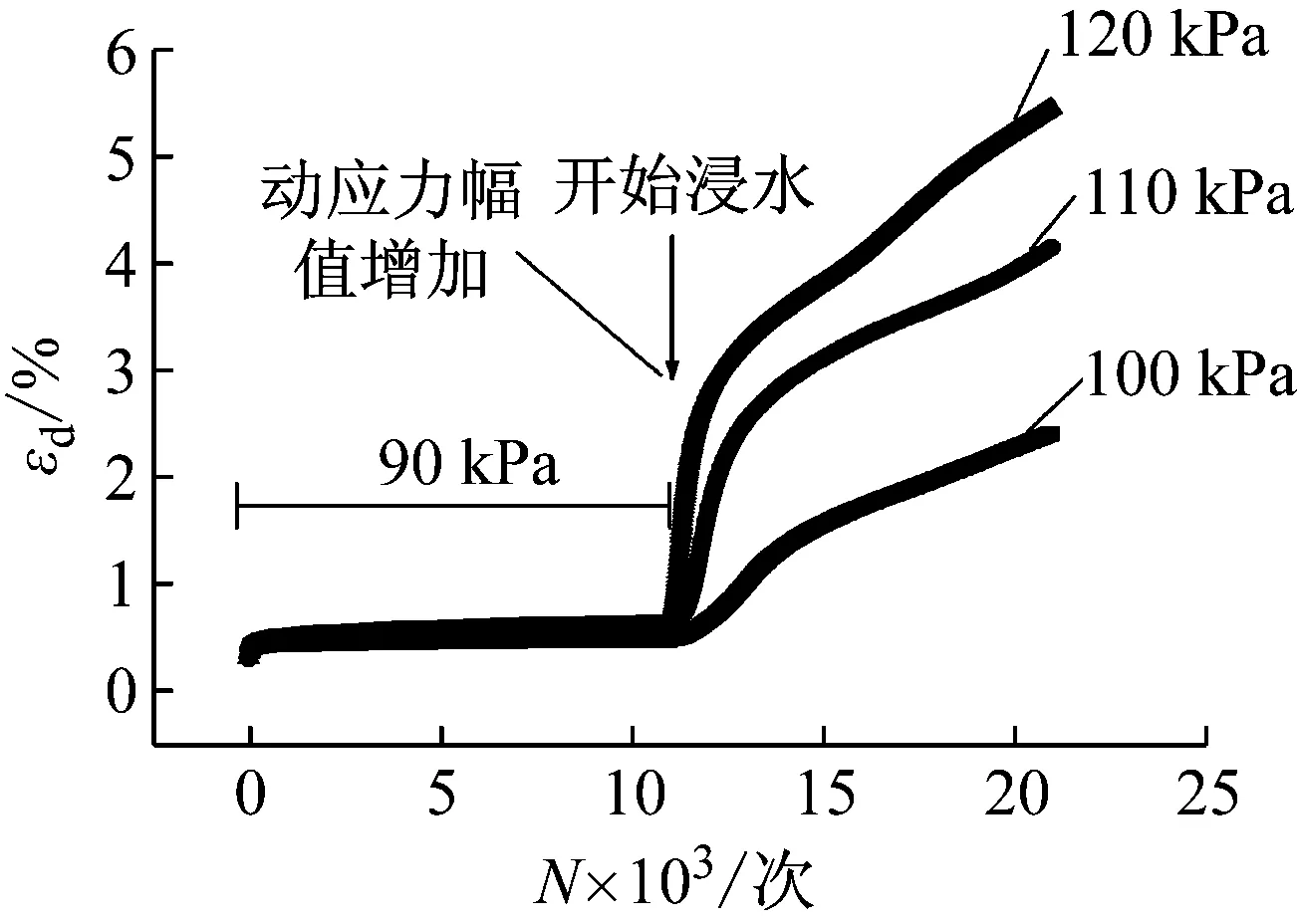
图5 情况二不同动应力幅值下应变- 振次关系曲线

Fig.5 Strain vibration relationship curves under different dynamic stress amplitudes in situation 2

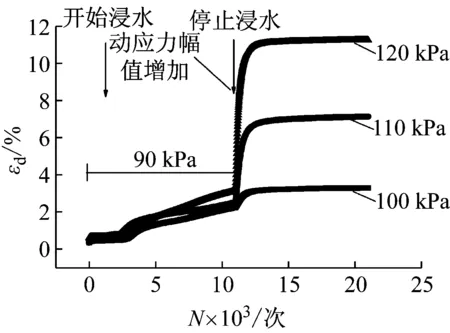
图6 情况三不同动应力幅值下应变- 振次关系曲线

Fig.6 Strain vibration relationship curves under different dynamic stress amplitudes in situation 3

图7 情况一浸水量曲线

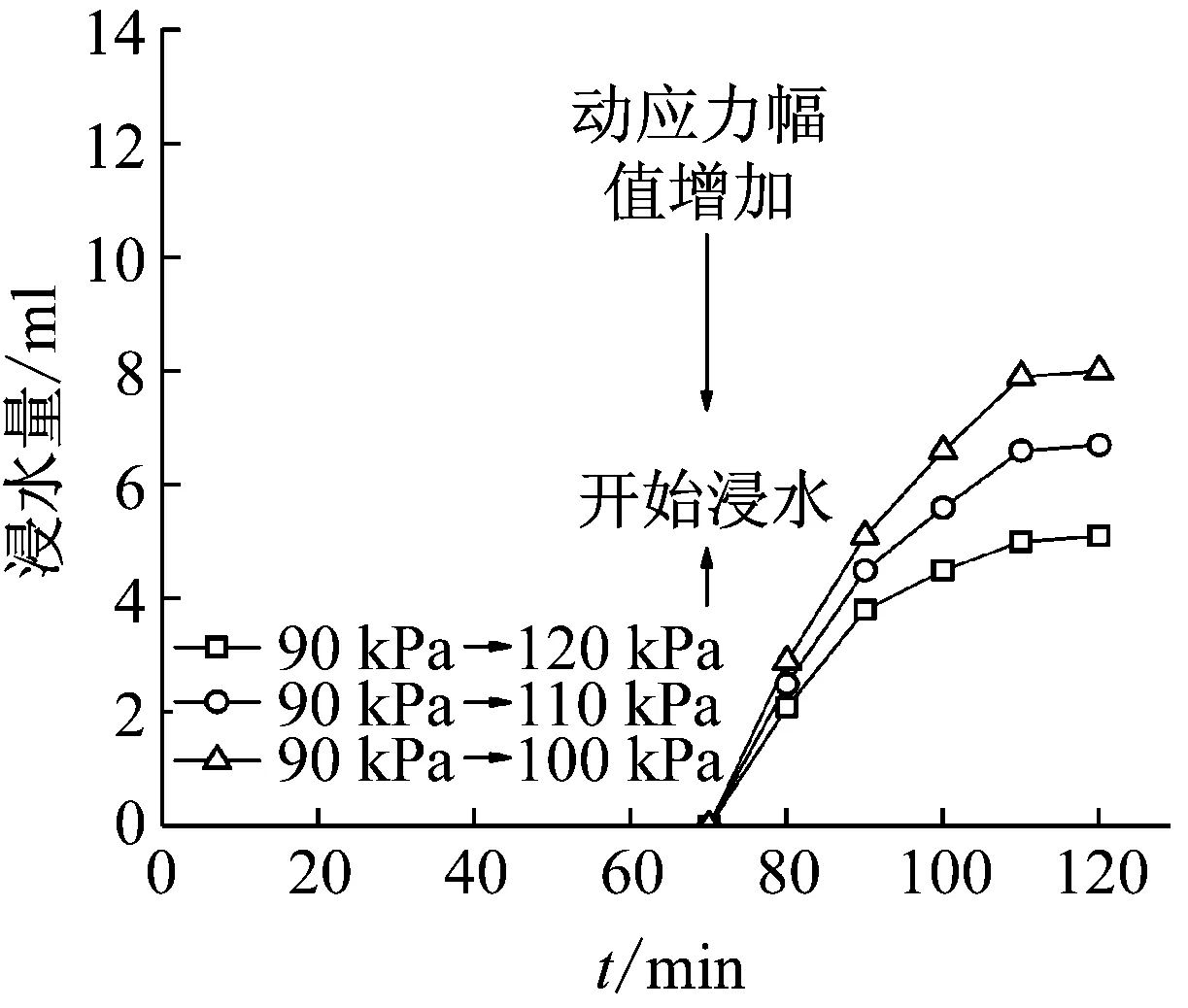
图8 情况二浸水量曲线

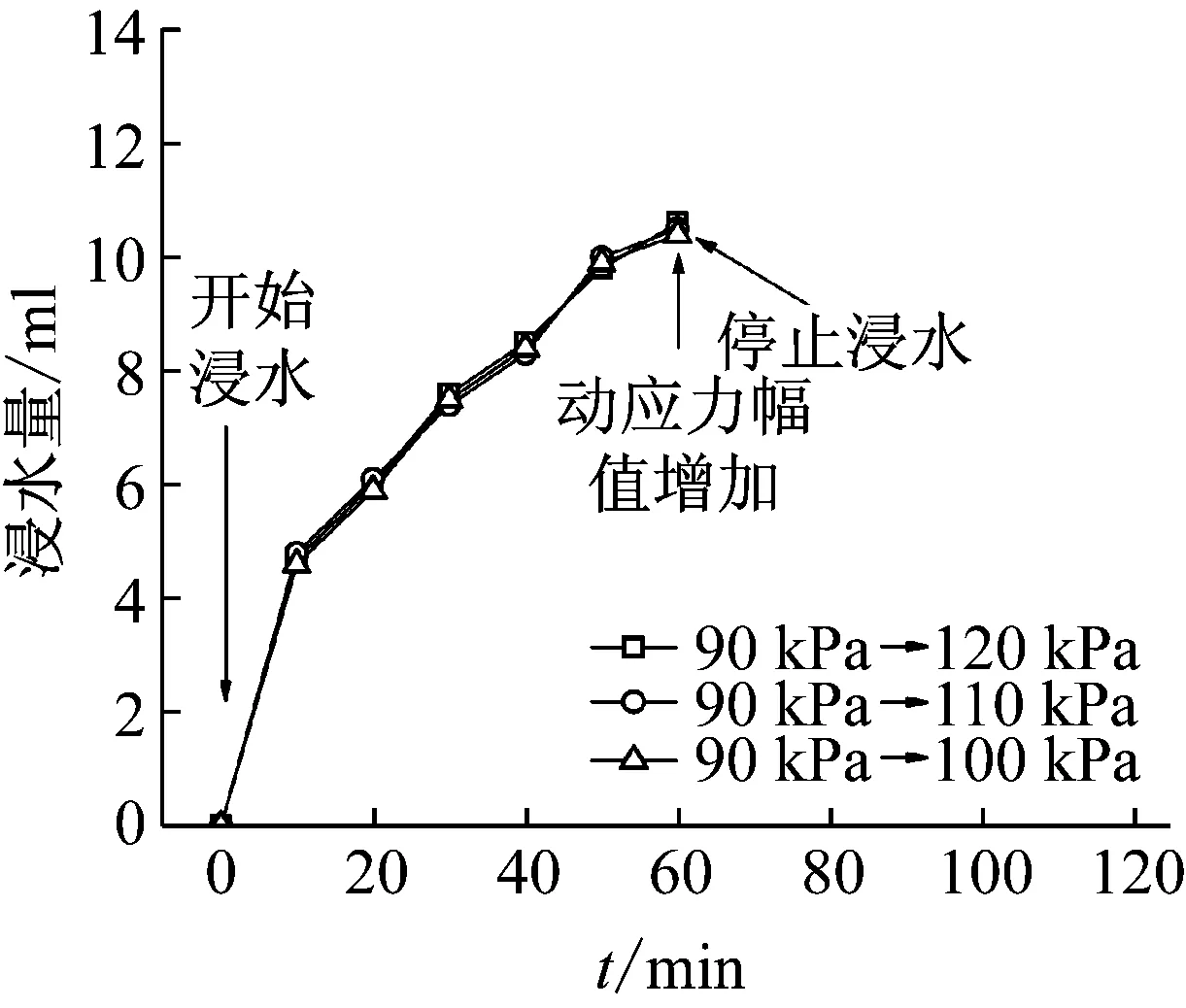
图9 情况浸水量曲线

从图中可以看出，情况一的浸水量随时间先增加，在动应力幅值增加后开始出现转折点趋于稳定，且动应力幅值越大浸水量越小，120 kPa对应的浸水量是最小的，这是因为随着动应力幅值的增加，土体孔隙率逐渐减小，渗透性也随之降低，情况二在动应力幅值增加后开始浸水，浸水量呈现上升趋势，上升趋势较情况一略大，因为土体在前期未经历浸水过程，土体的孔隙率较情况一更大，最终因孔率降低浸水量趋于稳定，同样是动应力幅值越大浸水量越小；情况三在后期停止浸水，只有前期在90 kPa动应力作用下的浸水量曲线，与情况一的前半部分基本一致。

本文取动应力幅值为120 kPa下N=1 000、N=6 000、N=11 000、N=16 000、N=21 000时的滞回圈绘制出三种情况下的滞回关系曲线，横轴为轴向应变，纵轴为动应力幅值，通过分析各滞回曲线图10～图12所示。

可以看出滞回圈局整体向右平移，说明随动应力幅值和振次的变化变形在增加，在第一种情况下N=11 000对应的滞回圈较N=16 000对应的滞回圈有一个很大的平移，因为在N=11 000时动应力幅值增加，说明在动应力幅值增加后应变增加很快，而N=16 000对应的滞回圈较N=21 000对应的滞回圈平移距离很小说明在这个阶段应变已达到稳定状态；第二种情况下N=1 000，N=6 000，N=11 000对应的滞回圈平移量很小，说明在前期不浸水的情况下应变较小，N=11 000，N=16 000，N=21 000对应的滞回圈开始产生较大平移，因为在N=11 000时开始浸水并增加动应力幅值，说明在动应力与湿化共同作用下应变增长显著；第三种情况与第一种情况相似，只是应变相对较小。

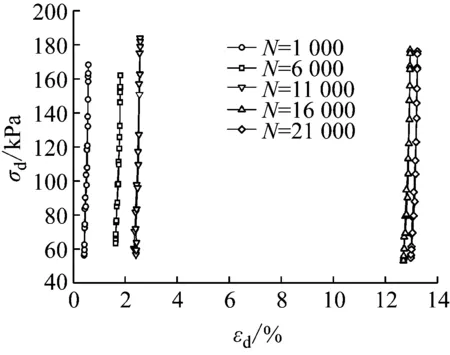
图10 情况一滞回关系曲线(120 kPa)

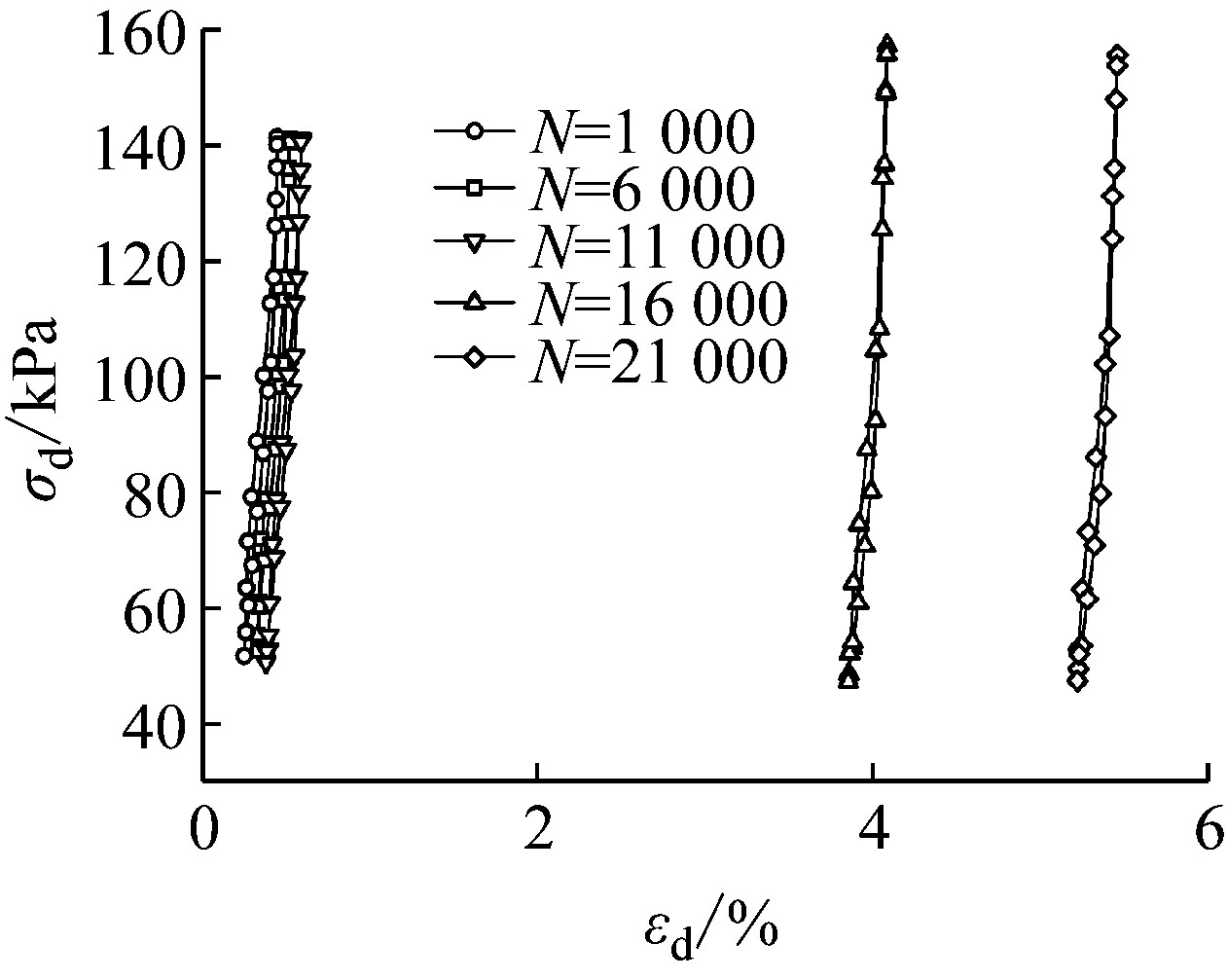
图11 情况二滞回关系曲线(120 kPa)

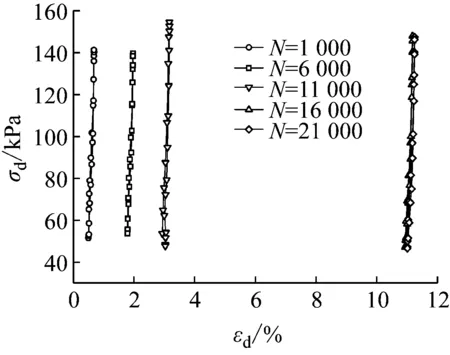
图12 情况三滞回关系曲线(120 kPa)

土体在不同浸水过程下会产生不同程度的软化现象，软化指数能够很好的反应土体在循环荷载下的应变及软化情况，Idriss等[22]、周健等[23]、龙尧等[24]Matasovic等[25]均对软化指数进行了相关研究，蔡袁强等[26]依据Idriss对软化指数的定义，重新定义了软化指数如下

(2)

式中：qN,max，qN,min分别为第N次循环偏应力的最大值和最小值；εaN,max，εaN,min分别为第N次循环轴向应变的大值和最小值；q1,max，q1,min分别为第1次循环偏应力的最大值和最小值；εa1,max，εa1,min分别为第1次循环轴应变的最大值和最小值。

本文依据此公式绘制出三种情况下的软化指数与振次关系曲线如图13～图15所示。

从图中可以看出，情况一和情况三在开始浸水后软化指数逐渐减小在动应力幅值增加后软化指数很快趋于稳定，并且后期动应力幅值大的软化指数相对较高，情况二在浸水前软化指数有一个小的下降趋势基本无太大变化，浸水后软化指数显著下降，同样是后期动应力幅值大的软化指数相对较高，因此长期湿化作用会使土体率先达到稳定状态。

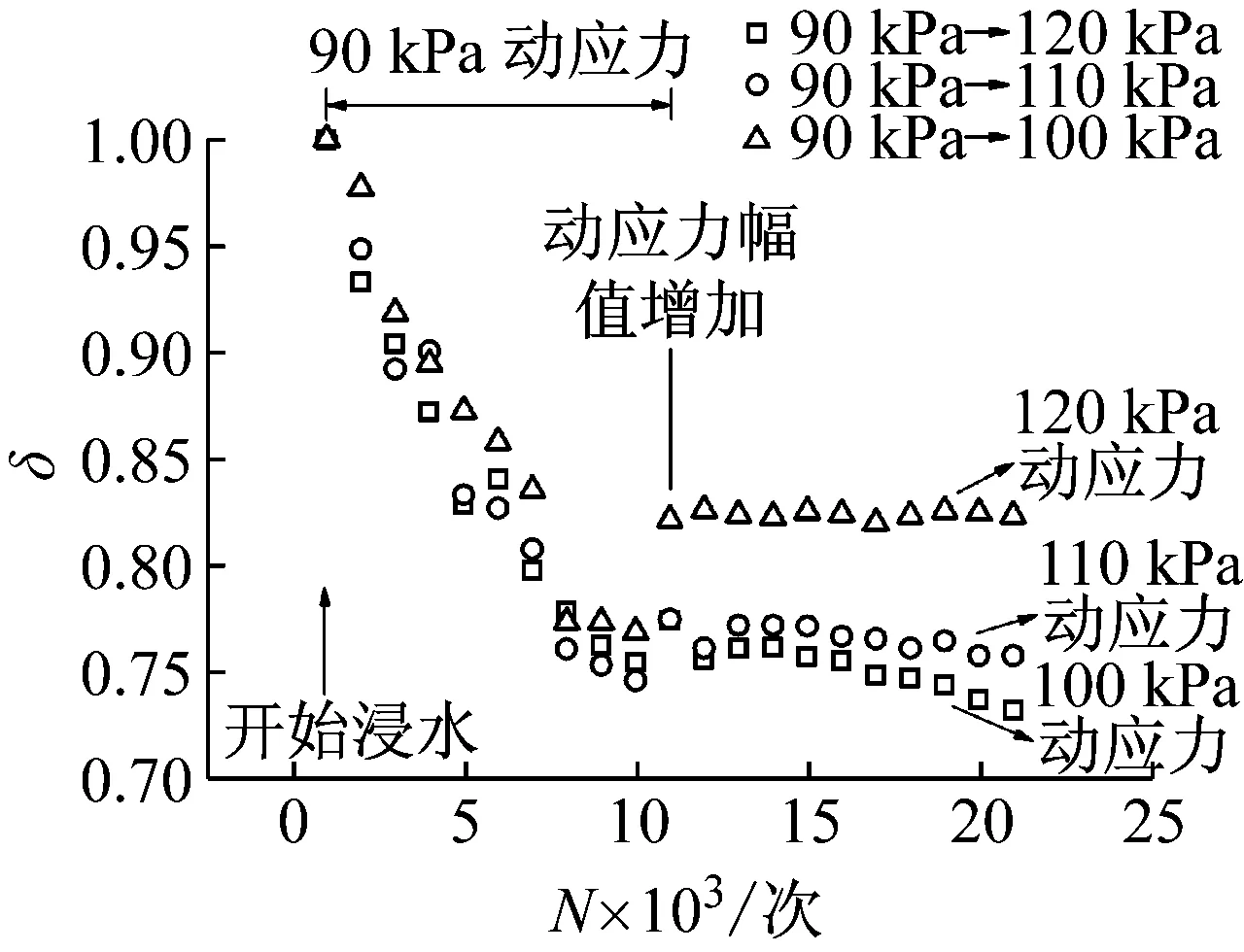
图13 情况一软化指数-振次关系曲线

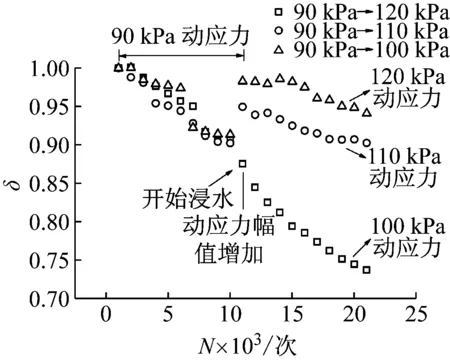
图14 情况二软化指数-振次关系曲线

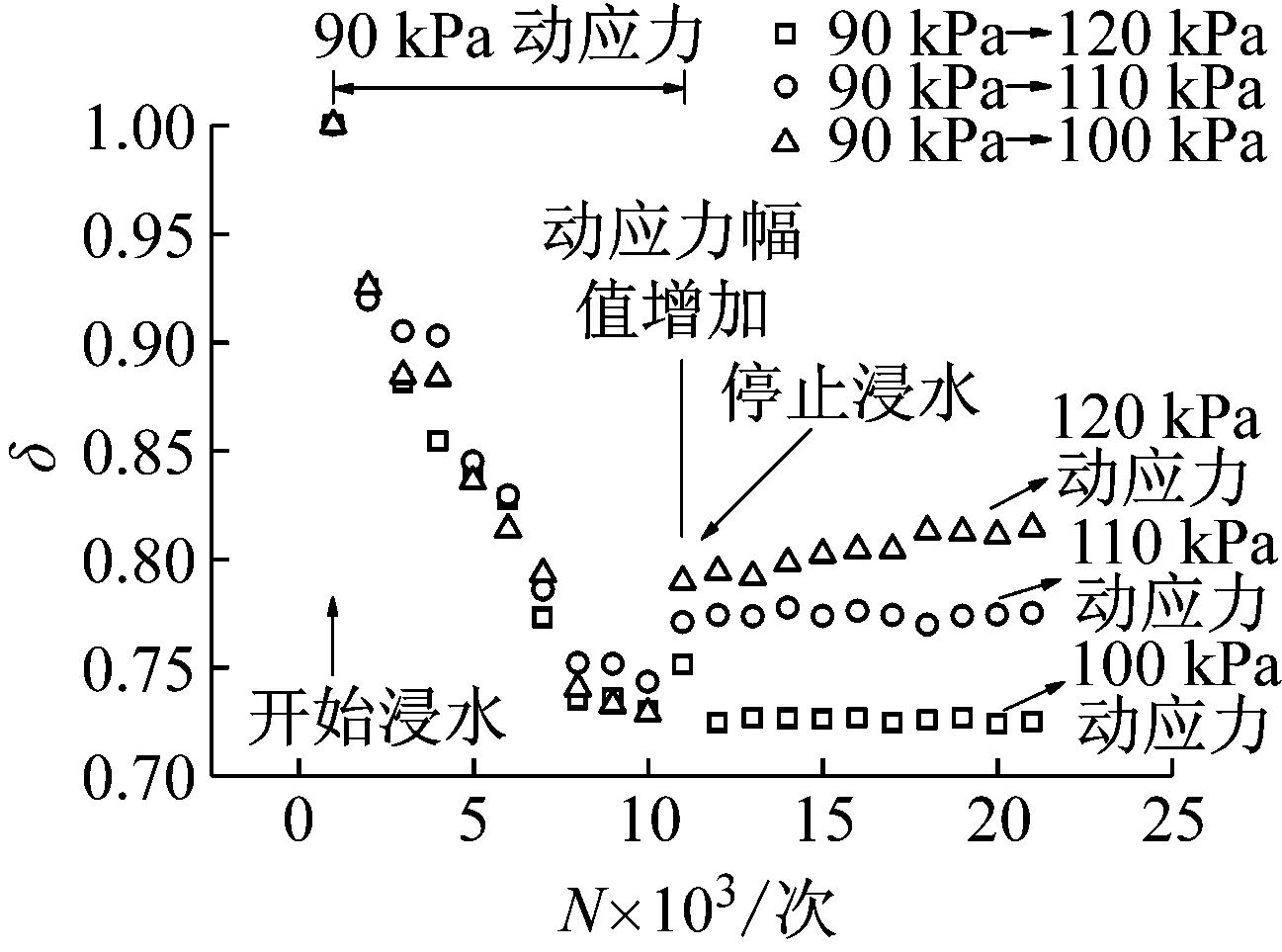
图15 情况三软化指数-振次关系曲线

为了更直观动应力幅值增加后的应变较之前的改变量，本文将不同情况下轴重增加后阶段的应变减去动力加载阶段的应变绘制出应变差值曲线，该曲线能更好的反映不同情况下动应力幅值增加前后的应变增量。

定义第一种情况下动力稳定阶段产生的应变为εⅠ浸，最终稳定后的应变为εⅠs浸，动应力幅值增加阶段产生的应变为εⅡ浸，最终稳定后的应变为εⅡs浸；第二种情况下动力稳定阶段产生的应变为εⅠ干，最终稳定后的应变为εⅠs干，动应力幅值增加阶段产生的应变为εⅡ浸，最终稳定后的应变为εⅡs浸；第三种情况下动力稳定阶段产生的应变为εⅠ浸，其最终稳定的应变为εⅠs浸，动应力幅值增加阶段产生的应变为εⅡ干，最终稳定后的应变为εⅡs干。应变差值曲线如图16～图18所示。

从图16～图18可以看出：在增加后的动应力幅值为100 kPa时，第一种情况和第三种情况的差值曲线在10 000周次内基本达到稳定，且第一种情况的差值曲线高于第三种情况的差值曲线，第二种情况的差值曲线则一直成上升趋势，开始时差值曲线最低，随后接连超越第三种情况的差值曲线逼近第一种情况的差值曲线，说明在增加后的动应力较小时第二种情况产生的应变和第一种相近要引起重视，而在增加后的动应力幅值为110 kPa和120 kPa时，情况一高于情况二和情况三，因此当增加后的动应力幅值较大时第一种情况对应的应变最大。

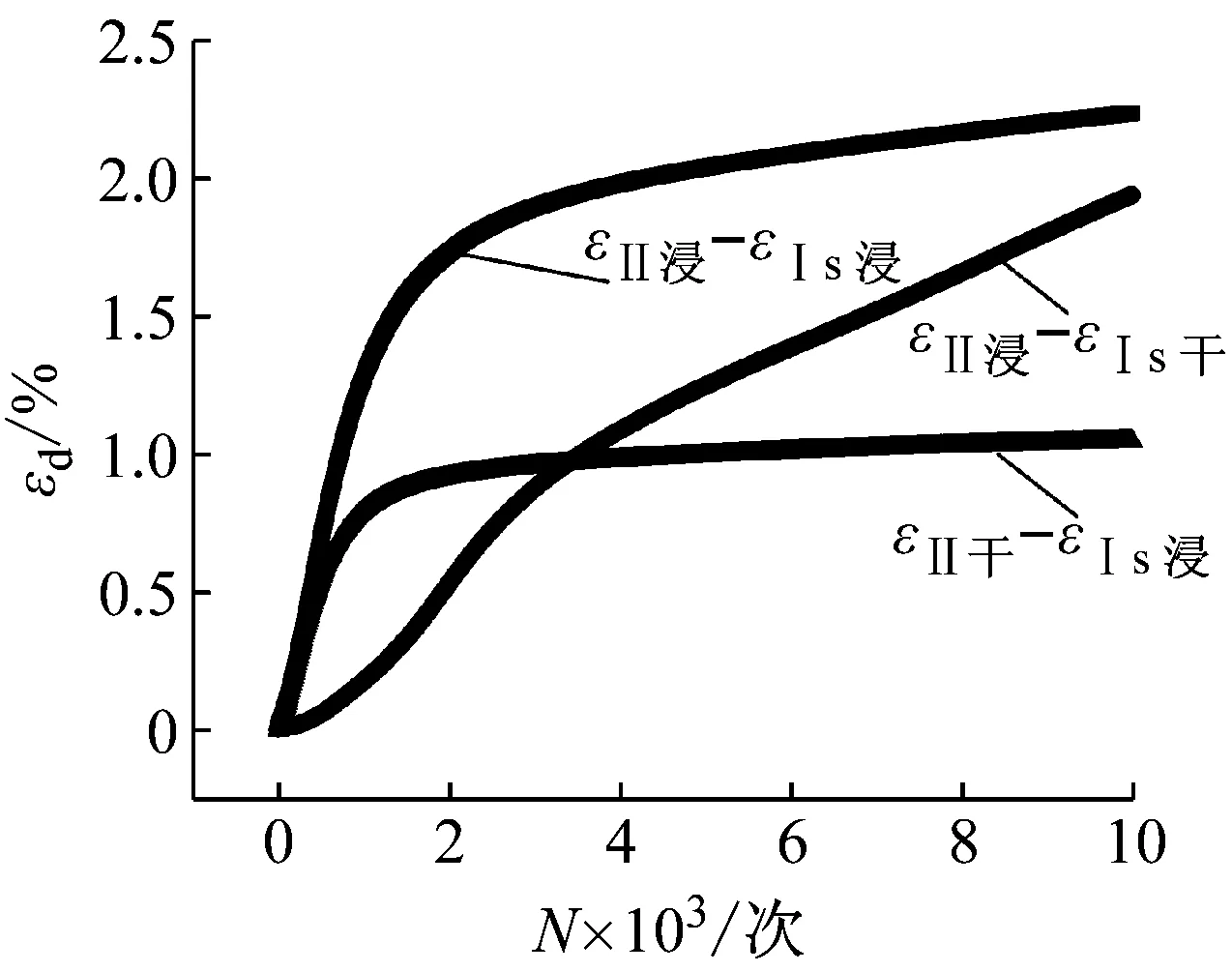
图16 不同情况下的应变差值 曲线(100 kPa)

图17 不同情况下的应变差值 曲线(110 kPa)

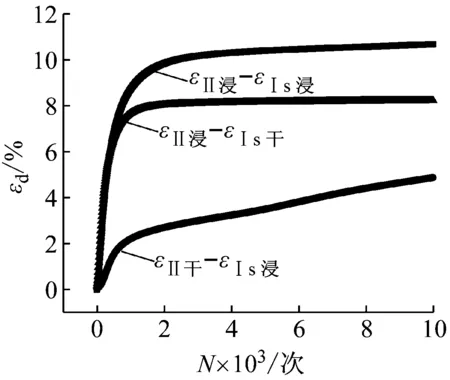
图18 不同情况下的应变差值 曲线(120 kPa)

图19为三种情况下不同增加后的动应力幅值与最终稳定的湿化变形量关系曲线，可以看出在情况一的浸水过程下产生最大的应变，情况一与情况三的最终稳定的应变变化规律相似，在100 kPa和120 kPa时两种情况的最终稳定应变相差约2%，110 kPa时相差约3%，这部分差值是由湿化作用产生，因此湿化对于土体的应变量影响十分显著，在增加后的动应力幅值为100 kPa时，情况二与情况一的应变相近。因此对于既有线路扩能改造，基床的浸水过程属于情况一的，要特别重视其湿化变形，对于扩能改造后为轴重荷载约为100 kPa的既有线路，在情况一和情况二两种浸水过程下基床的湿化变形是相近的。

图19 不同动应力幅值下的应变量

3 结 论

(1)第一种和第三种情况下土体应变的变化规律相似，但第一种情况的应变更大，在100 kPa和120 kPa作用下两种情况的最终稳定应变相差约2%，110 kPa作用下最终稳定应变相差约3%，第二种情况下土体应变趋势较大，并未出现稳定趋势。综上表明浸水路基在扩能改造后变形较大稳定较快，未浸水路基扩能改造后在浸水作用下基床湿化变形趋势较大，不易达到稳定状态。

(2)由于动应力幅值的增加会降低土体孔隙率，故浸水量随动应力幅值的增加而减小。

(3)第一种和第三种情况下土体的滞回圈间距先增大，在动应力幅值增加后逐渐减小直至近乎重合，第二种情况下土体的滞回圈间距开始较小近乎重合，在开始浸水且动应力幅值增加后滞回圈间距逐步增大。

(4)在第二种情况下土体的软化指数下降较快，土体软化趋势较大，第一种和第三种情况下土体的软化指数在动应力幅值增加后很快趋于稳定，软化趋势不明显。

(5)在相同的浸水过程下，应变随动应力幅值的增加而增加，列车荷载超过120 kPa时产生的应变较大，应变将成为路基扩能改造的控制因素。对于扩能改造后承受列车荷载约为100 kPa的基床，在前期未浸水后期浸水和前后期均浸水两种情况下最大湿化变形相近。

分析了不同浸水过程下的重载铁路基床动力湿化特性，试验过程更加符合实际情况，并通过试验发现，在大轴重的既有线路扩能改造建设中，长期浸水基床的湿化变形最大，可以为不同地区重载铁路的扩能改造提供有价值的参考。