基于微纳耦合光纤传感器的模态声发射源线性定位研究

付文成, 刘懿莹, 王霖洁, 李凤梅

(西安交通大学 电气工程学院， 西安 710049)

声发射技术被广泛地应用于航空航天、土木工程、金属加工、电力设备故障诊断等方面，其主要目的之一是对结构、工件的损伤位置和损伤类型进行判断[1-5]。时差定位是声源定位中使用最多的方法，其前提条件是材料中传播的声速已知。在主动超声检测中，根据所用声波种类能够轻易获得声速。但对于被动声发射检测而言，由于材料结构，声源性质，声源与传感器距离等因素，使传感器接收的声波成分复杂，尤其是在板状构件中传播的声发射波是一种频散波，这种波不仅不同成分传播速度不同，还与信号频率相关。如果不加区分的利用同一声速求时差，会产生很大的定位误差[6-7]。模态声发射技术在传统声发射技术的基础上，充分考虑了声发射波在介质中不同传播模态之间的差异性(传播速度、能量、频率以及衰减特性)，能够从声发射信号中提取更多有用信息[8-9]。通过信号处理手段识别模态之间的差异能够使损伤位置判断更精确，同时减少传感器的数量。

目前，大部分模态声发射定位研究中，常常使用较为成熟的压电换能器作为传感器[10-12]。但压电换能器易受电磁干扰，不能在高温高压等恶劣环境下工作。微纳耦合光纤传感器(Micro-Fiber Coupled Sensor，MFCS)由于其在满足灵敏度要求的同时，具有良好的抗电磁干扰能力，并且制作简单，解调成本低等优点，受到国内外学者的关注。目前，已报道文献主要是对微纳耦合光纤的声发射传感特性的研究[13-15]，并初步研究了其在时差法声源定位中的应用[16-17]。然而在已有的研究中，还未有将该传感器应用于模态声发射的检测和定位中。

本文研究了微纳耦合光纤传感器在S0/A0峰值定位方法和A0/A0阈值定位方法中的应用，分别研究了影响两种方法定位结果的因素，并对比分析了两种定位方法的优缺点。

1 声发射信号模态分析及实验平台

1.1 声发射信号模态分析

根据模态声发射理论，声发射波在固体中主要以Lamb波的形式传播，Lamb波是一种在厚度与激励声波波长为相同数量级的薄板波导中由于薄板上下边界多次反射致使纵波和横波多次耦合而形成的特殊形式的应力波。Lamb波主要包括对称模态(S0,S1,S2……)和反对称模态(A0,A1,A2……)两种传播模态[18]。通常情况下，两个模态的能量主要集中在S0与A0两个最基本的模态。其中，S0模态的传播速度较快，特点是频率较高、能量较小并且容易淹没在噪声中，它的传播速度和材料性质有关，特别在各向异性材料中，不同的传播方向其传播速度也不同；A0模态的传播速度相对较慢，特点是频率较低、具有明显的频散特性，并且能量远高于S0模态，其传播速度与材料的厚度有关[19]。对于不同的平板参数，S0和A0模态具有不同的频散效应，其频散曲线可通过求解Rayleigh-Lamb方程得到。本文选用具有高抗疲劳强度的各向同性防锈铝板5052，其各项参数列于表 1，将其代入Rayleigh-Lamb方程，可求解得到该材料上各模态传播速度的频散曲线，如图1。

表1 5052铝板材料性能参数

如图 1所示，两种模态的频散速度分布不同，速度变化趋势也不同，而且一个模态的不同频率成分具有不同的传播速度。当频率在0～300 kHz时，A0模态的群速度随着频率增加明显增大，而S0模态的群速度几乎不变，同时S0模态的群速度远大于A0模态。当频率在300 kHz～1 MHz，A0模态的群速度几乎不变，而S0模态的群速度随着频率增加明显下降。说明在0～300 kHz频率段内，A0模态频散效果明显，S0模态频散效果不明显；300 kHz～1 MHz频率段内，A0模态频散效果不明显，S0模态频散效果明显。

图1 实验铝板上S0、A0模态的群速度频散曲线

本文研究了0～300 kHz频率范围内S0，A0的模态特性，分别利用不同模态间的群速度差(S0/A0)和同一模态下的频散特性(A0/A0)进行定位研究。同时对这两种定位方法的定位结果进行了详细的对比分析和综合评估。

1.2 微纳耦合光纤传感器

微纳耦合光纤声发射传感器是由光纤耦合器发展而来。光纤耦合器作为一种常用的光学无源器件，在光学系统中发挥着极其重要的作用。通常，光纤耦合器被用在光分路及光合路上，随着光纤技术的发展，经过特殊设计的耦合器还能够用于偏振分光、光波滤波及光的波分复用。光纤耦合器主要通过腐蚀、抛磨或是熔融拉锥三种工艺制作而成，通过加工两根分立光纤融合成一体，其结构及工作原理如图2所示。

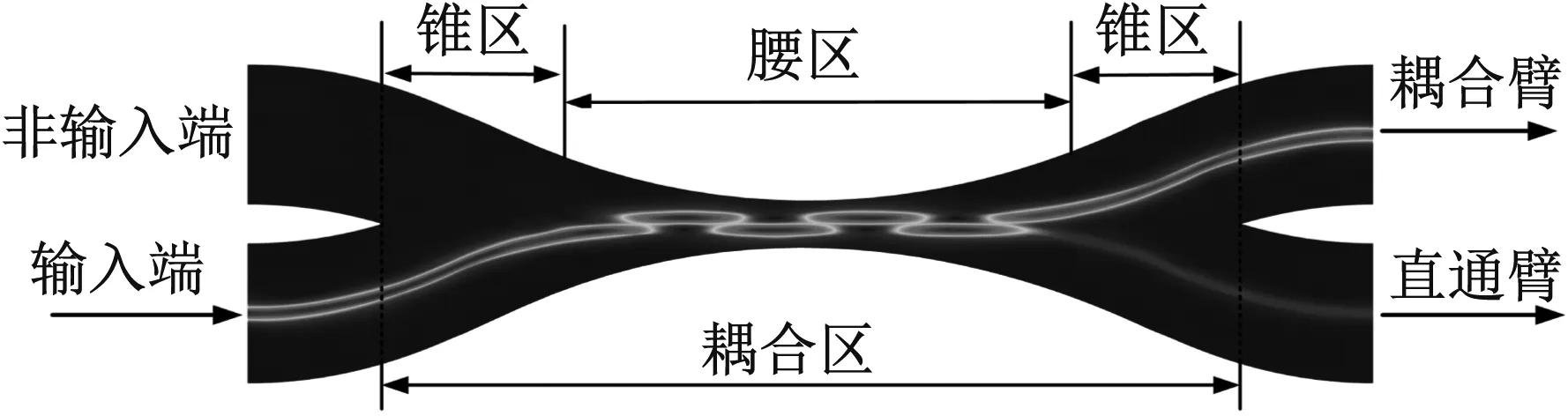
图2 光纤耦合器示意图

将一束光通入微纳耦合光纤传感器任一输入端，在锥区光开始耦合到另一根光纤中，在细腰区两根光纤中的光能量不断交换，直至以一定分光比从两端输出。耦合光输出与耦合器的耦合区(锥区和腰区)尺寸、两根光纤的纤芯距离以及光纤的材质特性有关。输出光功率与耦合器结构尺寸存在定量关系

ΔP1=Δl·sin (2Cl)·

(1)

式中：V为归一化频率，n为微纳耦合光纤纤芯折射率，rw为腰区的半径，λ为光波波长，k为传感器截面的横纵比，pij和υ分别为弹光张量和泊松比，Δl为传感器x轴向的形变量。式(1)中，在微纳耦合光纤传感器成形后，除了Δl，其他参数均由材料本身决定，因此输出光功率变化主要与轴向方向形变量有关。

振动、超声会导致耦合器结构尺寸的微小变化，从而引起输出光功率的变化。基于此可将耦合器改进成为微纳耦合光纤传感器，以实现对振动、超声等物理量的测量。

本研究使用的传感器是由实验室基于熔融拉锥工艺制作的微纳耦合光纤传感器。

1.3 实验平台

为了研究基于微纳耦合光纤传感器的模态声发射源定位技术，搭建了实验平台。如图3 所示，为了减少波反射，使用大铝板(1.0 m × 0.8 m × 2.0 mm)作为实验载体,将微纳耦合光纤通过声波耦合剂粘贴于铝板上，本文中使用的声波耦合剂均为UV胶；窄带激光光源(康冠光电，1 310 nm DBFLIGHTSOURCE)发出1.0 mW功率的光通过连接器连接至微纳耦合光纤传感器的其中一输入端，光经过传感器被一分为二分别输出至光电转换模块(THORLABS, DET01CFC)，转换成的电信号V1和V2接入低噪声前置放大器A(V1-V2)(Stanford,SR560)进行差分放大，最后由示波器采集并传输至电脑进行处理。声发射源垂直于传感器方向，以5 cm为步长逐渐增加至80 cm，由铅笔芯断裂法产生。

图3 基于微纳耦合光纤传感器的模态声发射源线性 定位实验平台

Fig.3 Experimental platform of modal acoustic emission source linear location based on micro-fiber coupled sensor

2 基于单微纳耦合光纤传感器的声发射源线性定位方法

2.1 基于S0/A0方法的声发射源线性定位

假设，传感器所测信号中既包含S0模态又包含A0模态，在某一频率下S0模态传播速度和到达时间分别为vS0、tS0，A0模态的传播速度和到达时间分别为vA0、tA0，则声源与传感器的距离d可由下式计算

(2)

图4为定位方法流程图。首先，提取所测超声信号，对其进行带通滤波处理，带宽为20～400 kHz；对滤波后信号进行Gabor变换，获取信号的时频分布图；根据S0、A0模态的频散特点，S0能量较小，在低频域没有明显的频散现象，其时频图中的各频率分量几乎同时到达，而A0能量较大，在低频域频散明显，其时频图中低频分量相对于高频分量到达时间明显滞后，由此可实现S0、A0两个模态的识别。接着，选取信号S0模态能量峰值对应的频率作为计算频率，选取的算法为：① 首先设定一个噪声阈值，时域信号中判定S0到达的大概时刻；② 在时频图中以该时刻为基础向周围搜索，得到信号能量最大值；③ 将该最大值对应频率作为计算频率，绘制该频率下Gabor系数随时间的变化图。然后，分别设定S0模态判定阈值和A0模态判定阈值，并将越过阈值的第一个波峰对应时刻作为该模态下的到达时间；根据式图 1可得到两个模态的该频率分量的传播速度；最后代入式(2)中计算得到声源距离。

图4 S0/A0定位方法流程图

图5给出了声源距传感器30 cm处，典型信号的Gabor变换图及其计算频率下的Gabor系数分布， Gabor系数表征能量大小，横坐标为时间，纵坐标为频率。Gabor系数分布反映了信号整体的频散效果，也反映出信号任一频率分量随时间变化曲线。

如图5(a)所示，信号在400 μs左右出现频率为130～230 kHz的波，在420 μs后出现集中于20～300 kHz的波。根据S0模态传播速度快，能量低，频散效果不明显等特点，可确定图5(a)中最先出现的波为S0模态；而A0模态传播速度慢，能量大，频散效果明显，可确定图5(a)中随后出现的波为A0模态。接下来在400 μs时刻附近搜索S0模态中能量最大值及其所对应的频率，得到计算频率f=209 kHz。绘制f=209 kHz下的Gabor系数分布图，由于S0模态和A0模态两者能量相差较大，因此对Gabor系数取对数表示(本文中其余图均如此)。

(a) 传感器所测d=30 cm处声发射信号Gabor变换

(b) 209 kHz对应的Gabor系数分布

为了判定两个模态的到达时间，设置f=209 kHz下前300 μs(噪声)的Gabor系数能量最大值的2倍作为S0模态判定阈值，同时设置f=209 kHz下Gabor系数能量最大值的5%作为A0模态判定阈值，越过这两个阈值的第一个波峰时刻作为对应模态的到达时间。

由图5(b) 中可得出S0模态的到达时间tS0和A0模态的到达时间tA0分别为393 μs和447 μs，又根据图 1得到两个模态在f=209 kHz下的传播速度分别为：vS0=5 310.5 m/s，vA0=2 792.8 m/s；代入式(2)可计算得到声源距离d′=31.8 cm，相对于实际距离d=30.0 cm，绝对误差为1.8 cm，相对误差为6%，表明了利用微纳耦合光纤传感器，基于S0/A0方法对模态声发射源线性定位是有效可行的。

2.2 基于A0/A0方法的声发射源线性定位

如果检测到的A0模态频带较宽，频散效果足够好，则可由A0模态在低频段(0～300 kHz)频散曲线可知，不同频率分量的传播速度差异较大。理想情况下，可任意选取A0模态下两个不同的频率分量进行计算：先得到两个频率分量的到达时间差，再结合两个频率分量的传播速度，可以计算得到声源的距离。设任意选取的两个频率分量分别为f1，f2，其对应的传播速度为vA01，vA02，到达时间分别为tA01，tA02，最后声源的距离可以由式(3)计算

(3)

图6为A0/A0定位方法的流程图。首先，提取所测超声信号，对其进行带通滤波处理，提取有用信息，选取带宽为20～400 kHz；对滤波后信号进行Gabor变换，获取信号的时频分布图；根据A0模态能量大，在低频域内的频散效果明显的特点，容易识别出A0模态；频率分量的选取较为灵活，一般选取频散效果连续、能量分布均匀处的两个点进行计算；为了判定A0模态不同分量的到达时间，基于Gabor变换图绘制阈值等值线图，阈值大小按信号最大能量的百分数进行划定，这样两个频率分量与阈值等值线的交点所对应的时刻即作为该分量的到达时间；再根据图 1得到A0模态两个分量的传播速度；最后代入式(3)计算得到声源距离。

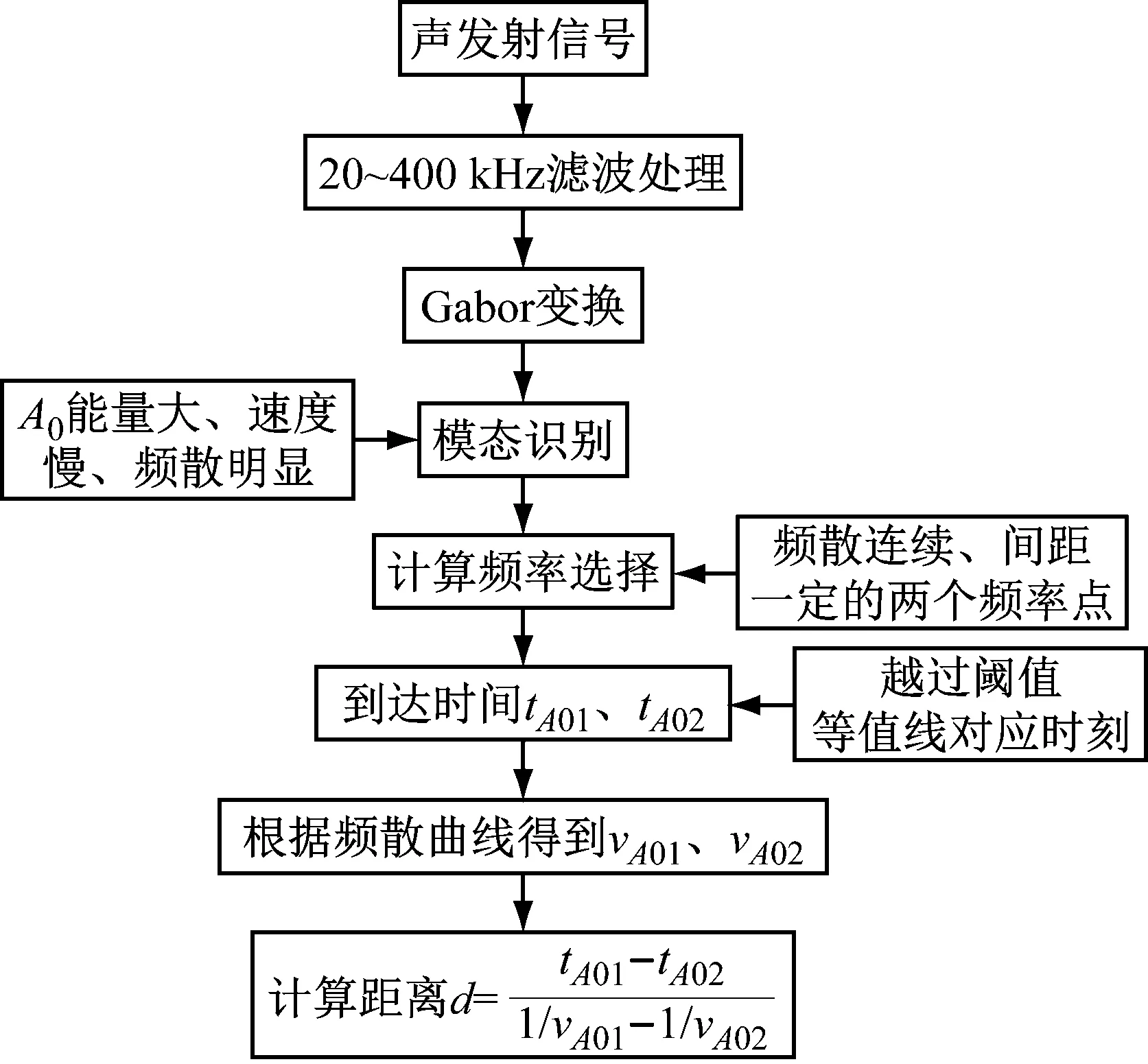
图6 A0/A0定位方法流程图

这里需要指出，A0模态在传播过程中会出现边缘反射、波的叠加及模态转换等现象，导致Gabor分布中A0模态某些频率分量的峰值到达时间滞后，若仍采用越过设定阈值的第一个波峰作为到达时间，则会导致某些频率分量到达时间的误判断，从而引起较大的定位误差。因此，采用A0模态不同频率分量进行定位时，两个频率分量的到达时间应该选取与阈值等值线交点对应的时刻。

以图 5(a)为例，通过3.1已经识别出A0模态，接下来，设定适当阈值并绘制其等值线图，本例选取信号Gabor变换最大能量的5.74%作为阈值，绘制该等值线图。如图7所示，在等值线图中任意选取两个间隔一定的频率点作为计算频率，本例选取f1=150 kHz，f2=50 kHz作为计算频率；这两个计算频率分别交阈值等值线于a，b两点，由图中可以读出这两点的坐标分别为：a(458.1 μs，150 kHz)、b(511.1 μs，50 kHz)。因此，150 kHz分量的到达时间为tA01=458.1 μs，50 kHz分量的到达时间为tA02=511.1 μs。查询图1的频散曲线图可得两个分量的传播速度：vA01=2 582.0 m/s(150 kHz)，vA02=1 775.1 m/s(50 kHz)。代入式(3)计算可得到声源距离为d′=30.1 cm，与实际距离d=30.0 cm仅相差0.1 cm，证明本方法是精确有效的。

图7 图5(a)对应的阈值等值线图

3 S0/A0、A0/A0两种定位方法的定位结果分析及综合评价

3.1 S0/A0方法定位结果分析

实验表明，在使用S0/A0方法定位时，Gabor变化时间分辨率的差异会对定位结果引起不同程度的影响。为了定性分析Gabor变换时间分辨率对定位结果的影响，采用不同的时间分辨率对同一信号进行对比分析。同时，为了更好的评估S0/A0定位方法，从定位精度、定位重复性以及误差分析对其定位结果进行了详细讨论。

3.1.1 Gabor变换时间分辨率对模态识别准确度的影响

在本文中，分别采用不同时间分辨率的Gabor变换对图5的信号进行对比分析，并详细研究其定位结果。分析结果如图8所示，图8(a)、(c)、(e)分别为高、中、低时间分辨率下同一信号的Gabor变换。图8(b)、(d)、(f)分别为图8(a)、(c)、(e)对应的S0模态能量最大值对应频率及在该频率下的Gabor系数分布。

分析图8(a)、(c)、(e)可以看到，时间分辨率对信号Gabor变换的特征具有很大影响，识别出的S0模态最大能量位置也不一致，时间分辨率越高，变换的信号显示约“瘦高”，此时S0模态更为清楚；时间分辨率越低，变换信号显得越“矮胖”，S0模态与A0模态混淆，难以识别；在图8(b)、(d)、(f)中，对比分析S0模态能量最大值对应频率及在该频率下的Gabor系数分布，可以看到在中高时间分辨率下，S0模态仍能较好地被识别，且时间分辨率越高，信号的峰值数量越多；而在低时间分辨率下和A0模态相融，没有形成波峰，故没法判定S0模态的到达时间，导致定位失败。

(a) 高时间分辨率(b) 高时间分辨率

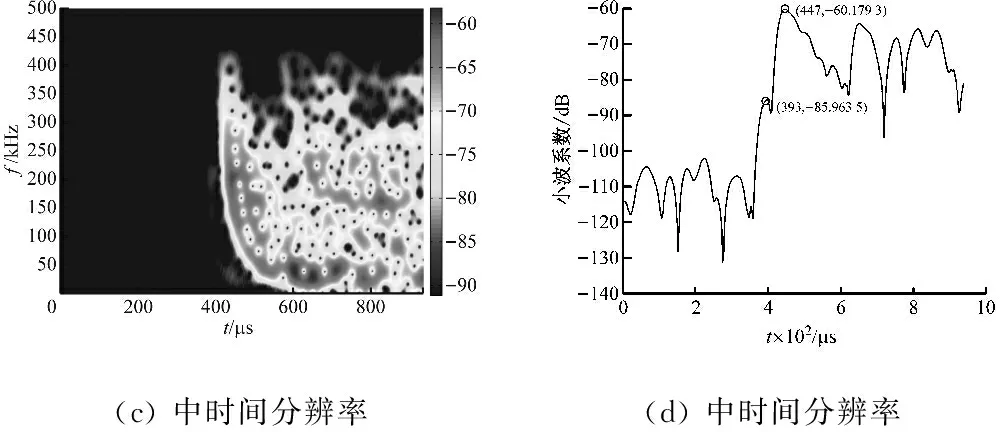
(c) 中时间分辨率(d) 中时间分辨率

(e) 低时间分辨率(f) 低时间分辨率

图8 不同时间分辨率对信号Gabor分布及其定位过程的影响

Fig.8 Influence of time resolution for the Gabor distribution and locating process

事实上，本文的S0/A0定位方法中到达时间的判定是采用的峰值法，而提高时间分辨率能够更清楚地区分不同模态的峰值以至于不混淆，因此能够提高模态识别准确度及定位结果，故利用S0/A0定位方法定位时应设定一个较高的时间分辨率。

3.1.2S0/A0定位结果分析

(1) 定位精度及范围

实验探索了微纳耦合光纤的定位范围，分别测试了声源距传感器为5 cm、10 cm、15 cm、……、40 cm的定位结果。定位结果列于表2和图9。

表2给出了传感器S0/A0定位方法的实验结果，综合各个点定位的绝对误差来看，微纳耦合光纤的定位绝对误差为0.4～2.3 cm，具有较好的定位准确度；而从相对误差来看，利用此方法进行5 cm以内的近距离定位不具有优势，这是因为声发射源过近，其S0,A0模态在近距离传播中并不能很好的分开，这样两者的模态识别难度大，从而导致较大的误差，因此基于微纳耦合光纤S0/A0定位方法定位范围需大于5 cm。图9更为直观地显示了定位结果随实际距离的变化关系。

表2 基于微纳耦合光纤S0/A0定位方法的实验结果

图9 基于微纳耦合光纤S0/A0定位方法的实验结果

由图9可以看出，定位误差随着实际距离的增加而增大，当测试距离大于40 cm后，由于Lamb波随传播距离增大而衰减导致S0模态能量太小，难以捕捉，这也意味着基于微纳耦合光纤的S0/A0定位方法的范围主要取决于传感器对S0模态的灵敏度和声源能量的大小。综上所述，目前基于微纳耦合光纤S0/A0定位方法的适用范围为5～40 cm。

(2) 定位重复性

为了验证微纳耦合光纤定位的重复性和可靠性，利用铅笔芯断裂法分别在距离传感器d=15 cm和d=25 cm处重复测试15次，对15次测试信号进行定位计算，其结果列于表3。

表3 d=15 cm和d=25 cm处15次重复定位结果

定位结果表明，微纳耦合光纤在15 cm处和25 cm处均具有较好的定位结果。在15 cm处15次重复定位平均距离为14.16 cm，绝对误差0.74 cm，在25 cm处15次重复定位平均距离为26.24 cm，绝对误差1.24 cm，考虑传感器自身长4.4 cm，因此这两个位置的定位误差是可以接受的。

重复性可以通过15次测量结果的标准偏差表征，数据的标准偏差越小表明数据重复性越好，定位越稳定。由表3可知，微纳耦合光纤在15 cm处定位的绝对标准差为1.06 cm，在25 cm处定位的绝对标准差为1.14 cm，表明了基于微纳耦合光纤的S0/A0定位方法具有较好的重复性。

(3) 误差分析

基于微纳耦合光纤的S0/A0方法的定位误差主要来自于三个方面：①S0模态识别及其到达时间的判断；② 传感器的灵敏度及声源能量大小；③S0,A0模态群速度频散曲线理论与实际的偏差。本方法的难点在于S0的识别，S0模态由于能量小往往低于信号触发的阈值，仅从信号时域图很难辨别，只有通过Gabor分布降低阈值才能看到，这也是Gabor变换的一大优势。由图 1可知在f=100 kHz时，S0模态传播速度为5 414 m/s，而A0传播速度为2 301 m/s，S0模态的传播速度约为A0模态的两倍，故Gabor分布中S0可能发生反射叠加，其反射波仍在A0模态到达时间之前，这样会导致S0模态识别的混淆，引入误差；信号的信噪比是另一个导致误差的因素，S0模态由于能量小，远距离定位时往往淹没在噪声之中难以识别，导致计算误差增大。而信噪比的提高有助于S0模态的识别，减小计算误差，并同时扩大定位范围。最后，理论频散曲线与实际铝板的频散曲线也存在偏差，这在定位时也会同时被引入，因此在定位测试之前如果得到板材的实际频散曲线，将提高本方法的定位精度。

3.2 A0/A0方法定位结果分析

3.2.1 等值线阈值对定位结果的影响

在基于微纳耦合光纤的A0/A0定位方法中,阈值的等值线对A0模态不同频率分量的到达时间判定及最后的定位结果有很大影响。当设定一个较高的阈值时，阈值等值线在某些频率分量上将会缺失，导致其完整性变差，从而引入了误差。通过大量实验发现，为了保证阈值等值线较好的完整性，设定的阈值一般不超过信号最大能量的7%。图10 给出了三种不同阈值下的定位结果，定位的范围为10～80 cm，所有定位中均选择150 kHz和50 kHz的频率分量作为计算频率。

设定一个较高的阈值能够取得较为理想的定位结果，如图10(a)所示，等值线阈值设为5.74%，其最大的定位相对误差也仅有5.33%。当阈值减小后，定位结果也随之变得更差。图10(b)中，等值线阈值降为2.40%，其最大相对误差便达到了9.11%；当设定阈值低于1%后，如图10(c)中阈值设为0.34%，最大相对误差高达38.66%。此外，由图10 中可以得出，阈值等值线对定位范围为10～40 cm的结果影响较小，而对定位范围为40～80 cm的结果影响更大。

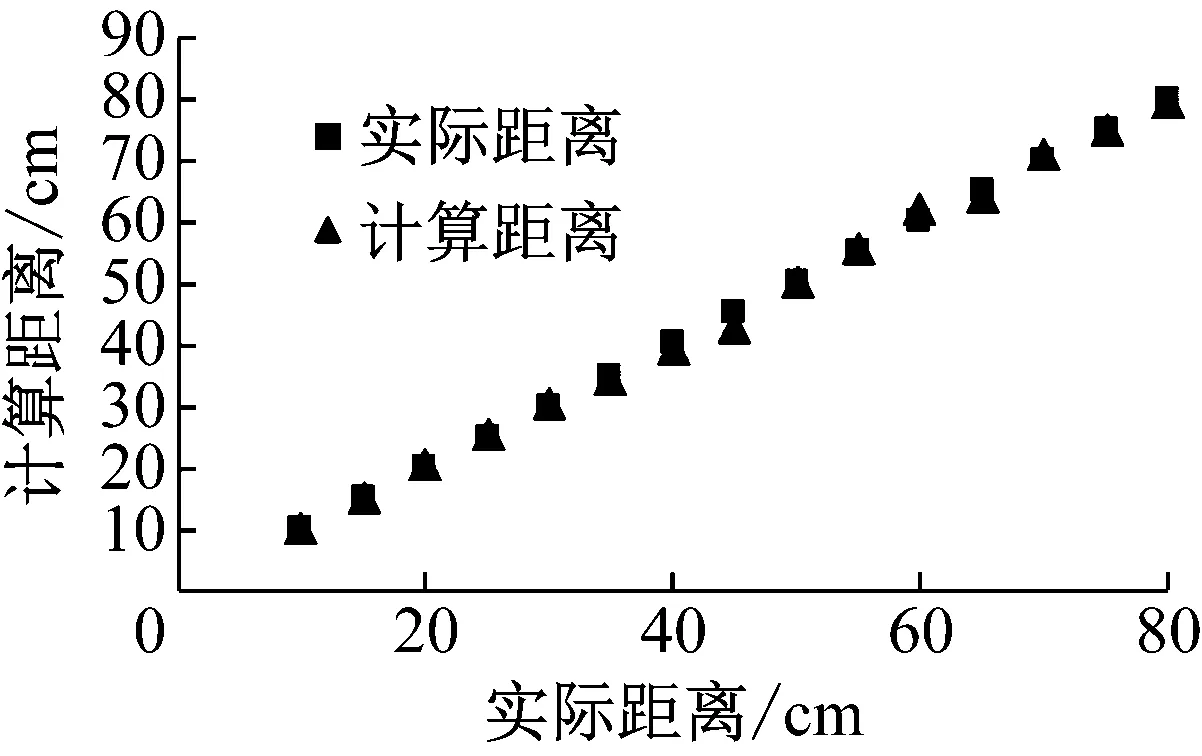
(a) 阈值=5.74%

(b) 阈值=2.40%

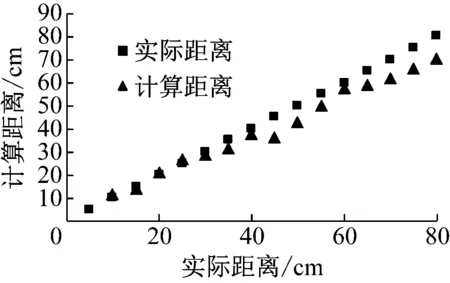
(c) 阈值=0.34%

由图10我们很容易看出设定阈值越小，定位结果的误差就越大。为了便于更好地说明，图11给出了两种不同阈值下的等值线图，其中实线为5.32%的阈值等值线，虚线为0.28%的阈值等值线。从图11中我们可以很清楚地看到0.28%阈值等值线相对于5.32%等值线更为“粗糙”，特别是在200 kHz和40 kHz左右的频率分量到达时间相对于其他分量明显提前，出现这种现象的原因可能是：低阈值等值线导致识别的模态除了A0外还参杂了S0模态及噪声，导致了等值线与A0模态的频散特征不符，影响其到达时间的判定。因此，为了减小这种误判断，设定的等值线阈值不能够太低。

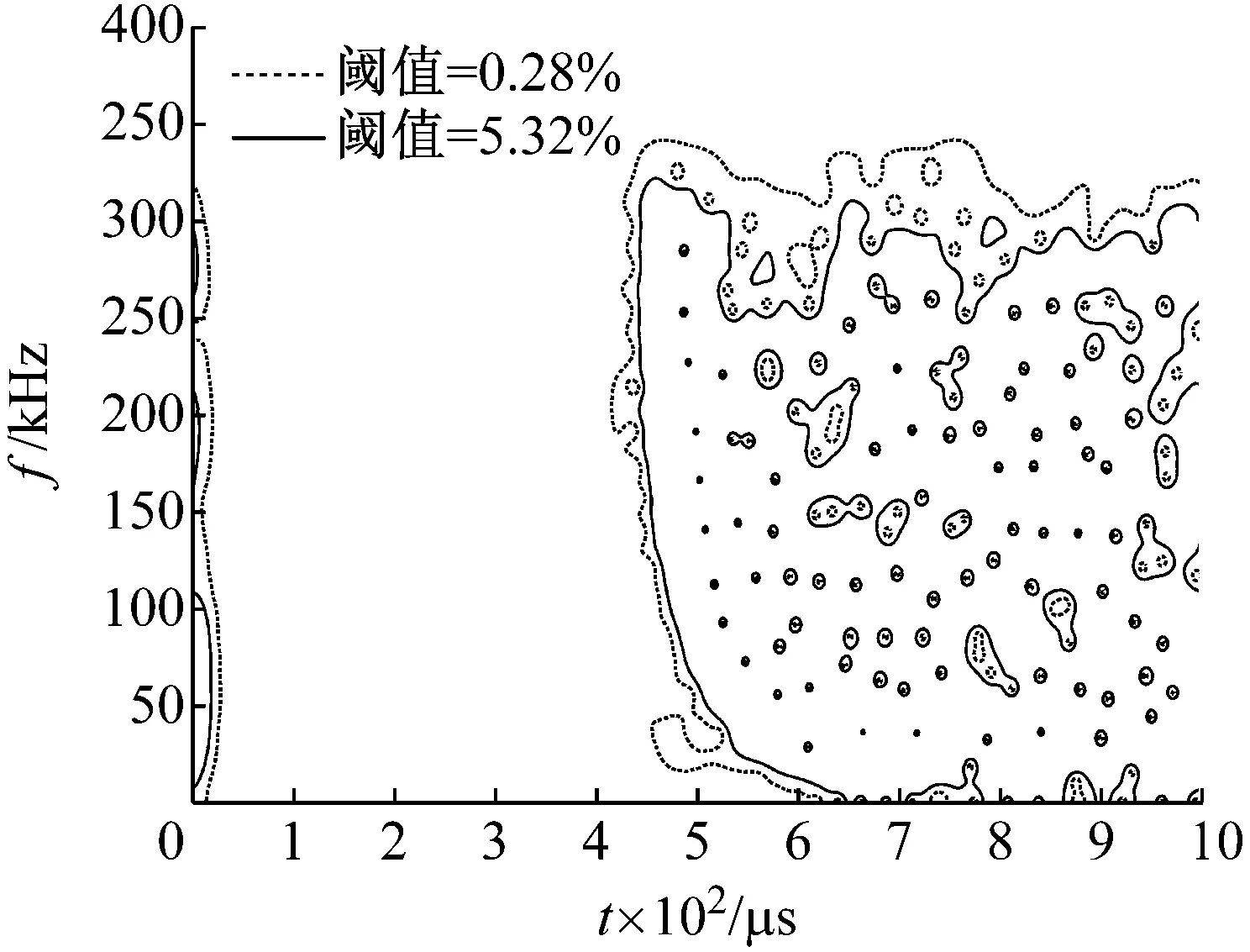
图11 图5(a)中两种不同阈值下的等值线图

综上所述，设定较高的等值线阈值能够减小噪声及S0模态的干扰，从而提高对A0模态各频率分量到达时间的判定精度。然而，等值线阈值也不能设置过高，太高的阈值会使A0模态的完整性变差。因此等值线阈值需要设定在一个合理的范围，对于本文中基于微纳耦合光纤的A0/A0定位方法，合适的等值线阈值设定范围为：信号最大能量的2%～7%。

3.2.2A0/A0定位结果分析

(1) 定位精度及范围

为了探索传感器基于A0模态不同频率分量方法的定位范围，声源由距传感器5 cm开始，每5 cm定位一次，直到铝板的另一端结束。由于受到铝板大小限制，最远定位距离为80 cm。与S0/A0定位方法类似，在定位过程中发现，在10 cm以下时，A0模态频散效应不明显，选取的两个频率分量到达时间有时相同难以区分，从而引入了较大误差。这里定位范围由10 cm开始。不同于S0/A0定位方法，A0/A0定位方法只需要传感器对A0模态具有很好的模态识别能力即可。而微纳耦合光纤对A0模态具有较好的模态识别能力，因此在80 cm处仍能较好地识别A0模态。

表4给出了对应于图5(a)等值线阈值为5.74%下的定位结果，可以看到，基于微纳耦合光纤的A0/A0定位方法取得很好的定位结果。由表可知，其在10～80 cm的定位绝对误差范围为0～2.4 cm，相对误差范围为0～5.3%，表明了该方法具有较高的定位精度。此外，由表4可知定位误差与定位实际距离之间没有明显的关系，仅受到系统误差和随机误差的影响，这表明基于A0模态不同频率分量的定位方法具有较好的均匀性。

表4基于微纳耦合光纤A0/A0定位方法在等值线阈值为5.74%下的定位结果

Tab.4Experimentaldatausingthresholdof5.74%basedonmicro-fibercouplersensorA0/A0locationmethod

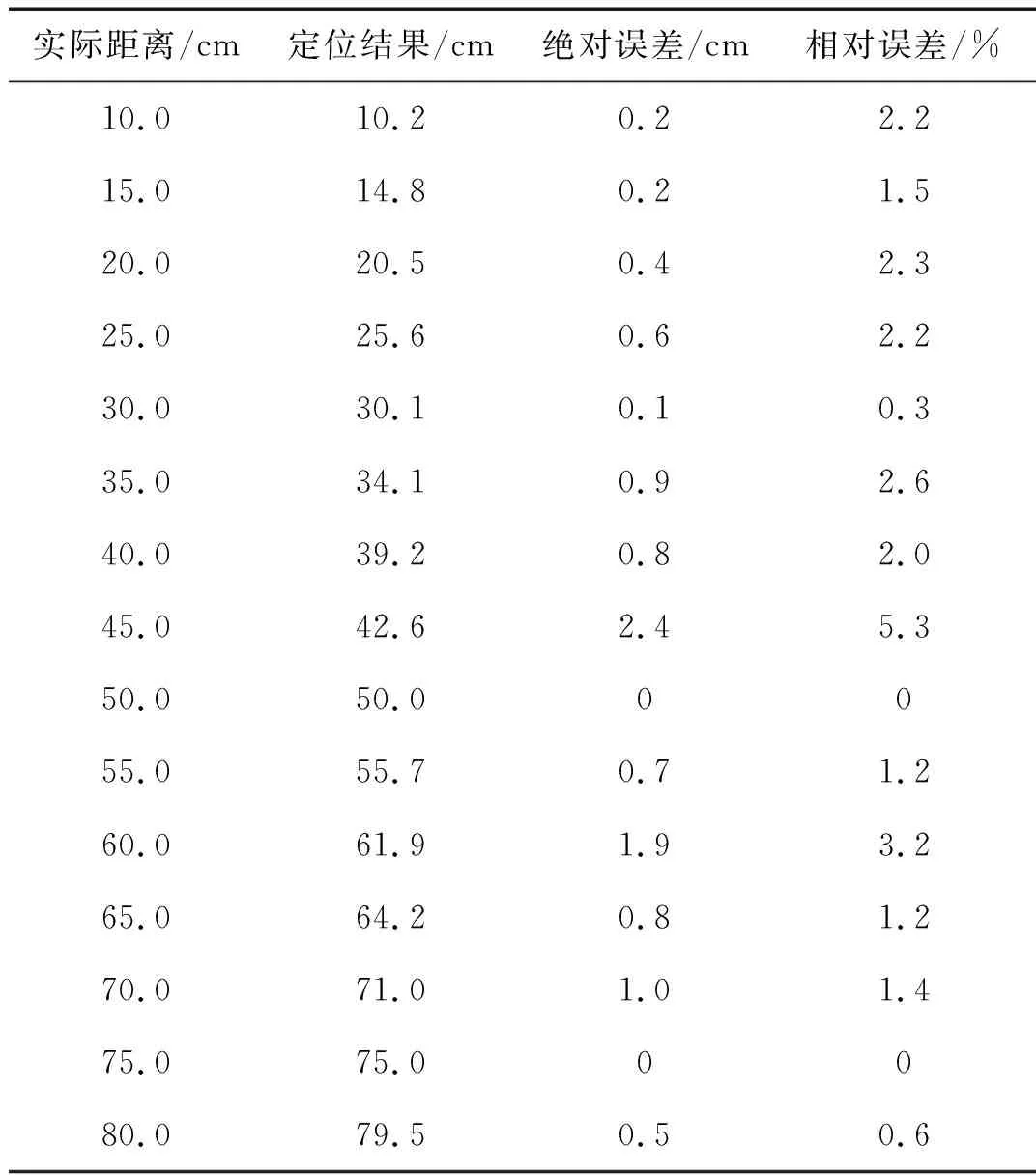
实际距离/cm定位结果/cm绝对误差/cm相对误差/%10.0 10.2 0.2 2.2 15.0 14.8 0.2 1.5 20.0 20.5 0.4 2.3 25.0 25.6 0.6 2.2 30.0 30.1 0.1 0.3 35.0 34.1 0.9 2.6 40.0 39.2 0.8 2.0 45.0 42.6 2.4 5.3 50.0 50.0 0 055.0 55.7 0.7 1.2 60.0 61.9 1.9 3.2 65.0 64.2 0.8 1.2 70.0 71.0 1.0 1.4 75.0 75.0 0 080.0 79.5 0.5 0.6

(2) 定位重复性

为了验证微纳耦合光纤定位的重复性和可靠性，利用铅笔芯断裂法分别在距离传感器d=10 cm、d=45 cm和d=80 cm处重复测试15次，对15次定位结果进行统计。图12给出了三个点重复定位距离的结果分布，其统计数据列于表5。

表5微纳耦合光纤在10cm、45cm和80cm处重复15次定位结果统计

Tab.5Statisticaldataof15timeslocationresultsatd=10cm,d=45cmandd=80cmusingmicro-fibercouplersensor

实际距离/cm平均计算距/cm绝对偏差/cm绝对标准差/cm10.009.980.020.3545.0044.780.220.7980.0079.640.361.63

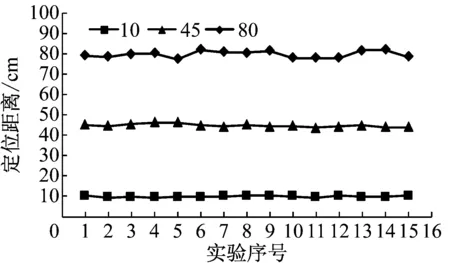
图12 微纳耦合光纤在10 cm、45 cm和80 cm处重复15 次定位结果分布

由图12可看出，无论是近距离10 cm的定位结果，还是远距离80 cm的定位结果，均表明了微纳耦合光纤的重复性定位具有很好的效果。其中，10 cm的定位结果最为准确，波动性最小，45 cm的定位结果出现波动，而80 cm的定位结果波动范围相对较大，这可能是由于系统误差和随机误差随着定位距离的增大而增大所导致。

表5列出了三个位置15次重复定位的绝对偏差、平均计算距离及其绝对标准差，平均计算距离及其绝对偏差为15次计算结果的平均值及其与实际结果的绝对差值，表征了15次重复定位实验的正确度。由表5可知，10 cm处的平均定位结果为9.98 cm，其绝对误差仅为0.02 cm，45 cm和80 cm处的平均定位结果分别为44.78 cm和79.64 cm，其绝对偏差值为0.22 cm和0.36 cm。总的来看，三个点重复定位的绝对偏差不超过0.4 cm，表明基于A0模态不同频率分量的定位方法具有较高的定位精度。绝对标准差能够反映出数据的离散程度，由表5 可知，10 cm处定位的结果重复性最高，其绝对标准差为0.35 cm，45 cm处定位的结果重复性次之，绝对标准差为0.79 cm，80 cm处定位的结果重复性有所下降，绝对标准差为1.63 cm。这主要是由于信号随着传播距离的增加而有所衰减，同时也可能伴随着波模态的反射叠加、模态转换等情况。综上所述，三个点的绝对标准差不超过2 cm，表明基于A0模态不同频率分量的定位方法具有较好的重复性。

(3) 误差分析

基于微纳耦合光纤的A0/A0方法定位误差主要来自三个方面：① 信号A0模态完整性；② 等值线阈值的选取； ③ 两个计算频率分量的选取。

信号A0模态完整性指的是在信号的Gabor分布图中，A0模态高频分量到达时间快，低频分量到达时间慢，且分布连续符合图 1的频散曲线。A0模态不完整的信号某些频率分量微弱甚至没有，导致该频率被选为计算频率时会导致到达时间误判断，这样从而导致定位结果的偏差。因此，本方法更适用于A0模态完整性高的信号。等值线阈值的设定也会影响信号频率分量的到达时间，设定阈值不同，计算频率分量的到达时间不同，两个频率分量到达时间差也会不同，从而引入计算误差；这样，A0模态两个不同频率分量的选取也影响计算结果，这实际上还是由于理论频散曲线和实际板材的频散曲线不相同所导致，因此，在应用本方法进行定位之前需要获取板材的实际频散曲线，以提高定位精度。

3.3 两种定位方法的对比和评估

由于S0/A0定位方法和A0/A0定位方法定位范围不同，且重复定位位置也不同，为了便于两者的比较，需要将其计算结果的绝对值转换为相对值。为了比较两者的定位精度，分别计算了两者的定位相对误差，即定位相对误差=(定位绝对误差/实际距离)×100%；而为了比较两种方法定位的重复性，引入相对标准差，即相对标准差=(绝对标准差/平均值)×100%。相对标准差既能够表征重复定位实验的精密度，同时也能克服平均值的影响，能够用于不同平均值下精密度的横向比较。这样，得到了基于微纳耦合光纤S0/A0定位方法和S0/A0定位方法各项指标，列于表6中。

首先，从自动化程度来看，S0/A0定位方法要优于A0/A0定位方法。S0/A0定位方法能够根据所测信号的Gabor变换自动选取S0模态能量峰值对应的频率作为计算频率，不需人工选取，且在该计算频率下两个模态的到达时间可通过峰值法直接确定，能够实现定位算法的程序化，因此该方法能够实现声发射源的自动定位；而A0/A0定位方法的计算频率选择较为灵活，对于不同的频率选择组合得到的定位结果也不同，目前还尚未形成统一的频率选择策略，实现定位算法的程序化及声发射源的自动定位还有待研究。

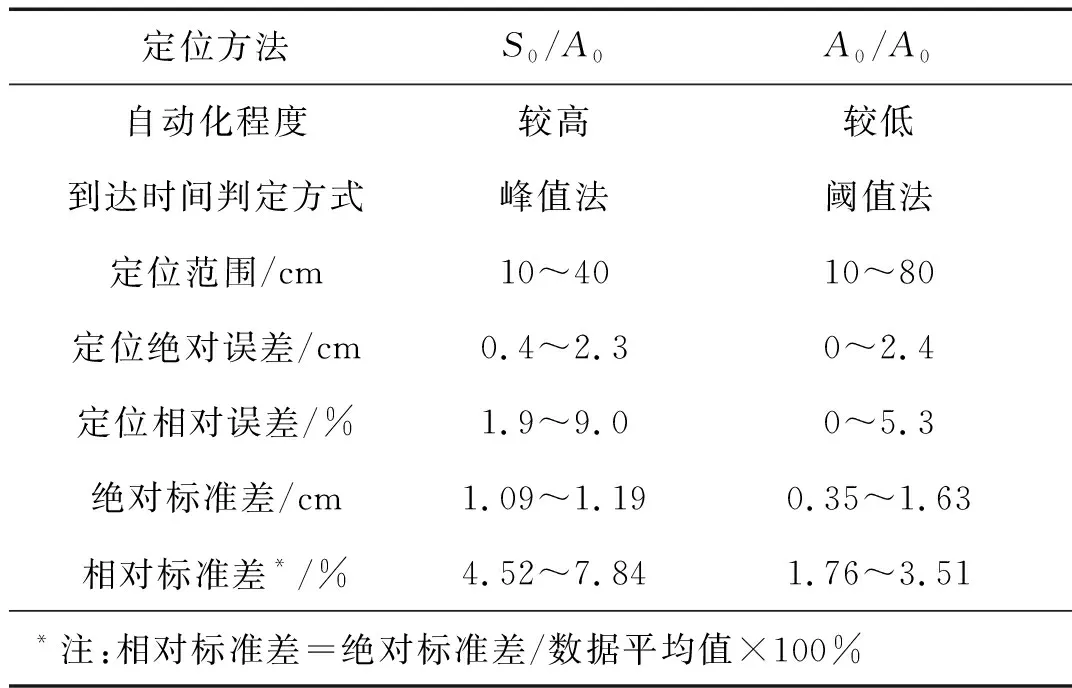
表6 基于微纳耦合光纤两种定位方法的比较

其次，到达时间判定方式来看，A0/A0定位方法要优于S0/A0定位方法。S0/A0定位方法是采用峰值法判定两种模态的到达时间，这是由于S0模态相对于A0模态能量很小，仅仅略高于噪声能量，因此需要设定两种不同的阈值分别判定S0模态和A0模态的到达时间，这两种阈值的选择同样比较灵活，若以阈值法判定会带来较大的误差，因此在S0/A0定位方法中采用峰值法，但这也受到了模态反射叠加对到达时间判定的影响，从而影响了定位精度。而在A0/A0定位方法中，采用的是同一模态(A0)下不同频率分量计算，两个频率分量的到达时间可通过同一个阈值判定，且最终计算时是根据两个频率分量达到时间差进行的，因此该方法采用阈值法更为合适。

从定位范围来看，A0/A0定位方法要优于S0/A0定位方法。这主要是由于S0模态能量本身较小，且本文中的微纳耦合光纤对S0的模态识别能力不够。

从定位精度来看，A0/A0定位方法要优于S0/A0定位方法。尽管从定位绝对误差来看，两者最大定位绝对误差均不超过2.5 cm，但从定位相对误差来看，S0/A0定位方法在10～40 cm范围内定位相对误差为1.9%～9.0%，A0/A0定位方法在10～80 cm的定位相对误差为0～5.3%，几乎为S0/A0定位方法的一半。对比表1和表3更能清楚的得出此结论。

从定位重复性来看，A0/A0定位方法要优于S0/A0定位方法。从绝对标准差来看，S0/A0定位方法重复定位25 cm的绝对标准差为1.19 cm，而A0/A0定位方法重复定位45 cm的绝对标准差仅为0.79 cm；从相对标准差来看，S0/A0定位方法在10～40 cm范围内定位相对标准差为4.52%～7.84%，而A0/A0定位方法在10～80 cm的定位相对标准差仅为1.76%～3.51%，表明了A0/A0定位方法的重复性要明显高于S0/A0定位方法。

综上所述，基于微纳耦合光纤的S0/A0定位方法自动化程度高，适用于10～40 cm范围的声发射源定位；A0/A0定位方法的定位精度和定位重复性优于S0/A0定位方法，且定位范围可达10～80 cm，但计算频率选择为人工选取，自动化程度有待进一步提高。

4 结 论

本文搭建了基于微纳耦合光纤传感器的定位实验平台，分别利用S0/A0定位方法和A0/A0定位方法对模拟声发射源进行了线性定位。首先，利用S0/A0定位方法对5～40 cm模拟声发射源进行了线性定位，分析了Gabor变换时间分辨率对模态识别准确度的影响，并对定位结果进行了详细分析；利用A0/A0定位方法对10～80 cm模拟声发射源进行了线性定位，分析了等值线阈值对定位结果的影响，并对定位结果进行了详细分析；最后，分别从自动化程度、定位精度、定位范围、定位重复性等方面对两种方法进行了对比。得到主要结论如下：

(1) 利用S0/A0定位方法进行定位时，Gabor变换时间分辨率不能太低，否则会导致S0模态识别的误判断，增大定位误差；在定位过程中，声源距离太近会因为S0、A0模态混合难以区分而增大定位误差，声源距离太远会由于传感器对S0模态识别能力减弱而难以捕捉；该方法在10～40 cm范围内取得了较好的定位结果，绝对定位误差不超过2.3 cm，相对定位误差不超过9%，考虑到传感器本身长4.4 cm，因此可认为定位精度是可接受的；此外，分别在15 cm处和25 cm处进行了13次的重复定位实验，重复定位的绝对标准差不超过1.19 cm，相对标准差不超过7.84%，因此可认为该定位方法有较好的重复性。

(2) 利用A0/A0定位方法进行定位时，等值线阈值对定位结果影响较大，在满足A0模态完整性的前提下，应尽量增大阈值，减小S0模态及噪声信号对A0等值线的干扰，从而提高定位精度；在定位过程中，声源太近同样会导致模态不同分量几乎同时到达难以区分，增大了定位误差，而微纳耦合光纤的A0模态识别能力较好；因此，该方法能在10～80 cm范围均取得了较好的定位结果，定位的绝对误差不超过2.4 cm，相对误差不超过5.3%，可以认为该方法是准确有效的；此外，分别在10 cm、45 cm和80 cm处进行了15次的重复定位实验，重复定位的绝对标准差不超过1.63 cm，相对标准差不超过3.51%，表明了该方法具有较高的重复性。

(3) 对比分析了基于微纳耦合光纤的S0/A0定位方法和A0/A0定位方法的优缺点，由于微纳耦合光纤的A0模态识别能力更强，因此在定位精度、定位范围、及定位重复性等方面A0/A0定位方法要优于S0/A0定位方法；然而，S0/A0定位方法计算频率选择、模态到达时间均可自动实现，相比于需要人工选择计算频率的A0/A0定位方法其自动化程度更高，在实际应用中更具有优势。