压缩波束形成声源识别的改进研究
2019-01-23张晋源褚志刚
张晋源, 杨 洋, 褚志刚
(1.重庆工业职业技术学院 车辆工程学院,重庆 401120;2.重庆大学 汽车工程学院,重庆 400030)
波束形成是实现声源识别的有效技术,凭借测量速度快、适宜中长距离测量、易于布置等优势,已广泛应用于航空航天、高速列车、汽车等领域[1-2]。该技术利用传声器阵列测量声压信号,基于特定算法后处理这些信号,使真实声源所在位置的输出量被加强而其它位置的输出量被衰减,从而识别声源。延迟求和(Delay And Sum, DAS)是常用算法,其对各传声器测量的声压信号进行“相位对齐”和“求和运算”,简单易实现,计算效率高,但低频空间分辨率差且高频旁瓣污染严重,这些缺陷使声源识别结果承受高不确定性。为克服DAS的缺陷,一些学者提出了反卷积算法,典型代表有反卷积声源成像(Deconvolution Approach for the Mapping of Acoustic Sources, DAMAS)、非负最小二乘(Non-Negative Least Squares, NNLS)、Richardson-Lucy (RL)等。这些算法将DAS的输出看作声源分布与点传播函数的卷积,通过反卷积移除点传播函数来重构声源分布,能显著提高空间分辨率并衰减旁瓣,但因涉及大维数矩阵运算和多次迭代而存在耗时严重的缺陷[3-5]。近年来,基于压缩感知框架的压缩波束形成[6-9]脱颖而出,其不仅能提供高分辨率低污染声源成像,而且享有高效率,已备受关注。
压缩波束形成在阵列传声器测量声压信号、感知矩阵、声源分布及噪声干扰间建立线性欠定方程组,通过施加稀疏约束来定解该方程组,从而重构声源分布。传统求解方法中,施加稀疏约束体现为直接最小化声源分布向量的l1范数,存在噪声干扰时,其重构结果与真实结果间存在一定偏差,该偏差使声源无法被直接准确量化。本文致力于改善该问题、提高压缩波束形成的性能,给出的求解方法称为迭代重加权l1范数最小化,即通过迭代方式求解声源分布,且每次迭代中最小化引入的加权矩阵与声源分布向量的乘积的l1范数。
本文首先在阐明传统压缩波束形成基本理论的基础上给出迭代重加权l1范数最小化方法,然后基于仿真模拟的声源识别结果验证所给方法的优势,最后基于扬声器声源识别试验验证仿真结论的正确性及所给方法在实际应用中的有效性。
1 基本理论
1.1 传声器阵列测量
图1为传声器阵列测量示意图,符号“●”表示传声器,rm(m=1,2,…,M)为m号传声器的坐标向量,M为传声器总数,r0i为i号声源的坐标向量,si为i号声源的强度。假设声源辐射球面声波,则声源在m号传声器处产生的声压可表示为
(1)
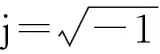
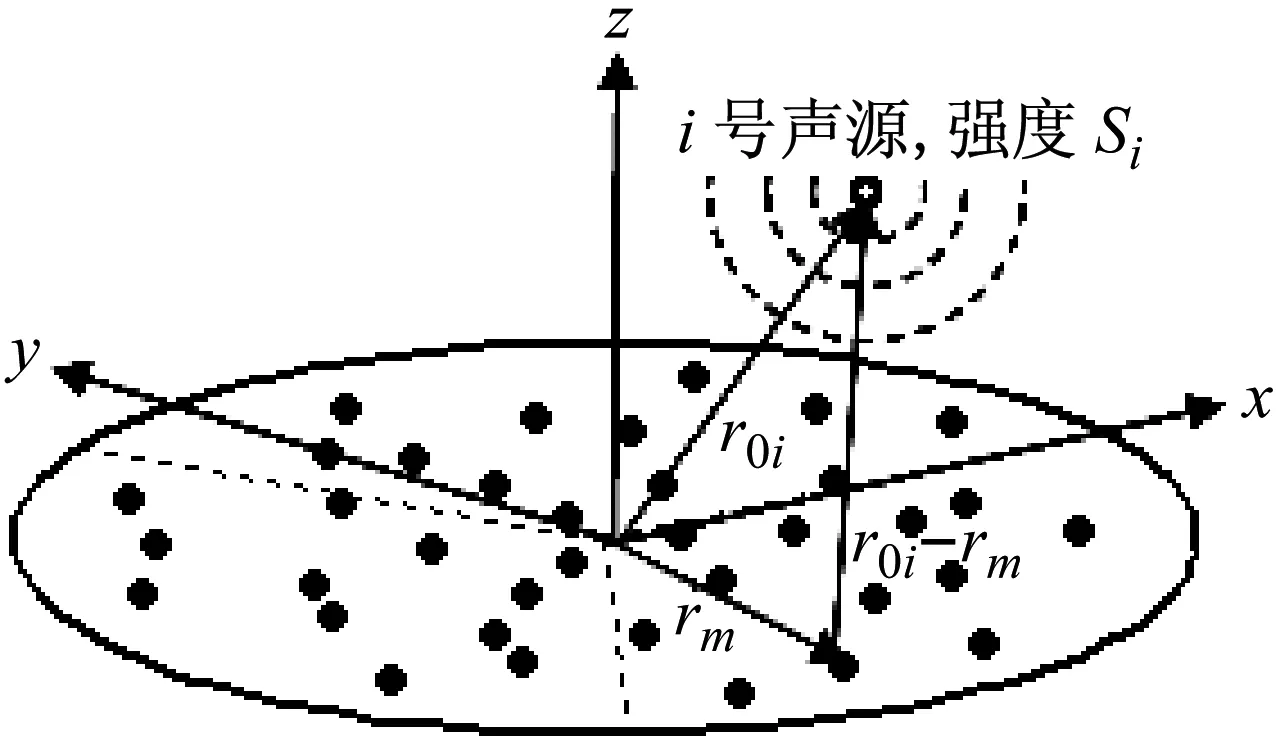
图1 传声器阵列测量示意图
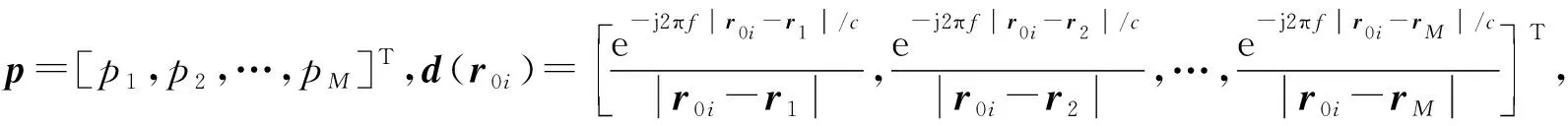
(2)
存在噪声干扰n时,测量声压p★可表示为
p★=p+n
(3)
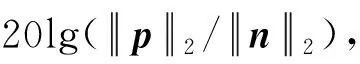
1.2 传统压缩波束形成
设定声源面并离散为一组网格点,记rg(g=1,2,…,G)为g号网格点的坐标向量,G为网格点总数。假设声源落在这些网格点上,则阵列传声器测量的声压信号可表示为
p★=Fs+n
(4)
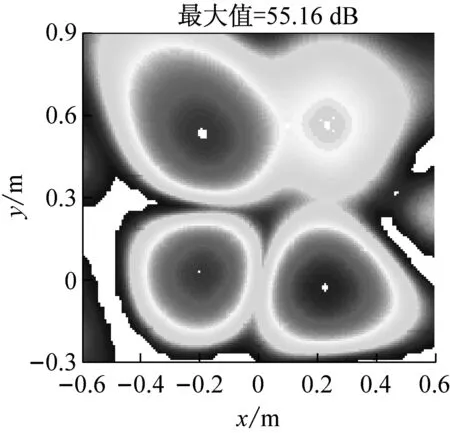
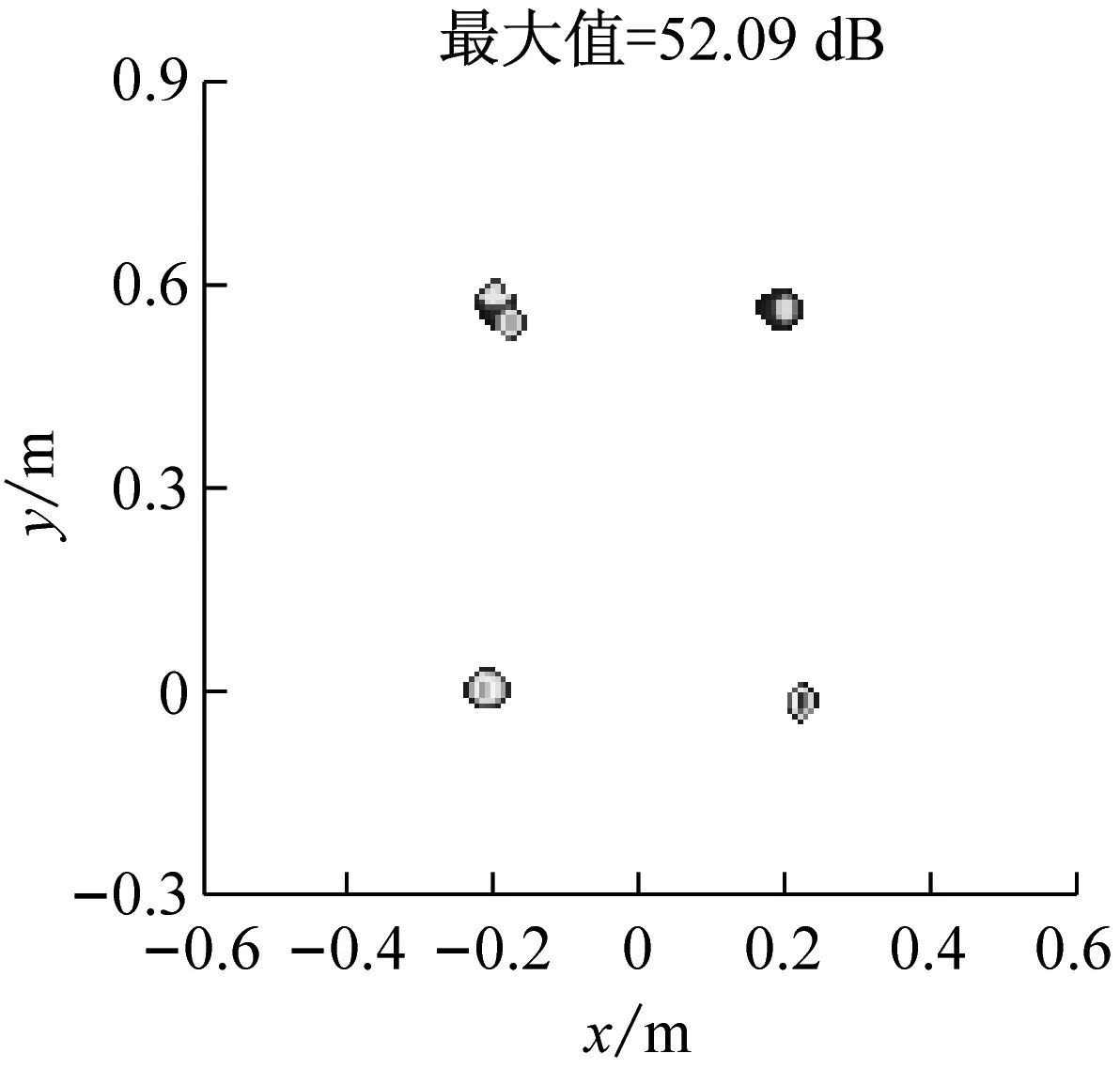
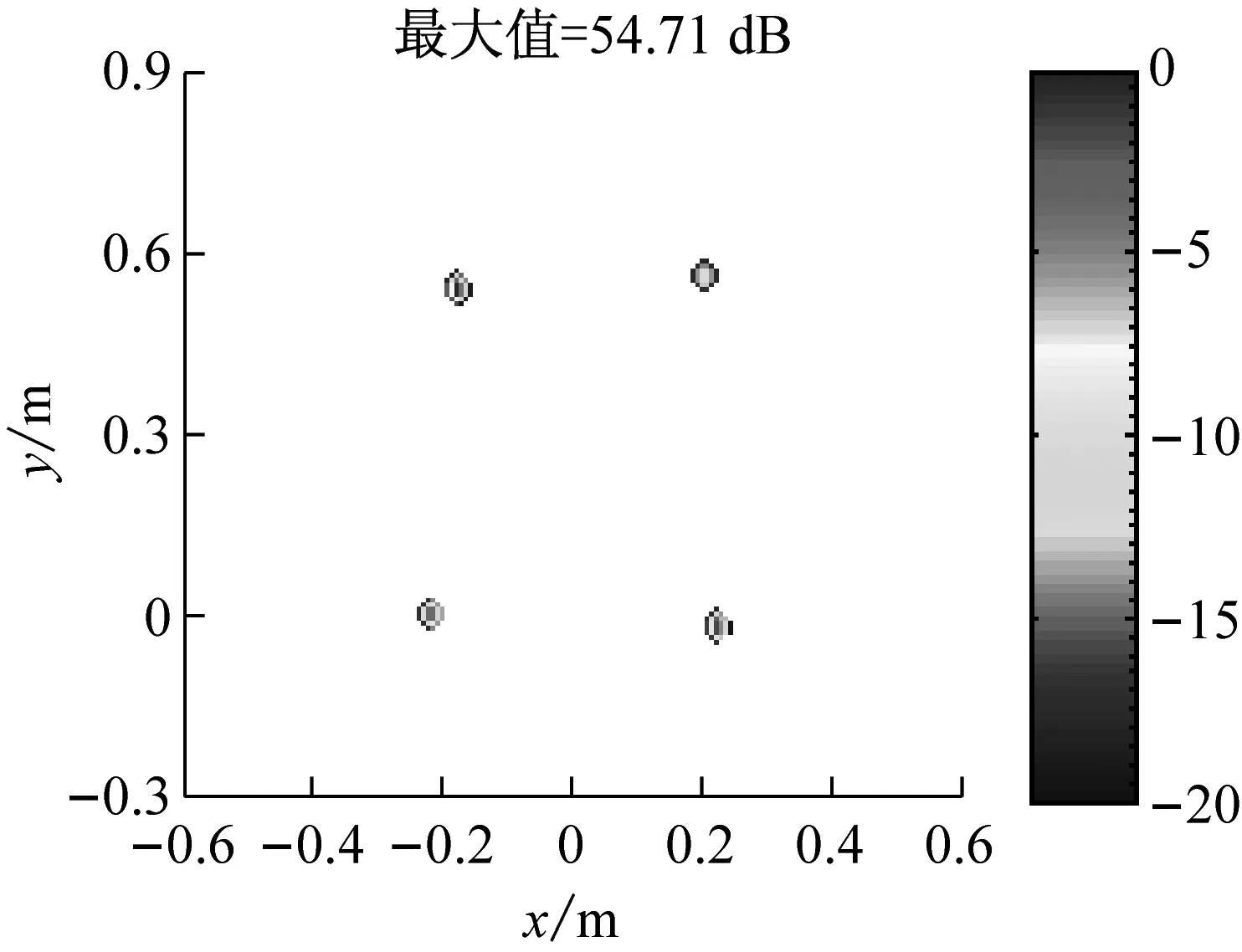
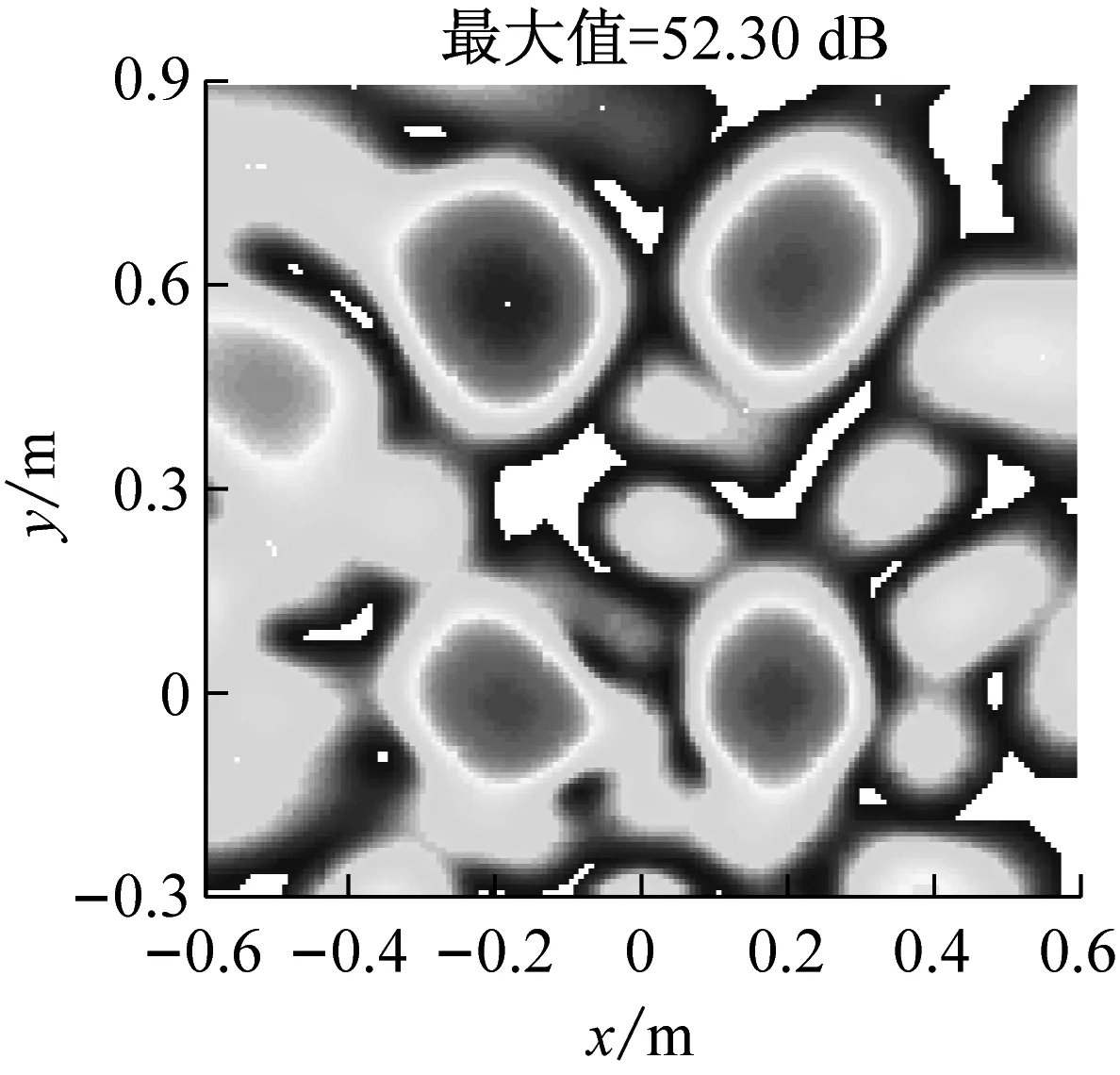
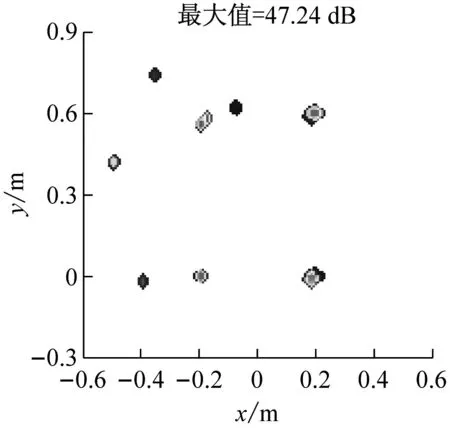
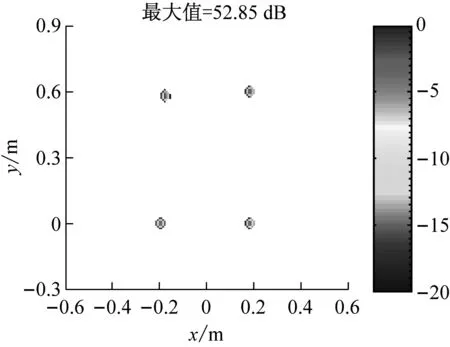
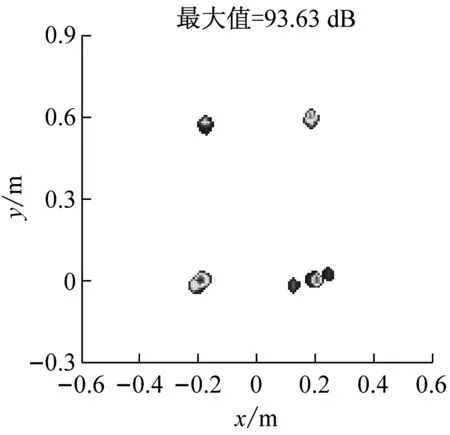
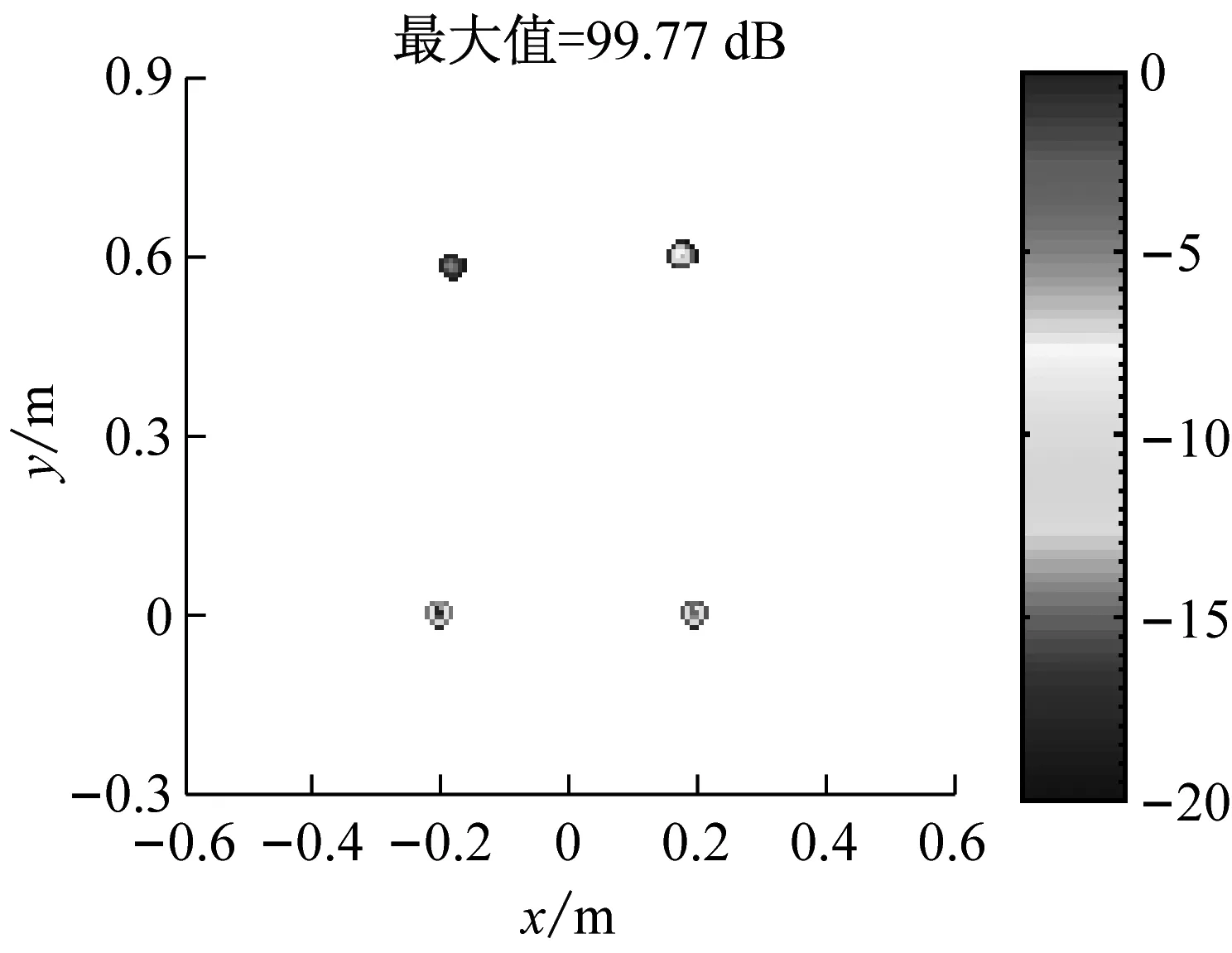
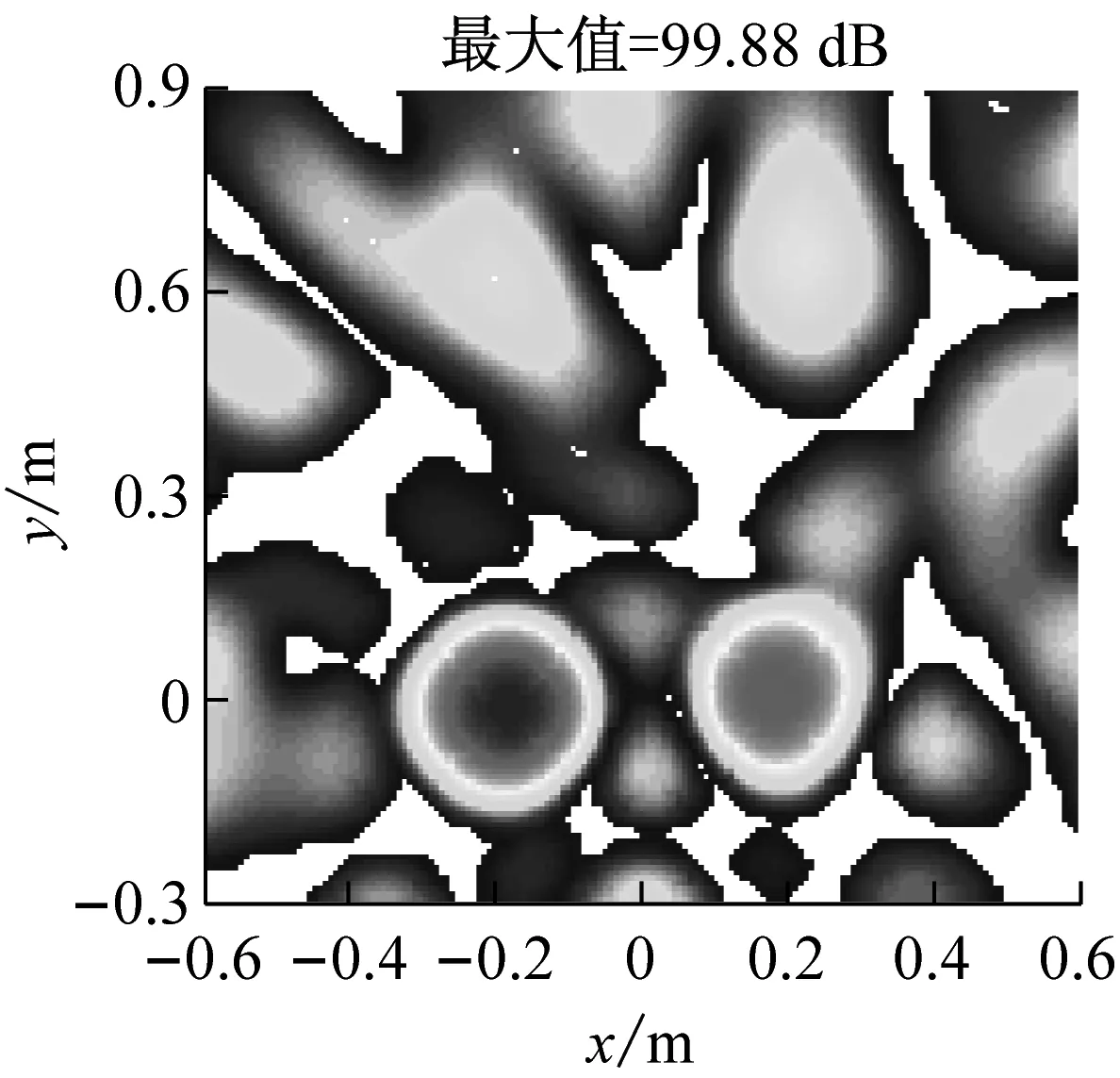
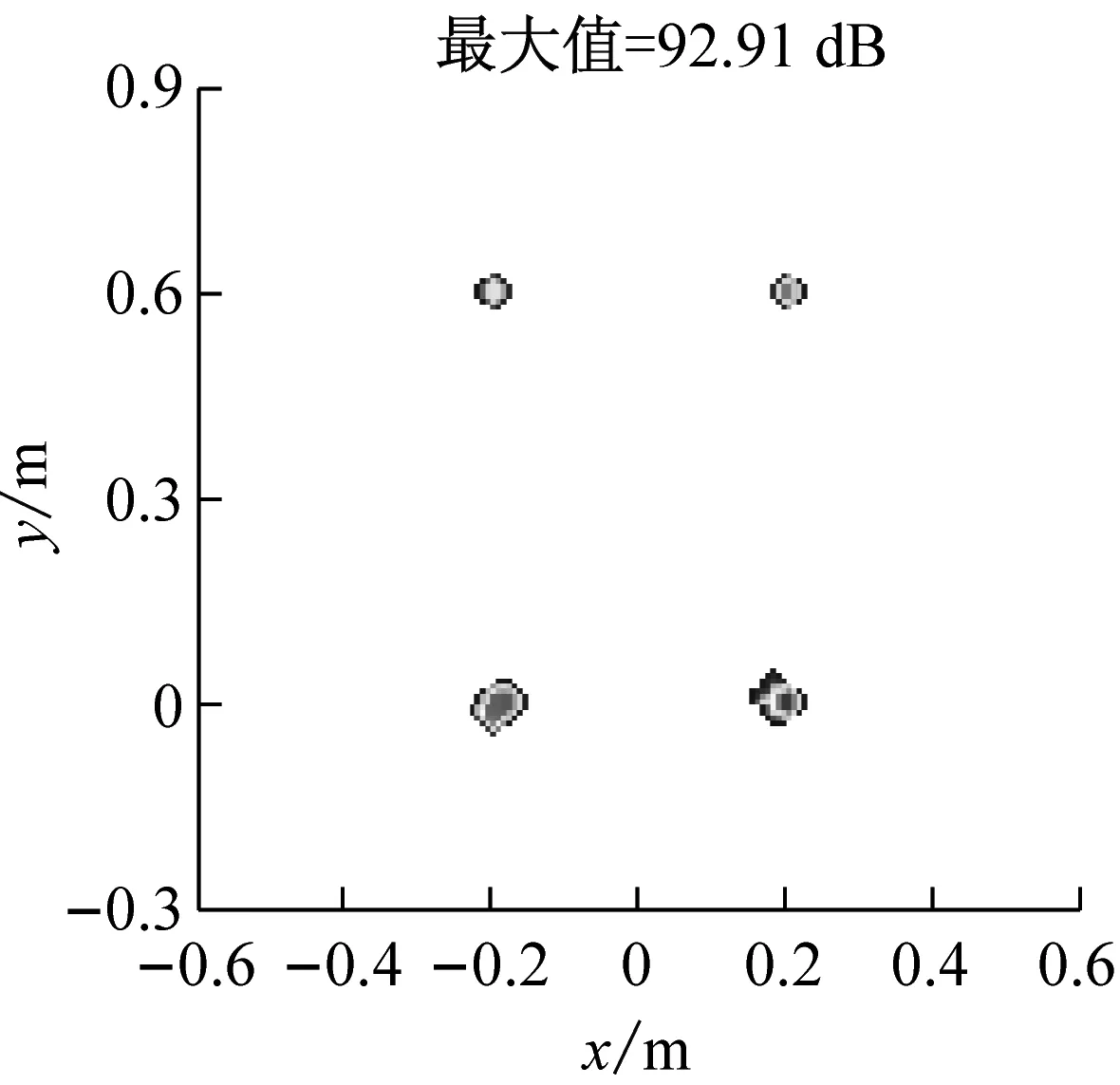
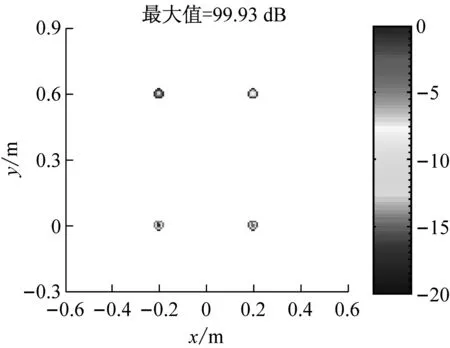
式中:F=[d(r1),d(r2),…,d(rG)]为M×G维感知矩阵,每一列为位于一个网格点上的单位强度点声源在各传声器处产生的声压,s=[s1,s2,…,sG]T为未知的声源分布向量。通常,M (5) (6) (7) (8) 那么,式(7)可写为 (9) 为验证所给迭代重加权l1范数最小化方法的优势,以图1所示传声器阵列为例进行仿真模拟,具体流程为:首先,假设声源分布(声源位置、声源强度及声波频率)和噪声干扰,根据式(1)~(3)计算各传声器测量的声压信号;然后,设定声源面并离散为一组网格点,构建感知矩阵;最后,分别基于DAS(输出量为FHp★/M,上标“H”表示转置共轭)、式(5)所示的传统压缩波束形成及式(8)和(9)所示的迭代重加权l1范数最小化压缩波束形成重构声源分布并成像。迭代重加权l1范数最小化中,迭代次数设为3。 (a) DAS (b) 传统压缩波束形成 (c) 迭代重加权l1范数最小化压缩波束形成 (a) DAS (b) 传统压缩波束形成 (c) 迭代重加权l1范数最小化压缩波束形成 为验证仿真结论的正确性及所给方法在实际应用中的有效性,在半消声室内进行试验。图4为试验布局示意图,将稳态白噪声信号激励的分别位于(-0.2,0,1) m、(0.2,0,1) m、(-0.2,0.6,1) m、(0.2,0.6,1) m的四个扬声器作为声源,采用Brüel & Kjr公司、直径0.65 m、集成4958型传声器的36通道扇形轮阵列测量声压信号。20~20 000 Hz频段内,该半消声室的本底噪声约16 dB,扬声器声源在阵列传声器处产生的声压约90 dB。各传声器测量的声压信号经PULSE 3560D型数据采集系统同时采集并传输到PULSE LABSHOP中进行快速傅里叶变换,得声压频谱。然后,设定声源面并离散为一组网格点,构建感知矩阵,分别基于DAS、传统压缩波束形成及迭代重加权l1范数最小化压缩波束形成重构声源分布并成像。与仿真模拟中一致,这里,迭代次数也设为3。 图4 试验布局示意图 图5和图6分别给出了2 000 Hz和4 000 Hz时的成像图,显见,DAS承受差的空间分辨率和高的旁瓣污染,传统压缩波束形成和迭代重加权l1范数最小化压缩波束形成均有效克服了该缺陷,且后者效果更佳。图5(a)中,DAS输出的四个主瓣峰值依次为54.09 dB、55.16 dB、54.24 dB、48.32 dB,基于“声源可分辨时,DAS输出的主瓣峰值约等于真实声源强度”的事实,将这些主瓣峰值看作真实声源强度来量化传统压缩波束形成和迭代重加权l1范数最小化压缩波束形成的重构准确度。图5(b)中,传统压缩波束形成输出的四个主瓣峰值依次为46.45 dB、52.09 dB、47.45 dB、43.75 dB,与真实声源强度的偏差最多达约8 dB,最少也有约3 dB,图5(c)中,迭代重加权l1范数最小化压缩波束形成输出的四个主瓣峰值依次为53.51 dB、54.71 dB、53.71 dB、48.20 dB,与真实声源强度的偏差不超过0.6 dB,表明相比于传统压缩波束形成,迭代重加权l1范数最小化压缩波束形成重构的声源分布更接近真实声源分布。图6亦符合该规律,不重复说明。这些试验结论与仿真结论一致,验证了仿真结论的正确性,同时表明所给方法对实际声源有效。 为改进传统压缩波束形成的声源识别性能,本文给出迭代重加权l1范数最小化方法,并基于仿真模拟和验证试验检验其优势,所得结论如下: (1) 相比于传统压缩波束形成,迭代重加权l1范数最小化压缩波束形成能进一步提高空间分辨率、衰减旁瓣污染,获得更清晰明确的声源成像图。 (2) 迭代重加权l1范数最小化压缩波束形成能有效降低传统压缩波束形成对声源分布的重构偏差。 (3) 迭代重加权l1范数最小化压缩波束形成对实际声源有效。 (a) DAS (b) 传统压缩波束形成 (c) 迭代重加权l1范数最小化压缩波束形成 (a) DAS (b) 传统压缩波束形成 (c) 迭代重加权l1范数最小化压缩波束形成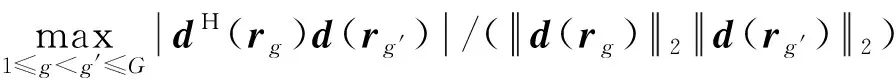
1.3 迭代重加权l1范数最小化
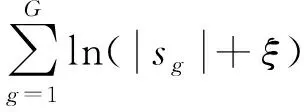
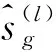
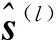
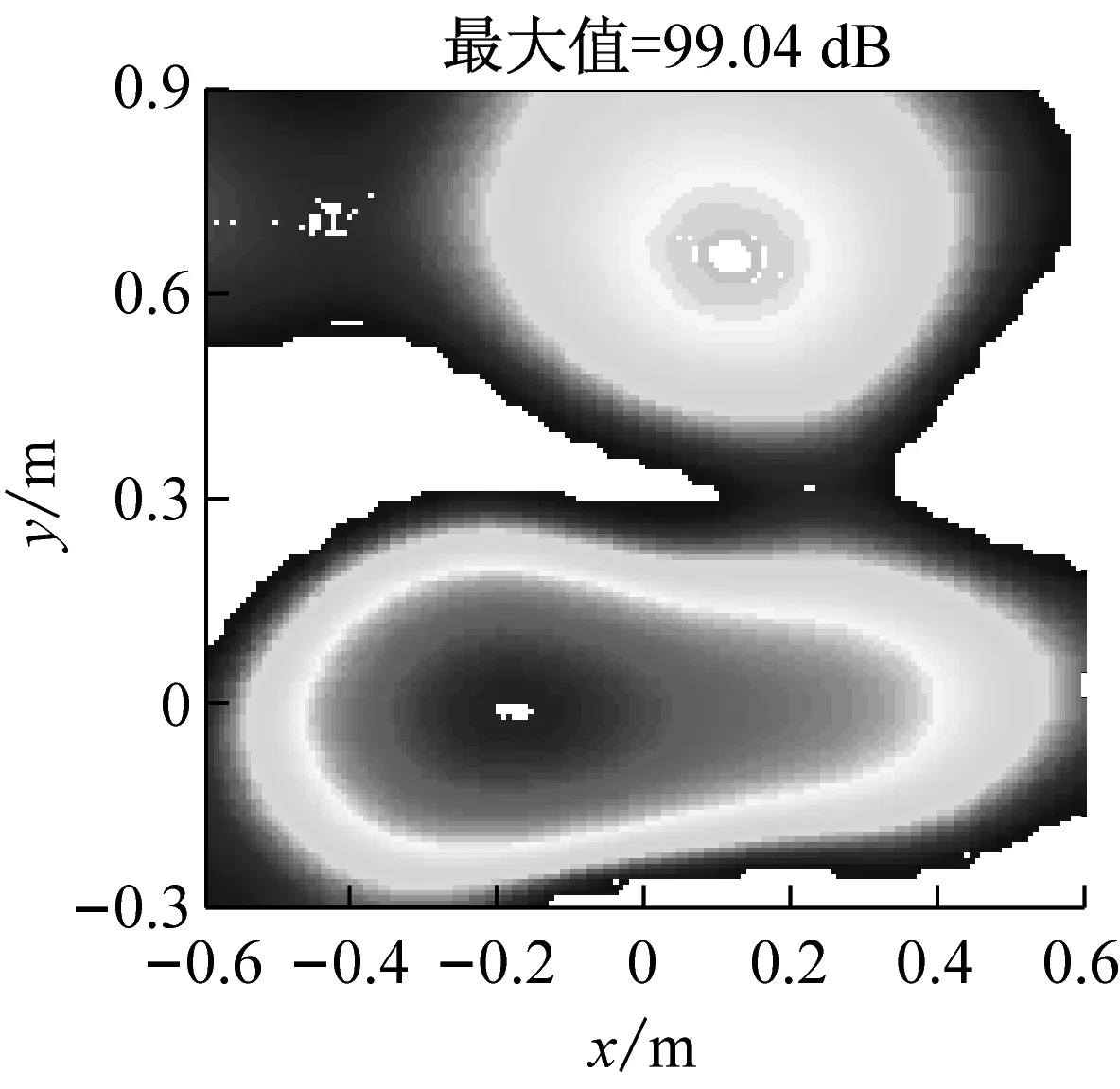
2 仿真模拟
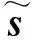
3 验证试验

4 结 论