基于振动模态分析的轴承缺陷自动监测系统研究*
2019-01-23兰叶深毛建辉徐建亮周燕飞
兰叶深,毛建辉,徐建亮,周燕飞
(1.衢州职业技术学院 机电工程学院,浙江 衢州 324000;2.浙江大学 机械工程学院,杭州 310027)
0 引言
近年来轴承的缺陷诊断[1-3]逐渐受到重视,而旋转机器所产生的大部份问题是由轴承损坏引起的,早期在监测轴承损坏的过程中,以高频解调分析法[4-5]来观察高频的振动特性,再经由轴承的解调频谱上的频率特性,来判断轴承是否损坏。国内外学者[6-10]做了大量的研究,虽然这些方法皆能有效的分析轴承组件的缺陷,其中,时域分析方法与统计方法仍受轴承转速、损坏形式以及负载情况的影响,当转速增加或负载减少时,会使得机率峰度变小,因此较难以机率峰度清晰辨别机械轴承缺陷;且Heng等[11]指出当轴承转速高于1500rpm时,机率峰度分析法与峰值因数则会逐渐难以正确判断轴承损坏,对于外环损坏的情况更是完全无法判断。因此,本文将采用Filter法进行设计类比解调电路,并以计算包络信号间的相关系数,建立轴承相关系数诊断指标,通过对Filter法与FFT法的分析结果进行比较,实验数据显示,Filter法完全满足轴承缺陷的实时分析诊断,且在轴承转速达到2400rpm时,也能够在最短时间内判断轴承是否存在缺陷。
1 理论分析
希尔伯特转换(Hilbert transform)[12]常应用在振动信号的解调分析上,其中Filter-based Hilbert transform(基于类比解调电路)适用于硬件上,而在FFT-based Hilbert transform(基于高频解调分析)适用于软件上;前者在应用上滤波特性受其截止频率的衰减斜率影响,一般而言易产生较大的信号扭曲;而后者滤波特性则具有完美的截止频率特性,然而FFT却需大量数据进行批次运算,因此无法达到实时运算,并且随着率波频率增高,而需更高阶的微处理器进行运算。相较于前述FFT-based Hilbert transform的限制,Filter-based Hilbert transform则无此缺失,因此着眼于能达到实时振动信号分析,本文将采用Filter-based Hilbert transform进行系统设计,并采用较高阶的滤波方法以降低信号扭曲。
1.1 FFT-based Hilbert transform解调振动信号原理
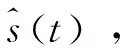

(1)
式(1)经傅里叶变换,可得:
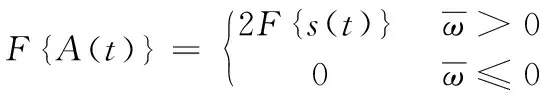
(2)
式(2)经逆傅里叶变换,可得:
A(t)=F-1{2F{s(t)}}
(3)
最后可得,单一模态轴承振动信号s(t)的包络信号为:
e(t)=|A(t)|=|F-1{2F{s(t)}}|
(4)
1.2 Filter-based Hilbert transform解调振动信号原理
本文中,将以Filter-based Hilbert transform(以下简称Filter法)应用在硬件上,利用加速规的电路放大器来获取原始振动信号如图1所示,接着应用高频解调分析技术,设计类比解调电路分析诊断轴承缺陷振动信号,设定带通滤波器所要的带宽,由带通滤波器获取振动信号的单一振动模态的振动信号,再将带通滤波后的信号由精密全波整流器,并经过低通滤波器,以获得此单一模态的包络信号如图2所示。
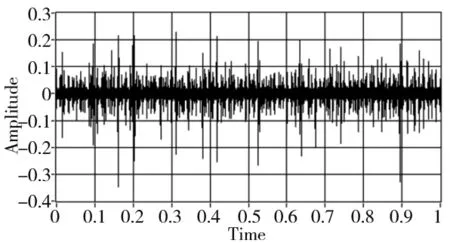
图1 原始振动信号
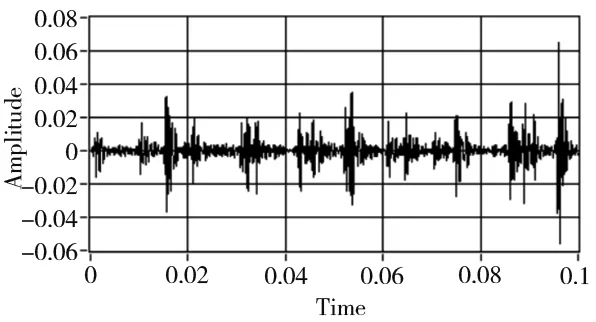
图2 包络信号的时域特性
1.3 相关系数分析法
利用类比解调电路所求得的包络信号,计算出共振模态间的相关系数(Correlation coefficient)[13],可以选取两个共振模态的包络信号求出此组共振模态的相关系数,如下式:
(5)
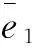
2 系统设计
经由前述分析,进一步设计以硬件电路来实现信号处理的整个过程,以ARM Cortex-M3芯片为核心进行轴承缺陷诊断系统硬件架构设计,轴承缺陷振动信号处理流程及系统架构如图3所示。首先由加速规测量振动信息后,经由所设计的高频解调分析电路,获得两组包络信息,接着以Cortex-M3芯片进行轴承缺陷诊断指标的分析计算,通过LCM显示数值信息,再依实验分析结果,设定轴承正常运作的临界阀值,以监测轴承的缺陷与送出警示信号,完成轴承缺陷警示系统设计,应用于轴承缺陷的自动监测与报警。
将获取的振动信号经由两组MAX274带通滤波芯片进行带通滤波,以获取两组不同机械振动模态。其中,MAX274带通滤波芯片的中心频率则是透过ARM Cortex-M0芯片控制,以达到可任意选择带通模态的目的;其次,经过信号的整流与低通滤波过程,以进行振动模态信号的包络分析,为达到降低信号扭曲,对于信号整流过程采用精密全波整流电路。最终获得两个不同振动模态的包络信号,MAX274电路则如图4所示。

图3 轴承缺陷振动信号处理系统示意图
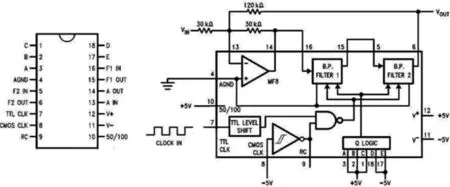
图4 MAX274电路图
3 实验分析
轴承最常见的缺陷分别为滚子缺陷、内环缺陷和外环缺陷,为模拟轴承运转时所会发生的缺陷情形,而利用放电加工将轴承各零件做表面的切割破坏,而各零件缺陷的尺寸大小如表1所示,由于缺陷部位不同,将对滚子缺陷、内环缺陷和外环缺陷分别进行研究。

表1 缺陷的尺寸数据
本研究选定3个共振模态进行实验分析,分别以两组模态进行相关系数分析比较,第1组为第一模态1k~3.5kHz与第二模态3.5k~6kHz,第2组为第二模态3.5k~6k与第三模态7k~9.5k,基于硬件电路的Filter法,求得各模态的包络信号,计算相关系数,同时比较其差异性,本实验选择800rpm、1600rpm和2400rpm转速来做实验分析,分别比较分析正常轴承和缺陷轴承在不同转速条件下,其相关系数的变化。
3.1 正常轴承
图5~图7为正常轴承的振动信号的模态解析结果,其中图5a、图6a与图7a为振动信号的全局频谱图,可发现在不同转速下的其全局频谱图,皆有相似的共振模态。图5b、图6b与图7b为时域的敲击信号,图5c~图5e、图6c~图6e与图7c~图7e看出正常轴承中的包络信号皆为随机信号。表2为正常轴承在三种转速下,基于Filter法与FFT法分别求得相关系数(50组实验数据的平均值)对照表;可知第一模态与第二模态的相关系数相较于第二模态与第三模态的相关系数要高,随着转速增加两组模态的相关系数也有稍微变大的趋势,但相关系数值皆小于0.1,轴承处于良好状态。
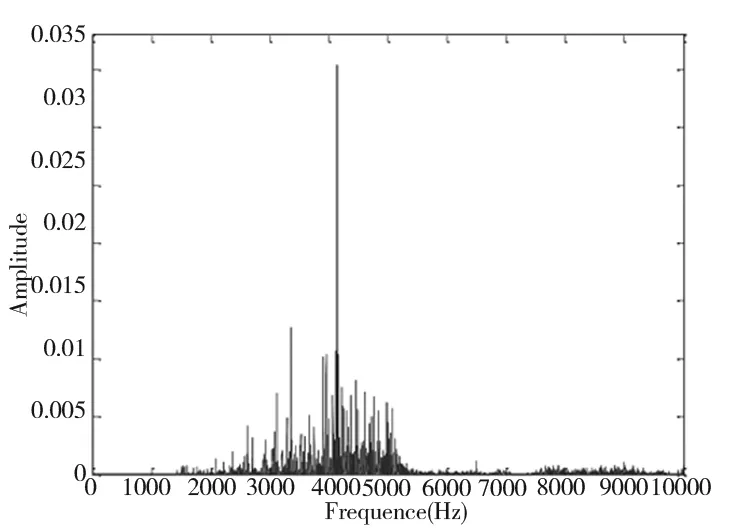
(a)全局频谱图

(b)时域的敲击信号

(c)第一模态的包络信号

(d)第二模态的包络信号

(e)第三模态的包络信号
(a)全局频谱图
(b)时域的敲击信号

(c)第一模态的包络信号

(d)第二模态的包络信号

(e)第三模态的包络信号
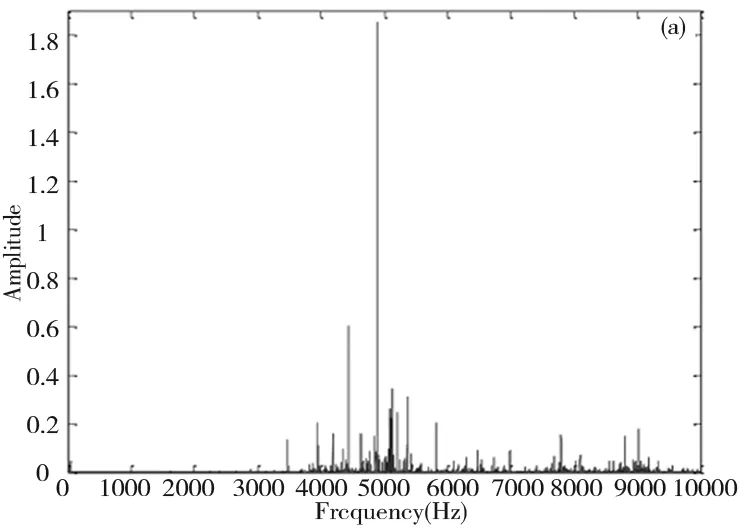
(a)全局频谱图

(b)时域的敲击信号

(c)第一模态的包络信号

(d)第二模态的包络信号

(e)第三模态的包络信号
3.2 滚子缺陷
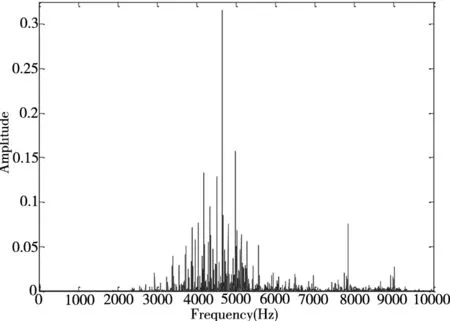
图8~图10为滚子缺陷的特性分析,图8b、图9b与图10b为时域的敲击信号,由图8c~图8 e、图9c~图9e与图10c~图10e看出三个振动模态的包络信号在滚子缺陷中皆有明显的变化。表3为滚子缺陷在三种转速下,基于Filter法与FFT法分别求得相关系数(50组实验数据的平均值)对照表;由表3可发现,在滚子缺陷相关系数值的变化趋势,第一模态与第二模态随着转速的增减,其相关系数并无太大的变化,而第二模态与第三模态随着转速上升,高频的能量也变高,相关系数有略微上升的趋势,两组模态的包络信号在各转速下,相关系数值皆大于0.5,与正常轴承的相关系数相比,两者差异较大。
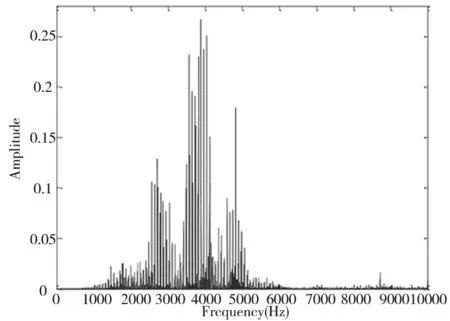
(a)全局频谱图

(b)时域的敲击信号

(c)第一模态的包络信号

(d)第二模态的包络信号

(e)第三模态的包络信号
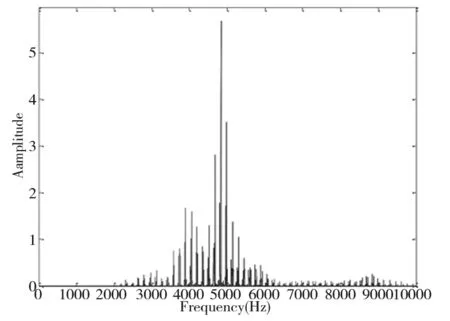
(a)全局频谱图
(b)时域的敲击信号

(c)第一模态的包络信号
(d)第二模态的包络信号
(e)第三模态的包络信号

(a)全局频谱图

(b)时域的敲击信号

(c)第一模态的包络信号

(d)第二模态的包络信号

(e)第三模态的包络信号
3.3 内外环缺陷
轴承转速在800rpm、1600rpm和2400rpm时,内外环缺陷包络信号与滚子缺陷类似,表4为内环缺陷轴承在三种转速下,基于Filter法与FFT法分别求得相关系数。可以看出应用Filter法诊断指标在第一模态与第二模态的相关系数,随着转速增加而略微降低;而在第二模态与第三模态的相关系数随着转速增加而略微上升,其整体相关系数变化起伏并无太大,两组模态的包络信号在各转速下的相关系数皆大于0.5。
表5为外环缺陷轴承在三种转速下的数据,可以看出,在第一模态与第二模态的相关系数值随着转速上升并无太大变化,由外环缺陷的特性可发现,无论转速的增减与否,外环缺陷在低频带的能量皆相当强;而第二模态与第三模态的相关系数值随着转速上升有略微上升的趋势,但外环的特性在高频带时能量略微较小,相关系数值所变化的幅度皆不大,但所求得的相关系数值皆大于0.4。
由各组缺陷轴承与正常轴承的相关系数实验结果得知,轴承缺陷诊断器能准确区别出正常轴承与缺陷轴承的差异,由表2~表5可以发现,在正常轴承与各类型缺陷轴承分别在三种转速下,第一模态与第二模态的相关系数值比第二模态与第三模态的相关系数值略高一些,随着转速的提高,相关性也会受到一定程度的影响,尤其是外环缺陷略微明显,从第三模态的包络信号可发现,外环缺陷随着转速提升,在高频带的能量依旧很小,而滚子缺陷与内环缺陷则是随着转速的提升,在高频带的能量也会跟着提升,但其对轴承缺陷整体的判断并无太大影响,但一样能明显地与正常轴承的相关系数做区别;由此规律,监测系统可以量化指标的方式呈现结果,基本可以设定相关系数(阀值)为0.4,当阀值小于0.4则轴承正常,反之,当阀值大于0.4时则轴承存在缺陷,并且能做实时监测,在缺陷发生时最短时间内判断轴承状况。
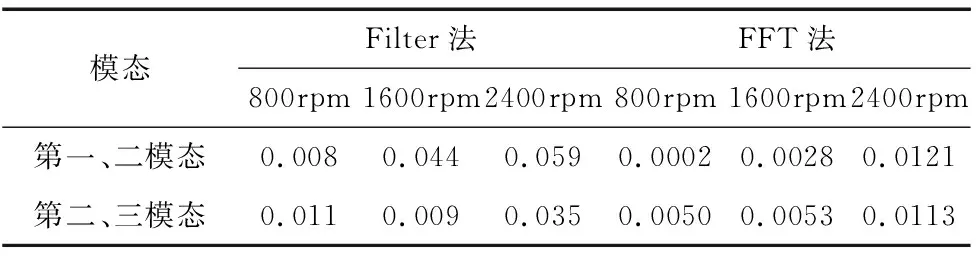
表2 正常轴承与各转速的相关系数表
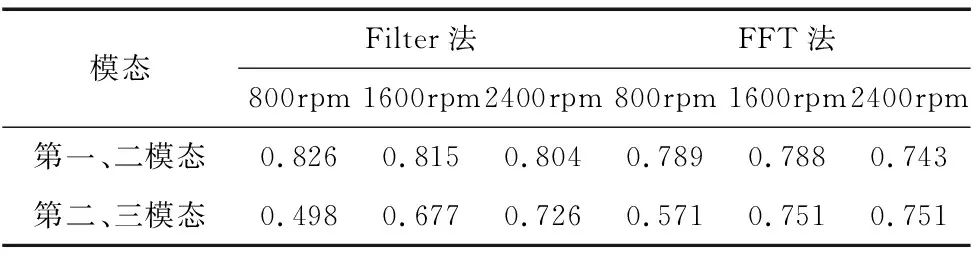
表3 滚子缺陷轴承与各转速的相关系数表
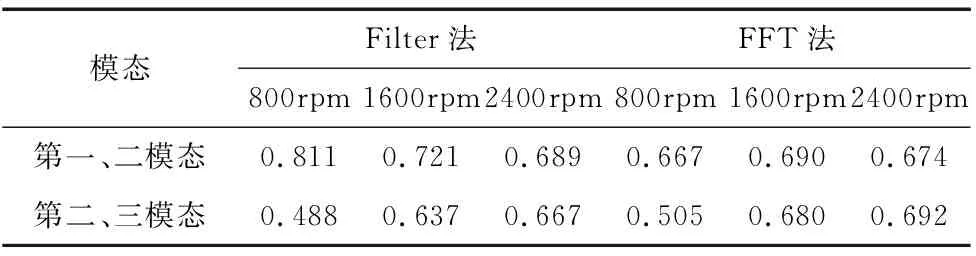
表4 内环缺陷轴承与各转速的相关系数表
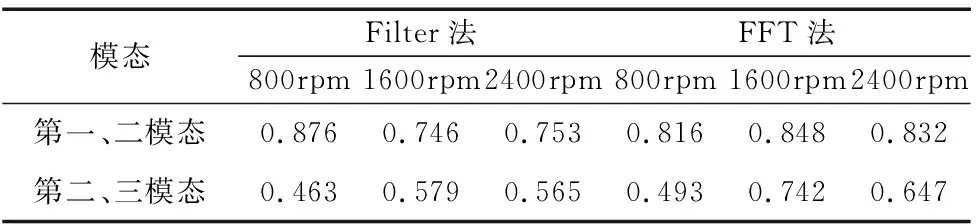
表5 外环缺陷轴承与各转速的相关系数表
4 结论
本文通过对轴承振动特性的研究,分析轴承振动信号中任意两种模态振动信号特性,利用Filter法对该振动模态信号进行调解分析,并计算出相关系数值,作为轴承缺陷监测系统的量化诊断指标。实验结果表明该系统通过设定阀值为0.4可以监测轴承是否存在缺陷,具有较强的准确性与实用性,为轴承缺陷实时监测提供了一种方便快速的方法,可以在实践中得以应用。
