基于自适应陷波器的伺服系统谐振抑制*

王昱忠，何 平，王志成，韩 旭

(1.中国科学院大学，北京 100049；2.中国科学院沈阳计算技术研究所高档数控国家工程研究中心，沈阳 110168；3.沈阳高精数控智能技术股份有限公司，沈阳 110168)

0 引言

在工业控制伺服系统中，电机与负载之间一般都是由齿轮、传动轴或者联轴器等传动装置进行连接，由于传动装置并不是完全刚性的，因此电机和负载之间存在柔性传动。柔性传动会引发机械谐振。

针对谐振的抑制问题，学者们已经提出了许多相应的解决办法。传统的PID[1]法其参数整定繁琐，且自适应较差。利用观测器[2-3]来抑制谐振的方法，其参数是通过离线调节获取的，不适合在线谐振抑制。陷波滤波法[4-6]需要高效的谐振频谱辨识方法来准确辨识谐振频率，传统的FFT不能满足需求。文献[7-8]采用自适应陷波滤波器设计方案，该方案能够辨识伺服系统的谐振中心频率，并以此频率来调整设计陷波滤波器，但其也有辨识速度慢的问题。先进控制算法的应用包括滑膜变结构控制[9]、H∞[10]控制。高级算法运算复杂、计算量大，在当前伺服驱动系统中受硬件条件的影响难以真正推广使用。

本文提出了一种基于改进的FFT在线频率检测法结合陷波滤波器的自适应谐振抑制策略。通过提取旋转因子的公因子来减少内存的读取次数，进而提高FFT的频域分析速率。并且设计了一种获取陷波器宽度、深度参数的方法。利用得到的陷波频率、宽度、深度参数设计陷波滤波器。具有陷波深度的三参数陷波滤波器弥补了传统二参数陷波滤波器的不足，提高了陷波滤波的性能及精确度。

1 机械共振产生的机理分析

在伺服电机驱动负载运行的过程中，电机与负载可以被简化为一个二惯量系统模型，二惯性系统模型通常都会发生机械谐振现象。 二惯量系统模型如图1所示。

图1 二惯量系统模型

在图1中，Jm、Jl、Tm、Tl、Ks分别为伺服电机的惯性矩、负载端的惯性矩、电机转矩、扰动转矩和传动轴的弹性系数。ωm、θm和ωl、θl分别为电机和负载的转速和旋转角度。当伺服系统的传动装置发生扭转形变时其轴端将产生转矩Tw。建立如下方程：

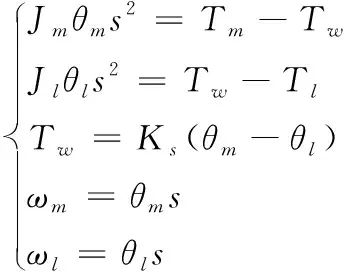
(1)

由式(1)可以推导出电机转矩与电机转速之间的传递函数关系，具体表示为式(2)：

(2)

由式(2)推导出式(3)：

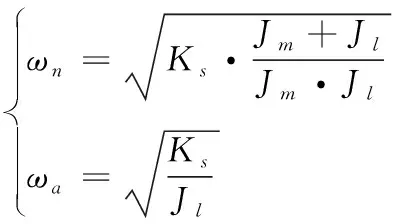
(3)

从式(3)可知，伺服系统中引入了谐振频率点ωn和反谐振频率点ωa。谐振频率点的存在使得伺服系统在该频率下的响应会变得比较强烈，这就会形成机械谐振现象。

2 谐振频率的在线检测

由于伺服系统发生机械谐振会引发电机转速及转矩的振荡。因此对转速误差进行改进的FFT分析能直接反应系统中存在的机械谐振现象。谐振的在线检测框图如图2所示。

图2 谐振在线检测框图

2.1 频谱分析算法FFT

在实际的数字控制系统中，对连续的转速误差信号进行离散化采样，采样结果的长度为N的非周期序列，用FFT法进行频谱分析。其主要包括蝶形运算与码位倒读两部分。

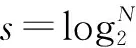
2.2 谐振频率提取算法的设计

对电机转速误差信号经过改进的FFT变换后，其结果数据以复数R(n)=a+bi形式存储在缓冲器中。分析FFT运算结果，设计算法来提取谐振频率。首先计算出R(n)频率的幅值|R(n)|，若|R(n)|值大于阈值Hset，则视该值为有效幅值，否则视为无效的噪声。如果|R(n-1)|满足如下条件：|R(n)|>|R(n-1)|；|R(n)|>|R(n+1)|和|R(n)|>Temp，就将|R(n)|的值存储在临时数据寄存器Temp中，就进入下一次循环，直到n=N退出循环为止，算法结束。

此时，Temp中存储R(n)和对应的点数n。其流程框图如图3所示。

图3 频率提取算法流程图

若采样频率为fs，采样点数为N，从而得出谐振频率为：f=(n-1)×fs/N。

3 陷波滤波器的设计

3.1 陷波滤波器特性分析

传统的陷波滤波器传递函数如式(4)所示：

(4)

在此二阶陷波滤波器传递函数中，ωn为陷波作用频率点，合理的设计即可消除伺服系统的谐振峰值；同时还可以通过调节参数k来调整陷波滤波器的陷波带宽；但是不能调节陷波的深度。为了能准确方便地对陷波滤波器的中心频率、陷波带宽及陷波深度进行调节，本文将选择运用改进型的双T陷波滤波器来进行谐振抑制。其传递函数如公式(5)所示：

(5)

该陷波滤波器的幅频响应特性如图4所示，陷波滤波器在谐振频率ωn处的幅值增益AG和带宽Bω分别为:

(6)

(7)

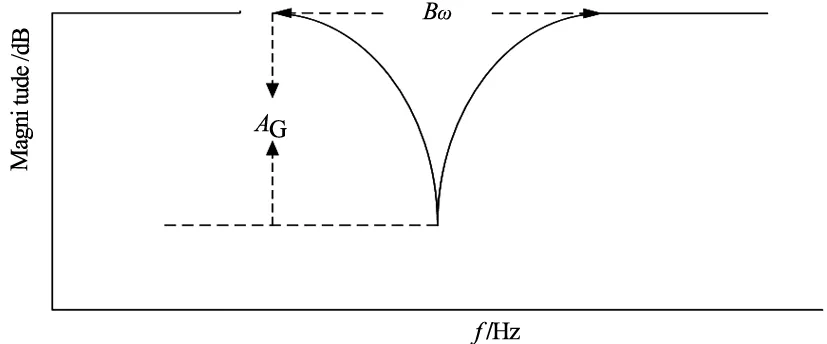
图4 陷波滤波器的幅频响应

3.2 陷波滤波器的参数确定

采用陷波滤波器，通过适当调整滤波器参数，可以有效地抑制机械振动，包括谐振频率，幅值和带宽。所以要确定陷波器的3个参数ωn、k1、k2是谐振抑制模块的一个重要任务。

通过图5进行分析设置。

图5 FFT频谱分析曲线

(1)陷波滤波器的谐振频率很容易确定，它只是对应于FFT分析曲线最高点的频率。前面谐振的在线检测已经得出，可以表示为如下：

f=ωn

(8)

(2)在所设计的陷波滤波器的作用下，幅值应衰减到给定的阈值。假设阈值为Hset，其中Hset

Bω=2max{(ωn-ω1),(ω2-ωn)}

(9)

由于阈值的设置与FFT采样的大小有一定的关系，需要一定的工程经验。在后面的实验中，我们使用1024点来进行FFT频谱分析并设置阈值Hset为200。

(3)深度参数代表陷波中心频率处的凹陷程度，并且在知道参数Hset和Hmax之后，为了保持一定的余量，可以通过如下表达式来表示：

(10)

α一般设置为0.7～0.9之间，本文设置α为0.8。通过上面的分析，由式(7)～式(10)可确定参数ωn、k1和k2。

(4)由于实际伺服驱动系统均是数字化控制系统，因此陷波滤波器必须在应用之前进行离散化，利用差分方程来设计陷波器，差分方程如式(11)所示:

(11)

由于设计的陷波器是二阶的，陷波滤波器差分方程的系数长度为三，将差分方程展开如式(12)所示：

y(n)=b0x(n)+b1x(n-1)+b2x(n-2)-a1y(n-1)-a2y(n-2)

(12)

其对应的离散系数如下：

(13)

其中,T为采样周期。

4 实验设计与验证

4.1 整体结构设计

本文提出了一种基于自适应陷波器的伺服系统谐振抑制方案。总体结构如图6所示。

基于自适应陷波器的伺服系统谐振方案主要包括数据采样、FFT频谱分析、谐振频率提取、陷波滤波器的参数确定4步完成。开启谐振抑制功能后，开始采样转速误差信号。在每一个采样周期内系统将完成一次数据采样，同时把每次采集的数据完整的存储到寄存器中。当采样的点数达到预定的点数时，采样结束并开始进行FFT 频谱分析运算，对FFT分析的结果采用频率提取算法获取谐振频率点。通过获取的谐振频率点和后面确定的陷波带宽、陷波深度参数一起来设计合理的陷波滤波器，以此来抑制谐振。

根据香农采样定理，采样频率应大于信号频率的2 倍，测量频率的范围为0～500Hz，再考虑到分辨率与采样频率的关系，因此，设置采样频率为1 kHz，采样点数为1024点。本文中每个周期采样3组1024点数据存入数据缓冲阵列，是为了抑制改变速度基准的影响。对于FFT的分析结果，可以根据参考变化的影响来检测和拒绝谐振频率。

4.2 实验结果

机械谐振抑制平台实物照片如图7所示。实验所采用的DSP芯片为TMS320F28335芯片。采用CCS6作为开发工具，电机为沈阳高精数控生产的GJM010ADA2S永磁同步电机，额定功率为1.5kW，转矩为7.5N·m，额定转速为1000r/min，额定电流为5.8A，额定电压2000V。

图7 实验装置图

采样频率为1 kHz，对1024个采样点进行频谱分析如图8所示，从图中可以看出谐振频率为240Hz。

图8 FFT频谱分析

如图9所示，系统达到给定的转速后，电机转速发生持续的震荡，这是发生机械谐振所引起的现象。在0.8s时投入自适应陷波滤波器，经过0.5s转速的振荡得到衰减，系统的谐振得到很好的抑制。

图9 基于自适应陷波器的谐振抑制实验波形

5 结论

针对伺服系统中机械传动装置刚度有限所引发的机械谐振问题，提出了基于改进的FFT在线频率检测法结合陷波滤波器的自适应谐振抑制策略。通过提取旋转因子的公因子来减少内存的读取次数，进而提高FFT的频域分析速率，使系统的速度振荡在0.5s内得到了衰减。文中设计了一种获取陷波器宽度、深度参数的方法，弥补了传统无深度参数陷波滤波器的不足，提高了陷波滤波的性能及精确度。