6-UPS正交并联机构运动学分析与研究

王清运，刘 勇，徐志刚，尹 猛,2，靳阳阳

(1.中国科学院沈阳自动化研究所, 沈阳 110016；2.中国科学院大学,北京 100049；3.东北大学 机械工程与自动化学院, 沈阳 110819)

0 引言

随着科学技术的发展,在精密机械仪器、材料科学、航空航天设备等领域中,对高精度、高分辨率多自由度的姿态调整机构需要越来越多。并联机构具有结构紧凑、运动链短、刚度高和承载能力大等优点,在大载荷风洞天平测试过程中,占据着绝大的优势。复位机构是大载荷风洞天平测试的主要机构，因此并联机构是复位机构调姿的理想机构原型,受到了国内外学者的高度重视。

国内外学者对并联机构的运动学、动力学、误差分析等相关方面做了深入的研究，并联机构的运动学分析依然是研究的重要环节[1]。文献[2-4]对Stewart平台进行了运动学建模与仿真分析，针对正解、逆解、动力学等方面进行了研究，文献[5]对三自由度4-SPS/CU并联机构进行了运动学和工作空间分析；文献[6]对具有6自由度的4-UPS-UPU并联机床进行了详细的研究，构建了运动学模型并对灵巧度进行了分析；文献[7]对5自由度5-UPS-PRPU并联机床进行了运动学分析，文献[8]提出了一种新型4-SPS/PPU并联机构，对机构的运动学进行了速度、加速度理论分析。

本文通过对风洞天平校准布局及末端姿态的调整要求，设计了一种新型复位机构,介绍其主体结构和布局特点,对其建立运动学模型，推导出其位置正反解方程，通过Adams软件的仿真结果对数值解析进行验证，对机构的设计具有重要的意义。

1 6-UPS并联机构模型

复位机构为正交解耦的6自由度并联平台，它是通过Stewart平台变异得到的新型机构。复位机构包含有运动平台1和6个UPS运动链2和基座3。其中，UPS运动链通过6分支二力杆结构进行三个方向的复合驱动，与传统6自由度stewart平台比较，具有耦合少及控制精度高等优点，具体原理结构如图1所示。其中垂向分3点布置3套二力驱动杆、轴向布置1套二力驱动杆及侧向布置2套二力驱动杆，二力杆底部与支撑座连接，顶部与运动平台连接，通过6套二力驱动杆的伸缩运动实现平台的6自由度调整运动。

1.运动平台 2.UPS运动支链 3.基座图1 复位机构的三维结构图

1.1 运动链布置方式

运动链的布置方式采用正交分布的形式进行布置，其主要由1个X向运动链分支、2个Y向运动链分支、3个Z向运动链分支和运动平台组成。其中，X向运动链分支与基座轴系的X向平行；Y向运动链分支与基座轴系的Y向平行，且两侧对称布置；Z向加载分支有3个，基座轴系的Z向平行，呈等腰三角形布置。复位机构的运动链分支布置形式采用3-2-1的布置方式，如图2所示。机构工作时，根据各个运动支链的杆长变化来调整运动平台的位姿。

图2 复位机构运动链分支的布置形式简图

1.2 自由度分析

根据Chebyshev-Grubler-Kutzbach(CGK)公式，空间自由度[6]的计算：

2 运动学分析

2.1 运动学建模

6自由度复位机构固接的参考坐标系记为{P}：O′-x′y′z′，原点O′位于运动平台球铰点理想位置分布圆的中心。在参考坐标系{P}中，与6自由度复位机构相连的铰链点Bi的空间位置用矢量PBi(i= 1,2...6)表示。地基固接的绝对坐标系记为{Q}：O-xyz，原点O在下铰链圆周圆心上，如图3所示。6自由度复位机构上铰链在绝对坐标系{Q}中其空间位置矢量用QBi(i= 1,2...6)表示，与地基连接的铰链中心在绝对坐标系{Q}其空间位置矢量用QAi(i= 1,2...6)表示。

图3 复位机构的建模图

根据各个球绞具体分布位置，现有运动平台Y向两球绞之间的距离为a，X向两球绞之间的距离为b，Z向球绞位置为底边距离为e。在绝对坐标系{Q}：O-xyz建立各上下铰链的空间位置矢量，来描述各个铰链在空间位置的坐标。

2.2 运动学逆解

QBi和QAi分别表示在绝对坐标系{Q}空间位置矢量，表示为：

PBi表示在参考坐标系{P}中上铰链的空间位置矢量，表示为：

在绝对坐标系{Q}与参考坐标系{P}的坐标系变换过程中，由空间坐标变换理论可得如下关系：

QBi=TPBi+R

其中，R为参考坐标系{P}原点(既上平台中心)在绝对坐标系{Q}中的位置矢量，T为3×3旋转变换矩阵，由于转角α、β、γ足够小，使sinα→α，sinβ→β，sinγ→γ，cosα→1 ，cosβ→1，cosγ→1，旋转变换矩阵T可写为：

上下铰链在坐标系中的位置矢量已表示出来，高精度电动缸长度矢量Li可由几何结构矢量关系表示：

进而求矩阵：

|Li| = |QBi-QAi|

设各驱动缸的长度用li(i=1,2,...,6)表示，则下式为并联机构的位置反解。

2.3 数值解析分析

由以上分析可知，在该并联机构的末端位置和姿态已知的情况下，机构参数也是已知的，则6条支链的杆长伸缩量就很容易得出。现有尺寸在模型中测量有a=1160mm,b=1340mm,e=2250mm。

研究6自由度正交并联机构如图3所示，可见上下平台参考坐标系，其中每个铰链点在各自坐标系中的坐标参数如表1所示。

表1 6-UPS机构上、下铰链坐标参数

续表

随机取三组位姿样本，求得相应杆长，动平台的位姿参数如表2所示。

表2 6-UPS机构动平台位姿参数

通过逆解模型及表2给定的位姿样本，可求得上述长度的参数，如表3所示。

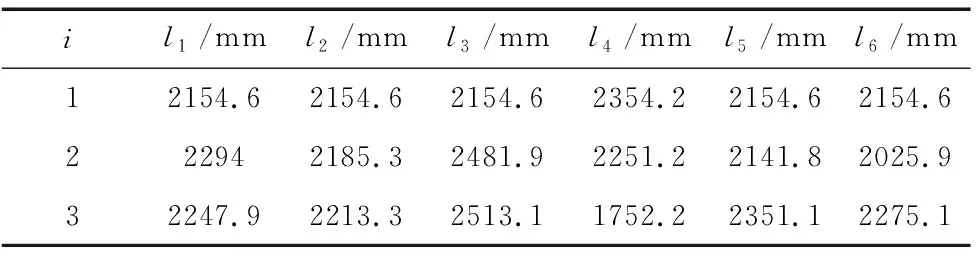
表3 各杆长的长度参数

3 运动学正解

现有6个杆共同控制运动平台来完成其运动，各杆的杆长参数为L=(L1,L2,L3,L4,L5,L6)，动平台中心位姿为Q，记为：

其中，x,y,z表示为位置矢量，α、β、γ表示其姿态矢量。

3.1 基于最小二乘法的正解分析

由于方程是非线性方程，直接得到末端方程正解值比较困难。为了得到方程的正解值，采用最小二乘法迭代的方法进行非线性方程组的求解。

最小二乘法的非线性方程组的求解步骤：

x∈R,并以任意初始值开始迭代的一个解x1;

(2)构造迭代方程式，从一个解x1开始迭代，产生一系列的{xk}将收敛到一个周期点xj：

(3)选取xj的任意邻域中选取大量不同点作为最小二乘法迭代方法的初始点，变可得到非线性方程的解。

为了求解并联机构的正解值，将方程组转化为标准方程形式：

表4 并联机构动平台输出位姿参数

通过这3组验证算例发现，相对来说，位置和姿态都有一定的误差，但是误差符合预期，在理想范围。同时，结果表明最小二乘法对非线性方程组的求解具有可行性和正确性。

3.2 机构工作空间的分析

并联机构工作空间结构运动形式较多，受各个驱动杆长影响较大，在运动学方程及运动约束方程基础上，以6-UPS复位机构为研究对象，采用蒙特卡罗法对动平台的工作空间进行分析，其原理式为:

W={ω(q):q∈Q}⊂R3

式中，w为工作空间；q为驱动关节变量；ω(q)为广义关节变量函数；Q为驱动空间；R3为三维空间。

蒙特卡洛法求解运动平台工作空间主要步骤：

(1)通过给定每个杆长的设计变量的随机值；

(2)求正交并联机构的运动学正解表达式，从而得到运动平台末端位置值在绝对坐标系中的表示；

(3)通过MATLAB软件作图，绘制绝对坐标系中的所有末端点的位置，从而生成机构工作空间点的云图。

现给定6个杆长的运动变化范围:

采用MATLAB软件计算运动平台中心位姿的工作空间进行仿真，为使6-UPS复位机构的工作空间能够清晰地描绘出来，取N为20000点，结果显示的工作空间仿真云图，如图4所示。

图4 6-UPS工作空间仿真云图

4 运动学仿真验证

要使并联机构的运动平台有较好的运动情况，就需要在各个杆上添加相应的驱动，来验证运动学模型的正确性。利用SolidWorks建立6-UPS并联机构模型，将模型导入到Adams软件中，添加相应的约束和驱动，完成虚拟样机的搭建。

在Adams软件中，在杆间与基座相连的虎克绞关节处定义并添加虎克约束，在各个电动缸与缸桶之间定义并添加移动约束，在前端的球绞和运动平台之间定义并添加球绞约束。6-UPS并联机构的虚拟样机模型如图5所示。

图5 6-UPS正交并联机构虚拟样机模型

4.1 运动学逆解仿真

现对6-UPS并联机构的中心点Q施加一个点驱动，将其驱动函数设置成正弦函数，来观察6杆的杆长变化情况，点驱动函数表达式如下所示。

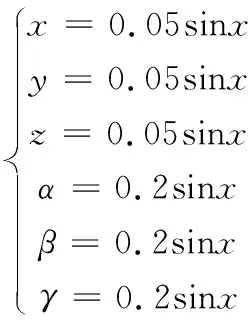
将系统的仿真时间设置为10s,观察每个杆长的运动情况。仿真结果如图6所示。

图6 各杆长的变化曲线

由图6可知，在运动过程中，各杆长分支的伸缩量随时间变化的曲线平稳、光滑，每个杆都有其运动范围，为设计复位机构确定驱动杆长提供了参考意义。

4.2 运动学正解仿真

现对6-UPS复位机构的6个杆施加移动驱动，将其驱动函数设置成正弦函数，来观察末端位置和角速度的变化情况情况，移动驱动函数表达式如下所示：

将运动的仿真时间设置为10s,运动平台的运动仿真结果如图7～图10所示。

图7 运动平台的X向位移

图8 运动平台的Y向位移

图9 运动平台的Z向位移

图10 运动平台的X、Y、Z向角速度变化

图7～图10的结果可以知道：复位机构的运动过程中，运动平台的位移和角速度随时间变化的各个曲线有一定的运动，具有实现六自由度调整姿态的能力，且无尖点和凸起，运动过程无冲击，机构的运动符合要求。

5 结论

(1)为解决复位机构的高精度以及较大的承载刚度的问题，设计了一种并联形式的复位机构，提高了复位机构的承载能力。该机构采取3-2-1的正交布置方式，提高了复位机构的运动精度，对复位机构的设计提供了参考。

(2)对机构的运动学进行分析以及仿真验证，说明复位机构在实际运动时具有可行性和运动的协调性好，能够满足复位机构的运动要求。

(3)通过Adams的仿真研究，对6-UPS正交并联复位机构进行了运动学仿真，获得了驱动分支伸缩变化量与运动平台位姿之间的关系曲线，对复位机构通过杆长驱动量来控制位置姿态有着重要的意义。