自由曲面铣削表面形貌仿真方法研究*
2019-01-23周晓勤谢雪范孙厚野
周晓勤,谢雪范,马 伟,孙厚野,薛 迪,吴 凯
(1.吉林大学 机械科学与工程学院,长春 130025;2.北京航星机器制造有限公司,北京 100013)
0 引言
自由曲面广泛应用于航空航天、光学元件、汽车、船舶及模具等领域[1],其主要功能的实现不仅取决于几何设计,而且也依赖于加工质量,如光学元件表面加工寄生的纳/微尺度波纹或残高,会对其色散系数造成较大的影响,继而恶化其成像质量[2]。因此,通过表面形貌仿真进行加工质量控制和工艺参数优化对于自由曲面元件设计及加工极具现实意义,其研究受到国内外研究人员的广泛关注。
近年来,针对球头铣刀铣削表面形貌的仿真研究已经取得了长足的进展,例如,A Antoniadis等[3]通过将球头铣刀刀刃和加工表面离散,然后运用Z-map法获得平面铣削的三维几何形貌,并开发出表面形貌仿真软件。S Ehsan Layegh K等[4]通过沿进给方向截取进给速度矢量的垂直面,并分析该垂直面内不同切削行刀刃摆线运动投影,以此建立平面铣削表面形貌仿真模型。W H Zhang[5]、谭刚[6]等使用牛顿迭代法解非线性方程组生成球头铣刀铣削平面和圆柱面的表面形貌。常树禹[7]从刀具切削形成的包络面出发,基于Biharmonic样条曲面插值方法获得平面铣削表面形貌仿真模型,该方法可避免Z-map法运算效率低的缺点,但仿真精度难于控制。从现已报道的相关文献看,针对平面和柱面等简单面形的铣削表面形貌仿真,无论是理论方法还是技术手段均已十分成熟。
然而,目前针对自由曲面等复杂表面铣削加工的三维形貌仿真鲜有报道,究其原因,自由曲面的加工轨迹通常难以在时域内建立运动方程并准确描述,但建立任意切削时刻与刀位点位置之间的映射关系又是表面形貌仿真必不可少的环节。针对该问题,彭芳瑜[8]、赵厚伟[9]等通过计算刀具每次插补运动中进给速度的三向分量(fx,fy,fz),建立刀位点的三向运动方程并求解刀位点位置,这种方法是有效的,但考虑到加工轨迹是逼近自由曲线的折线段,这种方法计算冗杂,不利于编程实现。文章旨在提出新方法,能够简洁地表达任意切削时刻与刀位点位置之间的映射关系,以便于实现诸如自由曲面这类复杂曲面表面形貌仿真。
1 自由曲面铣削表面形貌建模
1.1 工件模型
如图1所示,以理想加工表面上任意一点为原点建立工件坐标系{Ow;Xw,Yw,Zw},在XwOwYw平面内设置仿真区域并按仿真精度要求划分网格,而后将网格沿Zw向投影至工件待加工表面,生成工件的Z-map模型。仿真时,以二维数组H(x,y)保存加工表面上任意点(x,y)对应的z坐标,切削过程中H(x,y)不断更新,并以最终的H(x,y)和对应的x、y坐标为特征点生成加工表面的三维形貌[10]。H(x,y)初始化为轴向切深。
1.2 刀刃扫掠点模型
为清楚地表达刀具相对工件的运动以及考虑到主轴回转误差,如图2所示,使用工件坐标系、刀具坐标系{Ot;Xt,Yt,Zt}及主轴坐标系{Os;Xs,Ys,Zs}来确定任意时刻、任意刀刃微元在工件坐标系内的坐标。
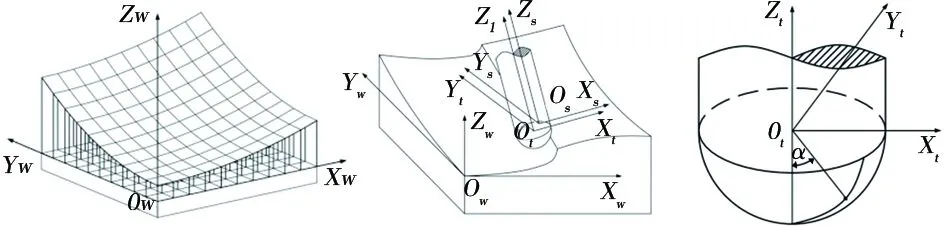
图1 工件的 Z-map模型 图2 铣削运动 坐标系 图3 刀刃微元 示意图
从运动学角度分析表面形貌的形成过程,是参与切削的刀刃与工件发生相对运动从而去除工件材料,并由加工表面残留材料形成表面形貌。刀刃不同部位切削残留量显然不同,因此需要分析每一个刀刃微元相对工件的运动情况。如图3所示,刀具坐标系内任意切削时刻t,∠α所表征的刀刃微元坐标,需要经过坐标变换,映射到工件坐标系内,变换过程如式(1)所示。
(1)
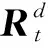
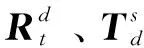
(2)
(3)
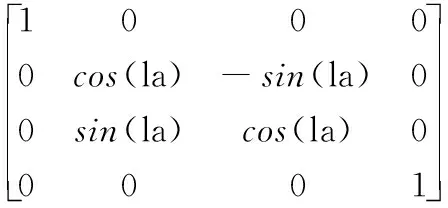
(4)
式(3)中,Δdr为主轴回转偏心误差;Δα1为主轴回转偏心初相;Δda为轴向窜动误差;Δα2为轴向窜动初相。
式(4)中,la为主轴坐标系绕工件坐标系Xw轴的旋转角度;ta为主轴坐标系绕Yw轴的旋转角度,{x(t),y(t),z(t)}表示t时刻对应的刀位点位置。
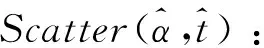
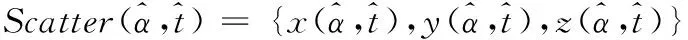
(5)
1.3 刀位点位置检索算法
由1.2节可知,t时刻对应的刀位点位置{x(t),y(t),z(t)}实质上描述了刀位点刀具轨迹信息,因此如何获取{x(t),y(t),z(t)}就成为建立刀刃扫掠点模型的关键点和难点。一般的解决方法是根据规划刀位点建立三向运动方程描述刀具轨迹,但由于刀位点须密集规划,插补运动的速度矢量方向不断变化,导致运动方程非常繁杂,不利于计算机编程求解。基于上述基本情况,文章提出了一种矢量检索算法用于获取t时刻对应的刀位点位置,其核心思想是将铣刀在相邻刀位点间的直线插补视为一个进给矢量,并记录每个矢量的起终点时刻及位置信息,而后通过检索记录,找出任意给出的切削时刻t相对应的进给矢量,进而计算出该时刻所对应的刀位点位置。仿真前,须提前规划加工表面的刀具轨迹并提取出离散的刀位点。
记一次进给过程中的qm个按加工时间排序的刀位点构成的空间点集为矩阵A,A中的第q行元素表示第q个刀位点,并用Aq表示;记t时刻对应的目标刀位点位置为Q={x(t),y(t),z(t)};算法的具体步骤如下:
Step1:输入刀位点矩阵A、时刻t及进给速度vf;
Step2:初始化刀位点循环变量q=1、插补起始时刻循环变量tst=0及行循环变量r=1;计算A中刀位点的数目qm;初始化记录矩阵B;
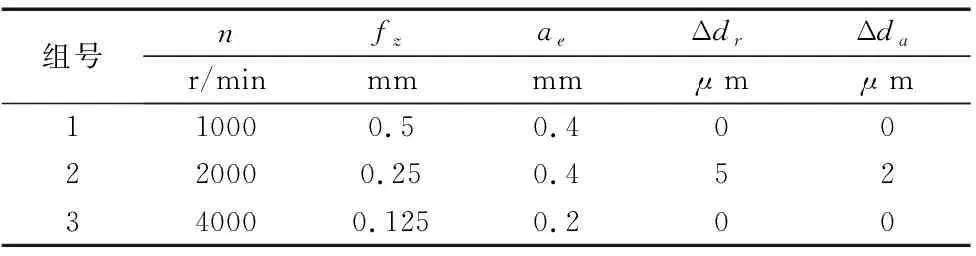
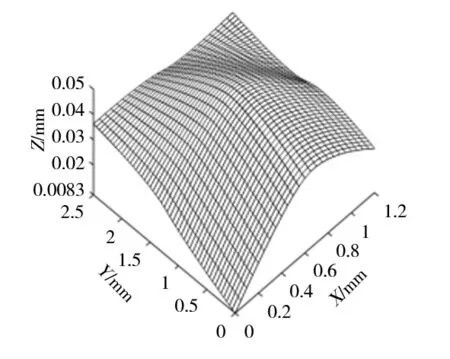
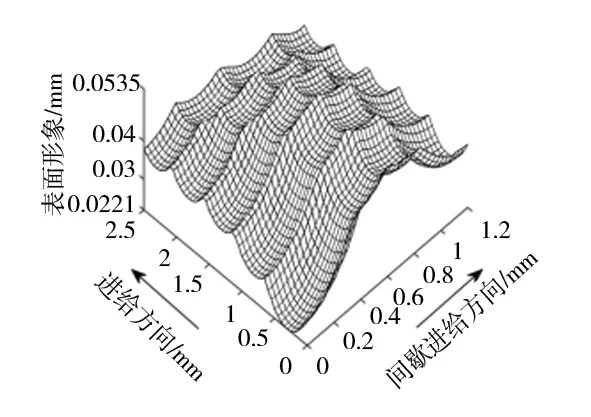
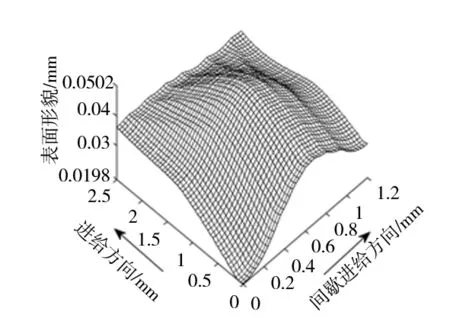
Step3:刀位点循环终止条件判断(q Step4:计算由刀位点Aq指向刀位点Aq+1的矢量模长l、单位方向向量ve,并按等式ten=tst+l/vf计算刀位点Aq+1对应的插补终止时刻ten,而后将刀位点Aq、Aq+1对应的坐标信息Qst、Qen及ve、tst、ten作为一行元素存储于记录矩阵B中; Step5:tst=ten;q=q+1;重复Step3; Step6:插补起始时刻循环终止;刀位点循环终止; Step7:调用矩阵B、刀位点的数目qm; Step8:行循环终止条件判断(r Step9:寻的条件判断(tst≤t≤ten);若判断为真,则执行Step10,否则执行Step11; Step10:行循环终止,取tst、ten所在行的Qst及ve,按等式Q=Qst+ve(t-tst)计算并输出Q; Step11:r=r+1;重复Step7; Step12:行循环终止,输出“t不在当前进给切削时间范围内”; 至此,使用上述算法可获得仿真所需的{x(t),y(t),z(t)}。 获取工件模型及刀刃扫掠点模型后,就可以使用Z-map法[11],以近似替代的方式求出工件模型与刀刃扫掠点模型的逻辑交点,并完成二维数组H(x,y)的更新,获得三维表面形貌。 为验证上述方法,在MATLAB中生成非均匀有理B样条曲面(Non-Uniform Rational B-Spline, NURBS)作为设计的自由曲面,按上述方法步骤进行铣削表面形貌仿真。NURBS曲面的控制点阵CP如式(6)所示,相应的权因子阵为4×4单位阵,U向和V向阶次均为3。 (6) 式中,x1=-0.1;x2=0.4;x3=0.8;x4=1.3;y1=-0.2;y2=0.8;y3=1.6;y4=3。 铣削仿真中,加工参数设置如表1所示。 表1 加工参数 仿真时表1中全部测试组加工倾角均为30°,轴向切深为0.3mm,且均采取单向行切、顺铣加工方式。球头铣刀直径为10mm,2刃,螺旋角30°(右旋)。设计曲面如图4所示,第1~3组参数的仿真结果分别如图5~图7所示。 观察对比仿真结果,测试组1、2进给量较大,因此输出形貌反映出明显的球头铣刀铣削加工纹理特征;而测试组3进给量较小,加工残留高度极小,输出形貌比较接近设计曲面,与实际加工经验相符,证明上述检索算法能够应用于表面形貌仿真。 图4 设计曲面 图5 测试组1的输出形貌 图6 测试组2的输出形貌 图7 测试组3的输出形貌 文章提出了一种描述切削刃相对运动的新方法,它不需要建立切削时间与刀位点位置之间具体的函数表达式,而是根据刀具的插补运动,以矢量检索算法求出任意切削时刻对应的刀位点位置。与建立三向运动方程的一般方法相比,该方法将对三个方向的运动方程求解替换为对特定单一进给矢量的检索,简化了计算过程,利于计算机编程实现。经仿真实例检验,以这种新算法为基础所建立的表面形貌仿真模型是合理有效的,可以用于自由曲面表面形貌几何仿真。1.4 生成表面形貌
2 仿真实例


3 结论
