采用牺牲层技术的电容式微机械超声传感器的仿真与分析

郭 庆 李 妍 高 尚 张培玉

(河南大学物理与电子学院，河南 开封 475000)

引言

超声被广泛应用于人类社会的许多领域，包括医学成像、无损检测和超声处理、工业清洗等。自从Curie兄弟在1 880年发现压电传感器中的压电效应以来[1]，压电换能器得到了很大的发展。从20世纪40年代开始，压电换能器就一直占据着主导地位[2-4]。然而，由于阻抗不匹配等原因，使得压电换能器在空气和液体中的应用受到很大的限制[5-6]，并且压电材料的微加工工艺也限制了电容式微超声传感器(CMUT)的工作频率范围[7-8]。

随着MEMS技术的发展,催生了电容式微超声传感器[9-10]。在超声成像领域，与占有统治地位的压电超声传感器相比，CMUT具有很多优点，展现出即将取代压电传感器之势。超声传感器是能把电能转换成声能或将声能转换为电能的装置，由于采用微加工技术，较好地克服了压电换能器的许多缺点[11]，并且使微小尺寸结构(包括CMUT单元)和结构中电容间隙即使在亚微米范围内，也很容易实现[12-13]。

为了更好地研究CMUT，许多研究人员建立了CMUT模型来模拟CMUT的特性[14-15]。以往大都研究单一的CMUT单元，大多数的分析模型是基于文献 [16-18] 提出的数学理论构建的。早期的数学仿真模型可用来描述由于偏置直流电压作用下膜的静态偏移[17]，该模型将CMUT近似为一个弹簧质量块的一阶系统。这一模型可以定性地说明CMUT一些特性，但是对于CMUT特性的定量分析还是显得过于简单。之后，文献[18-20]提出的模型更为接近实际CMUT结构。

CMUT建模是CMUT研究的重要组成部分。以往的研究建模多聚焦在CMUT的本身结构上，而甚少考虑微加工方法的影响。通常，CMUT的加工工艺主要有采用牺牲层释放技术和采用键合等工艺加工，但以往的CMUT模型甚少把CMUT的加工方法考虑进去。

本研究试图通过考虑以牺牲层技术工艺方法加工的CMUT来构建CMUT模型。众所周知，这在以往的CMUT模型中是前所未有的。本研究在考虑牺牲层释放法的影响的基础上，提出了4个CMUT模型，即矩形薄膜CMUT模型、CMUT的BOX模型、含有释放孔的CMUT模型和含有释放通道的CMUT模型，并对4种CMUT模型进行分析对比。

1 方法

CMUTs一般是由多个电容传感器单元组成，各个单元的空间区域的有效利用对CMUTs的功率的影响和对空间的利用率的影响是显而易见的。所以，CMUT单元的形状是影响CMUTs功能的一个不可忽略的问题。

CMUT的振动薄膜可以采用多种形状，包括圆形、正方形、长方形和正六边形等。由于圆形振动薄膜结构为轴对称结构，易于分析、仿真和加工。以往的研究中大都是对圆形薄膜结构进行分析，鲜有其他薄膜结构[21-22 ]。但是，由于圆形结构的面积利用率较低,本研究基于以前对CMUT的研究[7,8,21]可知，矩形薄膜的填充系数高，即单位面积上的有效传感器表面面积高。所以，本研究采用的CMUT的振动薄膜为矩形结构。在考虑牺牲层释放技术的基础上，构造4种CMUT的物理模型，采用大型工程有限元分析软件ANSYS，对物理模型进行有限元建模并仿真。其中，传感器结构采用3D元素SOLID45构建结构单元，传感器腔体为静电和结构耦合场，采用SOLID226构建传感器腔体结构单元，来完成仿真传感器的共振频率等性能参数。

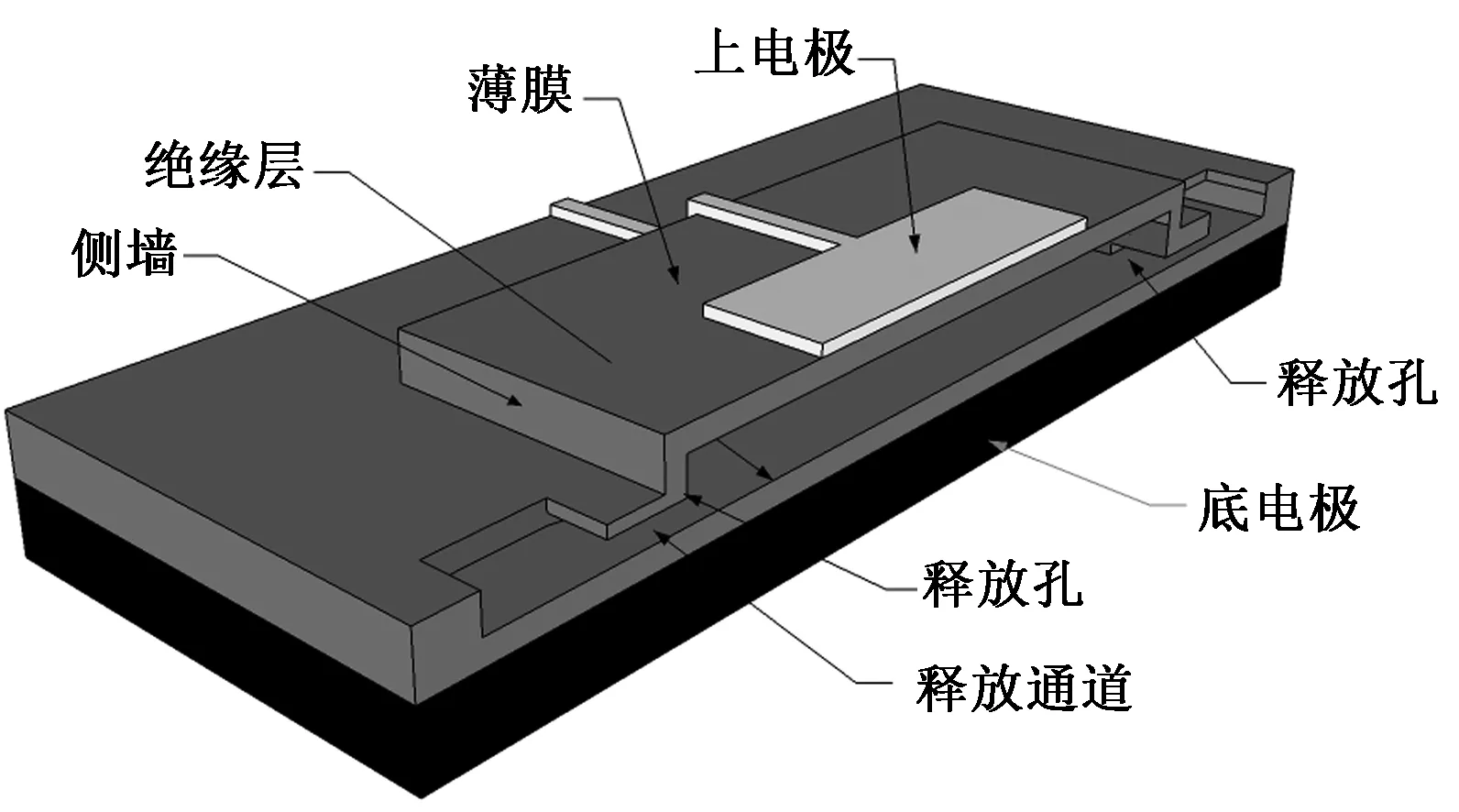
图1 CMUT结构剖视图Fig.1 The sectional view of CMUT

图1是一个典型的采用牺牲层释放方法加工的矩形振动薄膜结构的CMUT结构剖视图，其工艺过程可参见文献[22-23]。其基本结构是一对平行板电容器结构，包括一个固定的底电极，一个对应的弹性薄膜和居积在其上的上电极，上部电极和底电极之间有绝缘层。其中，弹性薄膜用来传输和(或)接收来自邻近介质的声波，完成传输和接收声波信号。薄膜下为空腔，空腔的形成是通过采用牺牲层技术获得[21]。为形成空腔，需要有释放孔和释放通道，如图1所示。图1所示的结构可简化为由弹簧、质量块和电容3个部分组成的简单的平行板电容器模型。该模型是建立在以下3个方面的简化：一是薄膜的弹性恢复力是线性的，并且是薄膜位移的函数；二是该模型工作在真空中，且导体的接触都是理想的；三是忽略边缘电场和薄膜的曲率问题。

当CMUT被施加电压时，平行板电容器的上薄膜在静电力的作用下发生变形，电压增大，变形增大。当系统处于平衡状态下，有

Fm=Fe+Fk

(1)

式中，Fm为薄膜的重量，Fe为电容器的静电力，Fk为弹簧的回复力。

而静电力为

(2)

式中，ε为薄膜材料的介电常数，S为电容两极板的相对面积，V为电容器两级板间电压，tg为两极板间的距离，x为薄膜极板的位移。

薄膜的弹性恢复力为

Fk=-kx

(3)

式中，k为薄膜的弹性系数。

由式(1)～(3)可得

(4)

式中，m为薄膜的质量。

如果仅施加直流偏压，薄膜位移与时间历程无关，则

(5)

当直流偏压增大到某一数值时，继续增加会使薄膜受到的静电力大于弹性回复力，此时薄膜会出现吸合现象。吸合电压为

式中，Vpull-in为吸合电压，xpull-in为薄膜的极限位移。

共振频率f0为

(8)

式中，A为薄膜变形系数(与薄膜的长宽比有关)，h为薄膜厚度，a为薄膜的边长，E为薄膜材料的弹性模量，ρ为材料的密度。

为了探讨结构的变化对CMUT性能尤其是共振频率的影响，构建的CMUT模型包括矩形薄膜CMUT模型(见图2)、BOX模型(见图3)、含释放孔的CMUT模型(见图4)和含释放通道的CMUT模型(见图5)。在本研究中，采用大型有限元仿真软件ANSYS分析CMUT的结构参数，包括振动薄膜的厚度、边长和长宽比、空腔间隙、腐蚀释放孔的参数等对CMUT共振频率的影响。

图2展示了最简单的单个矩形薄膜CMUT模型。该模型主要由矩形振动薄膜、 空腔间隙、 绝缘层和底电极构成，上电极在薄膜之上(图中没有标出)。此模型是以前研究的用牺牲层释放法加工的电容式微机械超声传感器采用的模型[8]。在静电力的作用下，振动薄膜被吸引，引起薄膜变形，从而引起上下电极间的电容发生变化。振动薄膜的约束为四周施加固定约束，薄膜采用20节点结构体单元(SOLID45)进行有限元构建。该模型同样适用于采用键合技术加工的CMUT。表1列出了CMUT单元结构的几何参数以及它们的变化范围。

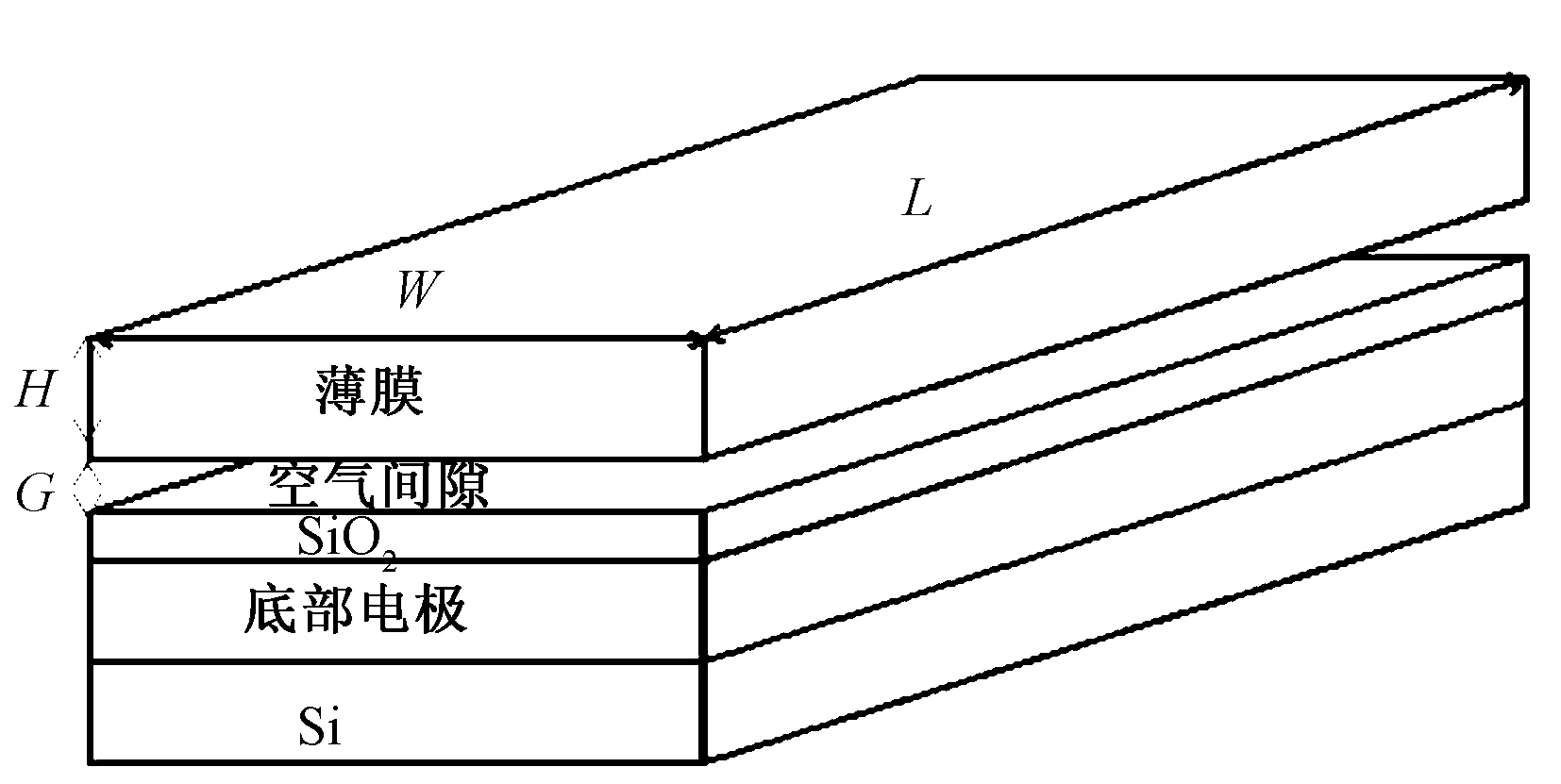
图2 CMUT矩形薄膜模型Fig.2 The block-shape membrane model of CMUT

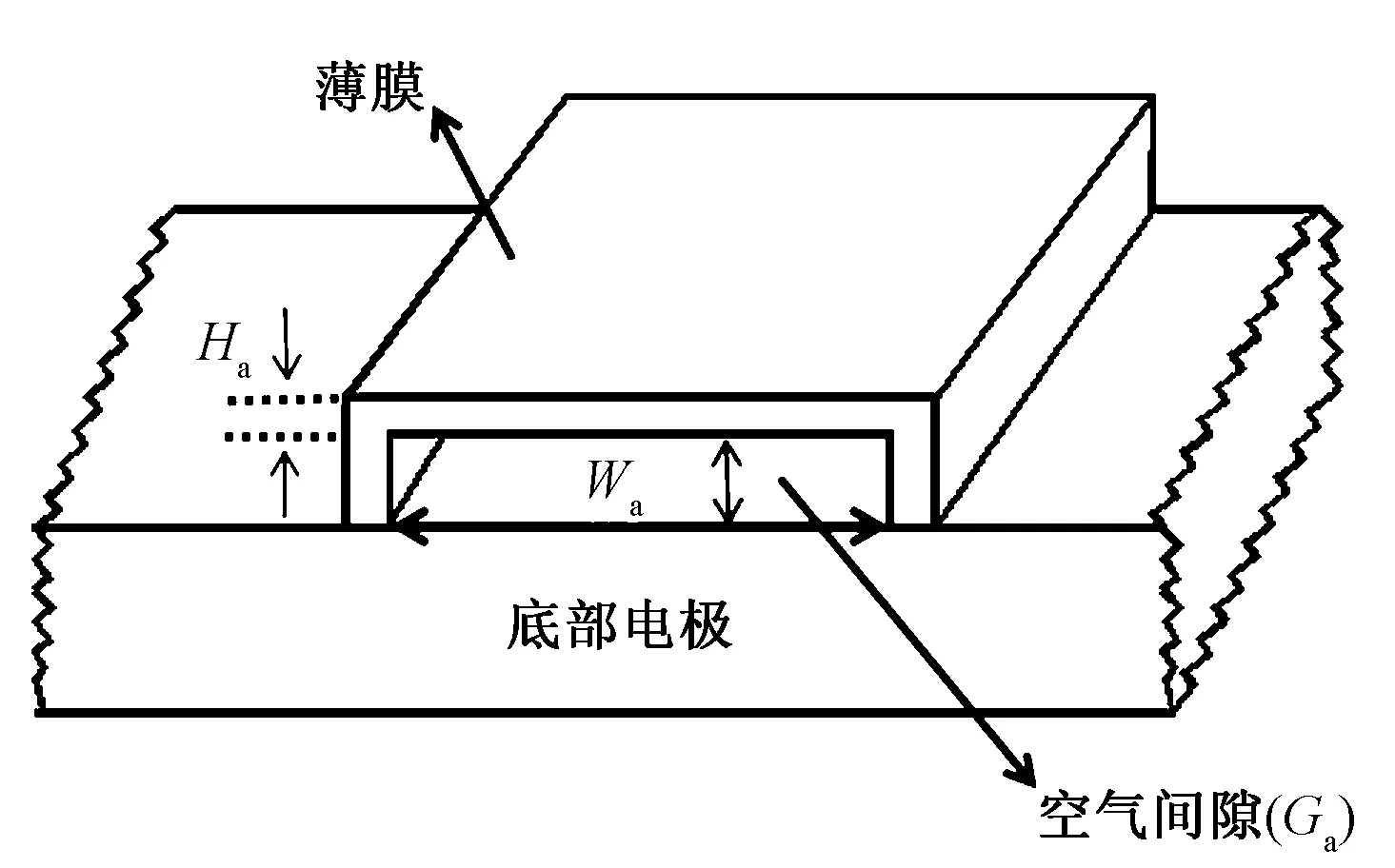
图3 CMUT的BOX模型Fig.3 The BOX model of CMUT

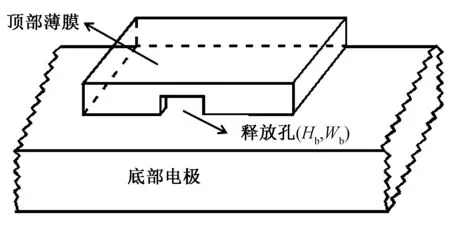
图4 含有释放孔的CMUT模型Fig.4 The model of CMUT with etching holes

图5 含有释放通道的CMUT模型Fig.5 The model of CMUT with etching channels

表1 矩形薄膜CMUT的结构参数Tab.1 The parameters block-shape membrane model

CMUT单元工作时，当振动薄膜的振动频率接近结构的固有频率时，振动薄膜的振幅达到最大，无论是输出功率还是引起电容的变化均达到极值。所以，分析时，将CMUT的工作频率设定为结构的共振频率，一般为一阶共振频率。

在采用牺牲层释放法加工CMUT时，采用矩形薄膜构建CMUT的模型，计算分析简单。但由于释放结构形成的薄膜支撑结构也是弹性结构，所以，在第1种CMUT模型的基础上，考虑加工方法的影响，构建了第2种CMUT结构：BOX模型，如图3所示。该模型在第一种模型的基础上，增加了四周的支撑墙，与采用牺牲层释放法加工的CMUT单元结构近似。表2列出了BOX模型的CMUT单元结构相关几何参数的值和变化范围。

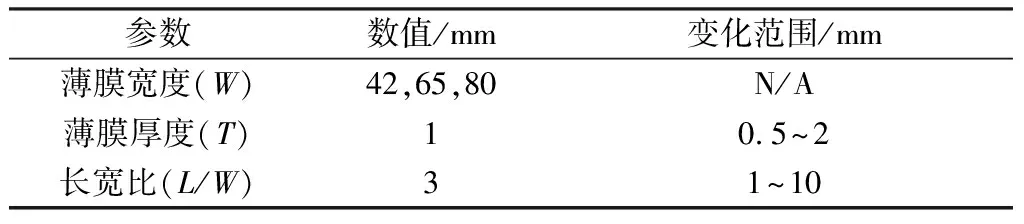
表2 CMUT的BOX模型的结构参数Tab.2 The parameters of BOX model for CMU

图3为CMUT的BOX模型的剖视图，是矩形薄膜CMUT模型的进一步改进。分析仿真时，薄膜四周的支撑墙的底部采用固定约束。通过对薄膜底部四周施加约束，来对结构进行有限元仿真，分析薄膜厚度以及薄膜长宽比的变化对CMUT性能的影响。CMUT的BOX模型的结构接近实际的结构。然而，遗憾的是，由于牺牲层释放法加工的结构均需要牺牲层材料的释放孔。所以，为了使CMUT模型接近实际CMUT结构，在BOX模型的基础上，第3种CMUT模型是在BOX模型的支撑墙上增加刻蚀孔或称释放孔。图4所示为一个含有释放孔的CMUT模型，表3列出了含有释放孔的CMUT模型单元结构相关的结构参数。

表3含有释放孔的CMUT模型的相关结构参数

Tab.3TheparametersofCMUs’modelwithetchingholes

参数数值/mm变化范围/mm空腔高度/Ga1N/A释放孔的宽度/Hb20Ga/6^5×Ga/6释放孔的高度/Wb0.5W/10^W

考虑释放孔的CMUT模型与BOX模型相比，削弱了CMUT结构的刚度。实际加工过程还需要有蚀刻通道完成牺牲层材料的释放。所以，在考虑释放孔的CMUT模型的基础上，增加释放通道，形成含有释放通道的CMUT模型。建模方法与前述类似，其结构模型如图5所示。表4列出了含有释放通道的CMUT模型单元结构相关的结构参数。

表4含有释放通道的CMUT模型的相关结构参数

Tab.4TheparametersofCMUs′modelwithetchingchannels

参数数值/μm变化范围/μm空腔高度/Ga1N/A释放孔/释放通道的宽度/Hb20Ga/6^5×Ga/6释放孔/释放通道的高度/Wb0.5W/10^W

为验证有限元模型的仿真结果，搭建了实验平台，采用激光测振仪(microsystem analyzer MSA-500, Polytec Inc., Irvine, CA, US)测试超声传感器的共振频率。实验所用的电容式微机械超声传感器是通过采用牺牲层释放法，加工出的超声传感器[24]。其结构参数为振动薄膜边长80 μm，厚度为1 μm。

2 结果

通过对建立的CMUT等4种模型的仿真，得出如下结果。

2.1 矩形薄膜CMUT模型的仿真结果

薄膜厚度是影响矩形结构的CMUT共振频率的一个主要因素。图6显示不同薄膜厚度的矩形薄膜各阶共振频率的变化。在其他参数保持不变的情况下，对比显示可以看出，当膜厚度增加时，共振频率也逐渐变大。

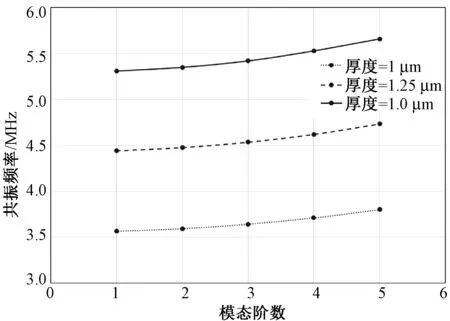
图6 薄膜厚度与共振频率的关系Fig.6 The relationship between thickness vs. resonant frequency

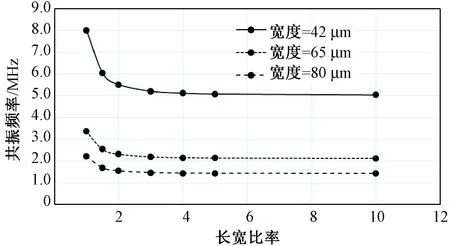
图7 薄膜长宽比与共振频率的关系Fig.7 The relationship between L/W vs. resonant frequency

薄膜的长宽比(L/W)是影响矩形结构共振频率的另外一个关键参数。共振频率和长宽比之间的关系如图7所示。在这里仿真了3种不同宽度的矩形薄膜CMUT之间随薄膜长宽比的变化对共振频率的影响。

3种矩形单元的共振频率随长宽比的增加逐渐降低，当长宽比>4时，基本不再发生变化。

2.2 CMUT的BOX模型的仿真结果

很明显，矩形薄膜CMUT模型和BOX模型的主要区别是结构的刚性条件发生了变化。笔者分别对二者进行了仿真，并对结果进行了比较分析。

分析薄膜厚度的影响时，假定CMUT其他结构参数保持不变。薄膜厚度的变化范围为0.5～2.0 μm，薄膜厚度随共振频率的变化以及两者的百分比误差如图8所示。

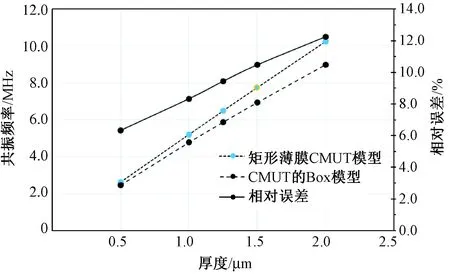
图8 薄膜厚度与共振频率的关系及误差Fig.8 The relationship between the thickness vs. resonant frequency

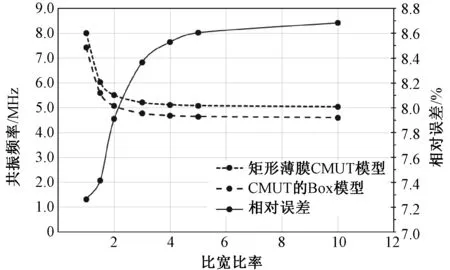
图9 薄膜长宽比与共振频率的关系及误差Fig.9 The relationship between the ratio of L/W vs. resonant Frequency

同样，分析薄膜长宽比的影响时，假定CMUT的其他结构参数保持。将薄膜的长宽比率从1增长到10，共振频率的变化以及两者的百分比误差如图7所示。

如图8所示，随着薄膜厚度的增加二者共振频率同样增加，百分比误差也逐渐变大。

图9显示了两者在长宽比变化的情况下，共振频率变化趋势基本一致，并且随着长宽比的增加两者之间的百分比误差也逐渐变大，当长宽比近似等于1时，得到最小的7.26%的差异，当长宽比等于5时百分比差异上升到8.7%。随后，变化趋于平缓。

2.3 含有释放孔的CMUT模型的仿真结果

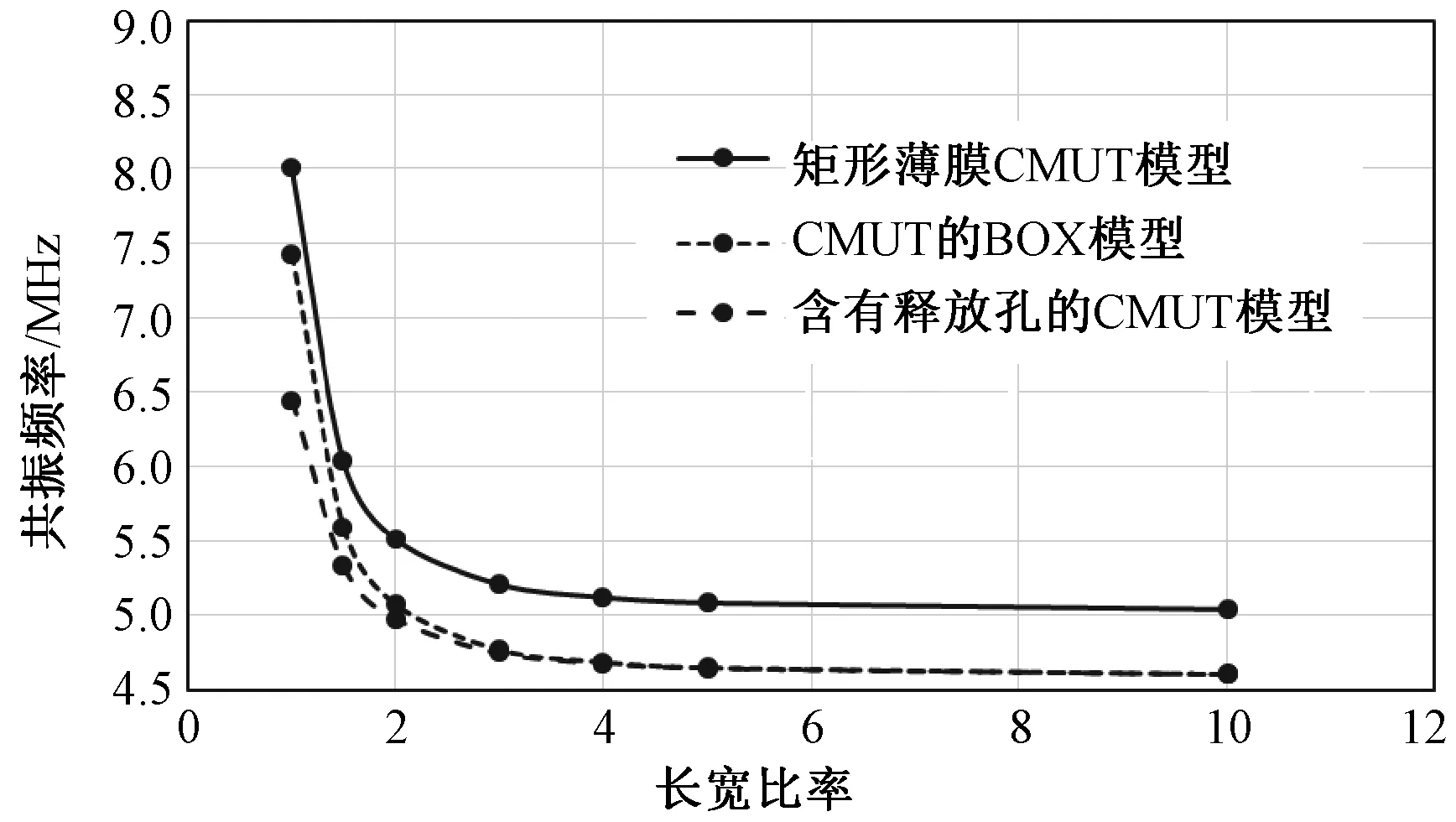
图10 3种CMUT模型仿真结果的比较Fig.10 Property′s comparison of three CMUTs′ models

与上面的分析过程类似，比较3种结构在不同薄膜长宽比的条件下共振频率的变化趋势，以及三者之间的百分比误差，如图10、11所示。如图10所示，三者之间的变化趋势基本一致，当薄膜长宽比>4后基本不再变化。从图11可以看出，含有释放孔的CMUT模型与BOX模型在长宽比>4时，两者之间对共振频率的影响基本没有差别，但是它与矩形薄膜的CMUT模型的最小差异为8.7%。

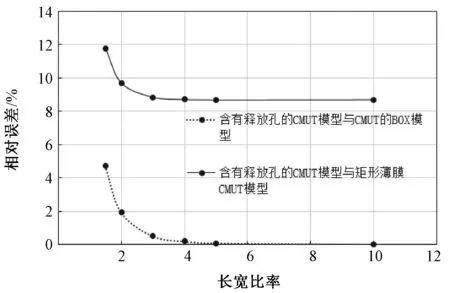
图11 3种CMUT模型相对误差比较Fig.11 The error comparison of three CMUTs’ models

2.4 含有释放通道的CMUT模型的仿真结果

4种不同模型中，长宽比的变化引起CMUT性能变化的曲线如图12所示。由图13可知，矩形薄膜CMUT模型与后3个CMUT模型的仿真结果相差较大。但随薄膜长宽比变化的趋势基本一致。当薄膜的长宽比>4时，后3个CMUT模型的仿真结果基本一致。

为了更直观比较，采用柱形图对4种CMUT模型的仿真结果进行对比。薄膜的厚度从0.5 μm增加到2.0 μm，4种CMUT模型结构的共振频率与振动薄膜的厚度的关系柱状图如图14所示。

为了能给CMUT实际微加工的工艺结构设计提供参考，对释放通道的结构变化(主要包括宽度和高度)进行更细致的研究。在保证薄膜长、宽尺寸以及空腔高度不变的情况下，通过改变释放通道与薄膜宽度的比率以及释放通道与空腔的高度的比率来实现对CMUT特性的影响分析。

在这里将含有释放孔的CMUT与含有释放通道的CMUT进行联合分析，在其他参数保持不变的情况下，释放通道的宽度Wb与薄膜的宽度W之间的比率从从1/6～5/6变化，图15为释放孔的宽度变化引起传感器的共振频率变化曲线。

将空腔的宽度Ga与释放通道的高度Hb之间的比率从1～10变化，图16中观察到随高度比变化引起传感器共振频率变化的曲线，以及两种结构之间的百分比误差。因为含有释放孔和释放通道的模型的仿真结果较为接近，图16的纵向坐标的单位数值保留小数点后两位有效数字。

从图15中可以看出，当宽度比增加时，结构的共振频率会下降，两种结构的百分比误差逐渐增加，当宽度比达到5/6时，两种结构之间的百分比误差最大，达到0.33%。

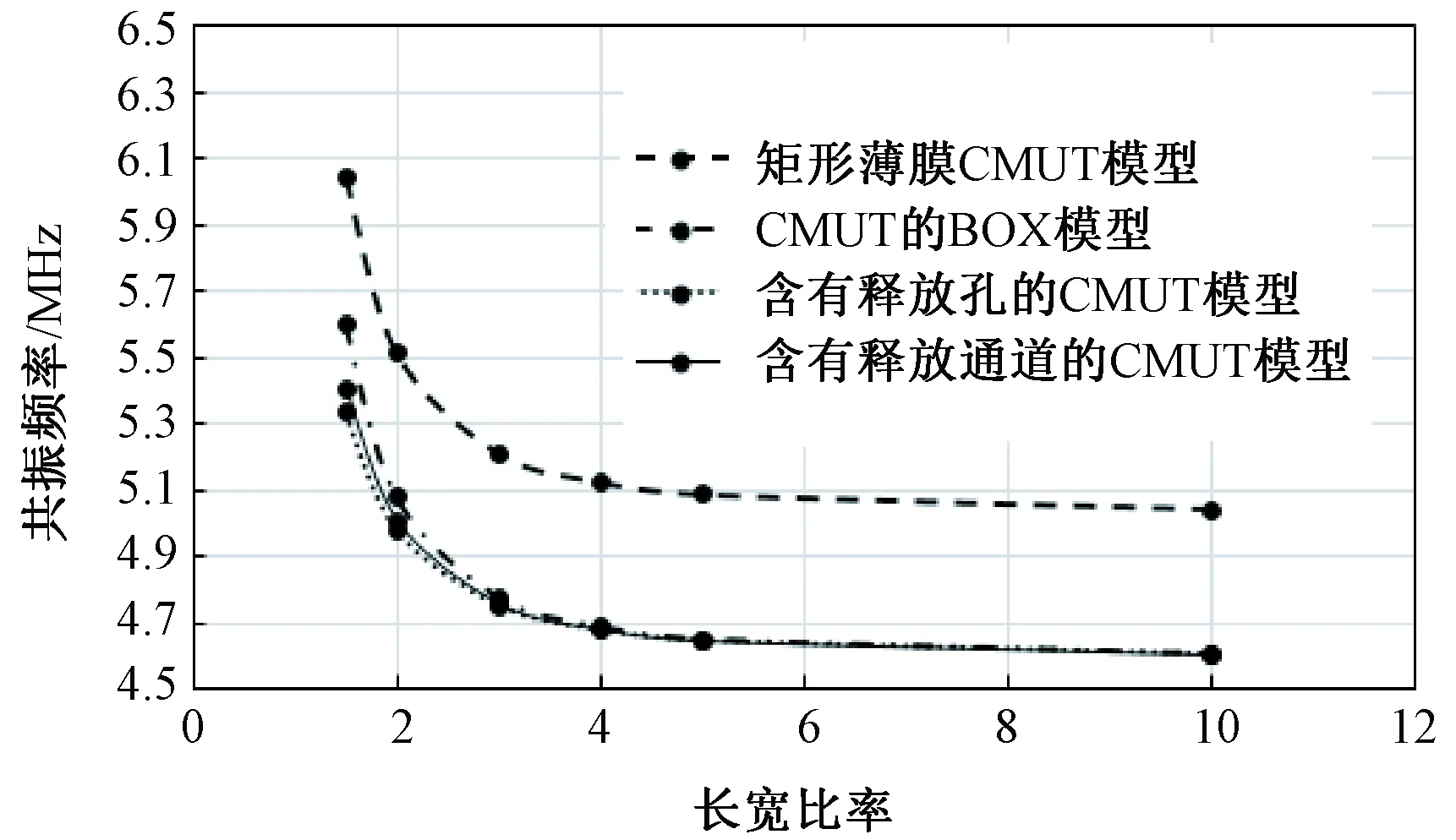
图12 4种CMUT模型仿真结果的比较Fig.12 Property′s comparison of four CMUTs′ models

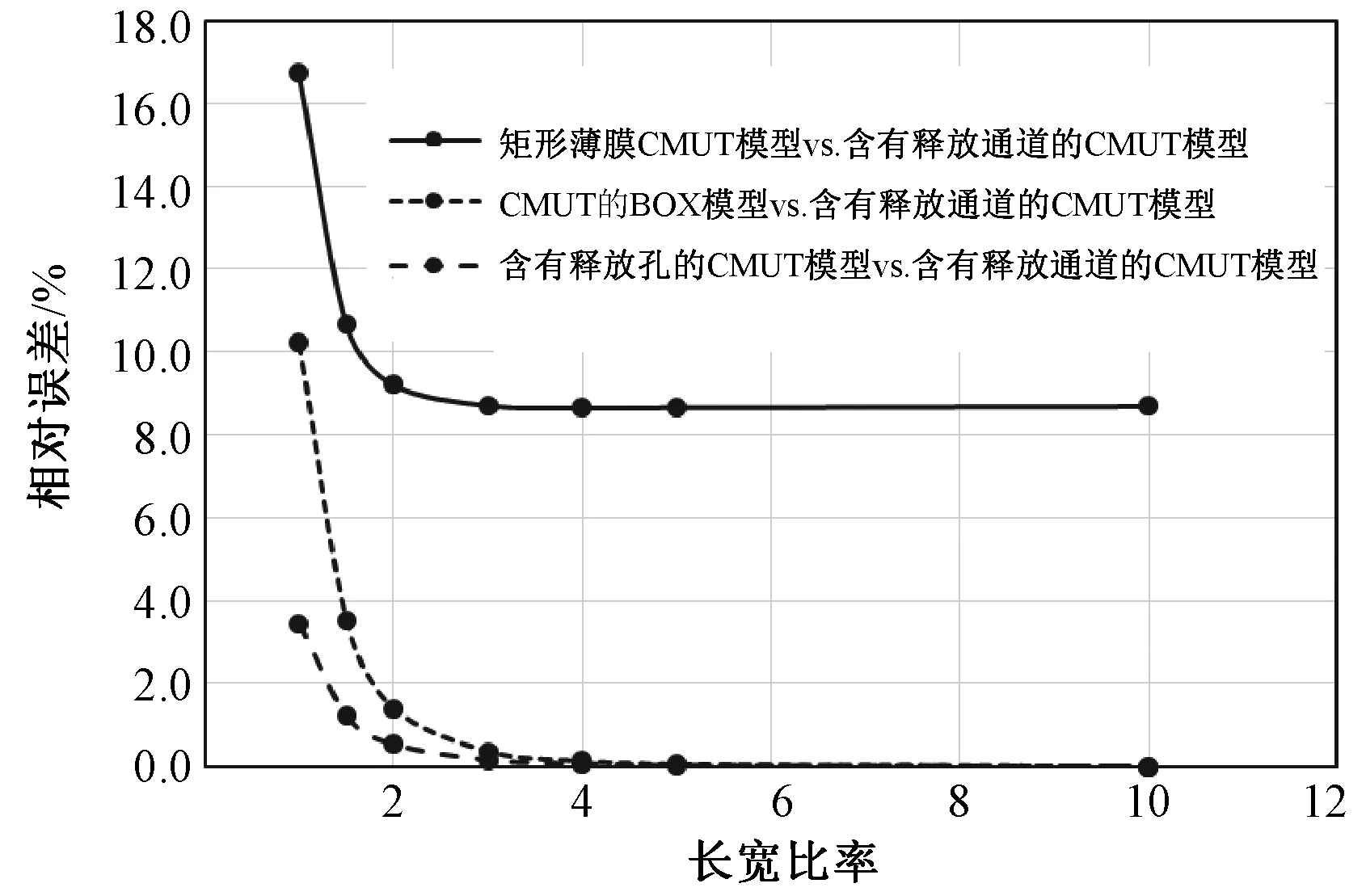
图13 4种CMUT模型仿真结果的比较Fig.13 Property′s comparison of four CMUTs′ models

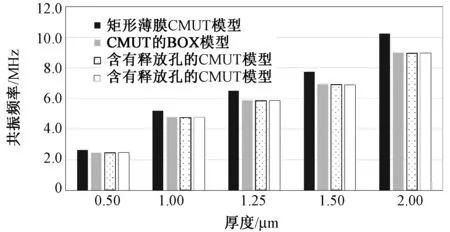
图14 薄膜厚度与共振频率的关系Fig.14 The relationship between the thickness vs. resonant frequency

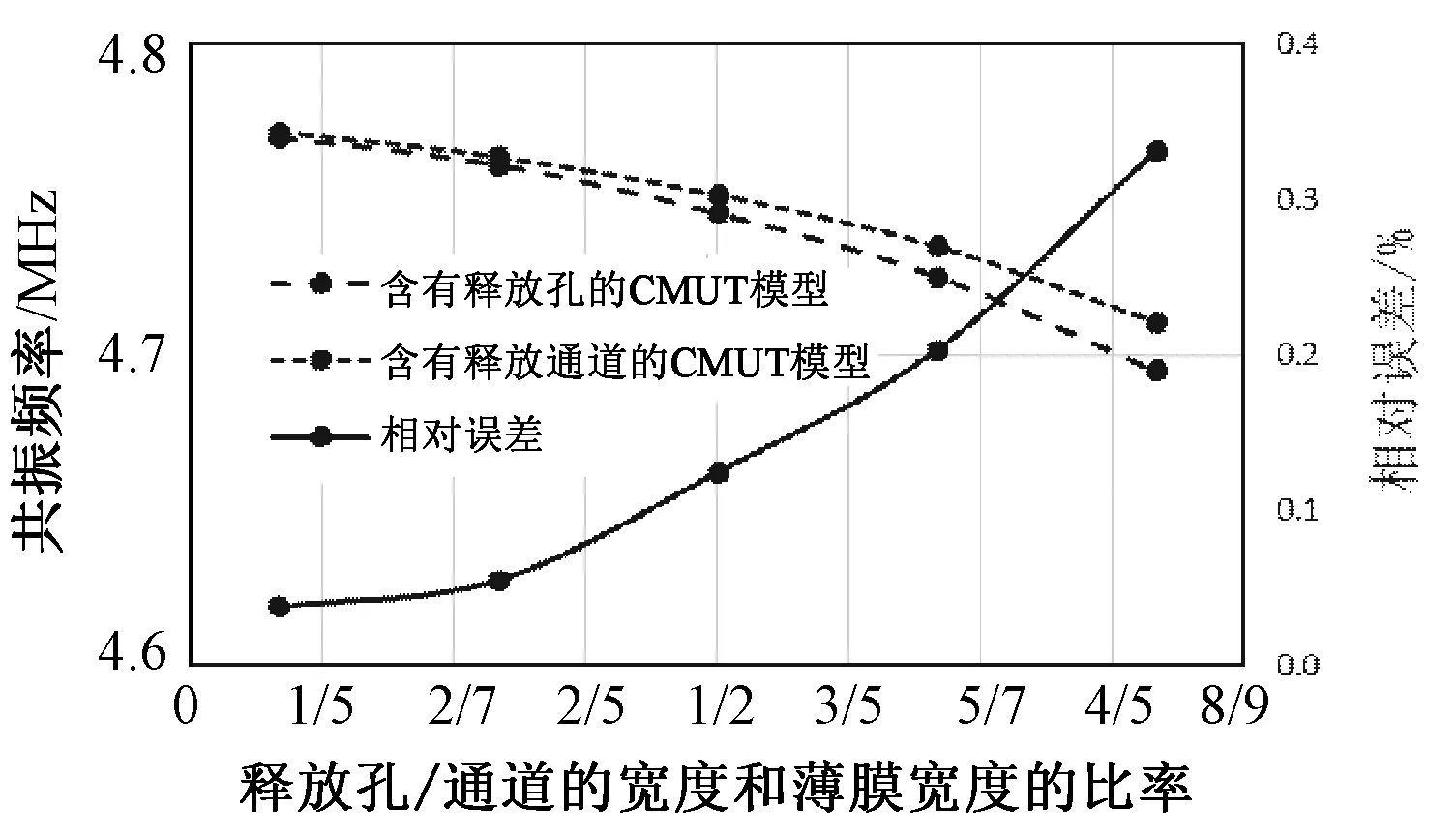
图15 释放孔参数对共振频率的影响及相对误差Fig.15 The relationship between parameters of etching hole vs. resonant Frequency

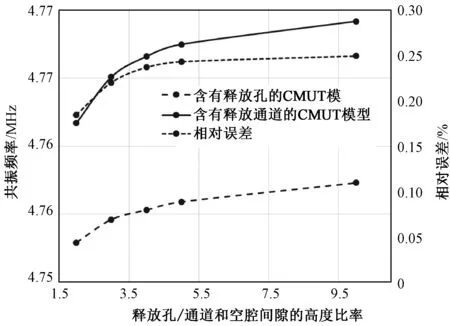
图16 释放通道参数对共振频率的影响及相对误差Fig.16 The relationship between parameters of etching channel vs resonant frequency

2.5 实验结果

图17为验证有限元模型的仿真结果搭建的实验平台和测试结果。由图17(c)可以看出，加工出的传感器结构的共振频率为2.41 MHz。

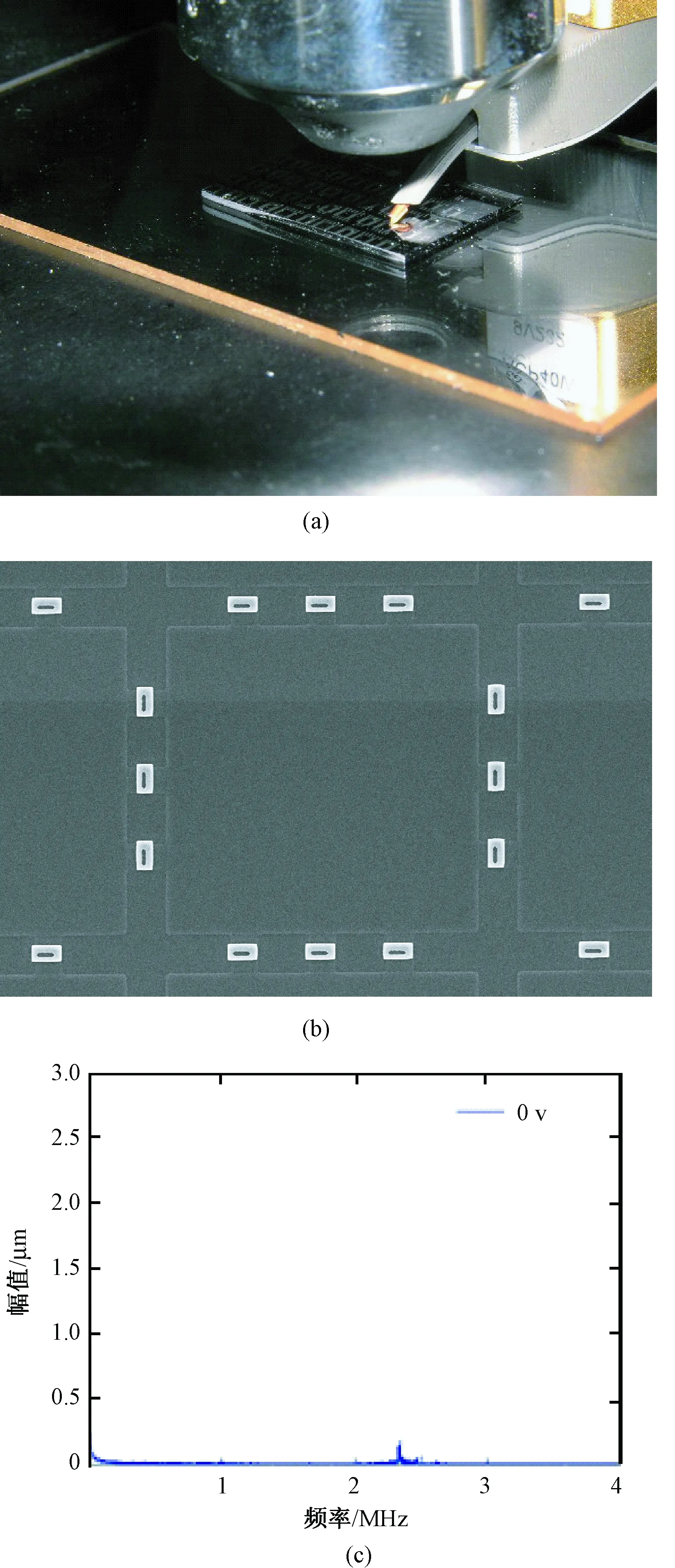
图17 共振频率的测试。(a)实验平台；(b)CMUT的俯视图；(c)共振频率的实验结果Fig.17 Measurement for resonant frequencies. (a) The experimental platform; (b) SEM of CMUT; (c) The result of test for resoant frequencies

3 讨论

建模通常是CMUT设计的第一步。通过构建合适的模型，对影响CMUT特性的结构参数进行分析仿真，寻找影响CMUT特性的参数功率，为其设计和应用打下坚实的基础。对于CMUT的建模，根据牺牲层释放法的特点分别建立了4种模型，并对这4种模型进行了仿真。

首先构建了一种最简单的矩形振动薄膜CMUT模型，对影响其共振频率变化的两个最主要的参数(长宽比和厚度)进行了仿真。从仿真结果来看(见图6、7)，薄膜厚度增加，CMUT的共振频率增加；随着长宽比的增加，系统的共振频率显著下降，当长宽比增加到2时，下降趋势趋于平缓，大于4时，共振频率的变化很小，趋于不变。振动薄膜的厚度增加，CMUT结构的刚度会增大，故而系统的共振频率也增大。矩形薄膜CMUT模型是最简单的模型，可以用于初估传感器的特性参数—共振频率。为了能更精确地分析CMUT的特性，我们又根据牺牲层释放法构建了另外3种CMUT模型，分别是CMUT的BOX模型、含有释放孔的CMUT模型和含有释放通道的CMUT模型。并对4种CMUT模型分别进行了仿真，并进行对比。

将矩形薄膜CMUT模型和CMUT的BOX模型的仿真结果进行了对比分析，由图8、9可知，两者变化趋势基本一致，但是差异还是比较明显的。随着长宽比的增加，百分比差异从7.25%增长到8.7%；当厚度从0.5 μm增加到2.0 μm过程中，最小的百分比误差值也在7.5%左右。

采用牺牲层释放法的CMUT支撑墙需要有释放孔，第3种含有释放孔的CMUT模型就是模拟这种结构，更接近于实际CMUT结构。从3种结构的仿真结果对比分析来看(图10、11)，矩形薄膜CMUT模型与BOX模型和含有释放孔的CMUT模型的结果相差较大，尤其在长宽比较小的情况下，甚至高达20%。随着长宽比的增加，仿真结果的差异在长宽比达到4时，差异变化趋于稳定，在10%附近。无论是矩形薄膜CMUT模型与含有释放孔的CMUT模型相比，还是CMUT的BOX模型与含有释放孔的CMUT模型相比，仿真结果的差异在长宽比较小的情况下，仿真结果的差异较大，当长宽比达到和大于4时，CMUT特性趋于一致，差异不大。

通过对图12、13的仿真结果的分析，可以看出，4种CMUT模型无论是在长宽比较小，还是较大时，仿真结果的变化趋势都是一致的。不同之处在于矩形薄膜CMUT模型的仿真结果与后3种的CMUT模型差异较大，而后3种的CMUT模型在长宽比小于3是有一些差异；当长宽比大于4时，仿真结果趋于一致。图13中，矩形薄膜CMUT模型与含有释放通道的CMUT模型的比较曲线可知，仿真结果的相对误差在薄膜长宽比较小时，差异比较大；随着长宽比增加，相对误差逐渐变小，长宽比大于4时，相对误差稳定在8.7%。

含有释放通道的CMUT模型最接近实际的CMUT结构。从图14可以得出结论，后3种模型随厚度增加，共振频率的变化趋势基本一致，并且都与矩形薄膜CMUT的差异较大。含有释放通道的CMUT模型最接近实际的传感器结构。如图16所示，当释放通道的高度逐渐减小时，结构的共振频率逐渐增加；在空腔的高度与释放通道(或者释放孔)的高度大于4时，共振频率基本不再发生变化。

第1种矩形薄膜CMUT模型是最简单的模型，只考虑矩形薄膜，薄膜四周的约束采用固定约束。这种模型是以前研究的用牺牲层释放法加工的电容式微机械超声传感器采用的模型，分析简单且容易。但是，实际加工后的形状如图1所示。矩形薄膜的四边是由侧墙支撑，当振动薄膜受力变形后，支撑薄膜的四边侧墙由于是弹性体，也会发生随着薄膜的变形而变形，并不像第1种模型中固定支撑那样不变形。所以，第2种BOX模型与第一种模型相比，考虑了支撑墙的影响，共振频率会因结构的刚度减小而减小，如图10所示。实际上，在采用牺牲层释放法加工电容式微机械超声传感器时，需要有释放孔和释放通道，第3种和第4种模型就是考虑牺牲层释放法的工艺特点而构造的模型。第3种含有释放孔的BOX模型仅考虑在支撑墙上的释放孔，支撑墙的刚度进一步削弱。第4种含有释放通道的BOX模型考虑了释放通道的影响，因为释放通道实际上是加强了结构的刚度，但影响不大。此模型最接近实际结构，更符合实际情况。而第1种矩形薄膜模型没有考虑侧墙的刚度及释放孔和释放通道的影响，是不易用作采用牺牲层工艺制造的CMUT传感器。

为了验证本研究所建模型的有效性，对采用牺牲层技术加工得出的电容式微机械超声传感器进行了初步测试，图17(c)为测试结果。当电容式微超声传感器的振动薄膜边长为80 mm、厚度为1 mm时，采用含有释放通道模型仿真的共振频率为2.5 MHz，与实验结果图17对比(薄膜的初始电压为0 V)，误差为3.9%。从而可以验证本研究所建模型的有效性。

4 结论

本研究在分析牺牲层释放工艺对CMUT结构影响的基础上，提出了4种CMUT模型，即矩形。分别对4种模型进行了计算机仿真，分析了结构参数如振动薄膜的厚度和薄膜长宽比对CMUT性能的影响，并对4种模型的仿真结果进行了对比分析。结果显示，采用牺牲层技术加工的CMUT，与通常分析采用的振动薄膜模型的仿真结果的相对误差较大，对采用牺牲层技术制造的CMUT建立模型时，应考虑CMUT中支撑振动薄膜的侧墙及牺牲层的释放孔和释放通道的影响，即需考虑加工方法对结构的影响。