面向复杂网格模型的快速分层算法研究

（中科院广州电子技术有限公司，广州 510070）

0 引言

熔融沉积制造（Fused Deposition Modeling，FDM）技术是目前应用最为广泛的三维打印技术之一，在注塑模具、医疗、玩具、汽车、电子以及个人定制等领域得到大量应用[1,2]。FDM的制造原理是分层累积成形，其制造过程中每一层都是通过数据处理软件将数字化三维模型切片后得到截面轮廓，然后规划生成打印设备喷头的运动轨迹并输出到打印设备进行成形制造。分层切片算法是3D打印软件的关键内容之一，不仅是实现离散堆积成形的重要环节，而且对成形速度、成形精度、零件表面质量等方面都有很大影响。

针对三维打印模型的分层切片算法研究包括两个主要方面，其一是基于CAD（Computer Aided Design）几何模型的直接分层切片[3,4]，其二是针对离散化网格模型的分层切片方法。CAD模型具有完整的曲面数学表示，可以通过求解数学方程获得分层轮廓的数学表达式，因而其截面轮廓更精确，数据量也更小，但这种方法的不足之处是数据交换导致应用的困难，这是因为CAD模型的边界表示模型不同厂商之间具有相对差异性，难以在三维打印软件中统一处理，制约了基于CAD模型分层处理软件的实际应用。解决这一缺点的一个主要方法将各种CAD数据格式转化为标准化的数据格式，其中最为典型的是针对STEP（STandard for the Exchange of Product Model Data）标准几何模型的分层切片算法[5,6]，但仍存在转换过程中的容差差异等系列问题。目前3D打印软件系统大都采用离散化面片模型作为其数据输入格式[7]，这类模型数据格式公开而简洁，是事实上的三维打印软件数据输入格式标准，被主流商业软件系统所采用，如美国3D Systems公司的Dimension，比利时Materilise公司的MagicRP等。由于网格模型的离散化表示，需要大量求交运算以得到分层切片，因此提高其计算效率对于算法非常重要[8]，这方面的一个重要思路是建立三角网格之间拓扑关系以降低计算量，如基于信息继承对三角网格进行分类和排序等方法[9,10]，这类方法需要对数据结构进行良好的优化以降低内存消耗。网格模型分层的一个不足之处是层级台阶现象导致加工表面的粗糙，解决这一问题的一个有效方法是进行适应性的分层[11,12]，即基于模型表面的粗糙程度或者精度要求，适应性的变化分层厚度，而不是用单一的厚度来进行分层切片。

3D打印技术是制造史上的巨大突破，其市场前景远大，但竞争也日趋激烈，要在激烈的市场竞争中占有一席之地，三维打印设备必须从各方面提高其性能。面向三维打印的数据预处理技术对于提高三维打印质量非常关键，在性能近似的硬件设备中，更好的数据预处理能够使类似的硬件设备产生更好的打印效果，从而提高打印设备的市场竞争力。高端的商业三维打印数据处理系统价格昂贵，而开源系统在商业应用上的许可制度等因素，大大影响了我国三维打印行业的进一步发展，开发具有自主产权的三维打印软件系统，对于缩小我国三维打印与先进国家的差距具有重要意义。

针对目前三维打印设备数据处理软件现状，我们研发了具有自主知识产权的数据预处理软件系统，提出了网格模型分层切片技术，针对面片数较多并且形状复杂的大模型进行了效率性能方面的改进优化。接下来对该方法进行阐述，其中第一部分为算法总体框架，第二部分为算法的具体实现细节以及关键点介绍，第三部分介绍了轮廓区域界定方法，第四部分给出了系统实现和实例讨论，最后给出论文总结。

1 基于拓扑跟踪的网格分层切片算法概述

网格分层切片算法是按照三维打印设备的层高要求，从最低端到最高端依次获取模型的截面轮廓，为后续驱动FDM设备喷头的运动路径规划做准备。当模型变得复杂并且网格数目较多时，分层效率和稳定性尤为关键。为此，我们提出基于网格模型拓扑关系的快速分层算法，该算法建立了面向分层切片的网格模型半边结构，基于该结构依次求取相邻面片的交线，并自动形成首尾闭合的轮廓线，然后基于轮廓层次结构树生成轮廓加工区域，总体框架如图1所示。该算法以三角网格模型为输入，以分层切片区域为输出，其关键在于如何高效的建立模型的拓扑关系，并尽量降低内存耗费，其次是如何快速跟踪求交，得到轮廓的各个线段，最后是如何判断轮廓的包含关系，得到模型的轮廓截面区域。

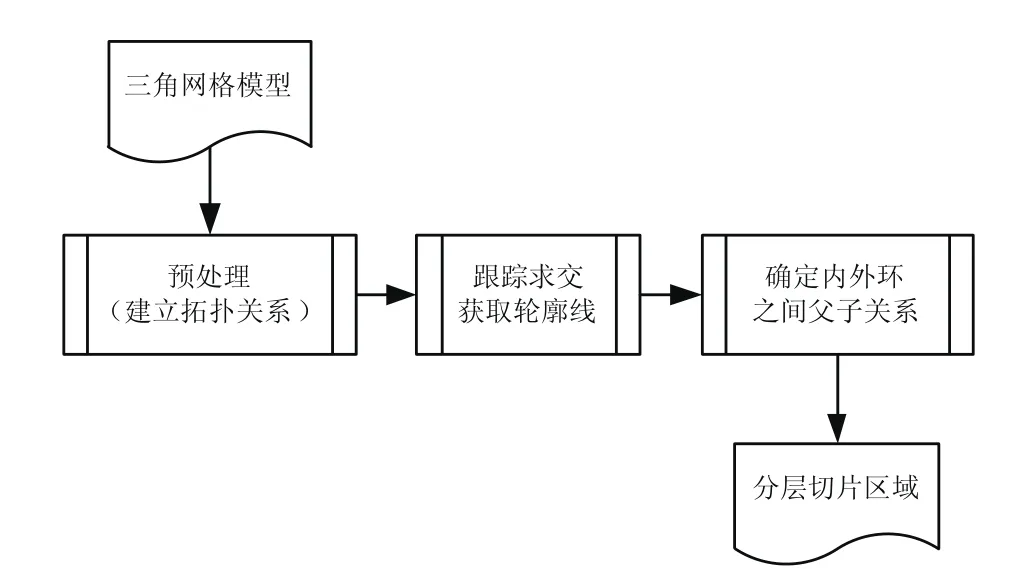
图1 分层切片算法框架

2 基于拓扑跟踪的轮廓快速获取

2.1 网格模型半边数据结构建立

基于半边结构建立网格模型的拓扑结构，并面向三维打印快速分层需求，在该结构中加入相应的数据结构以提高求解效率，如图2所示。其特点是每条边分裂为两条半边，其表示极为简洁，并可以非常容易地实现邻边查找、边遍历、点所关联边查找等关键操作。为实现轮廓线快速求取，我们将该半边结构进行扩充，增加了每条边的斜率以及当前的截面法向及是否为水平方向等信息。由于三角网格模型只是记录了三角形的顶点信息，因此需要在建立该结构时，判断三角形的公共边，这可以基于顶点建立红黑树排序来降低顶点比较次数，提高计算效率。

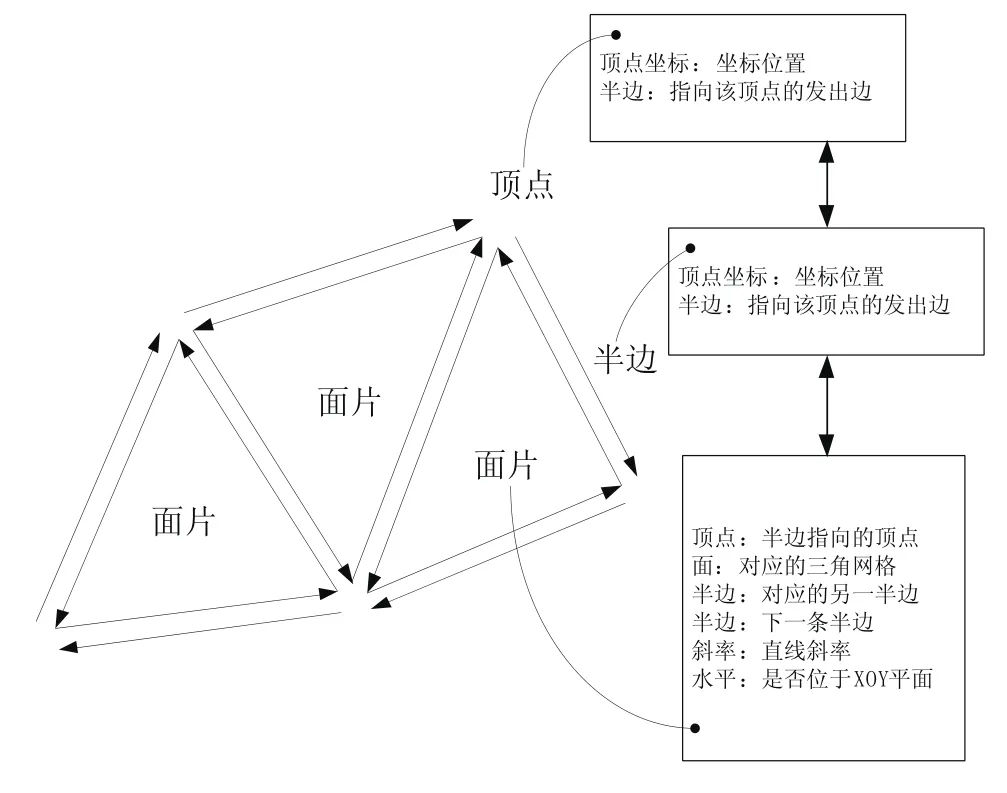
图2 面向分层切片的三角网格半边结构表示

2.2 轮廓线追踪求交算法流程

基于建立的网格模型拓扑结构，我们给出了图3所示的分层轮廓线求解算法。该算法的核心是基于一个初始相交三角网格，通过拓扑关系依次追踪求解至终止边界。

图3 基于拓扑追踪的分层切片算法

该算法可以实施的一个前提是网格模型的每个面片具有特定的法向，如图4所示，即每个三角形的边走向是一定的，其法向指向模型物体的外部。图4中，B所表示的Z平面中，假设初次获得的相交三角形是F1，则容易求得交点P1、P2，则线段方向为P1P2。基于P2所对应的半边，容易得到下一个三角网格为F2，顺次求解，可以得到一个完整的轮廓线。图4中给出了存在的奇异情况A，即交点为三角形顶点，这种情况下，只需要遍历围绕该顶点所有三角网格，直至遇到具有两个不同交点的面片即可，如图中的F3。

图4 追踪求解图示

三角网格与切面的交点求解只需要求解与每条边的交点。图5为分层平面与三角网格的交点情况，分别具有1、2、3个交点，即分别与1、2、3条边相交，在算法中只需记录两个交点以及每个交点对应的半边。

图5 平面与三角网格交点情况

不同的交点情况影响到求解轮廓线的过程。如图6所示，其初始三角形为F1。对于情况B，其求解交点过程是按照F1的走向依次对边进行求解，显然轮廓追踪终止边界为F2，即依次追踪求解到F2即可得到当前的完整轮廓线。但对于A情况，由于其交点为锥形端点，因此追踪边界为F4，为实现上的方便，我们取F2、F3、F4的集合作为追踪终止边界。

图6 追踪终止边界情况

3 分层切面区域定义

已经求得的边界轮廓线需要定义其走向以确定分层切面的内部区域，以进一步确定打印喷头所需要填充的区域。如图7所示，其中蓝色区域为模型的内部区域，而数字1到8所标识的轮廓线即为前述算法所确定的轮廓边界线。

图7 分层轮廓区域定义示意图

确定有效加工区域算法基本思路是：将所有的轮廓线两两判断相互包含关系，将被包含的轮廓线定义为包含轮廓线的子轮廓，同时将其层级加一，若相互无包含关系，则勿需操作。上述计算结果是定义了每个轮廓线的所有子轮廓线，同时计算了子轮廓线与其先辈轮廓线的层级距离，最终结果实际形成了轮廓线之间的父子关系树，显然，层级差为1的轮廓线之间组成了一个片连续加工区域，从而确定了分层切片的内外轮廓。基于上述算法，图7中的轮廓线层级关系树如图8所示。

图8 轮廓线层级关系树（针对图7）

4 系统实现与实例分析

在Windows平台下，采用C++在Visual Studio 2013开发环境下实现了三维打印数据处理软件系统，该系统采用本文所介绍算法对STL模型进行分层切片。以下基于模型实例验证分析本文算法的有效性。

图9为采用该算法处理的一个复杂框架模型，该模型顶点数为40482，三角网格面片数为81752，物体长、宽、高分别为55、55、55。图10为高度为1.375时，分层截面的形状，图11为高度为23.375时的分层切片。图12为对模型逐层切片后的结果，生成该切片数据大约需要3秒时间，其中的层高为0.25。

图13为需要打印的一个工艺品模型，该模型顶点数为59818，三角网格数为：124316，物体长、宽、高分别为90、95、43。图14为高度为4.125时分层截面的形状，图15、16分别为高度为10.375、24.625时的分层截面形状。图17为对模型逐层切片后的结果，生成该切片数据大约需要4秒时间，其中的层高为0.25。

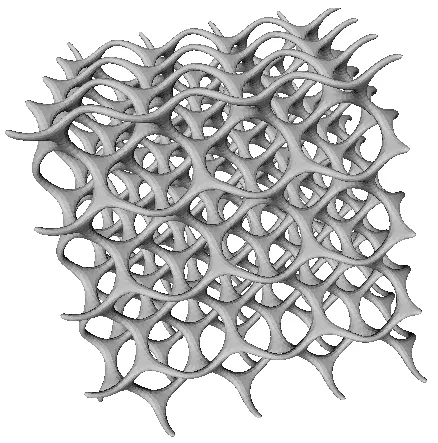
图9 框架网格模型

图10 高度1.375截面轮廓

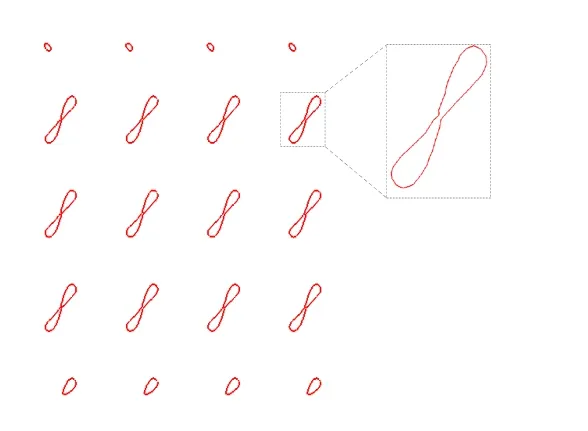
图11 高度23.375截面轮廓

图12 模型总体分层轮廓（模型图9）

图13 工艺品网格模型图

图14 高度4.125截面轮廓

图15 高度10.375截面轮廓

图16 高度24.625截面轮廓

图17 模型总体分层轮廓（模型图13）

5 结论

给出了一种基于网格模型拓扑关系追踪求交的三维打印分层切片算法，通过对网格模型基于半边结构建立面向分层切片的内在拓扑关系，在求解时可以基于半边关系追踪求交并得到轮廓线，勿需基于交点重新组合轮廓线，不仅降低了运行时间，而且可以降低由于容差带来可能的轮廓错误，并基于轮廓层级关系树确定有效加工区域。该算法数据结构简洁，计算效率高，内存耗费低。实例表明该算法稳定可靠，特别是针对复杂网格模型具有良好的效率和鲁棒性。