基于回归分析的磨料水射流加工深度预测研究

黄涛涛，何雪明，陈泽华，张 荣，纪小刚

（1.江苏省食品先进制造装备技术重点试验室，无锡 214122；2.江南大学 机械工程学院，无锡 214122；3.江南大学 理学院，无锡 214122）

0 引言

磨料水射流（Abrasive Water Jet，AWJ）加工技术[1]作为一种新兴的冷态加工技术，与传统加工方法相比，具有加工材料广泛、加工稳定性好、加工质量高、加工柔性高、无刀具磨损以及绿色环保等独特的优越性，在航空航天、电子、船舶、汽车、机械等领域具有十分广阔的应用前景。

目前国内外越来越多的专家学者开始注重研究磨料水射流加工技术。国内，张福炀等[2]将高压水射流切割技术应用于硝基胍发射药制备切药过程，通过建立磨料水射流切割材料的力学模型，对切割过程的安全性进行了研究。王军等[3]对玻璃纤维增强塑料的水射流切割工艺进行了试验研究，分析了主要加工参数对切割效率、切割断面粗糙度、切缝宽度的影响关系。彭家强等[4]对磨料水射流铣削对金属材料的去除力和去除模型进行了研究，为金属的铣削加工和切削去除分析提供了理论借鉴。冯衍霞等[5]对磨料水射流铣削氧化铝陶瓷的铣削表面形状进行了试验研究，并分析了铣削工艺参数对铣削表面形状的影响。国外Ushasta Aich等[6]分别对不同的金属、石材等进行了磨料水射流切割加工，分析了磨料水射流切割原理。Messelink等[7]利用磨料水射流对球面工件进行了精铣光整加工，证明了磨料水射流用于精加工的可行性。Massimiliano Barletta等[8]通过实验研究了磨料水射流的流速、磨粒粒径与工件的表面加工质量和材料去除效果的关系。但是国内外对磨料水射流铣削加工深度准确控制方面的研究相对较少。

本文在正交实验的基础上，结合回归分析方法，分析了AWJ加工45#材料时加工参数对加工深度的影响，建立了加工深度预测模型，为AWJ铣削加工合理地选择铣削加工工艺参数，精确控制铣削深度奠定了基础。

1 AWJ铣削加工原理

磨料水射流铣削加工，即通过调整加工参数，使得射流不射穿工件，在工件表面去除一定量的材料，从而达到表面精铣及成形铣削加工的目的。如图1所示，磨料水射流以一定角度冲蚀工件时，磨料对于工件表面的作用力FW可以分解为水平剪切分力Ft与竖直冲击分力Fn，即使射流与工件表面垂直，射流中大部分磨粒仍与工件表面成一定角度。

磨料水射流加工参数决定了磨粒对工件表面作用力的大小，水平剪切分力Ft可以使磨粒对工件表面尖锐凸起进行刮擦磨削，从而使材料如同刨削一般被磨粒刮擦去除，而竖直冲击分力Fn对工件进行冲击挤压作用，可以在工件表面产生裂纹，并使材料发生脆性断裂去除。

图1 磨料水射流铣削加工微观示意图

2 AWJ铣削加工深度预测模型

2.1 试验系统及材料选择

本文采用DWJ3020-BB-X5型数控磨料水射流加工机床进行AWJ加工深度试验，如图2所示。

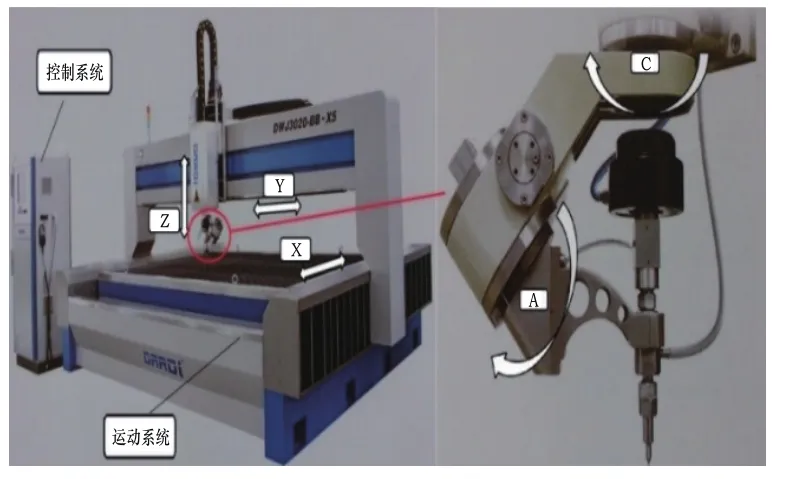
图2 DWJ3020-BB-X5数控水射流加工机床

入射角采用90°，即射流垂直于工件表面；磨料采用80目石榴石，工件材料采用45#。为减小误差影响，每条切缝在不同位置测量三次，取其平均值，如图3所示。

图3 磨料水射流加工深度试验

2.2 AWJ加工深度试验设计

以加工深度h为试验指标，对磨料水射流切削加工45#时的主要加工参数：喷嘴移动速度v、射流压力p和靶距S进行试验，采用三因素五水平正交试验设计，如表1所示。

本试验选取了三个影响因素，三个空白因素，每个因素取五个水平值，根据正交试验的特征，需要进行25次相关试验，记作L25(56)。如表2所示为详细的正交试验表。

表1 磨料水射流加工水平试验因素表

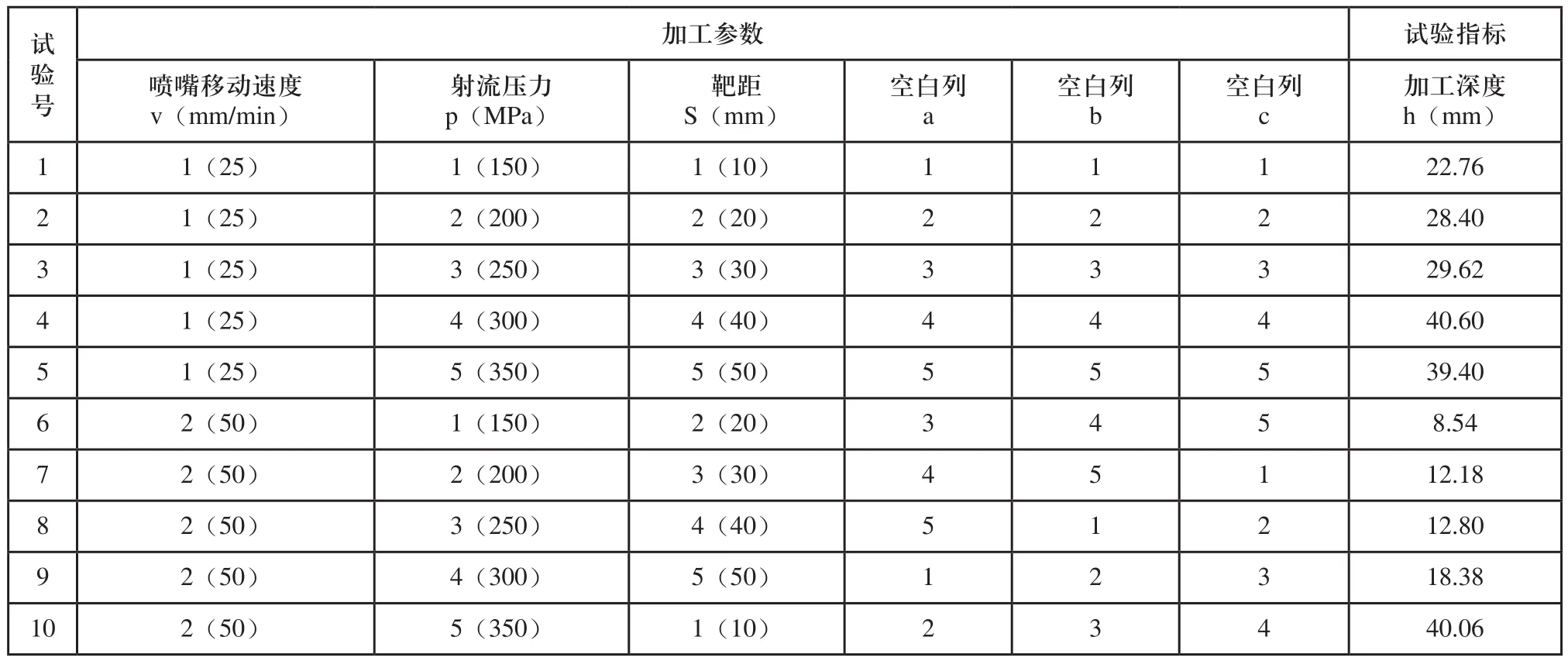
表2 磨料水射流加工正交试验表

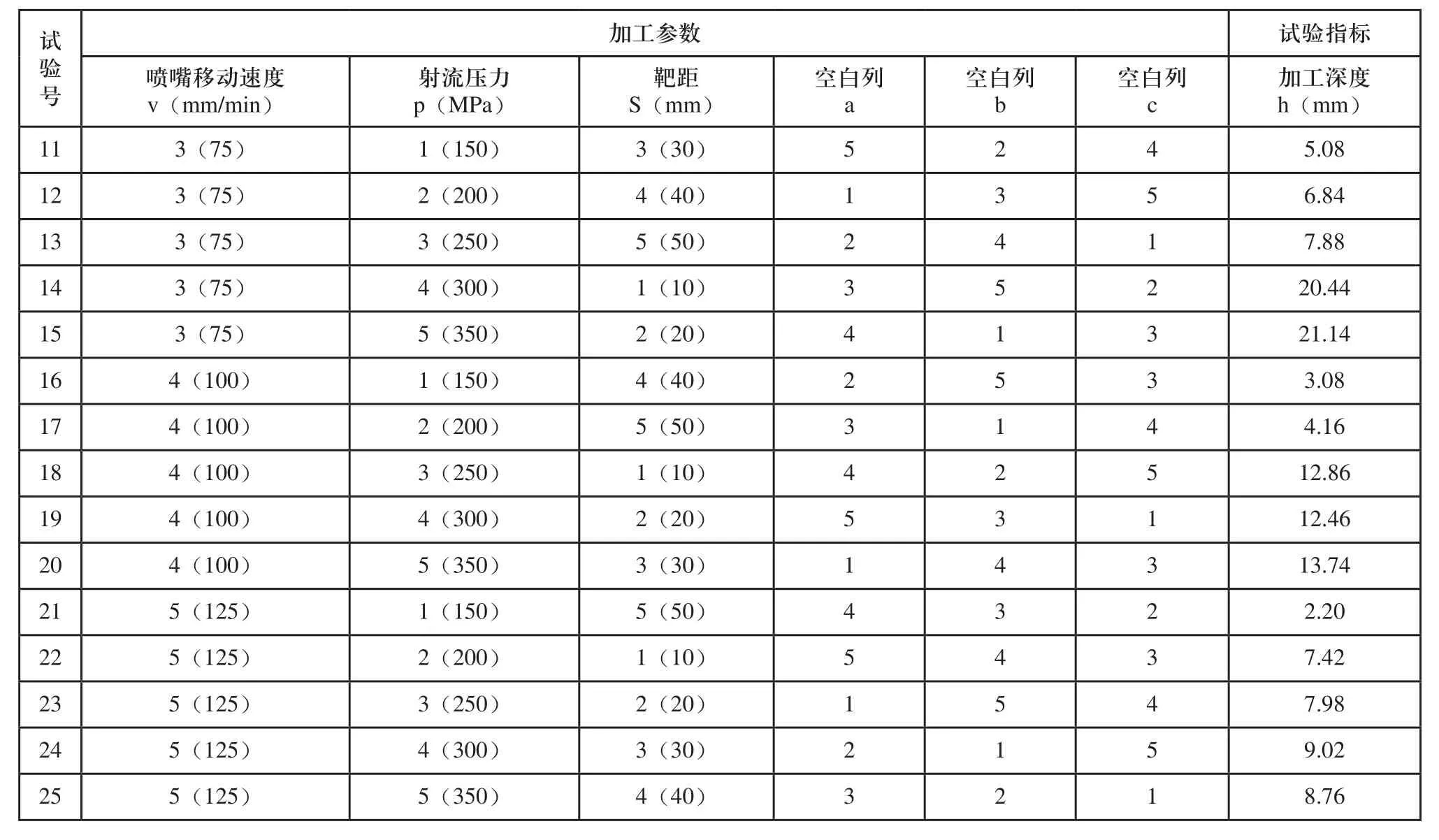
表2 （续）

一般通过极差分析和方差分析来处理正交试验数据，分析各影响因素对试验指标的影响显著性。极差分析相较于方差分析具有计算简单，直观等优点，所以这里采用极差分析方法。

极差分析公式如下:

其中，Ⅰj，Ⅱj，Ⅲj，Ⅳj，Ⅴj分别表示第j列因素“1”、“2”、“3”、“4”、“5”水平所对应的试验指标数值的平均值；极差Rj表示第j列因素水平变动对试验指标的影响力。Rj越大，影响就越大，反之就越小。

根据式(1)得极差分析表如表3所示。

表3 加工深度h（mm）极差分析表

根据表3所示的正交极差分析结果，Rv＞Rp＞RS，即对加工深度影响的三种因素主次顺序为喷嘴移动速度v、射流压力p、靶距S，且Rv、Rp、RS均大于空白因素的极差，证明了数据的可靠性。Ⅰv＞Ⅱv＞Ⅲv＞Ⅳv＞Ⅴv，说明随着喷嘴移动速度v的提高，加工深度h在减小；同样，Ⅰp＜Ⅱp＜Ⅲp＜Ⅳp＜Ⅴp，说明随着射流压力p的提高，加工深度h在增加，ⅠS＜ⅡS＜ⅢS＜ⅣS＜ⅤS，即随着靶距S的提升，加工深度g在减小。

2.3 AWJ铣削深度回归分析模型的建立

1）一般模型的建立

对加工深度h（mm）影响最大的加工参数有：喷嘴移动速度v（mm/min）、射流压力p（MPa）、靶距S（mm），一般模型采用幂函数：

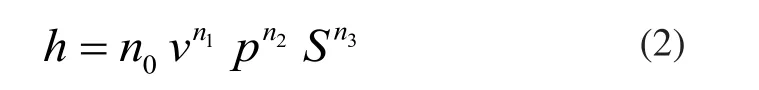
其中，n0、n1、n2、n3为待定系数。对式(2)两边同时取对数，得一次方程：

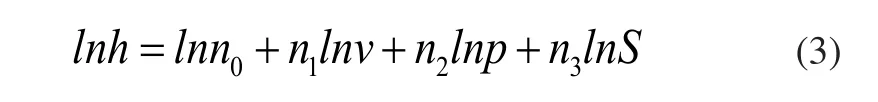
设：Y=lnh；B0=lnn0；Bl=nl；C=lnv；D=lnp；E=lnS

其中，l=1，2，3。

则：

由式(4)可得多元线性回归方程组：

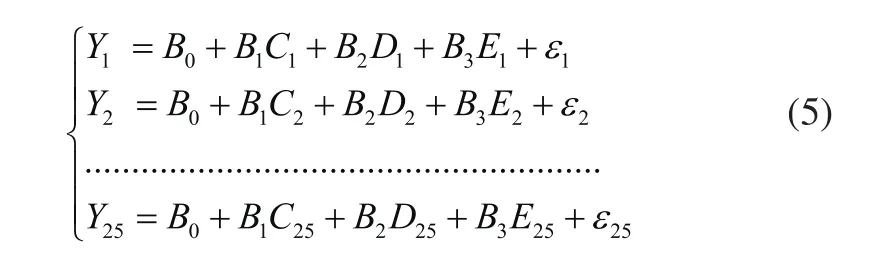
可得

设b0、b1、b2、b3分别为B0、B1、B2、B3的最小二乘估计量，根据最小二乘法估计，可以得出经验回归方程为：

2）回归方程

基于正交试验的25组样本数据，应用MATLAB软件进行回归分析，命令为：[b,bint,r,rint,stats]=regress(Y,X,alpha) ，其所得回归方程为一次方程，即方程(3)，所以在样本数据输入时要将试验样本数据做取对数处理。

其中：b为常数项与回归系数；

bint为回归系数的区间估计；

r为残差；

rint为置信区间；

stats为检验回归模型统计量，有四个数值：相关系数r2，F值，f值，概率P；

alpha为方程显著性水平。

运算后得回归方程为：

stats表示用于检验回归模型的统计量，r2= 0.9938，F=1129.8367，f=2.3203e-23，P=0.0044。r2越接近1，F＞f值，F越大，则表面回归方程越显著；与F对应的概率P＜alpha时回归模型成立，alpha一般取值0.05。

上述结果说明，回归方程每个变量的选取都是有效的，且该回归预测模型成立。

将回归方程(9)回归幂函数形式，如下：

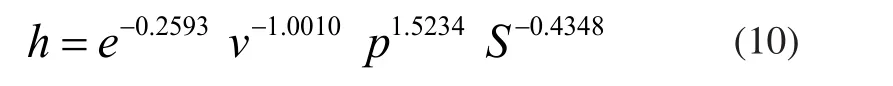
其中e为自然对数的底数。式(10)即基于正交试验的的回归预测模型。

在MATLAB软件下得残差分析图，如图4所示。

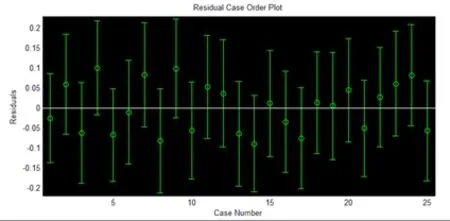
图4 残差分析图

残差分析图可以反应回归预测模型是否很好的拟合原始数据，如果残差均匀分布于零点两侧，且零点均在所有残差的置信区间内，则说明预测模型很好的拟合了原始数据，所得预测模型成立，若零点不在残差的置信区间内，则视为异常点，异常点对回归模型的精度有较大影响。图3中，所有残差均在0点附近均匀分布，区间几乎都位于[-0.2，0.2]之间，没有发现异常点。

综上所述，以上回归结果较为准确，对加工深度h（mm）的预测具有一定的指导意义。为了验证上面所得模型的准确性，下面将对参数范围内的其他参数下所得加工深度与实际加工数据进行对比，验证预测模型是否具有可靠性及可推广性。

3 实验验证

取表4中10组加工参数，进行实验验证，将实测值与预测模型的预测值进行对比分析。

表4 磨料水射流加工预测模型验证试验参数

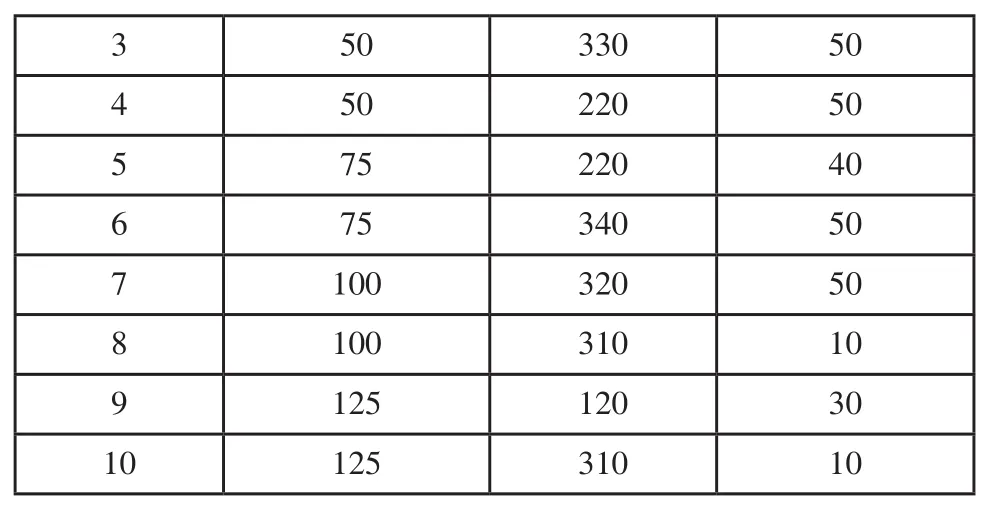
表3 （续）

将表4中10组加工参数用上述基于正交试验的回归预测模型进行预测，所得结果如表5所示。

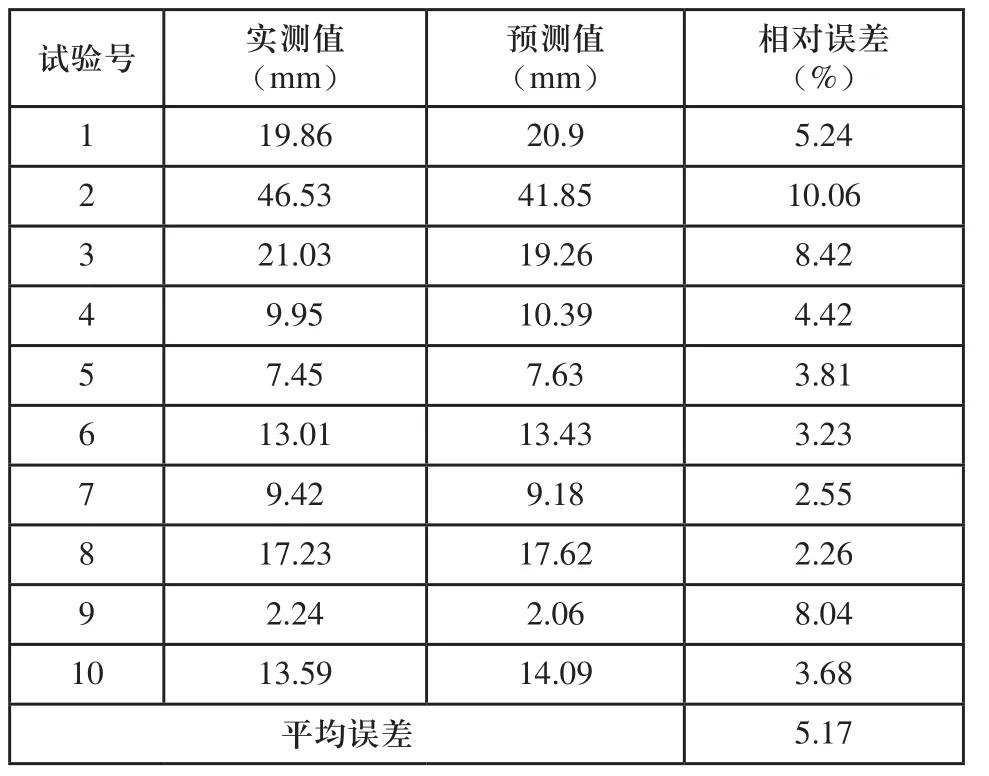
表5 预测结果及相对误差

从表5中可以看出，基于正交试验的回归预测模型最大相对误差为10.06%，最小相对误差为2.26%，平均误差为5.17%，具有很高的可靠性。

4 结论

1）在正交试验的基础上，运用极差分析方法分析了喷嘴移动速度v、射流压力p、靶距S三个参数对磨料水射流加工45#材料加工深度的影响，得到加工深度影响的三种因素主次顺序为喷嘴移动速度v、射流压力p、靶距S。

2）运用回归分析方法，建立了以加工深度为核心的预测模型，并通过实验进行了验证，得出基于正交试验的回归分析预测模型平均预测相对误差为5.17%，具有很高的可靠性。