基于高斯过程机器学习算法的高校课堂教学质量评价模型

2019-01-18傅翠霞罗亦泳

东华理工大学学报(社会科学版) 2018年4期

傅翠霞，罗亦泳,2

(1. 东华理工大学外国语学院，江西南昌 330013；2. 武汉大学测绘学院，武汉 430079)

教学是大学的立校之本，而课堂教学又是教学最重要最核心最本质的部分，是人才培养的主阵地。对课堂教学质量进行合理的评价是提高教学质量和教学管理水平的有力保障。要实现对课堂教学效果的准确评价，必须建立可靠的教学质量评价模型。但是，由于教学包含教与学的动态过程，影响教学质量的因素众多，影响因素对教学质量影响程度不一，并且评价指标与教学效果之间存在复杂非线性关系，以致难以构建准确、可靠的教学质量评价数学模型。因此，教学质量评价数学模型构建研究成为当前热点研究问题[1，2]。

教学质量评价建立即构建教学质量评价指标与教学效果之间的函数关系。当前，课堂教学质量评价方法较多，高校通常采用绝对评估法、评等法、相对评估法、评语法和综合评分法等方法。这些方法操作起来简单，但方法过于主观，这些方法的评价结果与教学质量真实状况之间存在较大差异。近年来，模糊聚类分析法、灰色关联法、神经网络算法、支持向量机等智能算法在教学质量评价中得到一定的应用，并取得一定的效果[3-8]。但这些算法的稳定性有待于提高，并且不能分析结果的可靠性。因此，如何构建一种受人为主观影响小、结果可靠性高、模型参数自适应的教学质量评价新模型成为当前研究趋势及难点。高斯过程(Gaussian Process，GP)是近几年基于高斯随机过程与贝叶斯学习理论提出的一种新的机器学习方法[9]。高斯过程是一种具有概率意义的核学习机，算法可同时获得计算结果及结果不确定性数据。因此，算法在分类、拟合、模式识别等复杂问题中得到较好应用，在教学质量评价研究中未见相关研究。鉴于GP算法优点及教学质量评价问题的特点，将其运用于实现对高校教师课堂教学质量进行更加全面、合理和有效的评价，对促进教师的教学水平和学校的教学质量的不断提高具有积极的意义。

1 教学质量评价的GP模型构建

GP模型构建过程中，首先利用训练数据集，并根据贝叶斯原理，求取超参数的最大后验似然估计值[10]。然后，依据GP模型，建立训练样本条件概率的负对数似然函数。再对超参数求偏导，并采用共轭梯度优化方法，自适应确定GP模型的最优超参数解，最终得到基于最优超参数构建高斯回归模型。

构建教学质量评价模型过程中，利用GP算法对训练数据集进行学习，以确定GP模型的超参数。基于超参数建立教学质量评价模型，可实现教学质量评价估计，并估计评价结果的方差。具体步骤如下。

(1) 建立训练数据集。设训练数据集{xi,ti}，i=1Λm，其中xi=(xi1,xi2,Λ,xid)为第i个样本的d个教学质量评价指标值，作为GP模型输入，ti为对应教学质量评价结果，作为GP模型输出，m为训练数据集样本数。

(2) 建模数据归一化。为消除数据由于量纲的影响，对训练数据集行归一化，归一化公式如(1)所示。

(1)

(3)GP模型超参数自适应计算。对学习样本进行学习，通过学习样本的对数似然极大化自适应获得GP的最优超参数θ。

(4)教学质量评价模型建立。基于GP的最优超参数θ，估计输入X*的教学质量结果Y*。

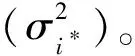
(2)

2 基于GP的教学质量评价模型实例

为验证教学质量评价GP方法的有效性，收集了2个不同的教学质量评价实例。分别基于GP模型建立教学质量评价方法，并建立对应置信区间。

2.1 基于实例1的教学质量评价GP模型(本科课程)

采用张吉刚、梁娜等人确定的7个教学质量评价指标，参考文献[11]收集到24个教学质量评价样本。以前16个样本作为GP的训练数据集，后8个样本作为测试数据集。基于训练数据集建立GP模型。利用GP模型对训练数据集、测试集的教学质量评价结果进行计算，并计算对应的方差及置信区间，具体计算结果如表1所示。

表1 例1的教学质量评价的GP方法结果

由表1可知，GP模型能很好地表达实例1中的教学质量评价指标与评价结果之间的复杂关系。GP模型估算的训练数据集、测试集的方差较小，并且教学质量评价结果理论值均落在置信区间内，证实教学质量评价的GP方法结果可靠。

2.2 基于实例2的教学质量评价GP模型(高职课程)

参考文献[12]确定12个教学质量评价指标，以浙江商业职业技术学院某课程学生测评的数据为例，对20个样本进行随机排序，并以前15个样本作为GP的训练数据集，后5个样本作为测试数据。GP模型具体计算结果如表2所示。

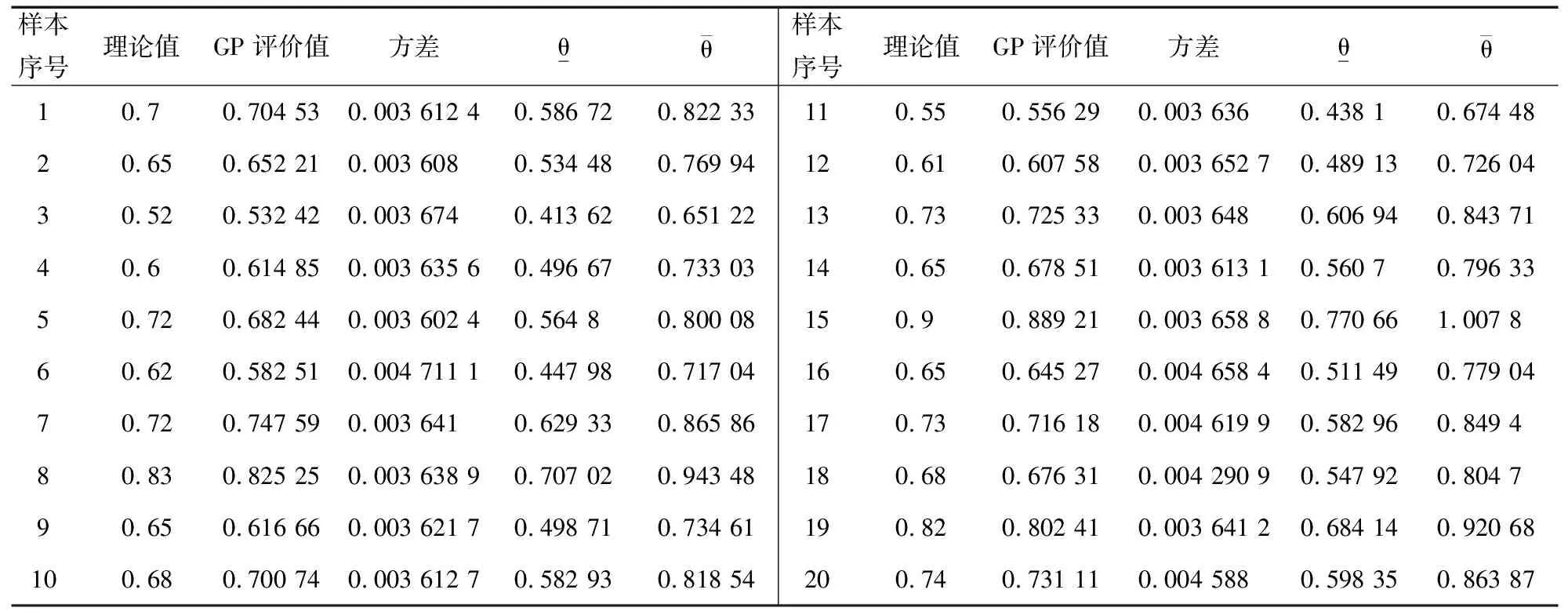
表2 例2的教学质量评价的GP方法结果

由表2可知，对于实例2中采用12个教学质量评价指标，基于GP算法的教学质量评价结果的方差较小，并且评价结果理论值均在对应置信区间内，证实GP方法对于不同教学质量评价问题具有较好的可靠性。

2.3 模型对比分析

为验证GP模型的精度的优劣，利用BP神经网络、最小二乘支持向量机(LS-SVM)算法建立教学质量评价方法，并进行精度对比。GP参数由模型本身自适应计算得到，BP神经网络结构与参数确定参考文献[13]，LS-SVM利用遗传算法优化得到[14]，具体各模型核心参数见表3、4所示。利用3种模型计算实例1、实例2的测试数据集的教学质量评价结果，并选取平均绝对误差(MeanAbsoluteError,MAE)、平均相对误差(MeanRelativeError,MRE)、均方根误差(RootMeanSquareError，RMSE)等3个精度指标评价各模型精度优劣，对教学质量评价新方法的精度做出科学的评价，指标计算公式参见文献[14]，具体各模型的精度结果如表3、4所示。