浅滩影响下的近岸低频波浪研究

李绍武，李博文，柳 叶，廖智凌

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

海洋中的波能主要集中在周期为3～25 s的波浪中，这部分波浪称为重力波；周期在25～300 s范围内的波浪能量也占了一部分，这部分波浪称为次重力波，即低频波浪。Munk[1]在海岸地区首次发现这种低频(也叫长波)运动。大多数的港口结构物和港口布局对周期3～25 s的短波有良好的掩护效果[2]，然而对周期在25～300 s之间长波的掩护十分困难，而这部分波浪对海岸附近泥沙输运[3-5]、港内水面波动[6-7]和系泊船的稳定等都有不同程度的影响。低频波在珊瑚礁地形的产生和传播规律已有很多研究。有研究表明，入射波浪通过珊瑚礁时，波能耗散主要集中在礁前缘的几个波长长度内，而长波能量会在入射波通过礁顶时增加[8]。McComb et al.[9]也发现Geraldton港的近岸地区，低频波波能主要来自涌浪经过近岸地区宽3 km礁坪时转化的能量。长波在潜堤地形的研究也有丰富的成果，如，于博等[10]实验研究了波浪在潜堤上的变形规律和长波在潜堤上的生成机制，并探究了水流对长波特性的影响。陈杰等[11]对不规则波在潜堤上的传播变形以及与潜堤的相互作用进行了研究。

相比珊瑚礁地形和潜堤的影响，浅滩地形范围更大，坡度更缓，地形更为复杂多变，由此产生的低频波可能对港内泊稳条件产生隐患。低频波在浅滩地形上的传播研究成果也较少。本文以海口港马村港区海域设施建设工程为例，应用非静压波浪模型SWASH模拟近海区域浅滩地形影响下波浪变形，并进行长短波分离后，再对低频波的演变规律进行研究。

1 计算模型及其控制方程

SWASH(Simulating Waves till SHore)是由代尔夫特理工大学开发的非静压波流数值模型。该模型基于包含非静压项的非线性浅水方程，能够有效地模拟非线性相互作用、波流相互作用、破碎、爬坡在内的波浪变形。计算表明，SWASH模型垂向取两层即可获得与Boussinesq方程相当的色散精度，取三层时色散精度远好于Boussinesq方程。

非静压模型SWASH的控制方程是不可压缩流体雷诺时均N-S方程。在笛卡尔坐标系下，控制方程的垂向二维形式为

(1)

(2)

(3)

式中：t为时间；u(x、t)、w(x、t)分别为x、z方向的流速；ρ为密度。另外，静水压力ph=ρg(ξ-z)，g为重力加速度，ξ为水面高度，pnh是非静压项。紊动压力ταβ由k-ε模型紊流黏性近似得到。

2 模型验证

先用实验资料对SWASH模型进行验证。

2.1 双色波验证

表1 水槽试验中的双色波条件Tab.1 Condition of bichromatic wave in flume test

图1 水槽地形及测点布置Fig.1 Topography and stations of flume

参照Van Dongeren et al.[12]的双色波实验，建立二维水槽模型(图1)。因本文关注点在于地形和长波，选取A1和A4两组极端情况进行模拟，其中A1组底坡最缓，A4底坡最陡。不同组次波况如表1。SWASH数值模型采用时间步长△t=0.001 s，网格尺寸△x=0.01 m，垂向分为两层，曼宁系数取0.01。在频域内进行长短波分离，将模拟结果的水位时间序列用快速傅里叶变换的方法生成一个有限傅里叶序列，将时域过程转化到频域。然后将所有关注频域以外的傅里叶振幅设置为0，保留关注频域内的傅里叶振幅，进行傅里叶逆变换，将频域转化回时域，得到一列只有长波的水位时间序列，并统计其波高。模拟的波高结果如图2，可以看出模拟的向岸短波波高的沿程变化、破波点位置及破波区内的能量耗散趋势均与实测值较符合。长波均方根波高在A1组和A4组之间有明显的差别。A1组长波均方根波高沿程增加，在25 m前有微小振荡；而A4组均方根波高也在沿程增加，模拟区域产生显著振荡。A4组显著振荡的存在是由于反射长波的存在形成驻波。总体看来，A1组和A4组短波均方根波高和长波均方根波高的模拟与实测值吻合，因此可以认为SWASH模型对于双色波在相对较缓坡度的斜坡产生的长波模拟效果较好。

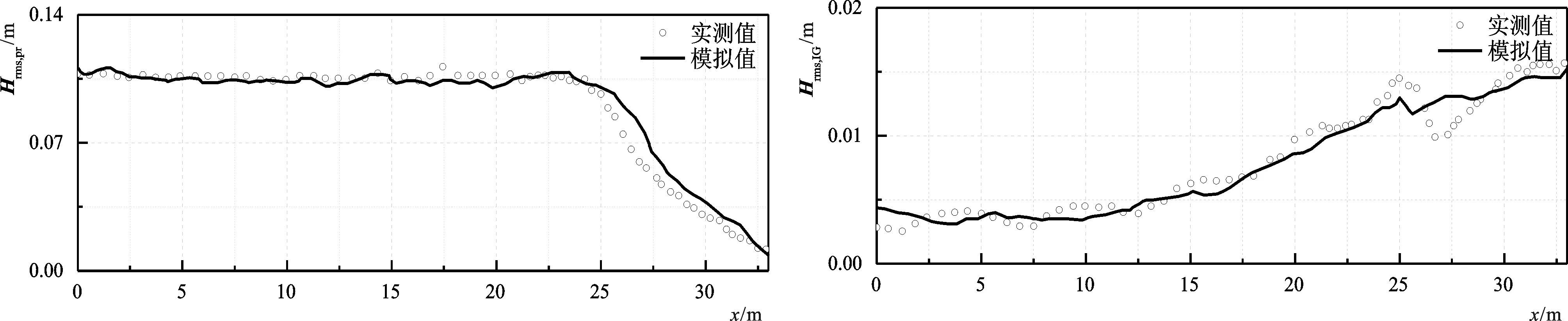
2-a A1组短波均方根波高模拟值与实测值对比 2-b A1组长波均方根波高模拟值与实测值对比

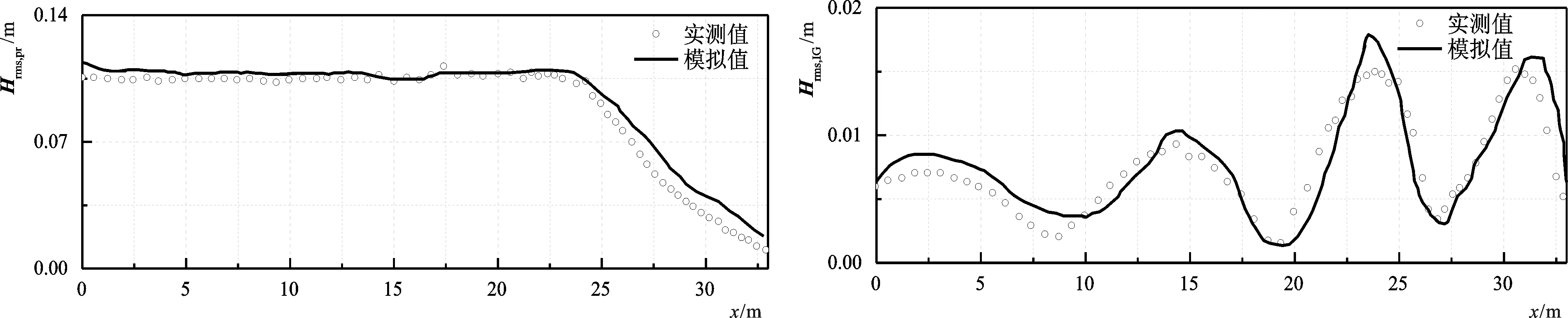
2-c A4组短波均方根波高模拟值与实测值对比 2-d A4组长波均方根波高模拟值与实测值对比图2 模拟值与实测值对比Fig.2 Comparison between simulated and experimental data

组次Hm0(m)Tp(s)A0.1572.05B0.2622.03C0.1033.33

2.2 不规则波验证

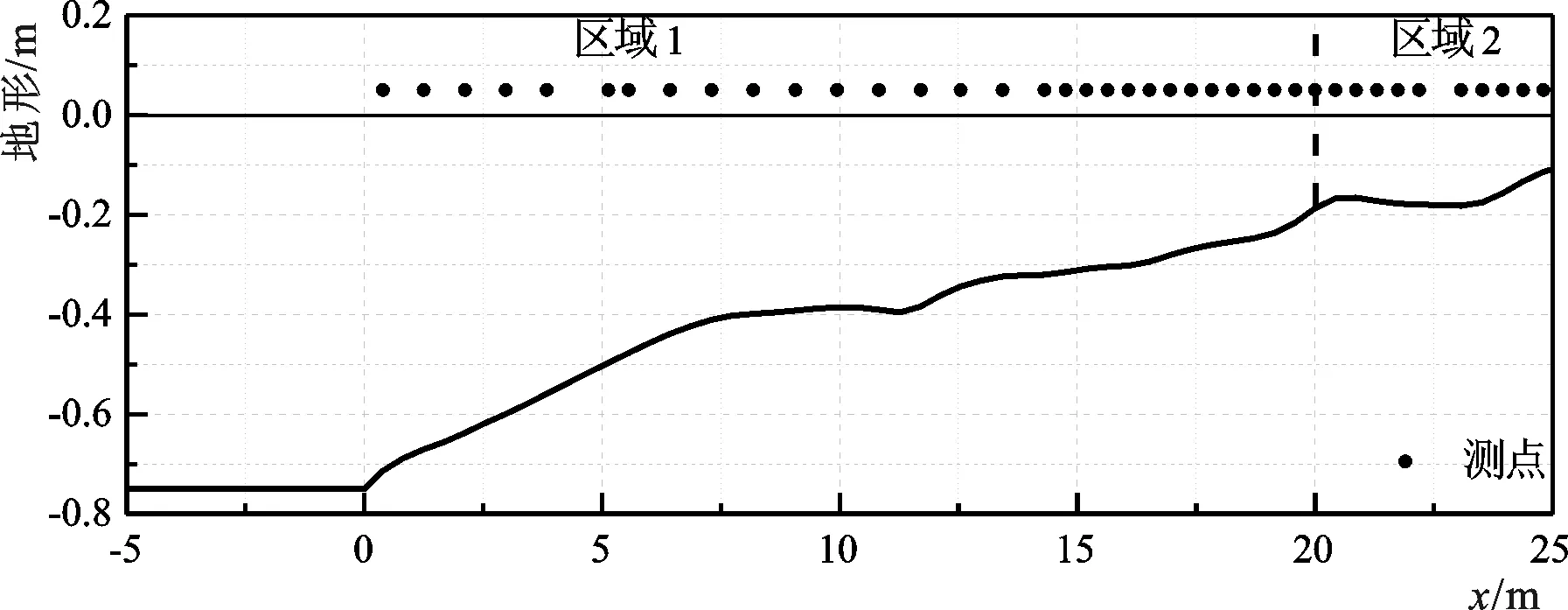
图3 试验水槽布置及测点位置Fig.3 Topography and stations of flume

参照Boers[13]的不规则波在近岸沙坝上的传播实验，建立二维水槽模型(图3)，不同组次波况如表2所示。模型网格尺寸△x=0.02 m，时间步长设置为△t=0.000 25 s，曼宁系数为0.03。为满足计算精度垂向分为两层。在3个组次中，C组试验的破波点在近岸的沙坝处，是坡度最缓的情况，能够最有效地模拟出长波的产生和传播，因此选择C组进行验证，波高为Hm0=0.103 m，周期Tp=3.33 s。试验区域分为两个部分，区域1为短波的浅水变形区域，区域2为破波区域。对比了短波有效波高Hm0,ss和长波有效波高Hm0,IG(图4和图5)。从图4看出，短波有效波高的模拟值和实测值基本一致。从图5看出，在区域1中，长波有效波高模拟值低于实测值，并且模拟值的斜率略大于实测值的斜率；在区域2，模拟值也与实测值有微小偏差。在区域1长波有效波高模拟值略低于实测值，分析应该是模型对于自由长波的反射模拟较差，或者在区域2耗散较大，导致反射回区域1的自由长波能量较少，而水槽实验中长波反射较模型大，使区域1波高模拟值小于实测值。总体看，SWASH模型可用于沙坝地形下长波的模拟。

图4 短波有效波高模拟值与实测值对比Fig.4 Comparison of the significant wave height between simulated and experimental data of short wave图5 长波有效波高模拟值与实测值对比Fig.5 Comparison of the significant wave height between simulated and experimental data of infragravity wave

3 长波的工程案例分析

3.1 工程概况及模型设置

选取的工程实例为海口港马村港区工程。海口港马村港区位于琼州海峡南岸，海南岛北侧澄迈湾水域，马村港区西起澄迈湾的玉苞角，东至东水村，地理位置和现有平面规划图见图6和图7[14]。港区位于向南凹入的岬湾中，岸侧为沙坝泻湖地貌，潮汐通道口门狭窄，湾口外侧存在浅滩，水沙条件较为复杂。根据水文资料，取入射波群方向为N向，波高为2.9 m，周期为6 s。

图6 海口港马村港区地理位置Fig.6 Geographical location of Macun area in Haikou harbor图7 海口港马村港区平面布置图Fig.7 Layout plan of Macun area in Haikou harbor

图8 试验地形及测点位置Fig.8 Topography and stations

组次滩顶水深(m)有效波高(m)谱峰周期(s)A132.96A232.98A332.910A432.912B132.56B232.76B332.96B433.16B533.36C112.96C232.96C352.96C462.96C572.96C682.96

因主要研究对象为浅滩地形，将波浪平面传播问题简化为纵剖面问题，忽略折射影响，提取浅滩典型剖面(剖面位置如图7直线所示位置)，为排除航道地形的干扰，将实际地形中航道处的地形进行光滑处理。数值水槽长4 656 m(图8)。造波区长300 m，为平底，通过坡度为1:100的缓坡与天然浅滩衔接。浅滩后为接近平底的缓坡，延伸到岸边。造波处水深为12 m。沿水槽方向计算网格步长为△x=4 m。时间步长△t=0.025 s，满足Courant准则。模拟时间1 h，数据采集时长为1 200 s。垂向计算网格均匀分为2层。依据所取参数不同，设置试验组A、B、C三组，分别研究不同入射波周期、波高和滩顶水深条件下长波的传播规律。在滩前、滩顶、滩后设置4个测点S1(距造波处724 m)、S2(距造波处884 m)、S3(滩顶位置，距造波处1 012 m)、S4(距造波处1 112 m)用以分析测点处频率密度谱。试验条件及测点位置设置如表3。从模拟结果中提取自由表面水位时间序列进行长短波分离，分别给出各组沿程各测点短波有效波高、长波有效波高、短波波能、长波波能以及能量密度谱结果。

3.2 波能演变

以A2为例研究浅滩上长波的能量增长规律。图9给出长短波波能沿程变化，其中E0为造波处波能。从图中可以看出，从坡脚开始，随着水深变浅，由于浅化变形，短波波能缓慢增加。短波波能增加到最高点时，大波发生破碎，波能变小。长波能量在造波区平底地形基本保持不变，随着水深变浅，长波能量快速增长，到达滩顶处，长波能量达到最大值，然后逐渐减小。

根据格林定律(Green′s Law)，自由长波波高随水深的变化与h-1/4成正比。Longuet-Higgins and Stewart[15]认为，在浅水条件下，约束长波波高的增长与h-5/2成正比。图10为SWASH模拟的浅滩上低频波的增长与Green′s Law(简称GL)、Longuet-Higgins and Stewart(简称LS)的理论增长的对比，以880 m处长波有效波高作为起始波高。从图10可以看出，长波有效波高的模拟值大致在LS和GL的理论值之间，总体上更接近LS理论值的趋势。这说明在浅滩上长波的组成成分是自由长波和约束长波的混合，但约束长波占主体。浅滩上长波的增长率大致与h-5/2成正比。从Battjes et al.[16]的试验发现，约束长波的增长率大于Green′s Law时，约束长波从其他频域的要素中获得能量，即短波能量向约束长波转化。

图9 无量纲化波能模拟值Fig.9 Simulated wave energy图10 浅滩位置长波有效波高和理论值对比Fig.10 Comparison of significant wave height between simulated and experimental data of infragravity wave on shoal

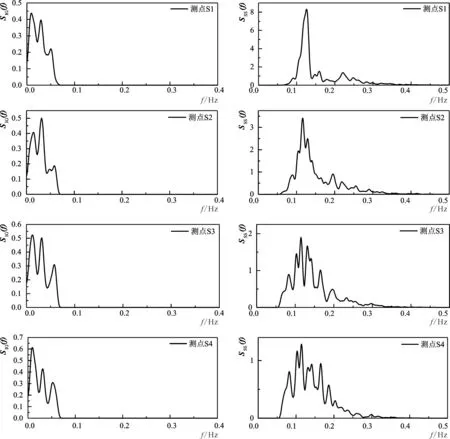
图11 S1～S4测点长波和短波的频率密度谱Fig.11 Power density spectrums of short wave and infragravity wave on stations S1-S4

为更清晰地看出沿程波能变化，图11给出测点S1～S4的低频波波能密度谱和短波波能密度谱，可以看出，从S1到S4测点，低频波波能持续增大，而短波波能持续减小，验证了上文提到的短波波能向低频波转化的说法。从长波频率密度谱中可以看出，长波的高频谐波逐渐增大，这种波能转化与长波的非线性相互作用有关。de Bakker[17]研究表明，4种形式的三波非线性相互作用造成波能转化，三波的组成可能包括一个、两个或三个长波成分。在缓坡上，长波的能量主要影响近岸水动力，而长波的相互作用主要导致长波波形变陡，最终导致长波破碎、能量耗散。研究表明，在风浪和涌浪破碎区外，短波能量大，长波能量转化回短波；而在浅水区，短波破碎，能量大部分已经消耗，主要是长波和长波之间的相互作用。van Dongeren et al.[12]发现长波之间的相互作用导致破碎，长波的耗散主要是由于长波与长波相互作用，导致高频谐波产生，长波波形变陡，最终导致破碎。在较平缓的地形上，这是主要的耗散原因。此处长波的耗散主要是由于长波之间的相互作用。

3.3 谱峰周期对长波演变的影响

图12和图13分别为A1～A4组次的短波无量纲化有效波高和长波无量纲化有效波高模拟结果，图中H0,ss为造波区短波有效波高,H0,IG为造波区长波有效波高,Hss为沿程短波有效波高，HIG为沿程长波有效波高。从图12看出，周期越长的短波波群有效波高越大，说明周期越长的短波波能降低越少，但整体呈减小趋势。在平底传播时，周期越长的波浪耗散越小。从坡脚开始，波浪开始爬坡，水深逐渐变浅，周期为8 s、10 s、12 s的入射短波有效波高增大，随着周期变大，有效波高增大越多，浅水变形效果越明显使得波能集中，波高增大。周期为6 s的入射短波波群在斜坡处波高减小。分析可能是波浪耗散影响大于浅水变形的波高增长。12 s周期的短波波群浅水变形效果最大,可以达到和深水波高比值为1。从图12看出，不同周期的短波破碎位置大致相同，下降速度大致相同。从长波有效波高图中看出，周期为8 s、10 s、12 s的短波波群产生的长波波高依次减小，短波周期越小长波的增长速率越高。在平底处长波波高基本不变，从坡脚后一段距离，长波波高增加，分析可能是因为平底水槽与斜坡距离较近，而长波振幅较小，传播到斜坡处时，破碎很少，几乎全部发生反射，反射的长波和入射的长波发生叠加，造成波高变大。到滩顶位置左右，长波波高达到最大，之后保持平缓，有轻微振荡。

图12 无量纲化的短波波高模拟值Fig.12 Nondimensionalized wave height for short wave图13 无量纲化的长波波高模拟值Fig.13 Nondimensionalized wave height for infragravity wave

图14 S1～S4测点长波和短波的能量密度谱Fig.14 Power density spectrums of short wave and infragravity wave on stations S1-S4

图14为测点S1～S4的能量密度谱，左边为长波能谱，右边为相应短波能谱。从长波能谱可以看出，A1组到A3组，长波能谱有较多的高频谐波，从测点S1到测点S4，波能向高频谐波转化。从总体来看，长波的能量均呈沿程增长趋势，周期越小的短波波群产生的长波能量增大越多；而短波的能量沿程逐渐减少。

3.4 入射波高对长波演变的影响

图15和图16为B1～B5模拟结果，图15为短波有效波高沿程变化，图16为长波有效波高沿程变化。从图中可以看出，短波相对波高越大，短波相对波高的减小值越大，有越多的短波能量减小；而对应长波波高的增长越小，能量并未全部传给长波。相对波高越小的短波生成长波的波高越大，波高的增长率也越大。长波和短波有效波高的沿程变化规律基本一致，短波破碎位置基本相同。图17从测点的能量密度谱来分析沿程长波和短波的变化情况。可以看出，相对波高较大的短波波群产生的长波能量更大，且向高频谐波转化更多。

图15 无量纲化的短波波高模拟值Fig.15 Nondimensionalized wave height for short wave图16 无量纲化的长波波高模拟值Fig.16 Nondimensionalized wave height for infragravity wave

图17 S1～S4测点长波和短波的频率密度谱Fig.17 Power density spectrums of short wave and infragravity wave on stations S1-S4

3.5 水位对长波演变的影响

图18和图19是C1～C6组的无量纲化短波有效波高和无量纲化长波有效波高变化图。从图中可以看出，短波由于底摩阻影响，有效波高沿程缓慢减小。滩顶水深1～5 m时，短波波高在滩顶发生骤降，说明由于水深变浅，短波发生破碎，波能迅速下降。滩顶水深大于6 m之后，短波波群有效波高平缓下降，说明由于水深增大，短波没有发生破碎。短波波群发生破碎的位置随水深不同而不同。明显可以看出滩顶水深为1 m，即水位最浅时短波先发生破碎。图19为长波有效波高的沿程变化图，从图中可以看出，整体上，滩顶水深1～5 m时，随滩顶水深增加，相同位置长波波高更大；但滩顶水深继续增大后，滩顶水深5～8 m时，随滩顶水深增加，相同位置长波波高更小。可以看出浅滩上短波波群产生的长波波高随滩顶水深增大而增大，到达峰值后，长波波高随滩顶水深增大而减小。长波波高增长最大时的浅滩水深约5 m。

图18 不同滩顶水深下无量纲化短波波高模拟值Fig.18 Nondimensionalized wave height for short wave with different depth图19 不同滩顶水深下无量纲化长波波高模拟值Fig.19 Nondimensionalized wave height for infragravity wave with different depth

图20为C1～C6组次测点S1～S4的能量密度谱，左侧为长波能谱，右侧为短波能谱。从图中可以看出，不同滩顶水深时，长波有效波高达到峰值的时间不同，在图20中，滩顶水深为1 m的C1组已经达到峰值，在S2、S3、S4测点依次减小，峰值约为0.25。从C2、C3、C4测点可以看出，在C1测点后，滩顶水深为5 m时短波波群产生的长波有效波高最大。从短波的能谱可以看出，S1～S4短波的能量在一直减小，而滩顶水深为8 m时产生短波波能最大，这是因为波浪发生破碎越少，能量耗散小。

4 结论

本文利用SWASH非静压波流模型，结合马村港区实际浅滩地形建立了二维垂向非静压数值波浪水槽，对跨越浅滩的长波特性进行了分析，主要结论如下：

(1)验证了SWASH模型对于长波的产生、传播模拟的准确性；

(2)浅滩影响下，长波主要由约束长波和自由长波组成，约束长波占主要部分；能量从短波波群向约束长波转化。长波增长率基本符合与h-5/2成正比的规律；长波波能来自于短波波群的能量转化。长波间的三波非线性相互作用，是长波耗散的原因。

(3)浅滩影响下，周期越短的短波波群产生长波波能更高。在工程实际中，应该对小周期的风浪采取更多的防范措施。相对波高越大的短波波群产生长波波能更高，但短波波群相对波高的变化对长波产生和传播趋势影响不大。相对波高较大的短波波群产生的长波能量更大，且向高频谐波转化更多。长波波高随着水位变化，变化趋势先随水位的增大而增大，到达峰值后随水位的增大而减小。谱峰周期为6 s，波高为2.9 m的短波，在滩顶水深为5 m时产生的长波能量最大，此工程上应特别关注水深为5 m的情况。

致谢：感谢国家超算天津中心为本项目计算提供的天河1号计算机资源。