沙溪口水电站坝下整治工程数学模型与物理模型比较研究

2019-01-18冯小香王义安

水道港口 2018年6期

张明, 彭伟,王斐,冯小香,王义安

(交通运输部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津 300456)

水工数学模型和物理模型是当前水运工程研究中普遍采用的技术手段，两者各有利弊。对于一些复杂的水运工程问题，数学模型和物理模型常相互配合[1-7]，以发挥各自的长处，并提高研究的精度。不过，目前数学模型和物理模型结果的相似性和差异性问题却缺乏足够研究，除在少数领域开展过对比研究外[8-10]，对于内河航道整治工程中的一些复杂问题进行对比研究的还较少，尤其是锁坝、明渠等对天然河道水流有明显影响的整治建筑物，因工程前后河道水流特性可能会发生比较大的变化，进行两者比较研究对于成果间的相互验证十分必要。

本文以沙溪口坝下航道整治工程为实例，通过比较分析，研究了数学模型、物理模型的锁坝分流量问题，对比了两者在航道水深、水位、流速等通航条件上的相似性和差异性，提出了滑梁水、剪刀水等碍航水流在数学模型中的识别方法。研究成果可为复杂水工模型试验提供参考，对同类航道整治工程也具有一定的借鉴意义。

1 模型试验方案

沙溪口水电站位于闽江干流沙溪与富屯溪汇合口下游约5.5 km，在水口水电站上游约108 km。沙溪口水电站坝下近坝段处于水口水库的回水变动区，当水口库水位较低时，该段河道比降大、水深浅、流速大，具有典型山区河流特性[11]。

沙溪口船闸下游设计最小通航流量为265 m3/s，天然情况下船闸下游水位仅63.07 m，比设计最低通航水位63.8 m低0.73 m，近坝段航道水深一般仅0.3～0.8 m(图1)，达不到航道设计水深2.1 m的要求。在航道升级整治工程中，拟采用锁坝、丁坝、明渠相结合的方案来抬高船闸下游水位，结合适当疏挖方式增加航道水深。鉴于整治方案的复杂性，研究采用数学模型进行了多组次方案的筛选试验，在此基础上，利用物理模型对方案效果进行了验证，并进一步对方案进行了优化。本文重点关注数学模型和物理模型试验成果的相似性和差异性问题，为便于对比，仅以设计方案为例进行说明，设计方案(图2)布置情况主要如下：

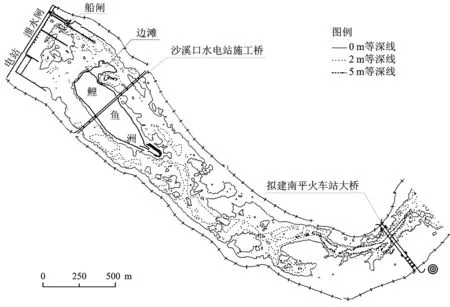
图1 沙溪口枢纽坝下河势图Fig.1 River graph of reaches downstream Shaxikou hydro-junction

(1)沙溪口坝下航道设计水深2.1 m，明渠上游段航道宽40 m，明渠内航道宽55 m，明渠下游段航道宽50 m。

(2)在右汊修建锁坝一条，坝长约184 m，坝顶高程63.8 m，坝顶宽2 m，迎水坡1 ∶2，背水坡1 ∶3。

(3)在左汊修建对口雍水坝，下接通航明渠一条，明渠长约1 660 m，顶宽100 m，渠首底高程61.1 m，渠尾底高程58.45 m，渠底底坡1.6‰，两侧渠壁高2.0 m，明渠右侧边坡1 ∶2.5，明渠左侧边坡1 ∶20。

(4)在左汊鲤鱼洲中部抛设一条丁坝SJ1，为防止流量大于265 m3/s时明渠右侧向明渠内产生滑梁水，在右侧明渠外的中、下部抛设两条丁坝SJ2和SJ3。

(5)对口壅水坝、明渠两侧挡墙坝顶宽1 m，对口壅水坝和明渠左侧挡墙的两侧边坡均为1 ∶0.5，明渠右侧挡墙的内侧边坡为1 ∶2.5，外侧边坡为1 ∶0.5。

(6)对左汊鲤鱼洲边滩进行局部疏挖，疏挖控制高程61.6～63.5 m；将明渠内航道的高点炸除，不足设计高程区域采用填筑块石混凝土填充，其它航段仅炸除高于设计底高程的浅点区域，近坝段航道的设计底标高见图3。

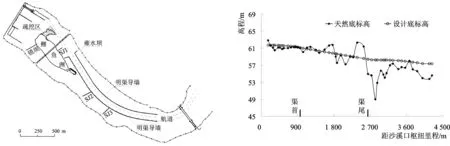
图2 设计方案平面布置图Fig.2 Layout of design scheme图3 坝下近坝河段航中线高程与设计底标高沿程变化图Fig.3 Natural and design riverbed elevations at mid-route along waterway downstream the dam

2 数学模型与物理模型简介

2.1 数学模型

2.1.1 控制方程

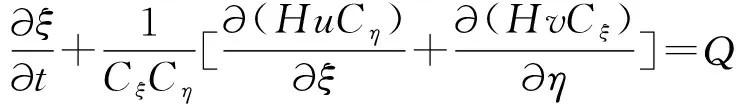
(1)

水平方向动量方程

(2)

(3)

式中：u、v，ω分别为ξ、η和σ方向的速度分量；t为时间变量；H为总水深；Q为单位面积的水量变化值；g为重力加速度；ρ0为水体密度；Pξ、Fξ和Mξ为ξ方向的静水压力梯度、紊动动量通量、动量的源(汇)，Pη、Fη和Mη为η方向的静水压力梯度、紊动动量通量、动量的源(汇)；Cξ和Cη为坐标转换系数；υV为垂向紊动系数。

2.1.2 计算网格

数学模型进口为沙溪口枢纽坝址，出口位于坝轴线下游约4.5 km。模型采用正交曲线网格，在计算域内共布置了735×270个网格，纵向网格平均尺度约6.1 m，横向网格平均尺度约2.5 m，明渠附近网格进行了加密处理，纵向网格尺度一般4～8 m，横向网格尺度一般1～4 m。

2.1.3 模型验证

模型计算地形为2015年实测地形。根据同年观测的270 m3/s、1 000 m3/s、1 800 m3/s三级流量下的水位、断面流速、汊道分流比对平面二维水流数学模型进行验证，验证结果表明，上述三级流量下，对于船闸最近的水位测站，模型计算的水位与实测水位相差仅-0.03 m、-0.07 m、-0.02 m，其它水位测站最大相差均在±0.1 m；模型计算断面流速分布与实测值基本一致，左汊分流比在上述三级流量下相差分别为-4.7%、-2.4%、-2.6%，数学模型验证的精度满足规范要求，可以用于航道整治工程的方案论证计算。

2.1.4 锁坝处理

锁坝会造成局部水头损失，数学模型将其能量损失在参量化后以源汇项的形式添加到动量方程中，主要以下式表示

(4)

式中：H0为锁坝顶部水深；△E为锁坝上下游的水头损失；△x为沿水流方向的网格宽度。

2.2物理模型

物理模型为1 ∶50的整体定床正态模型，按重力相似准则设计。模型范围自沙溪口水电站坝上1 km处至坝下4.5 km附近，模拟河段长约5.5 km，模型依据的地形与数学模型相同。

物理模型采用平面导线控制系统进行放样，采用断面法进行地形制作，平面误差和高程误差均控制在±5 mm以内。进口流量由西门子电磁流量计控制，测量精度为0.01 L/s(模型流量)，尾水位用带微调的翻板式尾门进行控制和调节，整体表层流场采用尚水公司研制的VDMS流场实时测量系统测量，测量精度为0.1 m/s(原型流速)，单个测点流速采用ACM2-RS型电磁流速计测量，测量精度为0.1 cm/s(原型流速)。

物理模型也采用三级流量对河道沿程水位、断面流速及左汊分流比进行验证，验证结果表明，在Q=270 m3/s、1 000 m3/s、1 800 m3/s时，对于船闸最近的水位测站，模型水位与实测水位偏差分别为-0.01 m、0.01 m、-0.08 m，其它测点的水位偏差一般在±0.10 m以内；各测流断面流速分布趋势、主流位置及流速大小与实测值基本一致；左汊分流比模型观测值与实测值偏差分别为-2%、-3.9%、-2.9%。

3 数模和物模试验结果比较分析

3.1 分流比

鲤鱼洲右汊修建锁坝后，其水流具有堰流特性，堰流水流形态与上游水位有关，水位流量关系可根据堰流的理论公式计算

(5)

(6)

式中：Q为流量；σs为淹没系数；ε为侧收缩系数；m为流量系数；g为重力加速度；Hw为堰顶全水头；H0为堰顶以上作用水头；a0为动能修正系数；υ0为断面平均流速。

将上式淹没系数σs、侧收缩系数ε取1，b取184 m时，在给定的堰顶以上作用水头H0后，查询流量系数，并根据迭代计算后可以得到锁坝理论最大过流量和水位流量关系，以此水位流量关系作为模型试验的参考约束值，与数学模型与物理模型得到的右汊过流量进行对比。

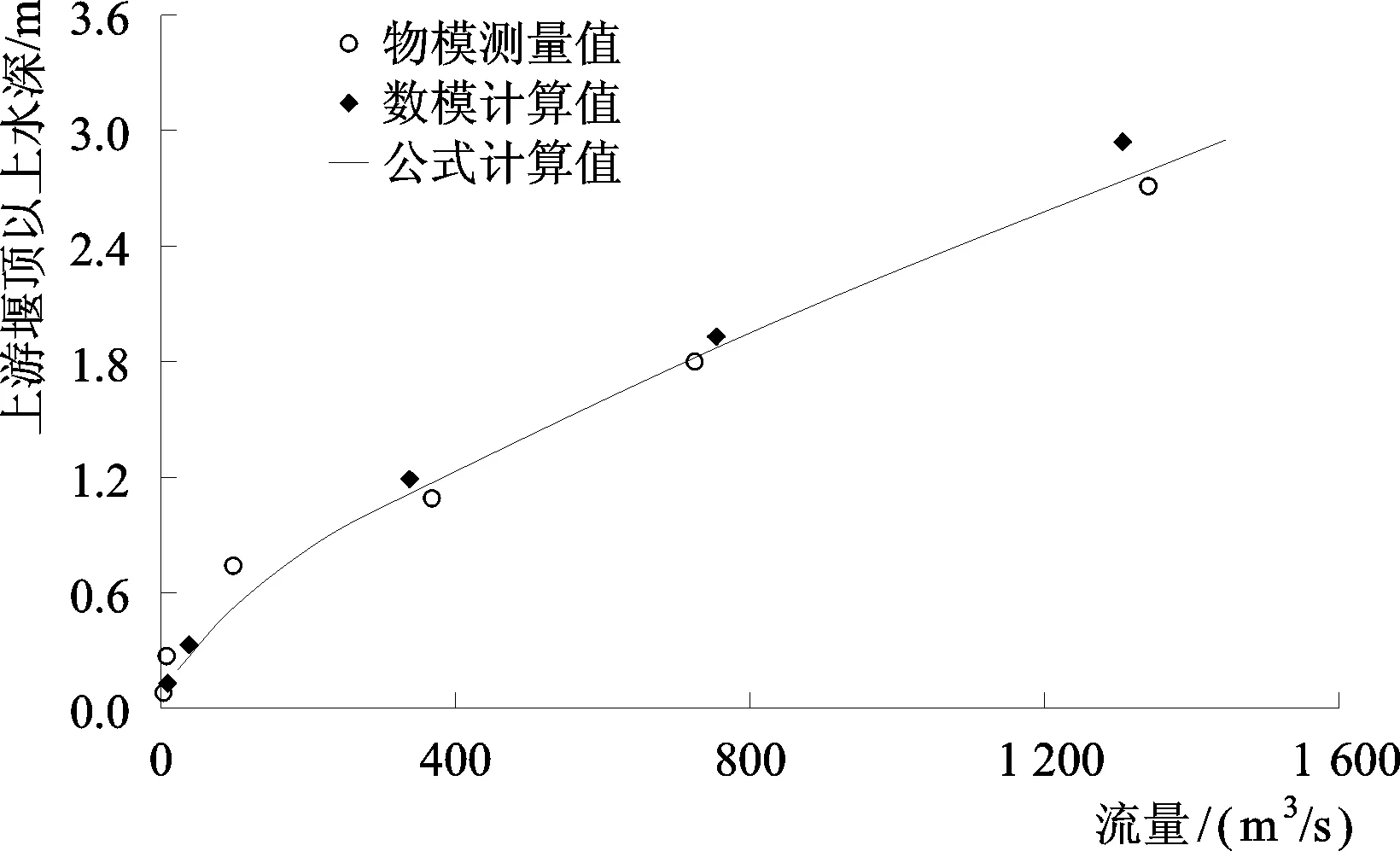
图4 锁坝上游水深流量关系Fig.4 Deep-discharge relationship of closure dike

由图4可见，在上游堰顶水深小于0.8 m时，相同水深情况下数学模型与物理模型的流量值均比理论计算值偏低，原因主要在于锁坝附近右岸岸边存在突嘴，小流量对锁坝过流存在一定的收缩效应；在上游堰顶水深为1～2 m时，如电站下泄流量Q=1 000 m3/s、1 800 m3/s条件下，相同水深情况下数学模型与物理模型的流量值比较接近，与理论公式计算值也相差不多；在上游堰顶以上水深约2.9 m时，如电站下泄流量Q=3 000 m3/s条件下，相同水深情况下，数学模型计算的右汊过流量比理论计算值偏大，可能是在洪水流量下，锁坝两侧边滩溢流，右汊实际过流宽度要大于锁坝长度，从而增加了数学模型计算的右汊过流量。

从数学模型和物理模型的左汊分流比来看，工程前后，数学模型和物理模型的结果总体上吻合较好，但个别流量级下仍存在一定的偏差。在对比的五级流量下，偏差较大的是电站泄流Q=353 m3/s时，数学模型与物理模型结果相差约9%，这主要是因为在相同流量下，物理模型水位偏低，导致其锁坝过流量偏少，同时因小流量情况下，分流量的少量变化对于分流比影响较大。在其余情况下，工程前后，各级流量下数学模型和物理模型的左汊分流比相差均在5%以内。

3.2 航道水位

因数学模型和物理模型建模时地形处理方式的不同，二者水位除一些控制性断面相差不多外，沿程其余测点处的水位并非都能吻合较好，往往存在一定的偏差。尤其是对一些缺乏验证资料的流量级，个别位置的水位测点，数学模型和物理模型结果有时还相差较大。此时若以绝对值进行比较，其结果因包含了两种研究方法的差异，而使得研究结果的差异进一步放大；而工程前后各自的水位相对变化值可以消除研究方法的差异，两者的变化规律一般较为一致。

从天然情况船闸下闸首水位来看，设计最小通航流量下(Q=265 m3/s)数学模型比物理模型高0.09 m，设计最大通航流量下(Q=3 000 m3/s)高0.3 m，但若从二者工程前后相对值的变化来看，最小通航流量、最大通航流量下数学模型水位分别抬升0.62 m、0.01 m，而物理模型水位分别抬升0.63 m、0.11 m，两者相差-0.01 m、-0.10 m。两者的规律基本一致，误差也更小。

3.3 航道水深

从数学模型结果来看，明渠出口向下游，由于下游航道开挖引起水位下降等原因，下游航道水深比设计水深2.1 m略有偏低，最小为1.79 m，位于明渠出口处。明渠中部由于水位雍高，航道水深在2.07～2.18 m，明渠渠首及沙溪口水电站施工桥桥区河段，航道水深在1.67～1.94 m间，鲤鱼洲洲头向上游，航道水深约为2 m。航道水深主要呈现两头低，中间高的特征。

物理模型航道水深的分布规律与数学模型计算值基本一致，但由于物理模型水位相对较低，航道水深也相应小些，明渠渠首上游约160 m处的丁坝SJ1附近，航道水深最小，仅为1.57 m。明渠内航道水深一般为1.62～1.8 m。

3.4 航道流速

采用实测垂线平均流速与表面流速之间的关系(图5)，将平面二维水流数学模型计算的垂线平均流速值转换为表面流速，并与VDMS采集的物理模型表面流速进行比较，以沙溪口水电站泄流Q=3000 m3/s时为例，从航道中心线流速来看(图6)，数学模型计算值与物理模型测量值的变化趋势基本一致，但局部位置仍存在一定的差异，如明渠尾部500 m航段，数模计算值整体上比物理模型测量值偏小，最大相差0.56 m，平均相差0.31 m，定义流速偏差率=(物理模型流速-数学模型流速)/数学模型流速×100%，其中流速偏差率取绝对值，则该段流速偏差率最大为24%，平均为13%。明渠进口500 m航段及明渠下游500m航段，流速偏差率平均分别为5%、6%。

对于沙溪口水电站施工桥桥区河段，在Q=265 m3/s、1 000 m3/s、1 800 m3/s、3 000 m3/s时，数学模型最大流速分别为2.45 m/s、2.72 m/s、3.04 m/s、2.92 m/s，物理模型最大流速分别为2.38 m/s、2.61 m/s、3.2 m/s、3.35 m/s，流速偏差率分别为2.9%、4.0%、5.3%、14.7%，上述典型流量级下，数学模型与物理模型结果总体上差别不大。

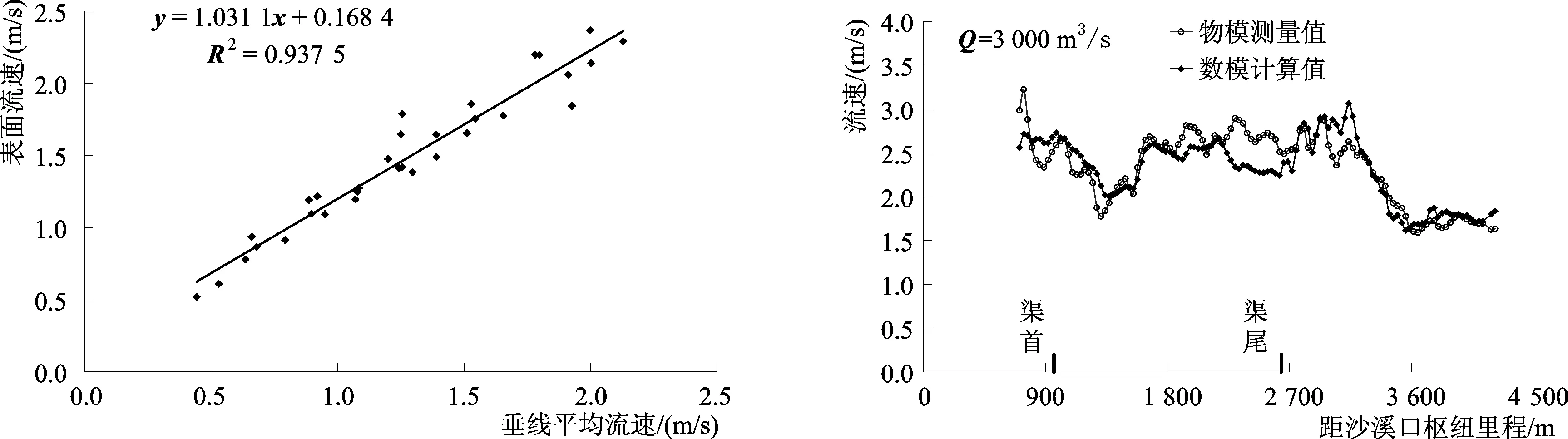
图5 实测垂线平均流速与表面流速关系 Fig.5 Relationship of measured data between depth-averaged velocity and surface velocity图6 近坝段航道物理模型与数学模型流速沿程变化对比图Fig.6 Contrast map of velocity between physical model and mathematical model along the waterway

3.5 复杂碍航水流

利用数学模型和物理模型的流场信息进行航道纵向流速、横向流速和回流流速分析在目前航道整治工程研究中的应用较为广泛，但对于滑梁水、剪刀水这类具有较强动态特性的复杂碍航水流，以往研究中，主要根据物理模型试验来观察流态，利用数学模型进行分析研究的报道较少。

物理模型试验表明，一般情况下，丁坝SJ1因挑流影响斜流偏大；在电站泄流Q≥750 m3/s时，明渠渠顶及丁坝SJ2、SJ3漫流后，因丁坝为斜坡式结构，坝头处坝顶高程较低，丁坝上游产生向明渠内的翻坝水流，航道内的斜流强度较大，最大横向流速可达0.78 m/s。随着流量进一步增大，丁坝及明渠渠顶淹没深度增加，丁坝挑流作用有所减弱；明渠出口处，由于左右侧礁石挑流作用，航道内产生剪刀水，尤以Q=1 000 m3/s、Q≥1 800 m3/s时较为明显，最大横向流速达1.08 m/s。

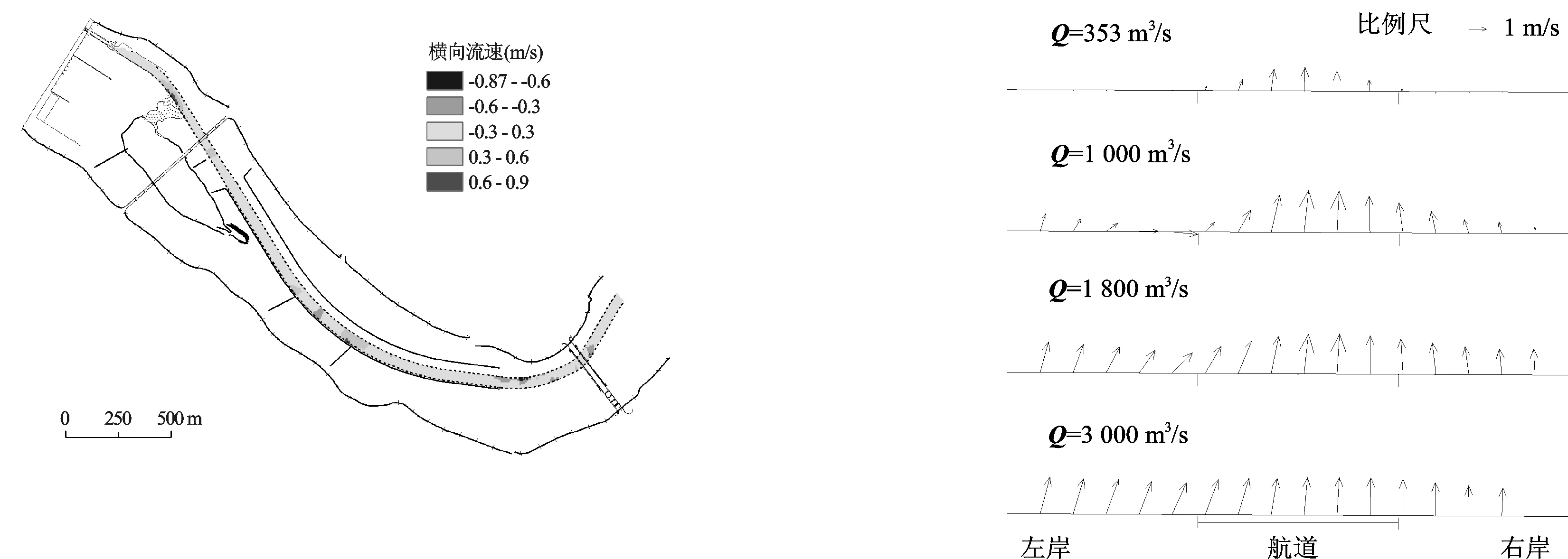
图7 Q=1 000 m3/s时近坝段航道横向流速分布图Fig.7 Transverse velocity distribution of waterway downstream the dam at discharge 1 000 m3/s图8 明渠出口典型断面流速分布图Fig.8 Velocity distribution of typical section near the open channel export

将数学模型计算的航道流速分解成平行与航线的纵向流速和垂直与航线的横向流速(横向流速向左为正，向右为负)，以Q=1 000 m3/s为例(图7)，因丁坝SJ1、SJ2、SJ3挑流影响，在其附近的航道均有明显的横向流速高值区，尤其在丁坝SJ3附近，航道右侧边缘局部流速达0.6～0.9 m/s，与物理模型观测结果基本一致；明渠出口下游，因左右侧水流与经明渠而下的主流交汇，流场较为紊乱，横向流速分布也较不规则，从典型断面(明渠下游150 m)流速分布(图8)来看，航道两侧水流汇入航道较为明显。从滑梁水、剪刀水在各级流量下的强弱变化规律来看，均以电站下泄流量Q=1 000 m3/s最为典型，数学模型通过分析航道纵向流速和横向流速分布揭示的滑梁水、剪刀水等碍航水流规律与物理模型观测结果基本一致。

4 讨论

水工物理模型试验是建立在相似理论基础之上的，只有相似理论所规定的各项相似条件得到满足时，模型水流运动才能同原型水流达到相似[12]。但实际上，物理模型与原型难以做到完全相似，试验过程中，水位、流场等数据也会因采集设备及手段的制约而产生一定的误差。水工数学模型通过建立水流连续性方程和动量方程来描述水流的运动，由于水流运动的复杂性，一些复杂水流现象在机理的认识上还不足，此外，因数学模型一般对整治建筑物进行一定的概化处理，在整治建筑物具体结构型式以及局部流态问题的模拟方面还存在一定的不足。因此，水工物理模型和数学模型均是原型的一种近似，客观上两种模型均存在误差，虽然理想情况两种模型结果趋于一致，但实际的差异常常难以避免的。这也是本文数学模型和物理模型结果出现相似性和差异性的主要原因。

对于一些复杂的水工模型问题，基于两种模型结果相似性的特点，在前期研究中，可以发挥数学模型研究周期短、研究范围不受场地限制、方案修改方便的优势，进行多方案筛选计算，并为物理模型提供边界条件；因两种模型结果存在一定的差异，以及物理模型直观和对于局部工程问题模拟更精确的原因，需要物理模型对数学模型成果进行进一步验证，以提高研究的精度，并进行方案的细部优化。这种数学模型和物理模型相互配合的复合模型研究方法在沙溪口水电站坝下航道整治工程中得到了很好的应用，该方法对于缩短试验周期、节约试验费用具有积极作用。