均质透水丁坝二维水流模拟研究

游立新，许 慧，魏 帅，陈梓偲

(1.中交第二航务工程勘察设计院有限公司，武汉 430060；2.水利部交通运输部国家能源局南京水利科学研究院，南京 210029；3.山东省淮河流域水利管理局规划设计院，济南 250100；4.河海大学，南京210098)

丁坝作为常见的航道整治建筑物之一，其作用主要是整治浅滩、稳定航槽、确保航深。根据透水性能的不同，可分为实体和透水丁坝。实体丁坝坝头处水流分离严重，坝头冲深较大，坝后水流复杂，而透水丁坝具有一定的透水率，可减少坝头水流分离程度和大漩涡的产生，减弱坝头局部冲刷深度[1-3]。此外，透水丁坝具有一定孔隙率，可为鱼类和水生生物提供庇护和栖息环境，有利于生态环境多样化发展，对环境保护起到积极作用。因此，透水丁坝是一种极具发展前景的整治建筑物。常见的透水丁坝有三类：(1)由桩、木头构成的桩柱式丁坝；(2)由铅丝笼或土工织物布包裹粗砂材料构成的丁坝；(3)在实体丁坝(不透水丁坝)中布设过水管。

1 背景

自1970年黄河中下游河道治理开始试用透水丁坝以来，目前全国各大流域的河道治理及主要航道整治工程中均出现有透水丁坝工程。透水丁坝附近水流流动是一个三维问题，表现为坝头集中绕流、下潜流及坝头后方竖轴漩涡这三者在一定弗劳德数范围内相互作用而形成的复杂涡街结构。在实际工程中，往往更关心建坝后大范围水位、流场变化及影响范围，故采用二维水流数学模式已经可以满足实际需要。许多学者模拟了实体丁坝附近二维水流运动[4-11]，而对于透水丁坝，专门的研究则相对较少[12-13]。本文基于正交曲线贴体坐标系下平面二维水流数学模型方程，通过引入通度系数的概念考虑丁坝的透水率，对考虑通度系数后的方程进行离散和求解，并采用水槽试验资料对模型进行了验证。

2 二维数模中透水丁坝的处理

2.1 控制方程组

正交曲线贴体坐标系下，水流运动控制方程式可表示为

水流连续方程

(1)

ξ方向动量方程

(2)

η方向动量方程

(3)

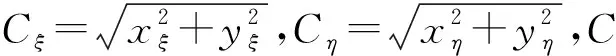
(4)

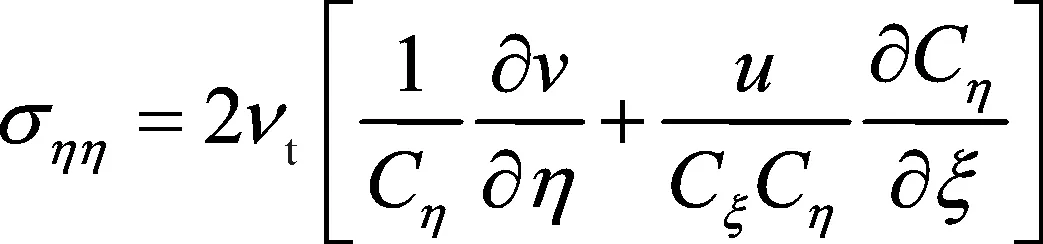
(5)

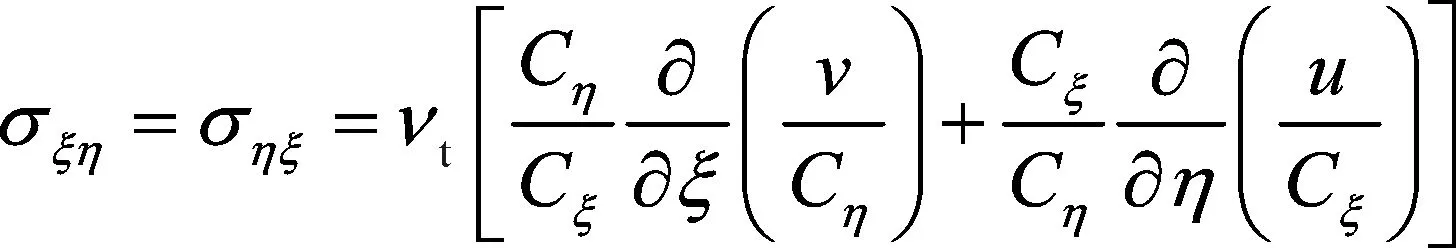
(6)

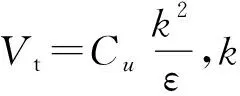
2.2 通度系数概念的引入

相比于实体丁坝，透水丁坝坝体具有一定的透水率。透水率是指坝体透空体积与丁坝体积之比，反映了透水丁坝结构阻水特性，在数值模拟时透水率需作为重要影响参数加以考虑。受戴会超[14]和金忠清[15]用通度系数的概念处理叉管不规则边界的启发，引入通度系数的概念处理透水丁坝。通度系数是指流体可通过区域在整个区域中所占的比例，在计算区域离散化以后，网格单元会有不同的通度系数。通度系数又可分为体通度系数和面通度系数两种[14-15]。体通度系数表示一个单元内流体所占据的体积分数，用PV表示；面通度系数则表示一个单元的一个侧面上可供流体通过的面积分数。对于三维问题，一个控制体有6个面通度系数，用Pe、Pw、Pn、Ps、Pt、Pb表示；对于二维问题，一个控制体有4个面通度系数，分别用Pe、Pw、Pn、Ps表示。

由于丁坝的宽度跟计算区域长度相比较小，完全可以将丁坝概化为占有一个网格单元宽度的一列控制体。各水力要素布置如图1所示。

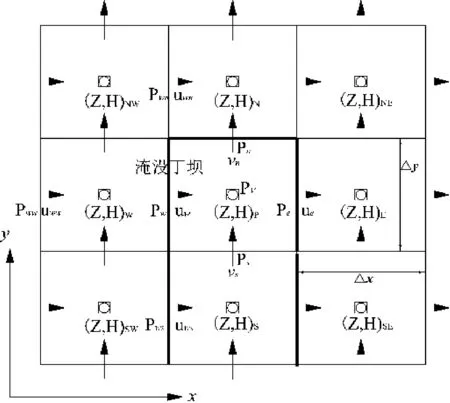
图1 水力要素网格布置图Fig.1 Layout of hydraulic elements grid 注：○表示水位Z节点位置，→表示u节点位置，↑表示v节点位置，□表示水深H节点位置。

丁坝透水以后，有效阻水面积减少，阻水作用降低。假设丁坝在某一方向的透水率为φ，则丁坝有效阻水面积=丁坝投影断面面积×φ。考虑沿水流方向和垂直水流方向透水率一致的情况下，则

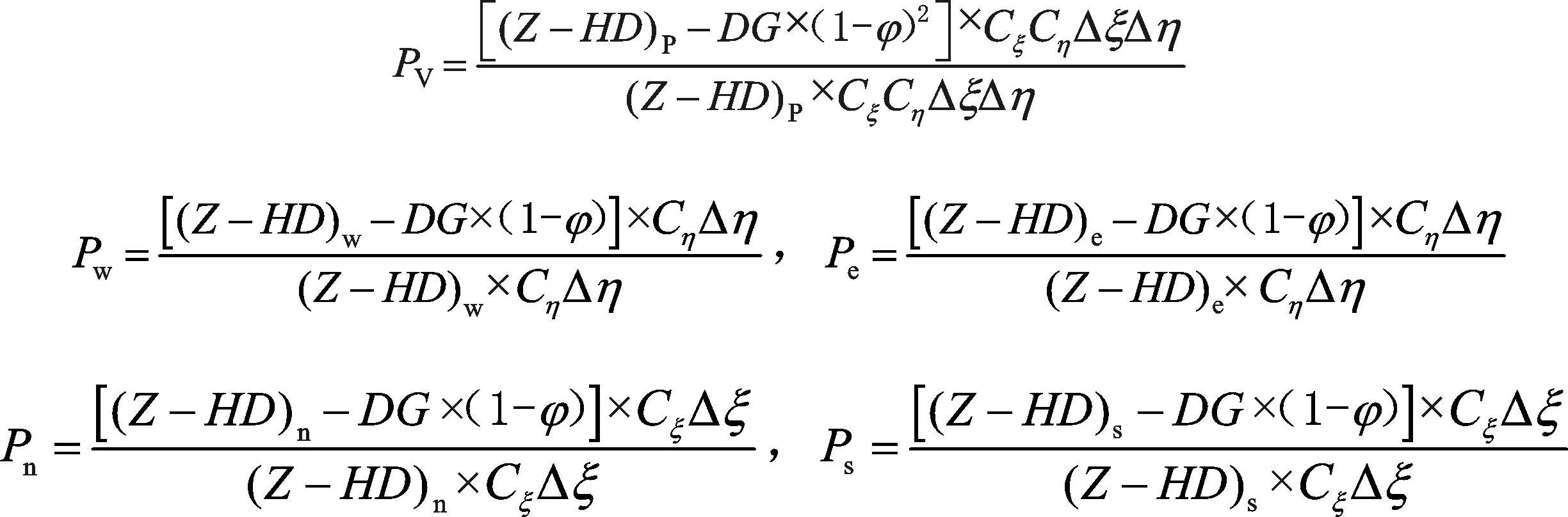
(7)

式中：DG表示坝高，(Z-HD)P、(Z-HD)w仍代表当地网格中心控制点和网格线上水位与地形差值，其余方向类似定义。上式对淹没透水丁坝也是适用的，丁坝坝顶以上部分完全通水，以Pw为例，通度系数随水位Z的抬高而增大。

2.3 考虑通度系数后的方程离散和求解

将通度系数视作空间分布的变量，在交错网格中，体通度系数PV与其他变量布置在主控制体中，面通度系数Pe、Pw、Pn、Ps与速度分量一起布置在主控制体的相应侧面上(图2)。

图2 通度系数和其他变量在 交错网格中布置Fig.2 Layout of block up coefficient and other variables in staggered grids

水流运动方程组(1)、(2)、(3)可写成如下通用微分方程

(8)

式中：Φ表示通用变量， Γ为广义扩散系数，S为源项。

根据守恒定律，推导单元离散方程时应在相应的体积分上乘以该单元的体通度系数PV；在相应的面积分上乘以相应交界面的面通度系数Pe、Pw、Pn、Ps，由此离散方程变为

(9)

式中：

(10)

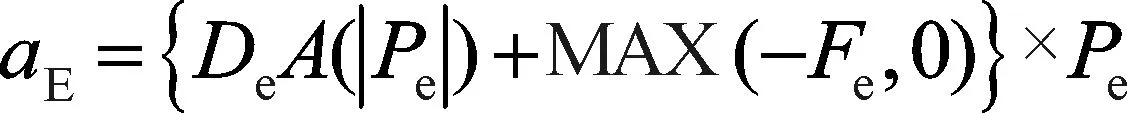
(11)

(12)

(13)

(14)

(15)

各控制面上对流、扩散强度及派克里特数Fe、De、Pe、Fw、Dw、Pw、Fn、Dn、Pn、Fs、Ds、Ps表达式见文献[10]。

采用水位校正法SIMPLER程式求解耦合水位-速度场，求解代数方程组时仍采用交替方向隐式迭代法，反复迭代直至流场结果满足精度，通过控制水位校正方程中质量源项的最大值来确定收敛情况。

3 模型验证

3.1 水槽布置

采用王振[16]2012年铅丝笼透水丁坝定床水槽试验结果对采用通度系数法的平面二维数学模型进行验证。试验在总长为20 m，宽0.5 m，高为0.44 m的矩形玻璃水槽中进行，试验段选取在水槽中间6～12 m范围内。经率定水槽综合糙率n取0.009 9，进出口水位流量条件由三角堰和尾门控制，其中进口流量设置为0.015 m3/s，出口水深为0.065 m。沿水流方向在水槽左侧距进口9 m处布置正挑透水丁坝模型，丁坝尺寸长L=0.15 m，宽B=0.05 m，坝高H0=0.10 m。铅丝笼丁坝沿水流方向和垂直水流方向透水率一致，试验测得透水率均取20%。丁坝平面位置及测量断面布置如图3所示，每个断面布设5～11根垂线。

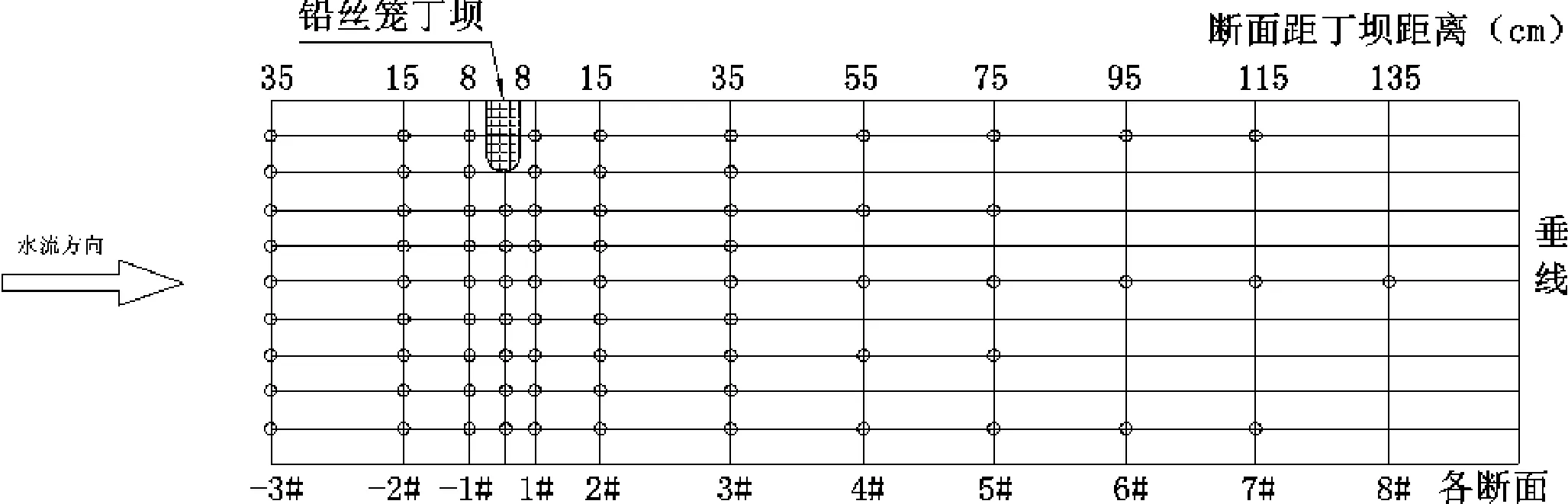
图3 丁坝平面布置和测量断面布置Fig.3 Plane layout of spur dike and survey section

3.2 流场和水位对比

图4 透水丁坝附近平面流场图Fig.4 Flow field near the permeable spur dike

透水丁坝附近区域流场如图4所示。由图可见，透水丁坝作用后的水流流态与实体丁坝类似，坝头形成分离流，坝后形成回旋流。在坝轴断面，由于丁坝具有一定的透水性，少量的水通过坝体间的空隙流向下游，但流速较小；在坝头，由于丁坝的束窄作用使坝轴断面单宽流量增大，主流流速增大；在丁坝轴线下游侧，由于丁坝的影响，在坝后形成回流区，主流由于惯性作用进一步收缩，流速继续增大，到最小收缩断面处达到最大，随后主流扩散，在一定距离后重新趋于均匀。

丁坝上下游各个断面的流速(u/u0)、水深(h/h0)验证见图5和图6，其中u、h为测点流速、水深；u0、h0为无坝时断面平均流速、水深；坐标原点设置在透水丁坝坝根处，x轴方向为水流运动方向，y轴方向为垂直水流方向，并指向河内。由图可见，计算值和实测值符合较好，模型能够反映透水丁坝作用影响下流速和水位分布。在丁坝上游，越靠近丁坝，丁坝侧水面逐渐壅高，流速减小，丁坝对岸侧流速则相应增加，丁坝的阻水作用逐渐增强；当水流到达丁坝位置时，丁坝束窄作用最强，比降和流速迅速增大，丁坝处水面出现明显降落；水流流过丁坝后，主流流速仍有继续增大趋势，坝后出现与水流流向相反的流速，形成回流，随着断面向下游移动，主流逐渐扩散到无丁坝影响的断面水流状态。通过验证，说明采用通度系数可较好模拟沿水流方向与垂直水流方向透水率一致的丁坝附近水流运动。

图5 透水丁坝断面流速计算与实测对比Fig.5 Comparison between calculation and measurement of flow velocity in permeable spur dike section

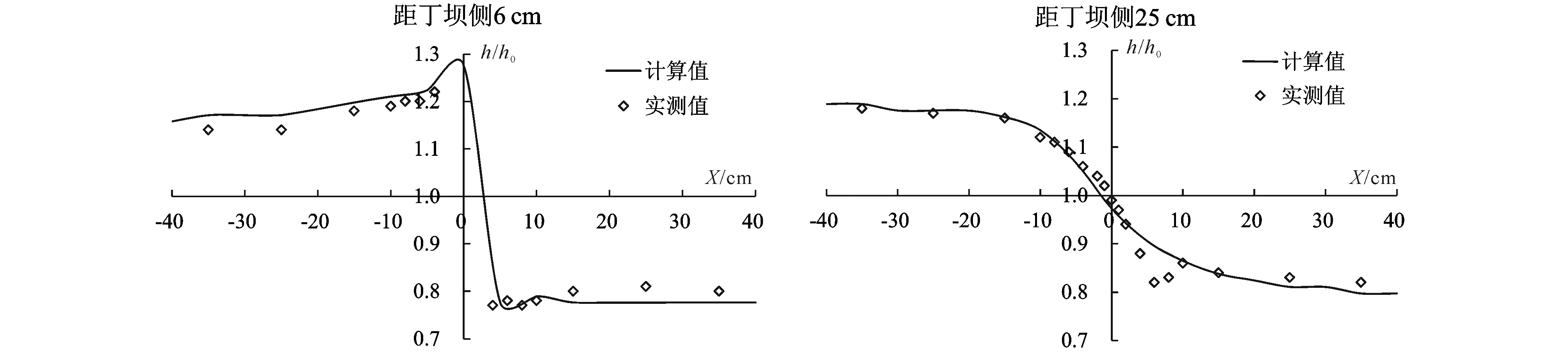
图6 透水丁坝纵向水面线计算与实测对比Fig.6 Comparison between calculation and measurement of longitudinal water surface profile of permeable spur dike

4 不同透水率对丁坝附近水流影响

图7 不同透水率时丁坝附近流场图Fig.7 Flow field near spur dike with different permeability

不同透水率的丁坝对坝后回流的影响是不同的，其保护范围也不一样。为研究不同透水率对丁坝附近流速分布影响，在前述3.1节水槽和丁坝尺度基础上，以不透水丁坝(透水率为0%)作为对照，模拟5组不同透水率(0%、20%、40%、60%、80%)工况下丁坝附近流场。

当透水率为0时，丁坝上游流速有较明显的减小，下游坝后有明显的回流区；随着透水率逐渐增加，丁坝阻水作用减弱，相应地透过坝体的水流增加，与坝后水流相互碰撞，导致坝后回流区域逐渐缩小，流速增大；当透水率增至80%时，丁坝上游断面流速分布均匀，坝后回流现象基本消失。

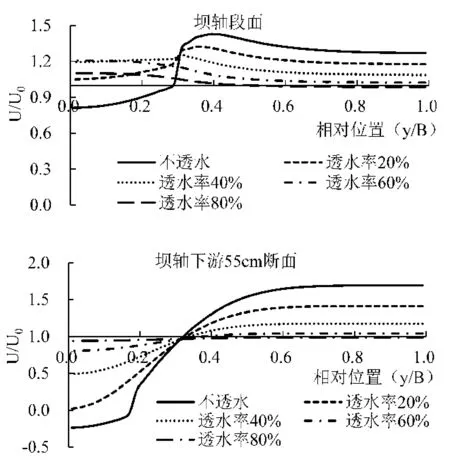
图8 不同透水率时丁坝附近断面 流速对比图Fig.8 Comparison of cross-sectional flow velocity near spur dike with different permeability

由丁坝轴线断面流速分布可看出(图8)，不同透水率时流速比(其中U0为无坝时流速，横坐标为距丁坝侧壁面的相对位置)均大于1，原因是透水率增加后，一部分流量通过坝体间隙穿过，坝头流速比下降。可见，丁坝透水后能有效降低坝头流速，缓解坝头冲刷现象。

由坝下游典型断面流速分布可看出(图8)，丁坝透水率越低，回流区长度越长，回流区域越大；不同透水率时丁坝对岸侧流速比差别比较明显，流速比为1.7左右；透水率较大时流速比维持在1.1左右，说明随透水率增加，丁坝挑流作用逐渐减弱，过坝后的水流逐渐趋于均匀。

5 结语

(1)基于正交曲线贴体坐标系下平面二维水流数学模型，引入通度系数的概念考虑丁坝的透水率，并对考虑通度系数后的方程进行详细的离散推导和求解。

(2)采用已有的水槽试验资料，对模型进行了初步验证，模拟透水丁坝作用后的流场和水位场，结果表明计算和实测符合较好。丁坝透水率越大，阻水缓流作用越弱，丁坝束窄区域主流区流速降低，坝轴及下游各断面流速变化幅度减小；坝后回流范围缩小，流速与主流区流速趋于均匀。

(3)受水槽试验限制，目前仅模拟了各方向透水率相同的丁坝附近水流运动，下一步将考虑对各部位透水率不同的丁坝水流进行模拟对比。