基于DSP Builder的快速整数离散余弦变换的实现
2019-01-18梁东云
梁东云
(商洛学院 电子信息与电气工程学院,陕西 商洛 726000)
离散余弦变换(DCT)是一种常用的信号处理变换,具有很强的“能量集中”特性,而且当信号具有接近马尔科夫过程的统计特性时,DCT的去相关性接近K-L变换的性能,因此它被广泛应用于视频信号处理和音频信号处理等领域[1-3]。常见的H.264视频编码就利用了整数DCT[4-5]。实际应用中,相关算法的实现需要硬件的支撑。现代电子设计自动化(EDA)技术的迅速发展,使得常见算法可以通过硬件描述语言并利用现场可编程门阵列(FPGA)的逻辑资源实现,但代码编写、硬件调试比较复杂,开发周期长[6-8]。使用调试好的知识产权(IP)核可显著减小工作量,但许多IP核需要单独购买[9]。本文利用DSP Builder平台,在Simulink工作环境下采用图形模型构建整数DCT的蝶形运算模型,并对其进行仿真。由于该模型将多个EDA工具联合起来,避开了复杂的代码设计,因此降低了开发难度。
1 整数DCT变换
传统二维DCT及其逆变换如下所示[3]:
在H.264频频编码过程中,采用了4×4整数DCT,在不损害图像精度的前提下,减少了数据运算量,避免了传统浮点运算带来的数据失配问题。4×4整数DCT的基本变换如下所示[5]:
(1)
可等效为
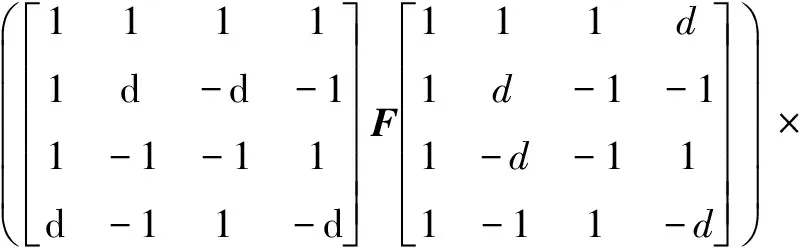
(2)


(3)
可将式(3)的二维变换改造成2个一维变换。先对数据块矩阵每一行做一维整数DCT,然后再对结果的每一列进行一维整数DCT。每一次一维变换可以借助蝶形算法来快速完成,可减少运算量[10]。一维蝶形运算如图1所示。
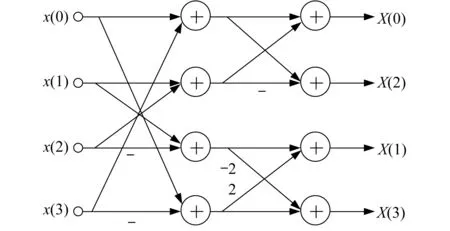
图1 一维整数DCT蝶形运算Fig.1 One-dimensional integer DCT butterfly operation
图1中,x(0)~x(3)代表蝶形运算的输入数据,X(0)~X(3)代表蝶形运算的输出结果。相对于式(3),蝶形运算减少了计算量。然而,利用代码实现计算仍然比较复杂。借助DSP Builder平台,可以构建整数DCT运算的图形化模型,避免繁杂的代码编写。
2 模型设计
本文中搭建的一维整数DCT蝶形运算的DSP Builder模型如图2所示。图2中,In0~In3代表输入数据,Out0~Out3代表输出数据。将该模型封装为子系统,构建每一行(或列)的运算模型,然后将行、列运算模型级联,形成完整的二维整数DCT运算结构。该运算结构还不能直接用于测试,外加相应的数据输入及数据输出显示模块,才能形成顶层测试模型。

图2 一维整数DCT蝶形运算的图形模型Fig.2 Graphical model of one-dimensional integer DCT butterfly operation
3 仿真测试
含有输入输出数据的顶层测试模型如图3所示。
图3中x00~x33代表原始图像数据,Display模块显示输出结果,Subsystem和Subsystem1为一维整数DCT蝶形运算封装后的子系统。令4×4原始图像矩阵
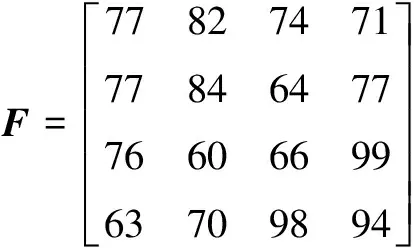
仿真测试后从Display模块中显示变换后图像矩阵,如下所示:
经Simulink平台仿真后,运行“Signal Complier”可以将模型转换为硬件描述语言,并产生测试向量文件[10]。利用Modelsim平台对测试向量文件进行仿真,仿真输出数据如图4所示。
图5为直接在Matlab平台中运行代码的结果。通过对比可见,3种方法仿真结果一致,说明本文模型能够完成二维整数DCT的快速蝶形运算,并可通过后续硬件实现。综合后的硬件电路图较大,本文中略过。
4 结语
本文利用DSP Builder和Simulink平台,对H.264视频编码过程中常用的整数DCT进行了模型构建与仿真。本文以4×4整数DCT的快速蝶形运算为例,实际中可很容易地推广至8×8、16×16等分块情况。同时,整体设计是基于模型的方式,因此减少了代码编写的工作量。在实际的综合电子实训教学过程中,将数字信号处理等课程内容综合起来,逐步推广模型化电路设计方式,使学生能够快速地体会到信号处理相关理论的硬件模型实现。

图3 顶层测试模型Fig.3 Top-level test model
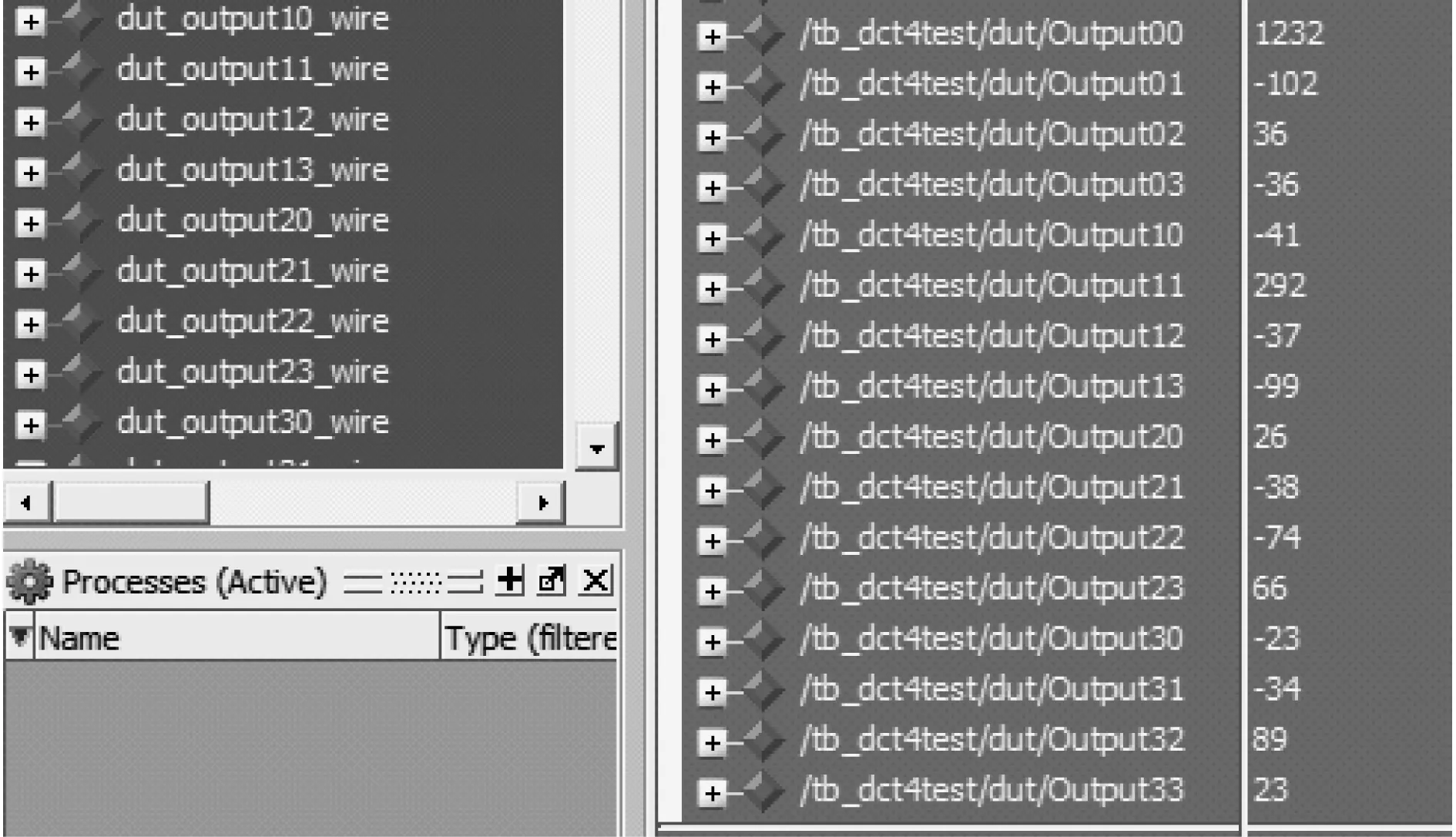
图4 Modelsim仿真结果Fig.4 Modelsim simulation results
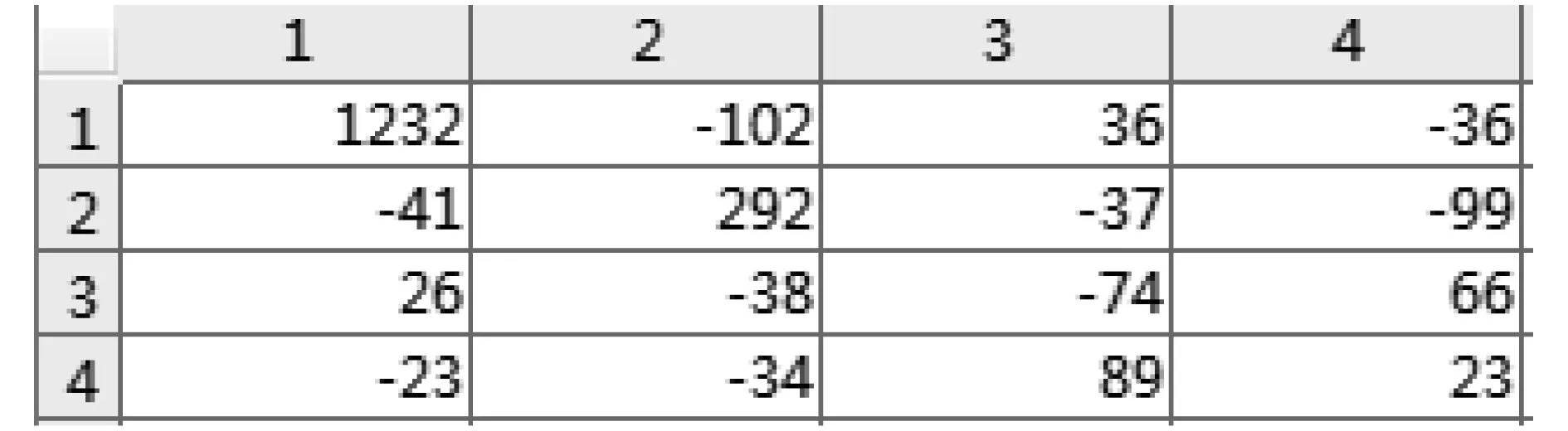
图5 Matlab仿真结果Fig.5 Matlab simulation results
