区间二型模糊控制器设计

王新超

(中国能源建设集团江苏省电力设计院有限公司,江苏 南京 211102)

Zadeh[1]提出了基于一型模糊集合的一型模糊控制器,随着控制理论的发展该控制器得到了广泛应用,目前主流的模糊控制系统都是基于该控制器展开。

在实际应用中,工业控制流程变得越来越复杂,各类不确定性如噪声测量、执行器特性等,都会使系统的输入和输出发生变化。针对这种情况,Zadeh[2]又提出了二型模糊集合,将隶属度进一步模糊化。基于二型模糊集合的二型模糊系统,可以对语言和数据的不确定性进行处理,进而可以处理模糊规则的不确定性[3]。在很长一段时间内,由于二型模糊集合运算的复杂性,导致二型模糊逻辑理论的发展相对较为缓慢。Mendel等[4-7]将二型模糊集合的次隶属度都定为1,从而大大简化了区间二型模糊集合运算,使得区间二型模糊逻辑系统得到了较快发展。

常用的区间二型模糊集合的降阶算法有Karnik-Mendel(KM)[8]算法、enhanced Karnik-Mendel (EKM)[9]算法等,这些算法都需要通过迭代来寻找降阶的端点,取平均值后得到降价结果。在实际控制中,迭代过程比较耗费时间。

本文采用直接降阶算法来设计模糊控制器。该算法避免了KM等算法的迭代过程,在得到模糊规则的首隶属度上、下限后,根据首隶属度上、下限和模糊规则的后件参数计算控制器输出的2个端点,取平均值后得到控制器的实际输出。

1 区间二型模糊控制集合

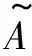
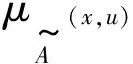
(1)

区间二型模糊集合简化了二型模糊集合的次隶属度,并将其定义为1,如下所示:

∀u∈Jx∈[0,1]}

2 区间二型模糊控制系统

区间二型模糊控制系统与传统模糊控制系统结构类似,区别在于模糊推理后区间二型模糊控制器要增加一个降阶过程,具体结构如图1所示。图1中,r表示输入,y表示输出。

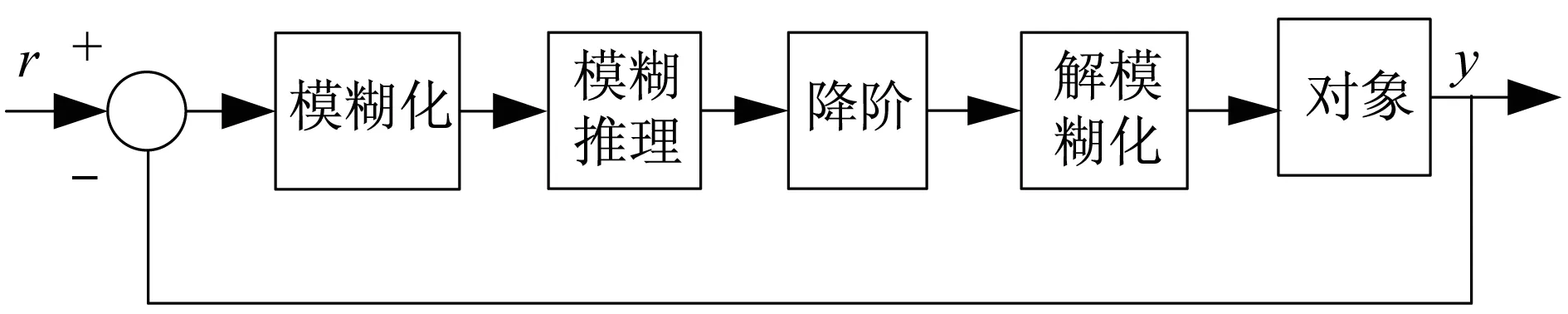
图1 区间二型模糊控制器结构Fig.1 Structure of interval type-2 fuzzy controller

由于T-S模糊模型具有独特的规则形式以及易于与其他控制方法相结合的特点,本文采用T-S模糊控制器进行被控对象的控制。T-S模糊控制器的第l条规则如下所示:

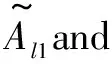
该规则中:clp是后件参数,为精确值;yl是第l条规则的输出,为精确值;Alp是前件参数,为二型模糊集合;x1～xp是状态参数。

通常区间二型模糊控制器的输入选择误差e和误差的变化量Δe。如果误差和误差的变化量各自选择的模糊集合个数分别为N1和N2,模糊规则数目就为N1N2。二型模糊控制器增加了控制器部分的模糊性,因此增强了整个模糊控制系统处理不确定性的能力。

3 本文算法

本文中对区间二型模糊控制器误差和误差的变化量分别定义2个模糊集合,那么一共有4条规则,如下所示:

控制量增量解的模糊化结果如下所示:

4 仿真实例

选取一阶迟延对象,其传递函数如下所示:

式中:K代表比例增益;T代表积分时间;τ代表迟延时间。本文中,τ=2.5 s,采样周期为0.1 s。本文仿真是对一阶迟延对象做单位阶跃响应,因此图2～5的纵坐标没有单位。图2～5中,T1表示一型模糊控制系统,IT2KM表示使用KM算法的区间二型模糊控制系统。

4.1 仿真实例1

对象参数为:K=1,T=10。仿真实例1的阶跃响应如图2所示。

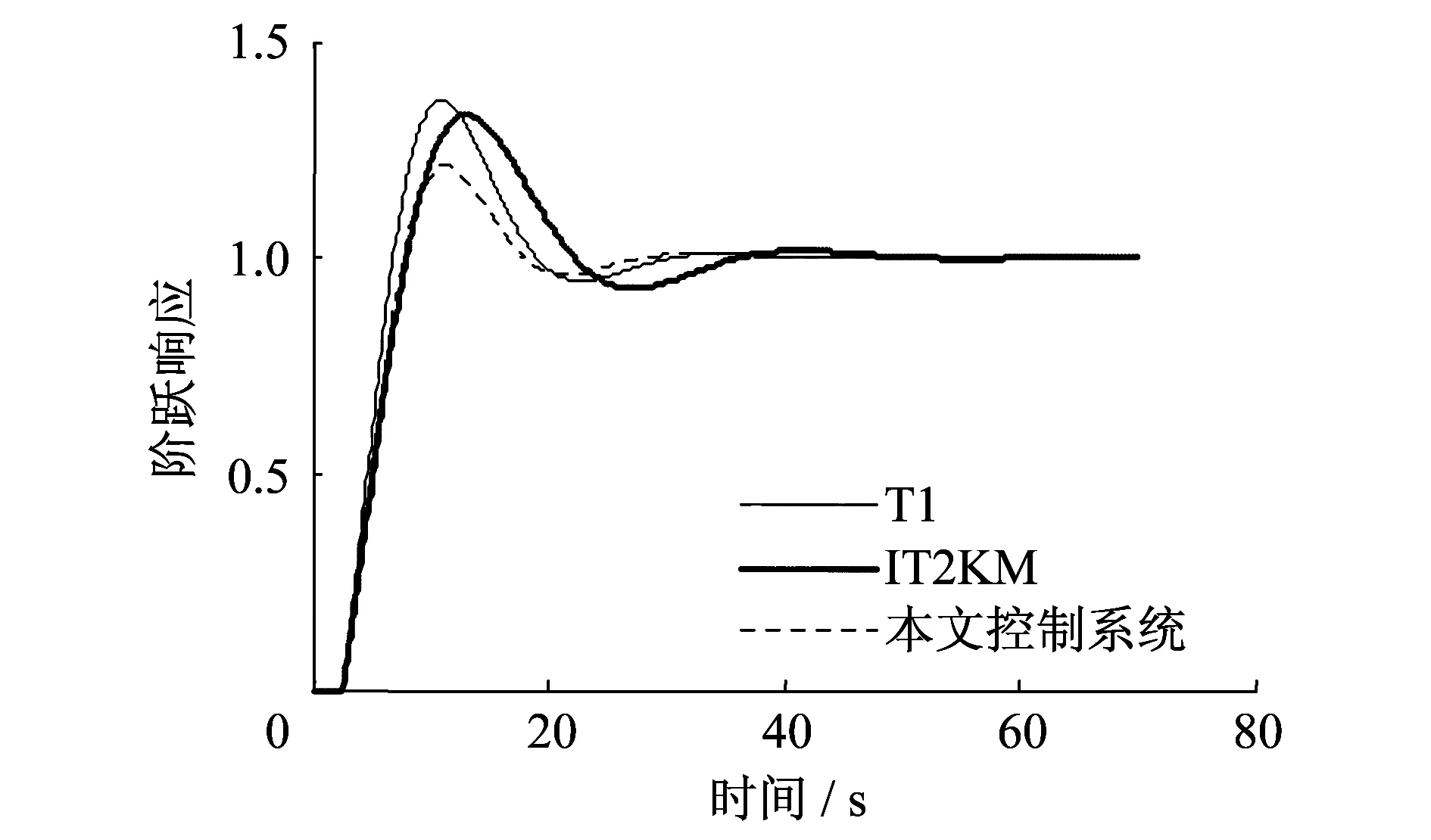
图2 一阶系统阶跃响应(K=1,T=10)Fig.2 Step response of the first order system(K=1,T=10)

4.2 仿真实例2

对象参数为:K=1,T=20。仿真实例2的阶跃响应如图3所示。

图3 一阶系统阶跃响应(K=1,T=20)Fig.3 Step response of the first order system(K=1,T=20)

4.3 仿真实例3

对象参数为:K=5,T=10。仿真实例3的阶跃响应如图4所示。

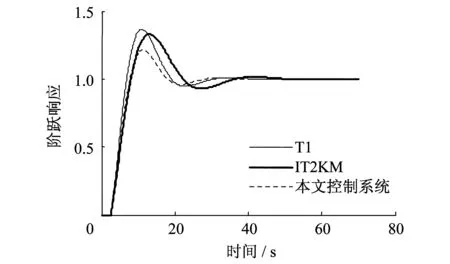
图4 一阶系统阶跃响应(K=5,T=10)Fig.4 Step response of the first order system (K=5,T=10)

4.4 仿真实例4

对象参数为:K=5,T=20。仿真实例4的阶跃响应如图5所示。

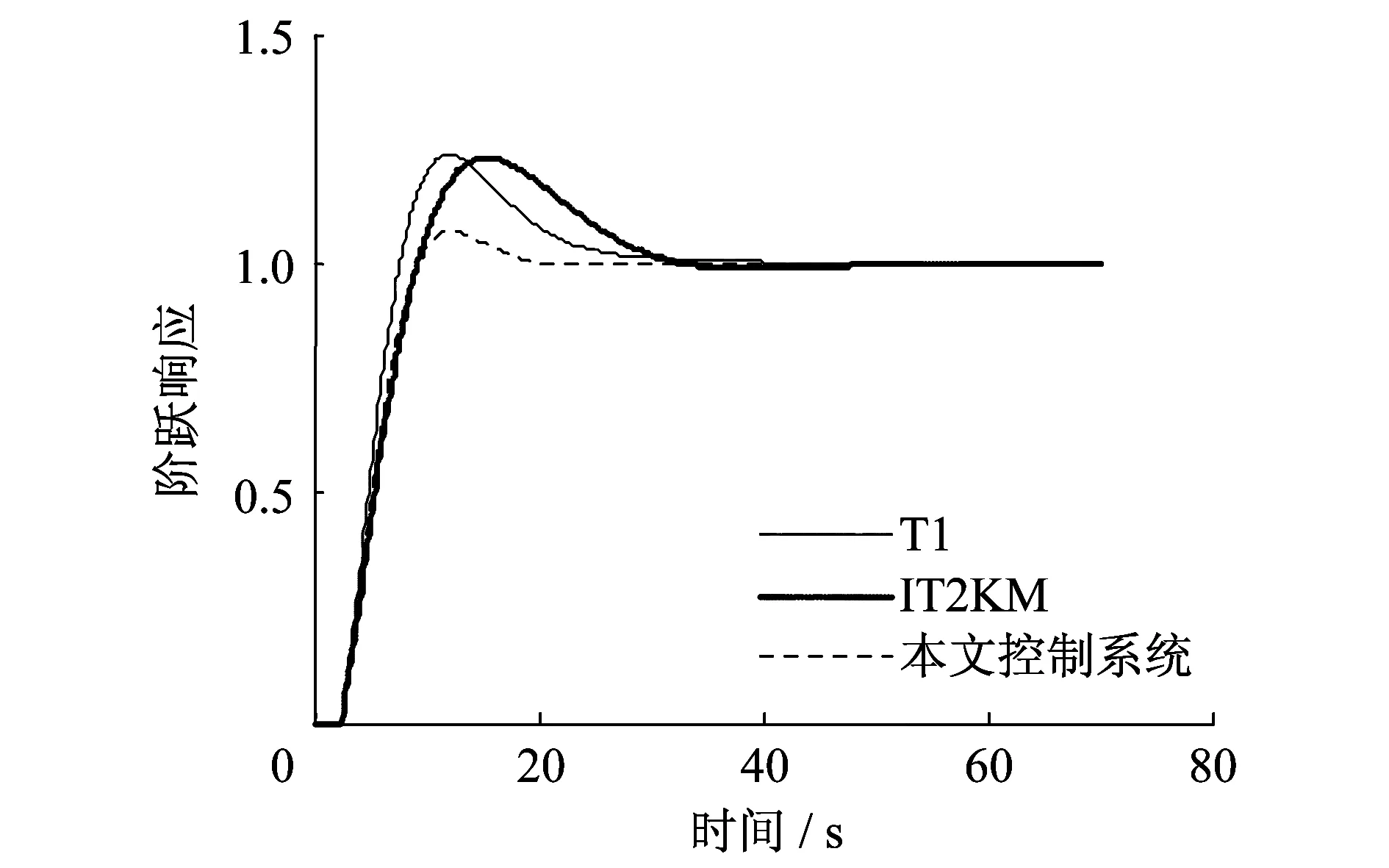
图5 一阶系统阶跃响应(K=5,T=20)Fig.5 Step response of the first order system (K=5,T=20)

5 结语

针对传统模糊控制器在解决不确定性方面的缺陷以及基于KM算法的区间二型模糊控制器效率低下的问题,采用直接降阶算法,设计了区间二型模糊控制器。该控制器利用区间二型模糊集合的隶属度上、下限以及模糊规则的后件参数来计算控制器的输出,避免了KM等算法的迭代过程,保证了控制器的实时性。对一阶迟延对象在4种不同参数下的仿真结果表明,本文控制系统具有较好的控制效果。