基于Matlab/Simulink的浮空飞行器压力控制系统仿真
2019-01-18孙银娣
孙银娣, 王 风, 周 雷
(中国特种飞行器研究所,湖北 荆门 448035)
本文研究的浮空飞行器主要指无人动力飞艇(下文简称飞艇),其压力控制系统通过控制和调节内部各气室的压力,从而保证不同飞行状态下气囊内外压力差稳定在一定范围内,维持气囊良好的刚度和气动外形,确保飞艇正常工作。当飞艇的气体压力超过设定的最高压力时,气囊压力控制系统的排气装置工作,从气囊内排出足够的空气,使气体压力不超过气囊工作压力的上限;当飞艇的气体压力低于设定的最低压力时,气囊压力控制系统的供气增压装置工作,将外界空气充入飞艇气囊中,使气体压力不低于气囊工作压力的下限[1]。
本文以某飞艇的简化模型为仿真对象,首先建立了气囊压力控制系统充排气数学模型,并在此基础上搭建了通用的气囊压力控制仿真系统,模拟飞艇在升空和回收过程中气囊压力变化全过程。最后,对飞艇升空过程中压力调节全过程进行了仿真分析。
1 气囊压力控制系统数学模型
1.1 气囊构型
飞艇气囊分为主气囊(氦气囊)和副气囊(空气囊)。气囊压力控制系统的主要控制变量是:主气囊内氦气的绝对压力与紧近气囊大气压的压力差,即主气囊压力;副气囊内空气的绝对压力与紧近气囊大气压的压力差,即副气囊压力。本文仿真的某飞艇采用单主副气囊结构、双风机和双阀门装置。
1.2 气囊气体状态模型
1.2.1数学建模的几点假设
(1) 飞艇内的气体均为理想气体,飞艇内充装空气和氦气。在飞艇的整个工作过程中,内部气体的压力都不高并且内部气体的温度远离它们的临界参量。
(2) 飞艇体积在飞艇整个运行过程中保持不变,在微小的压力变动下,囊体弹性变形量忽略不计。
(3) 飞艇内部的气体系统在飞艇升空和回收过程中的热力学变化为准静态过程。
(4) 计算过程中,升降过程假设为气囊内部气体温度时刻保持与外界大气温度相同。
(5) 不考虑透氦率的影响。
1.2.2气囊气体状态方程
根据第1.2.1节的假设分别列出飞艇主副气囊内理想气体的状态方程,如下所示:
PHeVHe=mHeRHeTHe
PairVair=mairRairTair
式中:PHe为主气囊内氦气压力;VHe为主气囊内氦气体积;mHe为主气囊内氦气质量;RHe为主气囊内氦气的气体常数;THe为主气囊内氦气温度;Pair为副气囊内空气压力;Vair为副气囊内空气体积;mair为副气囊内空气质量;Rair为副气囊内空气的气体常数,Tair为副气囊内空气温度。主副气囊内气体密度分别为
主副气囊内气体体积关系为
Vair=VA-VHe
式中:VA为气囊总体积。
飞艇在升空和降落过程中气囊内气体压力状态变化阈值及最大升空高度很大程度上受气囊构型及初始充氦量、初始气体状态约束。在Matlab/Simulink模型里气囊构型及初始气体状态封装在初始化模块内。初始构型参数如表1所示。
根据压力差定义,主气囊初始绝对压力PHe0=ΔPHe0+Patm0,其中Patm0为飞艇初始飞行高度处的大气压力,则
式中:Pa为平均海平面的大气压力;Ta为平均海平面的大气温度。由此可以推导出初始充氦质量
表1气囊压力系统初始构型参数
Tab.1Initialconfigurationparameterofballonetpressuresystem

参数符号参数意义单位系统类别VA0初始气囊总体积m3气囊结构Sn0初始副气囊底面积m2气囊结构φHe0初始充氦体积分数压力系统H0初始海拔高度m压力系统ΔPHe0初始氦气压力差Pa压力系统AV阀门的流量面积m2执行机构Cd阀门的流量系数执行机构
式中:VHe0和THe0分别表示主气囊内初始氦气体积和温度。
飞艇在升空和回收过程中任意时刻t,主气囊气体状态模型为
不考虑透氦及应急放氦的前提下,mHet=mHe0。根据第1.2.1节假设,得出以下关系式:
THet=Tairt=Tatmt
Tatmt=288.15-0.006 5Ht
VHet=VA-Vairt
ΔPHet=PHet-Patmt
式中:Tatmt为t时刻飞艇飞行海拔高度处的大气温度;Ht为t时刻飞艇的飞行高度;ΔPHet为t时刻氦气与大气的压力差。
主气囊压力是本文气囊压力控制系统的被控量,系统控制的目标是将ΔPHet保持在规定的安全压力差范围内。在某一飞行高度,ΔPHet一般维持在某一恒定值,由气囊压力控制系统上级控制器给出控制指令。
t时刻主副气囊压力差
Δρ≈ρatm-ρHe
ΔPairt=ΔPHet+ΔPair-Het
式中:Sn为副气囊底面积;ρatm为大气密度;ΔPairt为t时刻副气囊压力差。
在理想气体的假设下,建立了不依赖飞艇飞行状态的气囊气体状态系统通用数学模型,该模型能够较准确地反映气囊内实际气体系统的气体特性。在Matlab/Simulink环境下求解气囊气体压力系统气体状态的过程实际上为解非线性方程合理解的过程。与飞艇其他分系统相比,气囊压力控制系统的状态很大程度上依赖于初始气囊内充气状态及气囊构型等初始状态条件。模型解算后输出主副气囊的压力、温度、密度等状态量,并反馈至气囊压力控制系统控制器,形成闭环控制。
1.3 执行器充排气数学模型
气囊压力控制系统执行器主要是阀门和风机[2]。空气阀排气的数学模型如下所示:
式中:qVair排为空气阀排气体积流量;Vair排为空气阀排气体积;ΔPair为副气囊压力差。
根据采集到的飞艇气囊压力差、温度及当前的飞行高度,通过数据样条插值计算得到风机充气流量。风机向副气囊充气的数学模型如下所示:
qVfan充=f(ΔPair,H,Tair)
式中:qVfan充为风机充气体积流量;Vair充为风机向副气囊充气体积;H为飞行海拔高度。
2 气囊压力控制系统仿真设计
气囊压力控制系统仿真模型均在Matlab/Simulink环境下建立,利用Simulink模型库及S-Function函数编写系统内各部件模型[3]。Matlab/Simulink环境下气囊压力控制系统非线性仿真结构如图1所示。系统仿真模型包含飞艇气囊压力系统模型、控制律模型、执行机构模型、放大器模型、传感器模型等。

图1 气囊压力控制系统仿真模型Fig.1 Simulation model for pressure control system of ballonet
2.1 气囊压力系统仿真模型
在第1节数学模型的基础上建立飞艇气囊压力系统仿真模型,通过Simulink模型库模块搭建而成,如图2所示。图2中,VH表示上升速度。
2.2 控制律仿真模型
控制逻辑模块主要用于执行机构(风机和阀门)工作启停的控制,通过对气囊充排空气使气囊压力保持在安全范围内。根据上述逻辑控制关系,建立气囊压力控制系统控制律模块的仿真模型,如图3所示。
2.3 执行机构仿真模型
执行机构模型包括风机模型和阀门模型两部分,如图4、5所示。风机模型由S-Function函数编写插值程序得出。

图2 气囊压力系统Simulink仿真模型Fig.2 Simulation model for ballonet pressure system based on Simulink

图3 控制律Simulink仿真模型Fig.3 Simulation model for control law based on Simulink
3 仿真分析
采用压力控制系统仿真模型来模拟飞艇上升过程中气囊压力控制系统工作仿真结果,如图6~9所示。图8中,对于风机和阀门状态,1表示“开”,0表示“关”。设定飞艇上升速度很快稳定在2.5 m·s-1,上升至约3 000 m高度。

图4 风机Simulink仿真模型Fig.4 Simulation model for fans based on Simulink

图5 阀门Simulink仿真模型Fig.5 Simulation model for valves based on Simulink
从仿真结果可以看出:升空过程中,飞艇气囊能够在要求的安全压力范围内正常工作,其压力变化规律基本符合实际情况。升空过程中压力控制主要由阀门排放副气囊内的空气,将气囊压力差稳定在设定的值域范围内,此时风机不工作。副气囊排气量情况正常,并且基本无充气现象。由此可见,仿真模型、控制逻辑可靠。另外,不同的上升速度下阀门和风机的工作时间会有所不同。综上所述,本文建立的压力系统数学仿真模型能够较好地模拟飞艇压力控制系统的工作过程。
4 结语
飞艇气囊压力控制仿真系统采用一体化设计原则,实现了压力控制系统的全数字仿真,为半物理仿真试验提供了设计基础。仿真结果表明,仿真模型能够准确模拟升空和回收过程中飞艇气囊压力控制系统的工作状态。

图6 上升过程主副气囊压力差及高度变化规律Fig.6 Change of pressure difference between primary and secondary ballonets and altitude when airship is rising
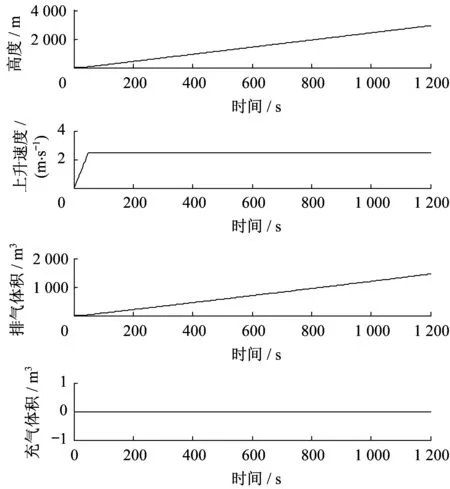
图7 上升过程气囊排充气体积Fig.7 Exhaust volume and inflated volume of ballonet when airship is rising

图8 上升过程阀门与风机工作状态Fig.8 Working status of valve and fan when airship is rising

图9 上升过程主副气囊体积Fig.9 Volume of primary and secondary ballonets when airship is rising
