边海防独立微电网系统优化配置方法

纪秀美, 闫玉铎

(中国人民解放军31002部队,北京 100094)

目前我国广大的边海防地区难以实现与大电网互联,保障这些地区电力的有效供应是政府和部队亟待解决的问题之一。在边海防地区,传统供电方式就是柴油发电机供电,但是传统供电方式对柴油的补给能力有较高要求,运输和补给成本较高,对当地的环境保护也产生了较大压力,而且单一能源的供电方式存在可靠性隐患。随着可再生能源发电和微电网技术的逐步成熟并推广应用,采用以可再生能源为主、柴油发电机为辅的多能源供应形式正成为边海防地区供电的重要发展方向[1-5]。合理利用边海防地区的自然资源,协调配置储能和分布式电源的容量以满足负荷需求,已成为边海防地区独立微电网规划设计领域的核心课题。

文献[6]中以年均投资费用最低为目标,考虑微电网系统的运行约束条件,构建了含风光储独立供电系统的分布式电源优化配置模型。文献[7]中提出了一种风光储容量优化配置模型,该模型综合考虑了风光资源的随机性和机组强迫停运对微电网运行的影响。文献[8]中以孤岛微电网的优化配置问题为基础,采用分时优化方法对并网运行时的储能进行修正。文献[9]中以总成本最小化为目标进行微电网容量优化配置,将供电可靠性作为约束条件或以停电损失补偿成本的形式体现在目标函数中。

本文根据光伏、风机发电分布式电源特性,考虑海岛微电网对供电的高可靠性要求,以年均运行投资成本为优化目标确定系统配置。

1 系统经济性模型

1.1 目标函数

以系统运行年限内的年均等值综合成本来评估系统经济性。经济性目标函数

f(X)=R(r,L)Ccap+Cf+COM+Cc

式中:f(X)为经济性目标函数,表示系统年均总成本;R(r,L)为年均资金回收率;Ccap为初始投资成本;Cf为年均燃料成本;COM为年均设备运行维护成本;Cc为年均设备替换成本。

(1)年均资金回收率

年均资金回收率的计算公式为

式中:r为实际贷款利率;L为工程周期,一般边海防独立微电网系统工程周期为25年;i为5年以上名义贷款利率,目前为6.55%;f为通货膨胀率,目前为3%。

(2)初始投资成本

初始投资成本Ccap可表示为

Ccap=Nwdcpwd+NPVcpPV+NEScpES+Ndgcpdg

式中:cpwd、cpPV、cpES、cpdg分别表示单台风机、单个光伏单元、单个储能单元、单台柴油发电机的初始购买价格;Nwd、NPV、NES、Ndg分别表示风机、光伏单元、储能单元、柴油发电机的数量,它们是独立微电网规划问题中的决策变量,并且都为非负整数。

(3)年均设备替换成本

年均设备替换成本Cc可表示为

Cc=CcES+Ccwd+CcPV+Ccdg

式中:CcES、Ccwd、CcPV、Ccdg分别为储能系统、风机、光伏模组、柴油发电机的年均替换成本。

储能系统年均替换成本

CcES=kNESccES

式中:ccES为单个储能单元的替换费用;k为储能单元的损耗度指数,表示一段时间内消耗的储能单元占总量的比例。

(4)年均燃料成本

年均燃料成本Cf可表示为

Cf=cfwf

式中:cf为燃料单价;wf为燃料消耗量。

1.2 约束条件

(1)分布式电源最大装机容量约束

分布式电源最大装机容量约束如下所示:

式中:Nmax,wd、Nmax,PV、Nmax,ES、Nmax,dg分别表示微电网中实际场地等各方面条件限制下风机、光伏单元、储能单元、柴油发电机的最大安装数量。

(2)系统运行可靠性约束

在规划模型中主要运用系统累积供电不足量进行微电网可靠性评价,如下所示:

式中:ple为发电不足量占发电总量的比例;Ple(t)为系统在t时段内由于发电不足而切除的负荷功率;Ele为最大的累积供电不足量;Pld(t)为系统在t时段内负荷需求功率;T为总仿真时长(一般为1年);Δt为t时段的持续时间长度。

(3)可再生能源丢弃功率约束

可再生能源发电超过负荷需求且达到储能系统充电能力上限时,需弃掉多余电能。为尽可能提高可再生能源利用率,要求弃风光总量占理论发电总量的比例不得超过某一给定的上限值,如下所示:

式中:Pdp(t)为t时段内独立微电网系统丢弃的可再生能源功率;rre为给定的年弃风光上限值;Pre(t)为t时段内独立微电网系统可再生能源发电功率。

(4)污染物排放约束

以柴油为燃料的设备在运行过程中会向空气中排放二氧化碳、二氧化硫、一氧化碳、氮氧化合物等。因此,在微电网规划设计中要求污染物排放在一定范围之内,约束条件如下所示:

WCO2≥kCO2,dgfFdgf

式中:kCO2,dgf为柴油燃烧时二氧化碳排放系数;Fdgf为柴油消耗量;WCO2为系统最大二氧化碳排放总量。

2 系统能量管理模型

本文采用典型的储能循环充放电策略进行微电网运行控制。储能系统既可以充电也可以放电,它在整个系统中起着能量缓冲的作用。储能系统由多组储能单元聚合而成。在系统出现功率缺额而储能系统不能完全供电时,柴油发电机作为储能系统的能量补充和系统备用。

某一时刻t的系统状态为

ΔP(t)=Pwd(t)+PPV(t)-Pld(t)

式中:ΔP(t)为储能系统和柴油发电机都没有投入运行时系统的功率不平衡量;Pwd(t)、PPV(t)分别为t时段内系统风电输出功率、光伏输出功率。

整个系统的调度策略如下所示:

若ΔP(t)≥0,发电功率过剩,则储能系统充电。若充电功率或剩余电量均在储能系统的约束范围内,即ΔP(t)≤PESmax,c(t),则

PES,c(t)=ΔP(t)

式中:PES,c(t)为t时段内储能系统的充电功率。

PESmax,c(t)的表达式如下所示:

式中:PESmax,c(t)为储能系统额定充电功率;EESmax为储能系统最大可用容量;ES为储能系统漏电率;ηES,c为储能系统充电效率;EES(t)为储能系统在t时段内的能量水平。

当充电功率或剩余电量越限时,即ΔP(t)>PESmax,c(t),储能系统以最大允许功率PESmax,c(t)充电,其余部分通过备用负载或者其他方式消耗掉,从而出现能量浪费Pdp(t)。此时有

PES(t)=PESmax,c(t)

Pdp(t)=ΔP(t)-PES(t)

若ΔP(t)<0,发电功率不足,则功率缺额优先由储能系统放电来提供。若仅靠储能系统可以满足,即|ΔP(t)|≤PESmax,d(t),柴油发电机功率Pdg(t)为0,则

PES,d(t)=ΔP(t)

Pdg(t)=0

式中:PES,d(t)为t时段内储能系统的放电功率。

PESmax,d(t)的表达式如下所示:

式中:PESmax,d为储能系统额定放电功率;EESmin为储能系统最小可用容量;ηES,d为储能系统放电效率。

若储能系统放电功率或剩余电量越限,即Pdgmax+PESmax,d(t)≥|ΔP(t)|>PESmax,d(t),储能系统以最大允许功率PESmax,d(t)放电,其他部分由柴油发电机在其额定功率范围内补充,即:

PES(t)=PESmax,d(t)

Pdg(t)=|ΔP(t)|-PES(t)

如果储能系统和柴油发电机的功率补充仍然不能够满足功率缺额要求,即Pdgmax+PESmax,d(t)<|ΔP(t)|,这时系统就需要根据负荷的重要性切除非重要负荷,出现部分范围的停电。负荷功率不满足量为Psh(t),计算式如下所示:

Psh(t)=|ΔP(t)|-PES(t)-Pdgmax

式中:Pdgmax表示柴油发电机最大功率。

3 模型求解

对于本文的优化问题,可以采用差分进化算法进行求解,以Nwd、NPV、NES、Ndg为差分进化算法的基因,将目标函数作为适应度函数,最终寻找到一组最优的Nwd、NPV、NES、Ndg,使目标函数的值最小。整个算法流程如图1所示。

4 算例分析

为验证图1算法在求解远海岛礁微电网规划设计问题上的可行性与有效性,对一个较为简单的仅含电力子系统部分的风光柴储独立微电网的规划结果进行分析。该独立微电网系统的拓扑结构如图2所示。

该独立微电网系统的单个风机额定功率为20 kW,单套光伏模组额定功率为10 kW,单个柴油发电机额定功率为100 kW,单个储能系统额定容量为60 kW·h。为保证储能系统的安全性,提高储能系统寿命,设定其可用容量为50 kW·h,额定功率为50 kW。微电网规划设计年限为25年。具体参数见文献[6]。

系统负荷、10 kW光伏模组、20 kW风机的年历史数据如图3所示。由系统负荷历史数据可知,微电网中负荷需求存在较大的季节性变化,春夏季节负荷需求较高,秋冬季节用电需求较小。光伏的季节性不明显,这与该岛礁所处的低纬度有关,在该区域一年的日照时间都比较长,光伏资源较好。虽然风电输出的季节性没有系统负荷那么明显,但是也存在一定的季节性表现,春夏的风电资源优于秋冬的风电资源。

该独立微电网系统允许的最大年总缺电率为0.1%,最大年弃风光率为3%,可再生能源渗透率大于60%。风机、光伏模组、储能系统和柴油发电机的数量配置如表1所示。

图1 基于差分进化算法的独立微电网优化配置求解流程Fig.1 Solution procedure of isolated microgrid scheduling optimization based on differential evolution algorithm

图2 典型的独立微电网系统Fig.2 Schematic diagram of a typical isolated microgrid

表1风机、光伏模组、柴油发电机、储能系统可配置数量范围

Tab.1Configurationquantityrangeofwindturbine,PVmodule,dieselgeneratorandenergystoragesystem

项目最小配置量最大配置量储能系统180光伏模组5300风机5100柴油发电机250

差分进化算法种群规模为60,最大迭代次数为300,最大变异因子为1.5,最小变异因子为0.8,最大交叉因子为0.9,最小交叉因子为0.6。

运用差分进化算法求解典型风光柴储微电网系统规划模型,储能采用循环充放电策略,结果如表2所示。

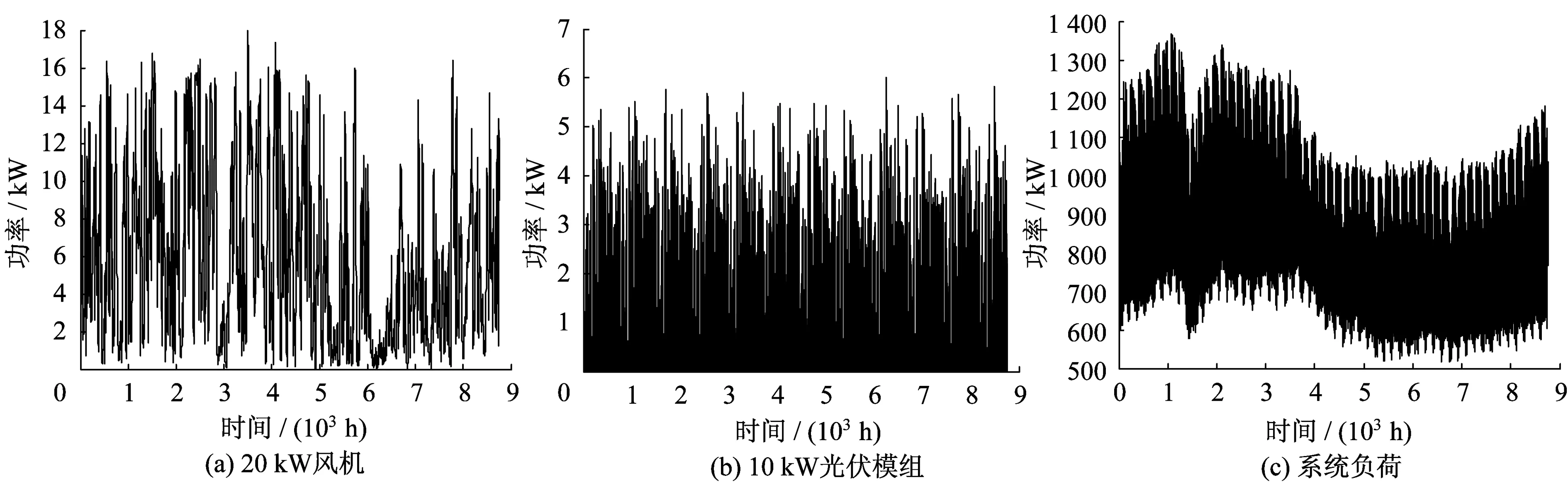
图3 历史数据Fig.3 Historical data

循环充放电策略中,储能系统吸收多余的可再生能源,超限的多余可再生能源被丢弃,因此一旦限制了可再生能源丢弃率则在某种程度上限制了储能系统配置。当可再生能源发电不足时,优先使用储能系统进行供电,只有在储能系统输出功率无法满足供电的情况下,才启动柴油发电机进行供电。因此,在循环充放电策略中柴油发电机实际上扮演着备用机组的角色。柴油发电机运行过程中会排放大量空气污染物,如二氧化碳、一氧化碳、碳氢化合物等,若考虑污染物排放成本,则会进一步增加柴油发电机的运行成本。

表2风机、光伏模组、柴油发电机、储能系统最优配置

Tab.2Schedulingoptimizationofwindturbine,PVmodule,dieselgeneratorandenergystoragesystem

项目数量储能系统56光伏模组142风机33柴油发电机11

如图4所示,系统最优年均投入成本为9.84×106元。储能系统充放电功率、柴油发电机运行功率、可再生能源丢弃功率及负荷供电不足功率如图5所示。

图4 年均投入成本Fig.4 Annual average capital cost

图5 最优配置情况下储能系统充放电功率、柴油发电机运行功率、可再生能源丢弃功率及负荷供电不足功率Fig.5 Charge/discharge power of energy storage system,diesel generator output,discarding rate of renewable energy resource and load demand shortage under optimal configuration

进一步分析可知,可再生能源丢弃率限值与系统运行成本之间的关系如图6所示。

由图6可知,总体趋势上,系统运行成本随着可再生能源丢弃率限值的上升而下降,但每一段下降趋势会有所不同。当可再生能源丢弃率从0到0.2%变化时,系统运行成本下降并不明显,但当可再生能源丢弃率从1.4%到1.6%变化时,系统运行成本下降非常明显。在某些丢弃率限值范围内,可再生能源丢弃率上升对系统运行成本并没有产生变化。

图6 可再生能源丢弃率限值与系统运行成本之间关系Fig.6 Relationship between discarding rate limit of renewable energy resource and system operation cost

5 结语

对于可再生能源丰富但传统电网供电困难的边海防地区用电问题,含多种分布式电源的独立微电网系统起着非常重要的作用。本文建立了含风光柴储的独立微电网系统的优化配置模型,并通过差分进化算法求解了该优化配置模型。最后,对系统运行成本与可再生能源丢弃率限值之间的关系进行了敏感度分析。本文研究为含多种分布式电源的独立微电网系统规划提供了一定参考。