基于RGBD信息和SFS融合的三维数字化方法

李 健, 李 丰, 何 斌, 刘富强

(1.陕西科技大学 电气与信息工程学院,陕西 西安 710021;2.同济大学 电子与信息工程学院,上海 201804)

随着三维(3D)技术的不断进步,越来越多的应用以3D的方式呈现给用户,因此3D技术的商业价值越来越凸显出来[1-3]。

真实物体3D展示方式相较于二维(2D)图像更为直观,而这种展示方式必须以一种操作简便、成本低、真实感强的3D建模技术为基础。“基于图像建模”技术为3D建模提供了关键支撑和必要条件。近年来,随着深度相机的广泛应用,用深度相机进行三维重建逐渐成为主流。

1 相关工作

随着消费级深度相机的普及,深度相机在稠密3D重建领域中的优势逐渐凸显出来,其对RGBD(red,green,blue and depth)多帧数据的融合取得了令人瞩目的成果[4-7]。然而,受限于Kinect等深度传感器获得的单帧深度图像的质量,重建结果存在平滑过度、细节不足等缺陷。

为了克服深度相机采集到的深度图像单帧精度不足的问题,Digne等[8]将深度数据分解为高频部分和低频部分,对低频部分进行融合并保持高频部分不变来提高重建精度。Haque等[9]提出了一种光度立体法和深度相机结合的重建技术,但是在对光源标定时假设反射率恒定,这就使得对于多反射率物体的重建结果不甚理想。文献[10]中采用了一种融合RGBD信息和彩色光度立体方法的非刚性物体3D数字化方法,但该方法也只适用于对纯色物体的3D重建。Berkiten等[11]在进行深度和法向量信息融合之前,先对由多个视角Kinect深度图计算得到的法向量进行加权求和。

本文提出了RGBD信息和明暗恢复形状(SFS)融合的数字化方法,并使用单个Kinect深度相机实现对多反射率物体的3D重建。首先对深度图进行双边滤波并估计其表面法向量,然后对SFS问题优化求解得到相应的光照模型参数,并考虑物体表面平滑约束,最后通过优化得到兼顾整体形状和细节信息的3D重建结果。

2 算法总体框架

本文算法总体框架如图1所示。

图1 RGBD信息和SFS融合的算法框架Fig.1 Algorithm framework of integration of RGBD information and SFS

首先,在室内自然光环境下使用Kinect深度相机获取被测物体表面RGBD信息;其次,对采集到的深度图进行双边滤波[11-12]处理,并估计双边滤波后深度图表面的法向量;然后,对SFS中的光照模型进行求解,即从表面法线和深度图的关系中求解出反射率,分别加以约束限制,从而优化整个光照模型;最后,构建一个全局代价函数来完成对目标物体深度值的优化求解,对该代价函数适当变形后,采用迭代优化方法求解出改进质量的物体表面3D数字化模型。

3 算法详细描述

3.1 深度图的预处理

对于采集到的深度图,首先通过深度阈值分割的方法提取出重建物体的有效区域,位于有效区域外的点云不参加计算以提高算法效率。选用点云处理领域常用的双边滤波进行平滑处理。

双边滤波方法是在高斯滤波方法的基础上改进后提出的。该方法将滤波权系数修改为高斯函数和图像灰度值的乘积,然后将修改后的权系数再与图像灰度值作卷积运算,这样在滤波的同时能够照顾到图像中的边缘数据,使图像在经过一般的高斯滤波后变得很模糊的边缘得以保持,而且边缘更加平滑。双边滤波方法数学表达式如下所示:

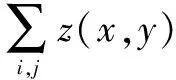
(1)

(2)

式中:σs为空间域标准差;σr为灰度域标准差。从式(1)、(2)中可以看出,ws随着像素点与中心点之间欧式距离的增加而减小,wr随着两像素灰度值之差的增大而减小。w由ws和wr的乘积组成,即w=wswr。

3.2 SFS问题中光照模型的求解

本文选取的光照模型为

L(i,j,n)=ρ(i,j)S(n)

式中:L(i,j,n)是光照强度;S(n)是阴影函数;ρ(i,j)是场景中某像素点的反射率;n是法向量。

在求解过程中,首先在朗伯体假设下求解S(n),然后用优化方法求解反射率ρ(i,j)。

朗伯体假设下求解S(n),求解的过程中设置ρ(i,j)=1,则

(3)

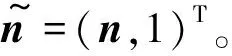
(4)

式(3)中,m是一阶球谐函数系数,可以通过彩色图像灰度值I使用最小二乘法优化求解出m,优化公式为

优化m后,可求出S(n),然后对反射率ρ进行求解。为了防止ρ过拟合,以相近区域内ρ变化不大为约束,构造先验约束项,如下所示:

式中:N是像素邻域,k是该邻域内的像素索引;ωck是灰度权重,ωdk是深度权重。ωck和ωdk计算式如下所示:

式中:σc为控制参数;σd为一个允许深度不连续的参数;zk为中心像素点坐标(i,j)邻域内像素索引k处对应的深度值;I(i,j)为中心像素点坐标(i,j)处的图像灰度值。最后,用正则化线性最小二乘法求解ρ,如下所示:

式中:λρ为先验项权重。

3.3 优化问题的构造与求解

3.3.1代价函数的构造

完整的光照模型已经得到,为恢复物体表面细节,构造出由SFS项、深度项和拉普拉斯平滑项三部分构成的代价函数,如下所示:

E(z)=λsEs(z)+λdEd(z)+λlEl(Δz)

式中:Es(z)是对应的SFS项;Ed(z)是对应的深度项;El(Δz)是对应的拉普拉斯平滑项;λs、λd、λl分别对应各自约束项的权重。对代价函数中的SFS项、深度项、拉普拉斯平滑项做进一步说明。

(1)SFS项

Es(z)

(5)

从式(4)物体表面法线和表面梯度的关系中得出,表面梯度可以由z的函数表示,然后用最小化灰度值和光照模型的差值即式(5)来求解z值。

(2)深度项

(6)

式中:z0是初始采集到的深度值;z是估计出的深度值。式(6)表示估计出的深度值与原始采集到的深度值的距离。

(3)拉普拉斯平滑项

该项的作用是将曲面上非常小的变化、噪声数据很快地扩散到它的邻域中,从而达到平滑的效果。本文为了保证在重建结果中保留更多的细节,所以设置该项权重参数较小。

3.3.2求解过程

从式(4)物体表面法线和表面梯度的关系可知,代价函数的SFS项是非线性部分,因此求解思路是首先求解线性部分,然后求解非线性部分。采用迭代方法,从一个初始值出发,不断更新当前优化变量,使代价函数下降,直到某个时刻代价函数值最小,此时算法收敛。

对法向量做如下变形:

对应的新的线性光照模型如下所示:

L(i,j,z)

对应的代价函数如下所示:

(7)

算法的输入包括z0、m、ρ(i,j)等光照模型参数,输出为zk,求解的步骤如图2所示。

4 实验结果分析

4.1 数据采集

实验时分别以单一反射率的石膏像和穿着多反射率服装的人为重建目标,在室内自然光环境下用Kinect深度相机进行数据采集。

图2 求解步骤Fig.2 Solving procedure

实验场景如图3所示,在距石膏像0.6～1.5 m的范围内进行拍摄。

图3 实验场景Fig.3 Experimental scene

生成的数据如图4所示。为了更方便展示,对深度图进行了加强对比度处理。

图4 彩色图和深度图Fig.4 Color image and depth image

4.2 3D数字化重建

通过比较,选择以下参数:σs=8,σr=15,σc=0.223,σd=7.12,λρ=0.1,λs=1,λd=0.4,λl=0.007 5。单一反射率石膏像的重建结果如图5所示,为了更好地展示重建结果,对面部细节进行放大。

为了比较本文方法与其他方法的重建精度,将使用Artec扫描仪扫描得到的三维模版与不同方法的重建结果进行注册配准,计算重建模型上点与标准模板间点的最近几何距离,并以伪彩色表示,如图6所示。

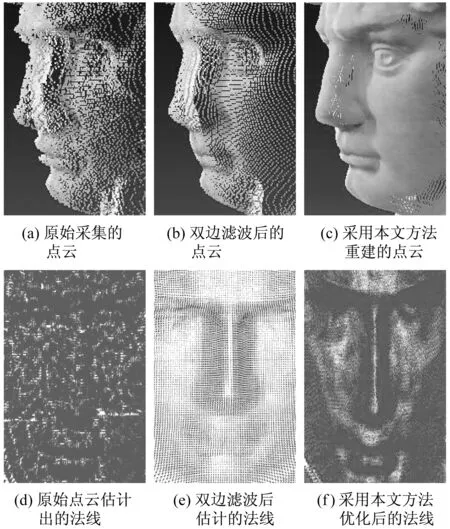
图5 石膏像重建结果Fig.5 Reconstruction results of plaster statue

三者误差比较如表1所示。从表1可以看出,采用本文方法所得结果误差更小。

图6 伪彩色图Fig.6 Pseudo color map

穿着多反射率服装的人的重建结果如图7所示。相较于利用改进的彩色光度立体方法实现的多色物体重建[10],本文没有光源、采样球等其他环境限制,实现方法更为简单。

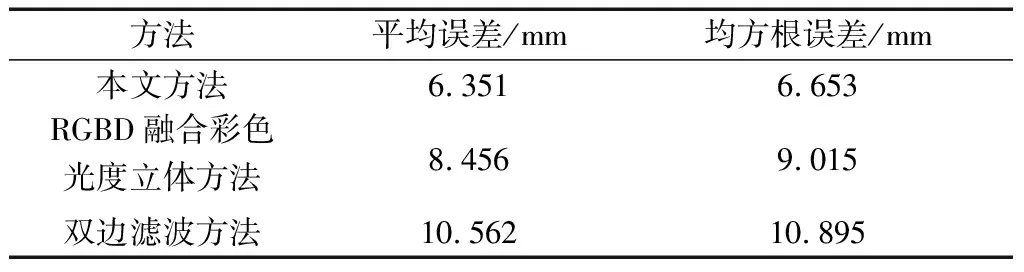
表1 误差比较Tab.1 Error comparison

图7 穿着多反射率服装的人的重建结果Fig.7 Reconstruction results of a person wearing multi-reflective clothes

5 结论及展望

本文采用RGBD信息和SFS融合的方法在室内自然光环境下进行实验,结果表明该方法较好地重建出了物体的细节信息,弥补了深度相机测量结果中噪声过大的缺陷。相较于RGBD融合彩色光度立体方法,本文方法解决了重建环境限制的问题,如不需要暗室环境、不需要光源、不限制物体反射率等。如何更好地实现全视角三维重建,是下一步的工作重点。