Cooperative spectrum sensing algorithm based on bilateral threshold selection against Byzantine attack

Zhu Hancheng Song Tiecheng Wu Jun Li Xi Hu Jing

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

Abstract：To deal with Byzantine attacks in 5G cognitive radio networks, a bilateral threshold selection-based algorithm is proposed in the spectrum sensing process. In each round, secondary uses (SUs) first submit the energy values and instantaneous detection signal-to-noise ratios (SNRs) to the fusion center (FC). According to detection SNRs, the FC conducts normalization calculations on the energy values. Then, the FC makes a sort operation for these normalized energy values and traverses all the possible mid-points between these sorted normalized energy values to maximize the classification accuracy of each SU. Finally, by introducing the recognition probability and misclassification probability, the distributions of the normalized energy values are analyzed and the bilateral threshold of classification accuracy is obtained via a target misclassification probability. Hence, the blacklist of malicious secondary users (MSUs) is obtained. Simulation results show that the proposed scheme outperforms the current mainstream schemes in correct sensing probability, false alarm probability and detection probability.

Key words：cognitive radio; Byzantine attack; bilateral threshold; misclassification probability; recognition probability

Recently, cognitive radio (CR) has been proposed to overcome the problem of limited available spectrum[1]. CR enables secondary users (SUs) to randomly access the spectrum. Due to the time-varying of the wireless channel, the signal-to-noise ratio (SNR) may become too low to obtain a reliable spectrum sensing. Hence, cooperative spectrum sensing (CSS) is proposed to deal with this issue[2]. In existing CSS, SUs need to send their local sensing information to the fusion center (FC), and then the FC makes a global decision[3]. However, this fusion scheme provides more opportunities for malicious secondary users (MSUs) to launch Byzantine attacks[4].

Nowadays, a series of solutions have been made to recognize MSUs. A reliable reference algorithm was proposed to reduce the influence of MSUs on spectrum sensing[5]. A trust node-assisted reference algorithm was put forward, in which the trust node was applied to screen out MSUs[6].

The traditional MSU detection scheme usually achieves a poor detection performance in a massive MSU and the low-SNR region. To enhance the performance in a relatively hash environment, a bilateral threshold detection scheme is put forward to resist Byzantine attacks.

1 System Model

1.1 Cooperative spectrum sensing

In this paper, an IEEE 802.22 wireless access network is considered, as shown in Fig.1. It consists of a CRN with one PU, one FC, andNSUs. Each SU performs the estimation of the energy value from the PU and sends it to the FC. Then, the FC decides the availability/unavailability of the PU. Therefore, each SU performs the energy detection for a time durationτ0. If we denote the sampling rate byfs, the energy value of SUiis given by

(1)

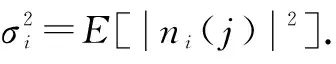
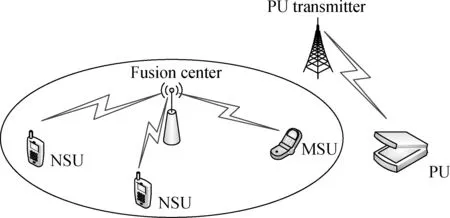
Fig.1 Wireless access network

(2)

whereγi=E[|hiS(j)|2] represents the SNR from PU to SUi. We assume that the FC has acquired the detection SNRγiand this can be realized by contacting the SUs[7].

1.2 Attack model

In order to efficiently carry out attacks,MSUs need to predict their own local decisions. By comparing the energy valueymwith a local thresholdφm, the local decision of MSUmcan be reached. A PU is considered available ifym>φm; otherwise, PU is considered unavailable.

After spectrum sensing, the individual sensing reportdmof each MSU is generated as

(3)

In this paper, the following Byzantine attack model is employed. Here, MSUs use their local decisions to perform attacks. It first makes a local decision. Then, it generates an abnormal Gaussian distribution value with the attack probabilityβm.

When the MSUmdoes not launch an attack, the energy value he/she submits isYm=ym. That is, he/she submits the energy value received in the energy detection phase. However, when the MSUmlaunches the attack, the Byzantine attack model is denoted as follows:

(4)

whereΛis a deviation resulting in a falsification of data.

2 Bilateral Threshold Selection Scheme

2.1 Data collection

The FC first picks up the energy values submitted by SUs in the history rounds. Hence, the FC can obtain the actual availability states of PU during the end of these history rounds[8](e.g. by interacting with the PU station). The energy values submitted by SUs and PU states are listed in Tab.1. After the pretreatment of energy values, the normalized energy values are shown in Tab.2.

Tab．1Collected energy values and PU states

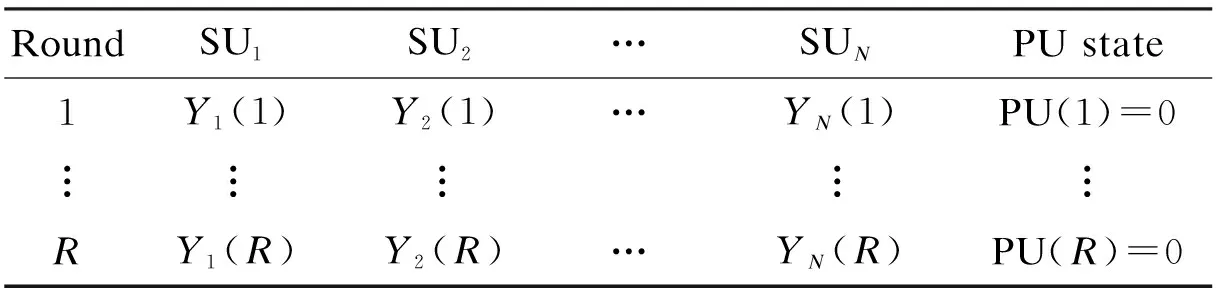
RoundSU1SU2…SUNPU state1Y1(1)Y2(1)…YN(1)PU(1)=0︙︙︙︙︙RY1(R)Y2(R)…YN(R)PU(R)=0

Tab．2Normalized energy values

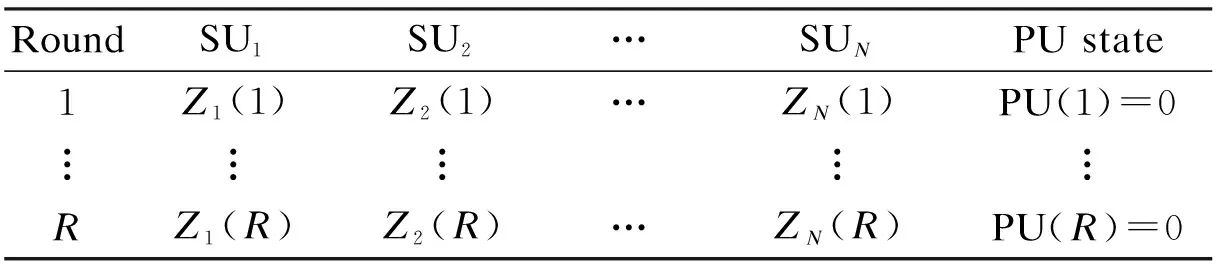
RoundSU1SU2…SUNPU state1Z1(1)Z2(1)…ZN(1)PU(1)=0︙︙︙︙︙RZ1(R)Z2(R)…ZN(R)PU(R)=0

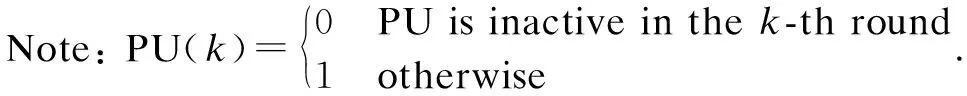
2.2 Pretreatment of energy values

The distributions of energy values submitted by SUimay change with the rounds. Therefore, formula (2) is revised as follows:

(5)

Drawing on the reference of standard normal distribution, the energy values are pretreated as

(6)

whereεis a positive data bias. Therefore, for NSUn

(7)

Formula (7) describes the distributions of the normalized energy values of NSUs. However, due to the existence of the attack rounds, the normalized distributions of MSUs under two hypotheses will generate additional changes. The variations of the normalized distributions between NSUs and MSUs will be identified by our bilateral threshold selection scheme.

2.3 Classification accuracy for normalized energy values

After treatment, Tab.2 can be obtained, and then the FC needs to analyze the normalized energy values inRrounds. The FC uses a rated value evaluation method to obtain the decision results of SUiinRrounds:

(8)

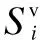
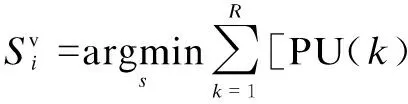
(9)

where ⊕ denotes exclusive-or logic. Therefore, the classification accuracy of SUiis

(10)

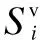
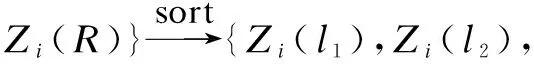
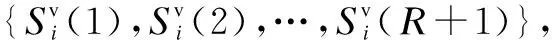
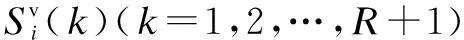
2.4 Bilateral threshold for normalized energy values

Here, two probabilities are introduced: recognition probability and misclassification probability. Recognition probability is the probability that MSUs are correctly recognized, while misclassification probability is the probability that a NSU is mistaken for a MSU.

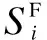
(11)

wherePi(z|H0) andPi(z|H1;ε) are the distributions underH0andH1in (7).P1andP0denote the probabilities that PU is present and absent, respectively. Solving the above gives

(12)

Hence, the theoretical classification probabilityp(ε) of SUiis

(13)

Then, a random variable is introduced:

(14)

(15)

Given the misclassification probabilityτ, the fluctuating rangeΔcan be calculated as

(16)

According to the central limit theorem, we can derive from the above expression that

(17)

Clearly, the recognition probability is a monotone decreasing function ofΔ. To maximize the recognition probability, we write formula (17) as an equation. Therefore,

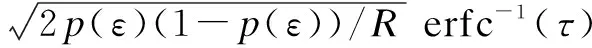
(18)

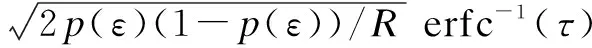
(19)

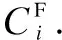
3 Description of the Bilateral Threshold Selection Scheme

In this part, the steps of the selection algorithm are introduced.

Step2For each SUi, the FC converts the energy valuesYi(k) intoZi(k) via (6).

Step3FC calculatesp(ε) and {uiL,uiH} by (17), (22) and (23).

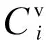
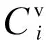
In order to demonstrate the effectiveness of the selection scheme, a simple likelihood ratio scheme is adopted to achieve the PU state as follows:

Step1Pick out the energy valuesYUj(k) of the SUs not included in the blacklist.

Step2Calculate likelihood ratio

Step3IfLr>1, then PU is available. Otherwise PU is unavailable.

As is shown from the scheme,P1andP0are counted by the actual state of the PU from Tab.2.PUj(y|Hv)(v=0,1) are the original distributions of the energy values in (5). {Uj}j=1,2,…,Mare the SU indices not belonging to the blacklist in the selection algorithm.

4 Simulation Results

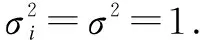
Fig.2 shows the MSUs screened out by our selection algorithm. Owing to the normalization of the energy values, SUs with different SNRs have the same bilateral thresholds. In Fig.2, a NSU is misclassified as a MSU

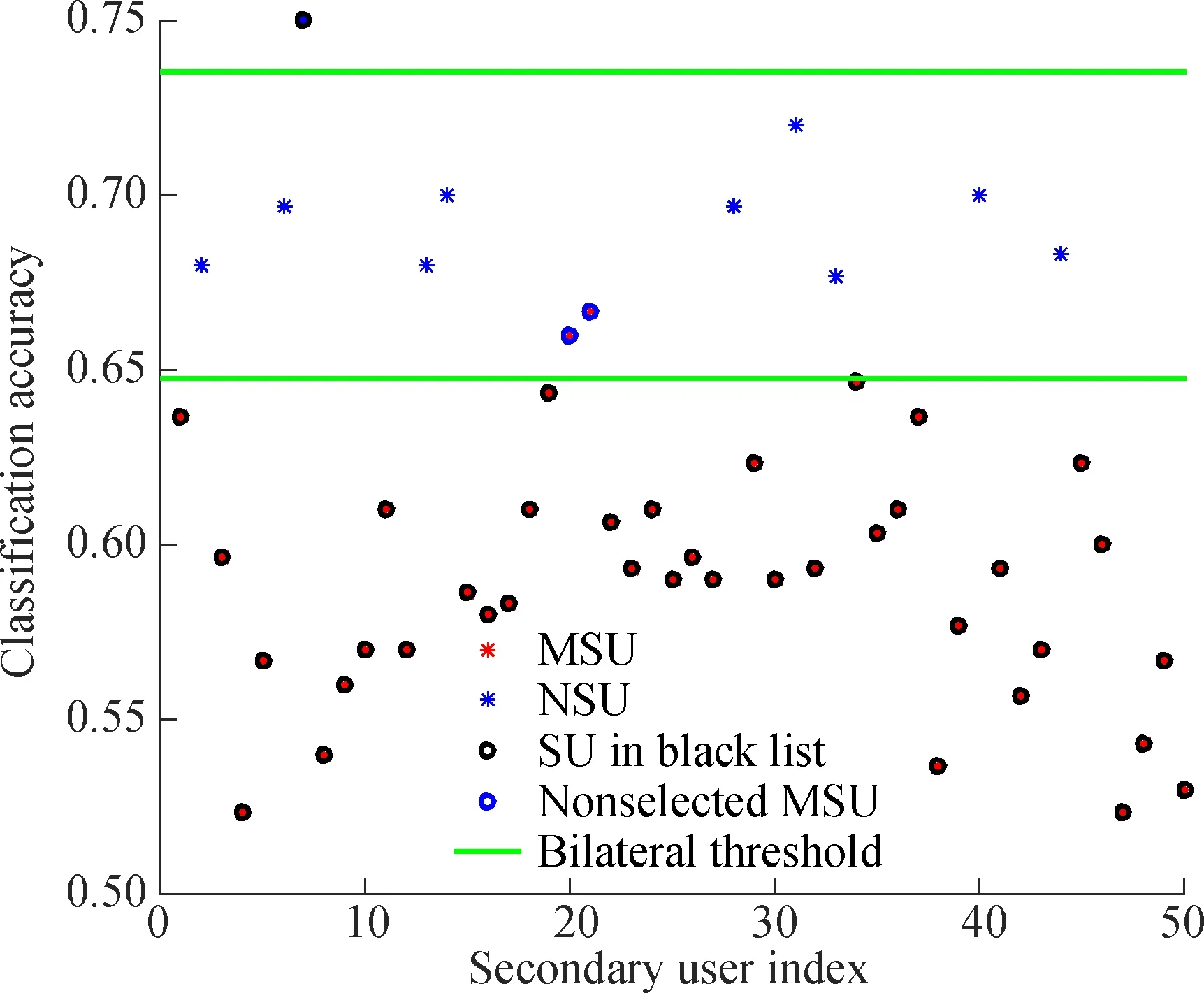
Fig.2 The filter result of MSUs in selection algorithm(βm∈[0.2，0.4])

(Its index is 7), and two MSUs are not screened out (Their indices are 20 and 21).

Fig.3 describes the correct sensing probabilities of our selection algorithm and the SVDD algorithm[9]with the rounds increasing. Due to the users’ mobility, the proportion of MSUs will change. The variations of the percentage of MSUs are marked with red circles. From Fig.3, our scheme achieves better performance than the SVDD algorithm. Besides, a largeRhas a positive impact on sensing performance, which is coincident with Eqs.(18) and (19).

Fig.3 The variation of correct sensing probability with rounds(βm∈[0.1，0.3])

Fig.4 shows the detection probability with the increase in the percentage of MSUs. In this figure, the traditional trust scheme[10]and the critical learning scheme[11]are the worst, while the sensing guard scheme[12]is better than them. This is due to the fact that the sensing guard scheme will impose severe punishments on the SUs who submit false sensing energy values frequently. However, our proposed scheme screens out most MSUs, which ensures excellent detection probability in scenarios with massive MSUs.

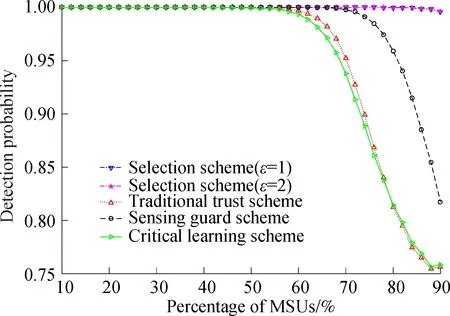
Fig.4 The variation of detection probability with percentage of MSUs(βm∈[0.2，0.4])

Fig.5 describes the impact of the percentage of MSUs on false alarm probability. We compare our selection scheme with the above algorithms. From Fig.5, we can see that the data biasεhas a modest impact on the sensing performance of the selection algorithm. Hence, the appropriate value of all data bias is allowed in our scheme.

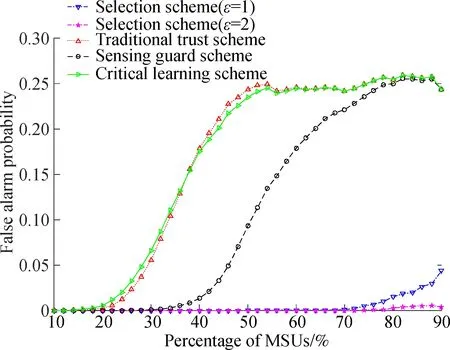
Fig.5 The variation of false alarm probability with percentage of MSUs(βm∈[0.2，0.4])

5 Conclusion

In this paper, we design a bilateral threshold selection scheme for MSU detection. Besides, we analyze the relationship between misclassification probability and the bilateral threshold. In simulation, we verify the performance of the algorithm in terms of a series of parameters. Hence, the proposed scheme can deal with the byzantine attacks in CSS to improve the robustness of the system.