Joint resource allocation scheme based on evolutionary game for mobile edge computing

Zhang Jing Xia Weiwei Huang Bonan Zou Qian Shen Lianfeng

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

Abstract：To satisfy mobile terminals’ (MTs) offloading requirements and reduce MTs’ cost, a joint cloud and wireless resource allocation scheme based on the evolutionary game (JRA-EG) is proposed for overlapping heterogeneous networks in mobile edge computing environments. MTs that have tasks offloading requirements in the same service area form a population. MTs in one population acquire different wireless and computation resources by selecting different service providers (SPs). An evolutionary game is formulated to model the SP selection and resource allocation of the MTs. The cost function of the game consists of energy consumption, time delay and monetary cost. The solutions of evolutionary equilibrium (EE) include the centralized algorithm based on replicator dynamics and the distributed algorithm based on Q-learning. Simulation results show that both algorithms can converge to the EE rapidly. The differences between them are the convergence speed and trajectory stability. Compared with the existing schemes, the JRA-EG scheme can save more energy and have a smaller time delay when the data size becomes larger. The proposed scheme can schedule the wireless and computation resources reasonably so that the offloading cost is reduced efficiently.

Key words：mobile edge computing; service provider selection; joint resource allocation; evolutionary game

Recently, mobile cloud computing (MCC) has been a great paradigm that combines wireless network service and cloud computing to enable mobile terminals (MTs) to take advantage of the abundant wireless resource and vast computation power ubiquitously[1-2]. With the emergence of more sophisticated applications, MTs expect to offload partial computing modules to be dealt with by the cloud service due to the limited battery power and smaller computing capabilities, which may impede the performance of service quality extremely[3]. However, the MCC introduces high latency since application data is sent to powerful servers which are distant from the MTs. Mobile edge computing (MEC) is widely regarded as a promising solution to address the problem. In terms of network topology, the computing or storage resources of the MEC are supposed to be in proximity of the MTs[4]. The MEC server is typically collocated with a base station in a network cell, and it is accessible to nearby MTs via a one-hop wireless connection[5]. In spite of its physical closeness to the MTs, the MEC server faces the drawback of limited computation resources.

The wireless networks are confronted with many challenges due to their limited radio and backhaul communications capabilities. The previous signal processing and transmission techniques applied in the conventional cellular networks may not be efficient enough to meet the above requirements[6]. The deployment of low-cost small cells is a very promising approach for efficient frequency reuse and spectrum sharing[7]. Small cells with a small coverage area and low transmission power usually include microcells, picocells, femtocells and relays. Heterogeneous networks (HetNets), which consist of numerous small cells and the traditional macro cells, meet MTs’ high-rate requirements. Therefore, in the scenario of offloading tasks to the MEC server, there is competition among numerous MTs over both constrained communication resources in HetNets and limited computation resources in the MEC[8].

In this paper, a joint cloud and wireless resource allocation scheme based on the evolutionary game (JRA-EG)is proposed for overlapping HetNets in mobile edge computing environments to satisfy MTs’ offloading requirements and reduce MTs’ cost. The main contributions of this paper are listed as follows. First, in the scenario of MEC, overlapping HetNets are considered. One base station and one MEC server configured on it constitute a service provider. Due to the differences in the capacity of wireless and cloud resources for different SPs, dynamic SP selection is included in this paper. Secondly, to measure the MTs’ cost for task offloading in MEC environments, the cost function is established, which consists of not only the energy consumption and time delay, but also the monetary cost. MTs with tasks offloading requirements in one service area form a population. In addition, different populations form a non-cooperative game. Thirdly, an evolutionary game is built to model the service provider selection and resource allocation of MTs. Centralized and distributed algorithms are used to obtain the EE of the JRA-EG game model, respectively. Simulation results indicate that both the centralized algorithm and distributed algorithm can reach the EE rapidly. The differences between them are the convergence speed and trajectory stability. Compared with the existing schemes, the JRA-EG scheme can save more energy and has less time delay when the data size becomes larger.

1 System Model

1.1 Network model

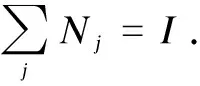
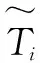
For base stations, the available spectrum bandwidth of BSkisWk. The bandwidth of each BS is averaged and allotted to all MTs connected to it. Considering the difference of BSs, the MTs are capable of acquiring different bandwidth by choosing different BSs. Moreover, the number of MTs connecting to BSkis denoted asnk.

Cloudlets can deal with tasks from all MTs connecting to them concurrently due to their multi-tasking capability. In order to get the utmost use of computation resources, cloudlets allocate all resources they have to the MTs according to a fair formula. Cloudlets of BSkare capable of handlingFkinstructions per unit time and tasks of MT are allocated toFk/nkinstructions.

Fig.1 Overlapping HetNets in mobile edge computing environment

1.2 Communication model

Orthogonal sub-channels are allocated to the MTs of macro and small cells. Therefore, there is no interference with each other. Specifically, the channel between each base station (BS) and its associated MTs experiences a fixed distance path-loss, a slow lognormal shadowing and Rayleigh fast fading. It is assumed that there is no power control and an adaptive multilevel quadrature amplitude modulation (M-QAM) is applied. Each BS assigns rate dynamically according to the received signal to noise ratio (SNR) per MT. Assuming the identical statistics over all frequency sub-channels and using adaptive modulation withLdiscrete rates, the long-term expected throughput (in bit/(s·Hz)) is expressed as[9]

(1)

wherel∈{1,2,...,L} and [Γl,Γl+1) denotes the interval of SNR.

It is assumed that both SBSs and MBS schedule their MTs in a round robin (RR)[10]. In this situation, all the MTs subscribed to the same SP share the long-term expected throughput equally which is straightforward for the RR scheduling algorithm.ηkdenotes the throughput for BSk. Hence, the expected throughputRkfor the MT subscribing to BSkcan be calculated asRk=(Wkηk)/nk.

1.3 Computation model

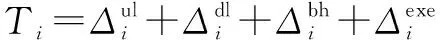
(2)

(3)

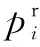
The monetary cost of MTiconsists of two parts. The first part is the communication cost and the second part is the computation cost.qkandgkare the price per unit transmission rate and the charge per unit computation resources of SPk, respectively.

Ci(fi,wi)=qkwiηk+gkfi

(4)

According to Eqs.(2) to (4), the overhead of the mobile edge computing approach in terms of time delay, energy consumption and monetary cost can be computed as

(5)

The MTs in the same service area cooperate with each other and different service areas compete for the cloud and wireless resources of SPs. The object function of joint cloud and wireless resource allocation is

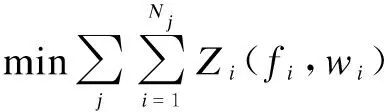
(6)

The objective of Eq.(6) is to minimize all MTs’ overhead in the HetNets under the latency constraints.

2 Evolutionary Game Formulation

The joint cloud and wireless resource allocation problem is modeled by taking advantage of a dynamic evolutionary game. Solution refinement and bounded rationality as well as dynamics are the remarkable characteristics of the evolutionary game[12]. Solution refinement ensures the existence and uniqueness of EE. Bounded rationality refers to the fact that players can slowly change their strategies to achieve the EE solution, which is specifically adjusted to the time-varying performance satisfaction. Due to the fact that the communication and computation capacity of each SP is limited, MTs at the different service areas, which are geographically separated, compete to share the available bandwidth and CPU cycles. Here, an evolutionary game is used since it can capture the dynamics of SP selection (i.e., strategy adaptation) based on the available information of the MTs.

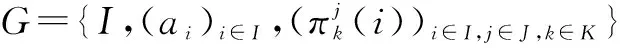
● Players For a particular service area as shown in Fig.1, each MT in each service area which can choose multiple SPs including MSP and SSPs, is a player of the game. Note that the MTs which can connect only to one SP are not involved in the game.

●Population The population in this evolutionary game refers to the set of MTs in the same service area. The number of populations isJ.

●Strategy The strategy of each MT refers to the selection of SP. Accordingly, the SP selection strategy set can be denoted asK={0,1,2,...,K} which refers to the selection of the MSP andKSSPs.sj, which denotes the SP selection strategy set of populationj, is the subset ofK. The MTiin populationjselects SP strategyaifromsj.Sis aJ×(K+1) SP selection state matrix of all populations. MatrixSis composed of elements 0 and 1, whereS[j,k]=0 shows that SPkcannot be connected andS[j,k]=1 shows that SPkis accessible.

●Cost function The cost is the expected consumption of a player choosing a certain SP selection strategy. The cost of a player is determined by energy consumption, delay cost and monetary cost.

To obtain the cost, the cost function is used to quantify MTs’ consumption on tasks offloading. For a particular populationj, the cost of a MT choosing SPkcan be expressed as

(7)

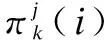
(8)

The cost, communication resource allocation and computation resource allocation depend on all MTs’ SP selection strategies in terms of the population state as well as the strategies of the SPs.

The definition of EE is as follows.

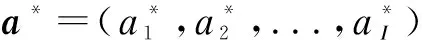
The population state spaceX*can be derived bya*. Therefore, the population state spaceX*is regarded as EE.

3 Centralized Algorithm for JRA-EG

In this section, the centralized algorithm based on replicator dynamics is introduced.

3.1 Centralized algorithm formulation

In the dynamic evolutionary game, an individual from a population, who is able to replicate itself by the process of mutation and selection, is called a replicator[12]. In this case, a replicator with a lower cost can reproduce itself faster. The replicator process can be modeled by using a series of ordinary differential equations, which is called replicator dynamics. The proposed centralized algorithm based on replicator dynamics provides a method to acquire the population information of others and converges towards an equilibrium selection. The centralized algorithm is also efficient to investigate the speed of convergence of strategy adaptation required to reach a stable solution in the game[10].

We consider an evolutionary game of SP selection in a heterogeneous wireless network where the population of MTs in areajcan choose the available MSP and SSPs. The speed of the MT in observing and adapting the SP selection is controlled by gain parameterσ,σ>0. In the game model, the aim of each MT is to minimize its cost. Hence, we can formalize the replicator dynamics as

(9)

(10)

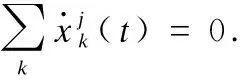
3.2 Centralized algorithm design

In the initial phase, all MTs randomly choose one SP from the SP selection strategy sets and the centralized controller computes the initialized population state matrix. Then, each SP allocates communication and computation resources on average according to the number of MTs connected to it. Next, MTs compute individual offloading cost and send it to the centralized controller. The centralized controller computes the average offloading cost of every population. There is a double circulation in the cycle phrase. The algorithm is executed iteratively and each episode consists of population state matrix updating, resource assignment updating, offloading cost updating and information exchanging. Finally, EE is derived when the MTs in each population have the identical offloading cost.

Algorithm1Centralized algorithm

Input:I,K,J,Nj, cycle indexland error factorζ.

Output: The population state space of EEX*.

for alli=1 toIdo

MTiin populationjrandomly choose SPkfromsj.

end for

The controller computes the population state vectorxj.

Each SP acquiresnkand allocateswkandfkon average.

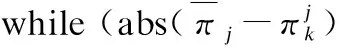
for allj=1 toJdo

for all populations.

Each SP acquiresnkand allocateswkandfkon average

end for

end while

Evolutionary equilibriumX*is derived.

4 Distributed Algorithm for JRA-EG

When a centralized controller is unavailable, each MT has to evolve its SP selection decision gradually and independently. The reinforcement learning approach can reach the target by analyzing the surrounding environment. In this case, a Q-learning algorithm[13-14], which is a type of reinforcement learning, is applied to the solve the JRA-EG problem.

4.1 Distributed algorithm formulation

In this section, a distributed algorithm for JRA-EG based on Q-learning is formulated. In the distributed algorithm, complete cost information of other MTs in the same or different populations is no longer required for SP selection due to the learning ability. The distributed algorithm acquires the EE of the evolutionary game by Q-value.

For the distributed algorithm,ai∈sjis the current selection strategy state of MTiin populationj.uiis the control state for MTiin populationjwhich is the subsequent selection strategy of MTi.

The subsequent state ofaiis denoted as

(11)

The distributed algorithm acquires the EE of the evolutionary game by the Q-value. The Q-value is used to maintain the knowledge of MTs about each SP, and the decision can be made by MTibased on the Q-value. In Section 2, we have assumed that the MTs in populationjare requested to offload the identical task load and have the same requirement for the impact factor in a task offloading. Therefore, the Q-value of MTs in the same populationjselecting the same SPkis identical. The MTs in populationjshare the Q-value vectorQ[j,k],k∈K. Therefore, the dimension of Q-value isJ×(K+1) since there areJpopulations andK+1 SPs. If populationjcannot connect to SPk,Q[j,k] is identically equal to zero. The distributed algorithm starts withQ0=[0]J×(K+1).

For iteration timest=0,1,2,,..., the distributed algorithm updates the iterativeQ-value using the learning rateλtby

(12)

wheretis the iteration times of the Q-value;λis the learning rate, 0≤λt<1; andθis the discount factor, 0<θ≤1;Qjis the 1×(K+1) row vector; andπj(al,ul) denotes the cost vector of populationj.πj(al,ul) can be derived by

(13)

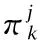
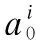
(14)

All populations update the iterative Q-value by

Qt+1(al,ul)= (1-λt)Qt(al,ul)+

(15)

whereQandπ(al,ul) areJ×(K+1) matrices.

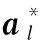
(16)

The convergence property of the distributed algorithm is associated with learning rateλt. OnceQ*converges, the EE of JAR-EG is obtained. Theorem 1 describes the convergence condition.

Theorem1Fort=1,2,..., letQt(al,ul) be updated by Eq.(15). Ifλt,t=1,2,..., satisfies

(17)

andθsatisfies 0<θ≤1, then the iterative Q-valueQt(al,ul) converges to its optimal value ast→, that is

ProofThe proof is similar to that in Ref.[13].

4.2 Distributed algorithm design

In the distributed algorithm, all MTs need to compare the current Q-value with other strategies’ Q-values and adjust their selection strategy by themselves.

The initialization is similar to the centralized algorithm.Different from the centralized algorithm, the algorithm imports Q-learning rate, discount factor, learning possibility and Q-value. In the cycle phrase, there are three circulations. In each episode, the resource allocation, SP selection strategy, offloading cost and Q-value are updated. Unlike the centralized algorithm, every individual needs to utilize the Q-value to learn the change of the entire network. The algorithm does not stop until the Q-value matrix of each MT is identical.

Algorithm2Distributed algorithm

Input:I,λ,θ, error factorζ.

Output: Population state space of EEX*.

for alli=1 toIdo

MTiin populationjrandomly chooses SPkfromsj.

end for

Each SP acquiresnkand allocateswkandfkon average.

Computesπ(al,ul) by Eq.(13) andQby Eq.(15).

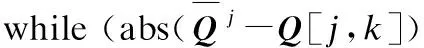
for allj=1 toJdo

for alli=1 toNjdo

rand=rand() is a random number between 0 and 1.

if (rand≤ρ)

MTirandomly chooses SPkfromsj.

else

end if

Each SP acquiresnkand allocateswkandfkaveragely for MTs.

Computesπ(al,ul) by Eq.(13) andQby Eq.(15).

end for

end for

end while

Evolutionary equilibriumX*is derived.

5 Performance Analysis and Evaluation

5.1 Parameter settings

The simulation scenario is described in Fig.1. We regard HetNets with one MSP and four SSPs,K=4. So, the SP strategy set isK={0,1,2,3,4}. We set the number of populationJ=2Kand the number of MTs in populationjis randomly distributed between 0 and 100. The bandwidth and processing ability of SPs are respectively set to beW=[200,80,80,80,80] Hz andF=[80, 40, 40,40, 40] 109cycles. The throughput of BSs is set to beη=[1.5,2,2,2,2] bit/(s·Hz) and the transmission power of MTs isp=[10,5,5,5,5] mW. The price for communication resources is [0.5, 0.1, 0.1, 0.1, 0.1] dollar/MHz. The charge for computation resource is 0.1 dollar/(106cycles). For the distributed algorithm, the discount factor is set to beθ=0.98[13]and the learning possibilityρ=0.1[12].

5.2 Performance evaluation of JRA-EG scheme

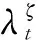
In Fig.4, the population evolution algorithm, centralized algorithm and distributed algorithm are compared. In Refs.[12,15-16], a population evolution algorithm is used to achieve the EE. The population evolution algorithm not only relies on the centralized controller to collect population cost information, but also depends on each MT when comparing individual cost with the average cost of the population it belongs to. From Fig.4, we can conclude that the convergence speed of the centralized algorithm is the fastest and that of the distributed algorithm is the slowest. Besides, the curve of the centralized algorithm approach is smooth and steady while the other two algorithms fluctuate with the increase in iteration times until reaching equilibrium. The population evolution algorithm and the distributed algorithm change the population state individually so that the changing speed is inconsistent among the loop episodes. Compared with the population evolution algorithm, the centralized algorithm has a faster equilibrium speed while the distributed algorithm has no requirement for population information exchange. To sum up, both the centralized and distributed algorithms can reach EE rapidly and have their respective advantages.

Fig.2 Equilibrium time with different gain parameters in the centralized algorithm

(a)(b)

(c)(d)

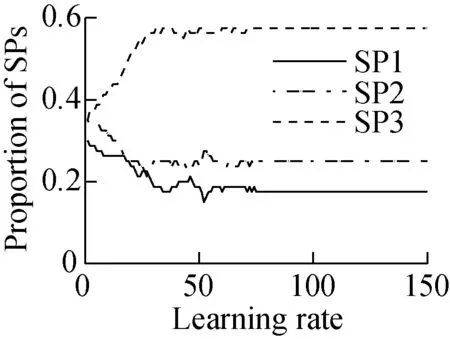
Fig.3The effect of the learning rate in the distributed algorithm.
(a)λ=0.7; (b)λ=1-1/(t+1); (c)λ=0.5(sin(t+1)+1); (d)λ=0.5(cos(t+1)+1)

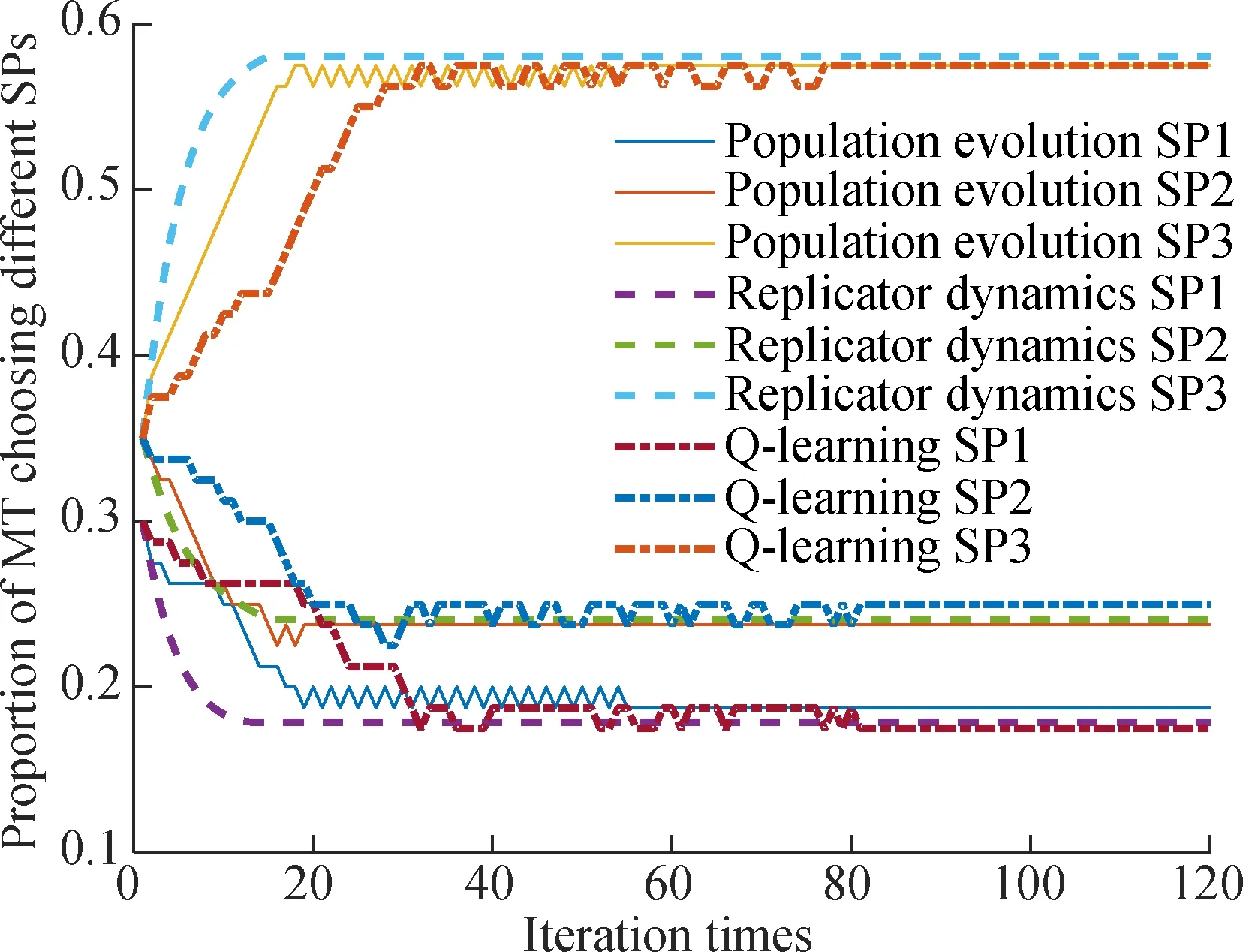
Fig.4 Algorithm comparison among population evolution, centralized algorithm and distributed algorithm

From Fig.5, we can observe that the increasing tendency of EE, ES and proposed JAR-EG schemes of energy consumption differ from each other. The increasing speed of the EE scheme is the fastest while that of the proposed scheme is the slowest. At the beginning, the ES scheme consumes the least energy and the proposed scheme consumes the most energy. However, the energy consumption of the proposed scheme becomes less with the input data size increasing. When the input data size is larger than 8 Mbit, the energy consumption of the proposed scheme is the lowest. The delay consumption comparison among the EE, ES and proposed JAR-EG schemes is described in Fig.6. We can clearly observe that the proposed scheme has the least time delay compared with the other schemes. By analyzing the energy consumption and time delay of the EE, ES and proposed JAR-EG schemes, we can conclude that the proposed JRA-EG scheme has better performance and effectiveness when input data size becomes larger.

Fig.5 Energy consumption comparison

Fig.6 Time delay comparison

6 Conclusion

In this paper, we solve the problem of joint communication and computation resource allocation based on the evolutionary game (JRA-EG) in mobile edge computing environments. To the best of our knowledge, the work is the first one of integrating the SP selection with resource allocation so as to achieve the minimum joint mobile terminals’ energy consumption, time delay and monetary cost. An evolutionary game is established to select SPs and allocate cloud and wireless resources dynamically. We take advantage of the centralized algorithm based on replicator dynamics and the distributed algorithm based on Q-learning to obtain the EE of the JRA-EG game model, respectively. Simulation results verified the effectiveness of the centralized algorithm and distributed algorithm.