中考数学(北京卷)评价改革之函数

王亮亮

(北京教育考试院 100083)

1 引言

从2012年开始，北京市中考数学函数类试题从题型结构、考查内容、设问方式等方面进行了改革与创新，引起了广大师生的关注.一方面，试题在函数的基本概念、基础知识和数形结合思想等方面对学生的要求很高；另一方面，试题的背景新颖、内涵丰富、思想深刻，能很好地对考生进行区分；再一方面，试题对初中的函数教学起到了正导向作用.但通过调研、听课发现，由于对试题的了解不够全面，很多教师在讲解时遇到了一些问题，如“函数基本活动经验”试题，把侧重点放在了几何上，忽略了函数的本质及其工具性.本文以2018年中考数学(北京卷)函数类试题为例，对试题进行一次理论性和实践性的总结，与大家分享试题背后的思想和试题对教学的导向作用，希望能给一线教学提供一定的参考.

2 评价改革基础

准确把握《义务教育数学课程标准(2011年版)》对函数部分提出的本质性要求是改革实施的必要前提，也是了解试题对一线教学具有正导向作用的基础.

2.1 联系与变化是函数的本质特征

在初中阶段，虽然没有系统介绍映射、函数三要素、函数性质(如单调性，奇偶性)等理论知识，但结合具体的函数，需要有效地渗透、逐步地揭示函数的本质特征——联系和变化，以及基本数学思想和方法(变化与对应的思想、数形结合的思想).函数的本质特征须贯穿于函数教学的始终，并且是评价改革的理论基石.

2.2 正确理解函数的概念是函数学习的基础

函数是从数量的角度反映变化规律和对应关系的数学模型，也就是说变化与对应的思想是学习函数的基本思想.正确理解函数概念，须结合变化与对应的思想，通过对丰富的实例进行归纳和抽象，在这一过程中把握好函数的实质(两个变量的相互联系，对于自变量确定的每一个值，对应的函数值都唯一确定).函数的本质就是两个变量之间的一种对应关系，表示函数的方法，最常用的是解析式法、列表法、图象法三种.需要注意的是在函数学习的过程中，不要形式化的引入函数定义，定义讲解的形式化会引起函数理解的形式化，只是记住了具体的表达形式，而没有理解函数的本质.

2.3 解决实际问题是函数学习的主要目标

函数是研究运动与变化的数学模型，与实际联系十分紧密，它来源于实际又服务于实际，从实际中抽象出函数有关概念，又运用函数解决实际问题，这是函数学习的主要目标.

2.4 函数的图象与性质是函数学习的主体

通过对函数的图象与性质的研究，从数量和图形两个方面及相互联系中，可以发现函数本质特征是联系与变化，这是函数学习的主线.反过来说明，图象与性质是函数学习的主体.

2.5 数形结合思想是研究每类函数的基本思路和方法

平面直角坐标系把数与图形有机地结合起来，有利于用代数方法研究几何问题，也有利于借助图形直观地探索数量关系的规律性.在初中阶段，对函数的研究是初步的，但研究过程已体现出从函数的数量特征以及图象的几何特征来刻画每类函数的性质，这说明数形结合思想是研究每类函数的基本思路和方法.

2.6 正确的学习函数的经验是函数思维形成并利用其解决实际问题的必要前提

简单地说，函数思维就是利用联系与变化的观点，理清对应关系及其规律，并能解决问题的思维.函数思维的形成离不开正确的学习函数的经验的积累.从具有实际背景的问题入手，采用列表或列解析式的方法，对其数量关系进行抽象和梳理；从中认识常量和变量的主要特征，并概括出变量间关系的共同特征；由此理解函数、自变量和函数值等概念；在重新认知具有类似实际背景实例的基础上，重现函数及相关概念的本质特征，形成函数的一般概念；通过函数概念的学习，领会函数图象是具有直观反映和描述函数变化规律的工具；全面、系统地理解函数的三种表示形式(列表、解析式和图象)，进一步形成对函数意义的认知；利用数形结合思想这一基本思路和方法研究每类函数.

3 评价改革实践

在“评价改革基础”中，已经系统地介绍了函数体系，它既是学习函数的理论基础，也是评价改革的依据，它们是一脉相承的.

例1下图是老北京城一些地点的分布示意图.在图中，分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系，有如下四个结论：

①当表示天安门的点的坐标为(0，0)，表示广安门的点的坐标为(-6，-3)时，表示左安门的点的坐标为(5，-6)；

②当表示天安门的点的坐标为(0，0)，表示广安门的点的坐标为(-12，-6)时，表示左安门的点的坐标为(10，-12)；

③当表示天安门的点的坐标为(1，1)，表示广安门的点的坐标为(-11，-5)时，表示左安门的点的坐标为(11，-11)；

④当表示天安门的点的坐标为(1.5，1.5)，表示广安门的点的坐标为(-16.5，-7.5)时，表示左安门的点的坐标为(16.5，-16.5).

上述结论中，所有正确结论的序号是

(A)①②③(B)②③④(C)①④(D)①②③④

解析在平面直角坐标系中，坐标的表示可以是多样的，坐标的核心是对应关系而不是具体表示形式，具体可以表现为根据实际问题的背景，选择合适的坐标原点和单位长度，建立平面直角坐标系，方便实际问题的解决.

本题考查的落脚点是对应关系，以老北京城一些地点的分布为背景，以正东、正北方向为x轴、y轴正方向建立平面直角坐标系，利用给出的天安门和广安门的坐标，判断左安门的坐标.在建立平面直角坐标系的过程中，无论以哪个位置为坐标原点，从位置关系来说，天安门、广安门和左安门两两之间的绝对位置不变，从数量关系来说，天安门、广安门和左安门两两之间的相对距离也是不变的.绝对位置和相对距离是“对应关系”，它们是不变的.通过对①②③④分析，不难发现，②是在①的基础上改变了单位长度，③是在②的基础上改变了坐标原点，④是在③的基础上改变了单位长度，但“对应关系”是不变的.

对于平面直角坐标系的理解，既要抓住其核心是对应关系，又要抓住其数形结合的“性质”.利用平面直角坐标系，可以把数与图形有机地结合起来，有利于用代数方法研究几何问题，也有利于借助图形直观地探索数量关系的规律性.将数形结合思想作为研究每类函数的基本思路和方法，可以更深入地理解函数概念及其表达形式，积累正确地学习函数的经验，有利于函数思维的培养.

小腾根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究.

下面是小腾的探究过程，请补充完整:

(1)按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；

x/cm0123456y1/cm5.624.673.762.653.184.37y2/cm5.625.595.535.425.194.734.11

(2)在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x，y1)，(x，y2)，并画出函数y1，y2的图象；

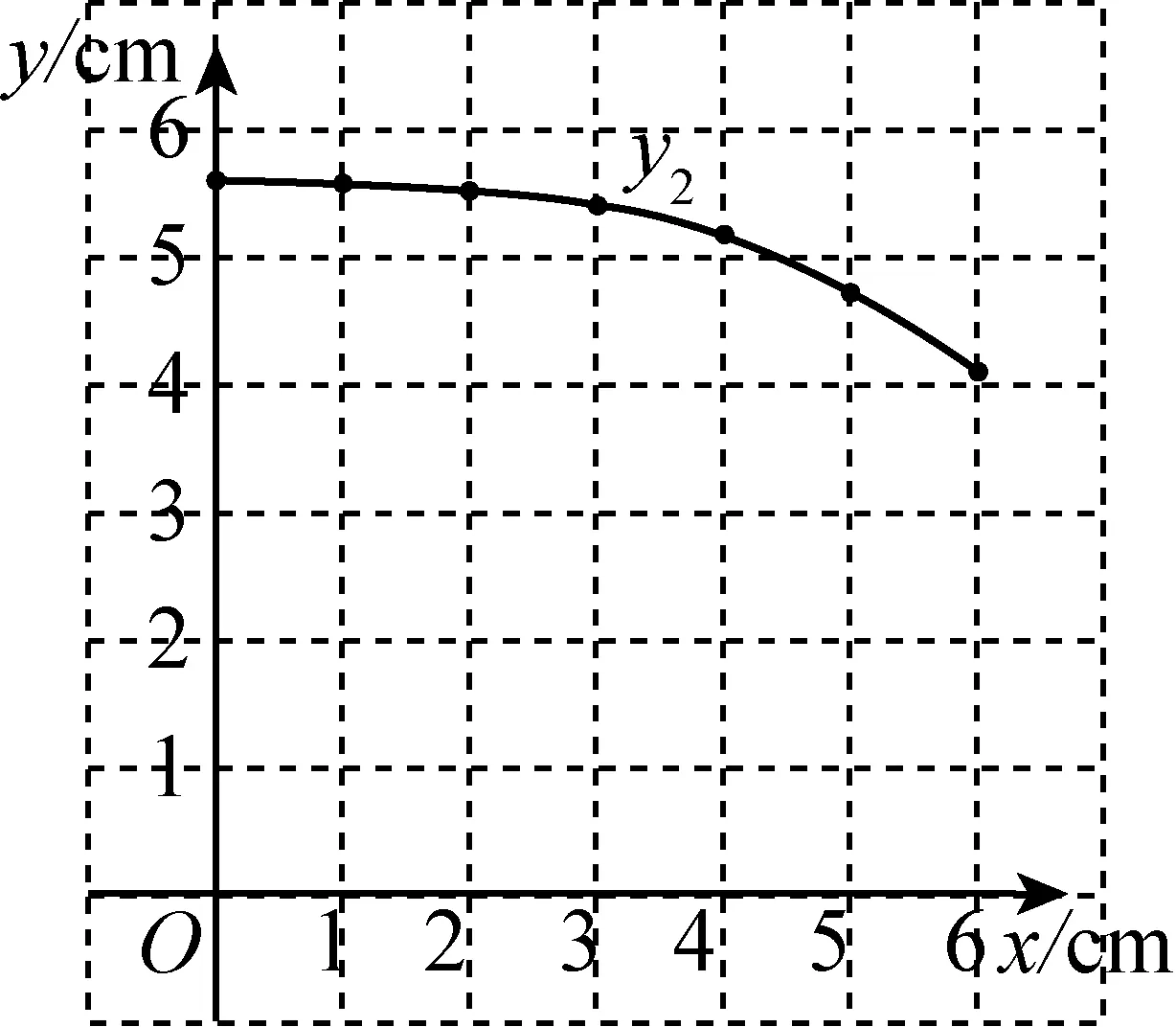
(3)结合函数图象，解决问题：当△APC为等腰三角形时，AP的长度约为cm.

解析本题考查的落脚点是利用函数的思维解决问题，以P是弦AB上一动点，弦PC，AC随着点P的变化而变化为背景，运用联系与变化的观点，厘清量与量之间的关系，发现对应关系及其规律，重现研究函数的内容与方法，在经历取点、画图、测量、列表、建系、描点、画函数图象的过程中，探究变量之间的关系，研究函数的图象与性质，利用函数思维及有关知识解决问题.上述过程，从表面上看是再现函数学习过程，考查函数学习过程中积累的经验，但从本质上看是能否用函数思维看待、思考、分析并解决问题.

当点P从点A向点B运动时，弦PC和AC的长度都随着点P的变化而变化，在这一过程中体现了变化与对应的特征.通过取点、画图、测量、列表，可找到AP与PC之间、AP与AC之间都是一种对应关系，将待解决的几何问题抽象成为了函数模型，利用函数思维解决几何问题.通过建系、描点、画函数图象，利用数形结合的思想，把问题“当△APC为等腰三角形时，AP的长度约为cm”转化为对函数y1，y2的图象进行研究.当PA=PC(或AP=AC)时，反映出因变量y1(或y2)等于自变量x，在函数图象上反映出函数y1(或y2)的图象与直线y=x的交点就是弦PA等于弦PC(或弦AP等于弦AC)；同样地，当CA=CP时，反映出函数值y1=y2，在函数图象上反映出函数y1的图象与函数y2的图象的交点就是弦CA等于弦CP.上述过程体现了几何问题抽象为函数问题，利用函数的思维使问题得以解决的方法.

题目的设置方式体现了考试改革对教学改革的引导作用，引导教学关注函数的本质特征，关注函数的概念，关注函数的刻画性质，关注函数学习的主体，关注函数学习的基本思想与方法，避免形式化的概念引入，机械化的画图象，让函数真正地从实际中来，又真正地回到实际中去.

例3在平面直角坐标系xOy中，直线y= 4x+ 4与x轴、y轴分别交于点A，B，抛物线y=ax2+x- 3a经过点A，将点B向右平移5个单位长度，得到点C.

(1)求点C的坐标；

(2)求抛物线的对称轴；

(3)若抛物线与线段BC恰有一个公共点，结合函数图象，求a的取值范围.

解析函数的图象与性质是函数学习的主体，数形结合思想是研究函数的基本思路和方法.在研究函数图象过程中，需要借助数形结合的思想发现归纳和总结函数的性质；研究函数性质过程中，需要借助数形结合的思想直观感受数量关系的规律性.

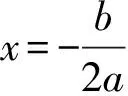
抛物线y=ax2+x- 3a的对称轴为x= 1，经过点A(-1，0)，利用轴对称性可知，抛物线经过点(3，0).抛物线开口方向不确定，须对其进行分类讨论；抛物线顶点纵坐标不确定，须确定开口方向后，对其进行分析；抛物线与线段BC恰有一个公共点，须结合开口方向的分类讨论，分析抛物线顶点的位置，利用数形结合思想，通过画图分析，确定满足条件的边界，带点计算，确定a的取值范围，如图所示.

关于a的取值范围确定的过程，体现出从函数的数量特征以及图象的几何特征来刻画每类函数的特征，说明数形结合思想是研究每类函数的基本思路和方法.

4 结束语

本文从《义务教育数学课程标准(2011年版)》函数内容本质性要求的角度切入，从函数的本质特征，函数学习的基础，函数学习的主要目标，函数学习的主体，研究每类函数的基本思路和方法，函数思维形成的前提等方面阐述了函数知识体系，通过分析试题，阐述理论与实践如何相结合，进行深入思考，既是对落实课程标准理念和精神的总结，更是提出了教学改革和考试改革共同努力的方向和目标.北京中考数学学科的改革还在不断地进行探索与完善之中，文章若有不妥之处，请批评指正.