一道考研数学试题的多种解法

崔静静，赵思林

（内江师范学院数学与信息科学学院 641112）

发散思维是创造性思维的最主要的特点，是测定创造力的主要标志之一。一题多解能够培养学生的发散思维能力，引导学生深入地探索问题，培养学生灵活多变处理问题的能力[1]。本文介绍2018年全国硕士研究生入学考试一道数学试题的6种解法，作为一题多解的一个实例，仅供参考。原题如下：

方法1（教育部考试中心参考答案）

评析：方法1属于常规方法，可用凑微分法（第一类换元积分法），将原式变为，然后考虑用分部积分。用观察法可得，从而将裂项，变为是考查考生的一个分水岭，此处看似简单，对学生的思维要求极高。

方法2

方法3

令t=ex-1，则x=ln(t+1)，所以所以原式

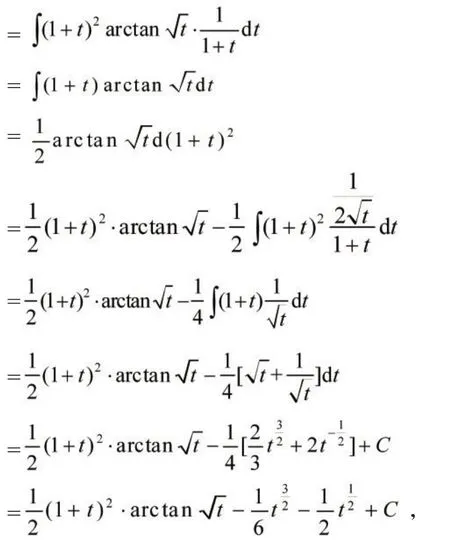
由t=ex-1，则上式

方法4

方法5

方法6

将t=ex代入此式，

评析：相比方法1和方法2，方法3至方法6均用换元法，把原式变为熟悉的形式，将复杂的计算和推证简化。

以上解法表明：凑微分法是求不定积分最简单的方法之一[2]。在解积分题目时，应注意一题多解，用多种方法解同一道题通常比盲目的做几道题的效果好。选择一道好的例题，通过一题多解，一题多讲，可以巩固学生的知识，训练其思维，开拓其视野[3]。