带限QMBOC信号的加权匹配接收技术

刘 亮，马忠强

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081；2.河北科技大学 信息科学与工程学院，河北 石家庄 050018)

0 引言

随着全球卫星导航系统(GNSS)的逐渐完善，新体制信号也得到了一定的发展。信号调制方式的设计关系到基带信号接收层面的解调、捕获和跟踪，因此信号设计上的缺陷往往会影响到信号的锁定状态和电文的准确度。由于越来越多的信号在同频点被发布，为了使不同的信号可以更好地共享有限的频谱资源，GPS和Galileo在现代化的信号中采用了新的调制方式MBOC，位于1 575.42 MHz频点，其中，GPS L1C采用TMBOC(6，1，4/33)，Galileo L1则采用CBOC(6，1)[1]。在北斗信号的设计中既要考虑与同一频点其他信号满足兼容性要求，保证信号之间的互操作能力，又要支持多种模式的接收处理，例如低端接收机只接收低阶BOC信号，高端接收机组合接收高阶和低阶BOC[2]。除此之外，还要考虑到知识产权保护，避免国外专利的封锁。为了打破国外专利技术对我国的封锁，我国科研人员提出了正交复用二进制偏移载波(Quadrature Multiplexed Binary Offset Carrier，QMBOC)调制方式，这种调制方式将高阶BOC与低阶BOC调制到正交2个分量上，降低二者之间互相关影响，而且满足了不同用户的接收需求，同时打破了国外的专利封锁[3]。

然而，QMBOC在实际场景下，往往会受到滤波器宽度的影响，在带限场景下与无线带宽的性能上存在差异，在实际接收机接收时需要考虑到滤波器的影响[4]，本文针对带限情景下的QMBOC调制方式进行仿真，分析不同滤波器带宽下，信号测距偏差曲线(如SCB曲线、Scurve Bias曲线)的性能，提出新的功率加权匹配的接收解调算法。

1 QMBOC调制

QMBOC属于MBOC(Multiplexed BOC)调制方式的一种，由欧盟和美国最先提出，一般的MBOC调制信号可以写为：

φBOC(m，n，γ)=(1-γ)φBOC(n，n)+γφBOC(m，n)。

(1)

MBOC是按照一定配比完成低阶BOC(n，n)和高阶BOC(m，n)的组合，从而完成二者的复用，对于MBOC的复用方式并没有固定的要求，信号设计者可以根据实际需要调整2种BOC信号的能量和复用关系[5]。GPS使用的TMBOC调制是利用2种BOC在时域上的组合完成复用，而Galileo则是利用正相MBOC和反向MBOC组合的方式[6]，可以写为：

(2)

为了打破国外知识产权对我国的封锁，我国的信号设计者提出了QMBOC调制方式，利用2种BOC在频域上进行区分，二者的相位角相差90°，可以写为：

(3)

以BOC(1，1)和BOC(6，1)组合的QMBOC为例，其功率谱如图1所示，在频谱中心区域为BOC(1，1)，在两侧为BOC(6，1)，这样的频谱结构能够充分利用频段资源[7]。

与之对应的相关解调的本地码信号为信号本身的共轭，这样可以保证高阶BOC的能量与低阶BOC能量相叠加，QMBOC信号的自相关为：

图1 QMBOC信号功率谱

(1-γ)RBOC(n，n)(τ)+γRBOC(m，n)(τ)。

(4)

这样完成数据的相关可以消去2种BOC之间互相关的影响，使得信号的能量能够被充分利用。在实际接收时，采用匹配接收的方式将高阶和低阶的BOC分量的能量有效组合，从而完成信号的接收[8]。QMBOC匹配接收方式如图2所示。

从现有研究资料来看，关于旅游休闲小镇资本运营相关问题的研究资料较多，也获取到一定成果，但还应该开展更为深入的研究，以下将从四个方面对现有资料应该继续探究的问题进行阐述：

图2 QMBOC匹配接收方式

其中，加权相加的公式为：

(5)

(6)

式中，Rc(τ)为高阶BOC和低阶BOC的互相关结果，在I支路上，其结果为2种BOC自相关能量的叠加，为了保证叠加相关峰最高，按照各自相关峰高度进行加权，充分利用2种信号的能量[9]。

2 带限QMBOC性能分析

上述分析是在无限带宽的前提下进行的分析，以BOC(6，1，4/33)为例，在无限带宽时，信号的相关峰如图3所示，理想信号此时严格满足BOC(1，1)与BOC(6，1)功率比为29∶4，此时信号相关峰两侧完全单调下降，只是在平台处下降幅度较缓。

然而，在带限情况下，以±8 MHz的砖墙滤波器为例，信号的相关峰如图3所示，此时相关峰两侧受滤波器影响，造成两侧不再单调下降，而且对于BOC(1，1)与BOC(6，1)功率比也不再满足29∶4的关系，根据不同带宽可以仿真得到对应不同滤波器带宽下的BOC(1，1)与BOC(6，1)功率比比值[10]，如图4所示。

图3 QMBOC调制信号相关峰

图4 不同滤波器带宽2种BOC信号功率比值

出现这种情况的原因是因为在滤波器滤波后，滤波带宽外的部分能量被滤波器滤掉导致的，而这部分能量也作为2种信号能量的重要组成部分[11]。由图4可知，信号带宽越窄，BOC(6，1)所占能量比重越少，原因是BOC(6，1)分量在带外存在很多能量，如图5所示。

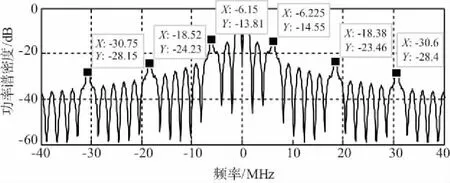
图5 BOC(6，1)能量峰值点分布图

BOC(6，1)每隔6×1.023 MHz存在一个能量峰值点，而在±8 MHz的滤波器带宽下，很多能量峰值点被滤掉，这也间接解释了为什么不同带宽下功率比值呈现阶梯式下降，即每当一个能量峰值点被滤掉，二者的功率比值产生剧烈变化[12]。而对于BOC(1，1)信号，主要能量集中于±5 MHz带宽内，所以滤波器对它能量造成的损失较小，通过仿真可以得到不同滤波器带宽下，2种信号能量损失情况，如图6所示，BOC(1，1)最大的损失不超过3%，而BOC(6，1)在滤波器较窄(小于±15 MHz)时，能量会损失30%左右。

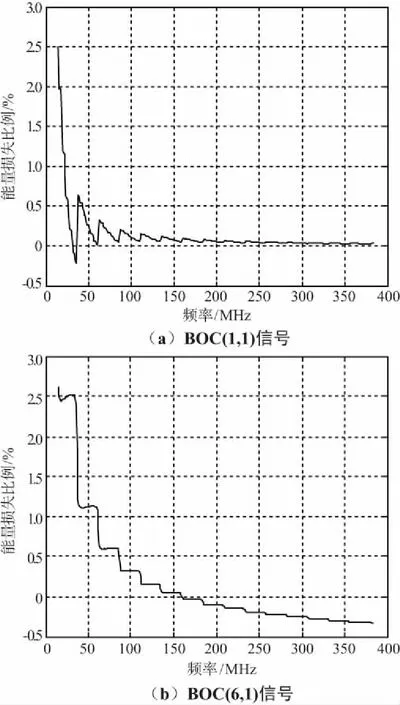
图6 不同滤波器带宽下BOC信号能量损失情况

滤波所滤掉的高频分量还会使得相关峰尖锋的形状发生变化，从而导致QMBOC滤波后的相关峰在平台处出现凹陷，这样的凹陷也会使得实际接收间隔在平台处附近的接收机在跟踪的过程中出现失锁[13]。

3 带限QMBOC多路复用接收

由于QMBOC信号在滤波后体现出的一些特殊情况，除了在相关间隔的选取上需要注意避开平台凹陷处，其次就是自适应匹配当前带限信号的2种信号功率配比，进行合理的加权，以获得最大的相关能量输出[14]。

对于滤波后的信号，假定其幅频和相频特性较好，不会在滤波器层面造成不同频率能量和相位关系的剧烈变化，设滤波后的信号表达式为[15]：

(7)

(8)

二者的自相关为：

(9)

由于相位并未出现旋转，正交2个分量之间的互相关值远小于自相关值，因此，忽略式(9)的互相关，匹配接收的自相关可以写为：

(10)

为了求得相关峰能量最大值，令相关峰最大值为目标函数F(β)，可以写为：

(11)

求导可得：

(12)

令F′(β)=0，可得到在β=γ′时取得最小值，所以在滤波后采用与滤波后的功率比做加权匹配求和可以得到更大的相关输出。

4 仿真结果分析

根据上面的推导结果，在QMBOC滤波带宽确定的前提下，分别利用2种BOC信号的本地码求得接收处理得到的带限信号中2种信号的功率比值，并按照新的功率比值重新加权，利用本地处理的低通滤波器进行整形，将整形后的输出作为新的本地码[16]，功率加权匹配流程图如图7所示。

图7 功率加权匹配法流程

使用当前信号内2种BOC信号功率比值作为加权系数可以得到最大的相关输出，使用原功率比的联合相关峰与使用新方法进行功率加权匹配的相关峰比较图如图8所示[17]。

图8 功率加权匹配相关峰与原功率比匹配相关峰对比

从图8中可以看到，加权后的相关峰能量高于原有方法的能量，而且能量提升至原来的1.1倍左右，具备更强的抗噪声能力，而且在平台处也比原来的单调性改善很多[18]，对2种情况相关峰的SCB曲线进行分析，得到的结果如图9所示。加权后的信号SCB曲线偏差较小，证明相关峰两侧的对称性较好，在接收机锁定时不容易出现失锁的情况，可以提升导航定位服务性能[19]。

图9 功率加权匹配SCB与原功率比匹配SCB对比

5 结束语

通过对QMBOC信号滤波后的性能进行分析，指出了带限的QMBOC信号存在缺陷，并通过推导得出了利用带限信号的功率配比重新生成本地码的加权功率配比法，与先前的原功率配比法相比，存在一定优势，提升了相关输出值，在QMBOC相关峰平台处更加平坦单调，降低了接收机跟踪失锁的可能性。