未来5 a华北地区小麦生育期降水量变化趋势分析

房坤宝 ，崔克俭 ，孙青芳 ，王曙光 ，史雨刚 ，孙黛珍

（1.山西农业大学农学院，山西太谷030801；2.山西农业大学文理学院，山西太谷030801；3.山西农业大学工学院，山西太谷030801）

政府间气候变化专门委员会（Intergovernmental Panel on Climate Change，IPCC）气候变化 2014 年综合报告指出，气候变化会减少亚热带地区可再生的地表水和地下水资源，会加剧行业间对水的争夺；在典型浓度路径（RCP）8.5情景下，许多中纬度地区和亚热带干燥地区，平均降水可能会减少，极端降水事件很可能强度更大、频率更高。华北地区地处北半球中纬度亚热带季风气候区，降水年际变化波动大，空间分布极不均匀，为干旱多发区[1-3]。研究表明，过去60 a华北地区粮食因干旱损失量不断增加[4]。冬小麦是华北地区主要粮食作物[5]，小麦生长发育时期恰好是缺水季节——冬春季[6]。近年来，影响冬小麦生产的冬春季降水量的减少越来越成为制约小麦生产的主要因素，引起政府与社会各界的高度关注[7]。

20世纪70年代后期，气候变暖背景下，全球降水量受东亚季风影响逐渐减弱[8]，我国降水年际变化地域差异明显，西北、东北、长江流域及华南等地降水呈明显增加趋势[9-10]，但我国的西北东部、东北大部和华北地区冬小麦主要生育期降雨明显减少，其中，西北东部和华北地区的夏季降水减少趋势明显[11]，以华北为中心的冬麦区冬春季的降水总体呈减少趋势，加剧了水资源和农业发展的矛盾并严重威胁到冬小麦的安全生产和粮食增产[12]。

本研究利用多年趋势线、3 a滑动平均值法、Hurst指数法、M-K突变分析等降水量变化特征分析方法，分析未来华北地区北部冬麦区降水量的变化趋势。并在此基础上，基于加权马尔可夫链预测方法分析降水量与时间的关系[13]，构建该地区降水量预测模型，预测未来降水量，并验证降水变化趋势的准确性，从而为华北地区冬小麦生产应对未来气候变化、制定科学管理措施提供依据。

1 材料和方法

1.1 数据来源

选取华北地区北京、天津、太原、石家庄4个站点的气象数据来进行研究。数据来源于中国气象数据网（http://data.cma.cn/）4个站点近60a的气象资料。

1.2 研究方法

1.2.1 趋势分析 通过曲线的趋势线性方程斜率的正负来判断变化趋势，并利用其相关系数R2对其进行检验。首先，对降水量数据进行处理，得到降水序列，列出散点图。然后对数据进行滑动平均，得到新序列。最后，从散点图中得出趋势线，并计算趋势线方程。

1.2.2 Hurst指数分析 Hurst指数可以判断时间序列的持续性。当H＝0.5时，表明时间序列可以用随机游走来描述；当0.5＜H＜1时，表明时间序列存在长期记忆性，即将来的趋势与过去一致，H越接近1，持续性越强。当0≤H＜0.5时，表明时间序列具有反持续性，即将来的趋势与过去相反，H越接近0，反持续性越强。本研究采用最常见的R/S（RescaledRangeAnalysis）分析方法计算Hurst指数。

1.2.3 M-K突变分析法 M-K突变分析法是通过分析UFK和UBK曲线图，检测降水序列的变化趋势，明确降水突变的年份。若UFK或UBK的值大于0，则表明序列呈上升趋势，小于0则呈下降趋势。当曲线超过临界直线时，表明该时间区域上升或下降趋势显著。若UFK和UBK这2条曲线出现交叉点，且交叉点在临界线之间，则交点对应的时刻便是突变开始时间。

1.2.4 加权马尔可夫链降水预测模型 加权马尔可夫链预测模型是国内具有代表性的降水预测方法，是时间和状态都离散的马尔可夫过程。

预测模型建立如下。

第一，各站点降水序列利用滑动平均法得到新的降水序列。

第二，对新序列进行状态分配，根据分级标准确定各时段滑动平均降水量的状态。利用样本均方差对降水量进行分级，通常按枯水年、偏枯水年、平水年、偏丰水年、丰水年划分为5个等级，分别为。其中，为降水平均值，s为标准差。a1在［1.0，1.5］之间取值，a2在［0.3，0.6］之间取值。本研究中a1取1.0，a2取0.5。

第三，通过状态分配得到各阶到各状态的转移矩阵。对第二步所得到的结果进行统计，得到不同滞时（步长1～5）的一步转移概率矩阵。其中，转移概率Pij是描述其演化进程最重要的量。

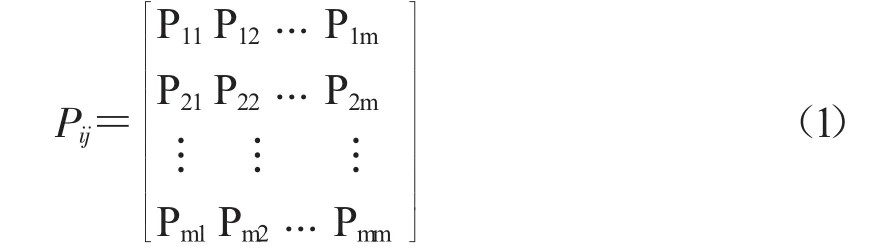
式中，Pij为降水量处于状态i时，下一情况变为状态j的概率。

第四，确定新序列各阶自相关系数，并且对自相关系数进行加权分析，得到各阶自相关的权重。其中，各阶自相关系数计算公式如下。

其中，rk表示第k阶（滞时步长为k）自相关系数，xt表示第 t年的年降水量，xt＋k表示第 t＋k 年的年降水量，表示降水量序列的多年平均值，n为年降水量序列的长度。

根据公式（2）确定各滞时权重系数pk，其计算公式如下。

其中，m为按预测需要计算得到的最大阶数。

第五，分别以前年各时段的汛期降水量作为初始状态，结合相应的各阶转移概率矩阵，可预测出降水量的状态概率。

第六，对同一状态的各预测概率Pi加权求和，得降水量处于该状态的预测概率。

max{Pi，i∈E}所在的状态即是这个预测时段降水量的预测状态，查询步骤（2）即可得到降水量的预测范围。将预测值加入到原序列中，重复以上步骤可进行下一年的降水量状态的预测。

第七，预测结果计算与验证。对各状态分别赋予相应的权重，权重集 d＝ ｛d1，d2，d3，d4，d5｝，其中，η为最大概率作用，通常取2或者4，本研究取2；再计算模糊集理论中的级别特征值，H＝Σmii×di，式中，m＝5，i为状态，di为权重。

确定最大概率的状态后，根据公式（5）确定系统在预报时段的预报值。

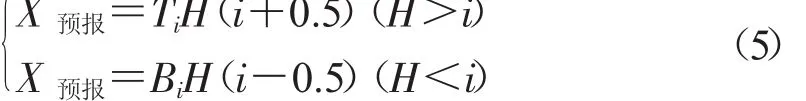
其中，Ti，Bi分别是状态区间值的上限与下限。

最后利用前几年的预测值与实际值比较，由于中长期水文预报的复杂性，一般认为相对误差小于20%即可。预测误差若满足预测精度需要，则加权马尔可夫链模型进行降水量中长期预报有效可行。

2 结果与分析

2.1 降水量变化趋势分析

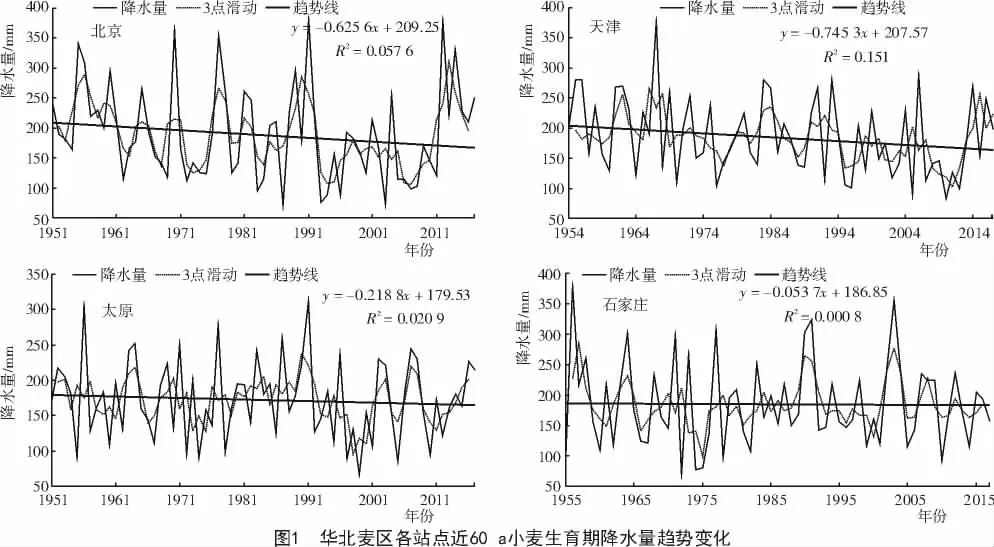
由图1可知，华北地区小麦生育期降水趋势曲线和3 a滑动平均值曲线基本上都呈下降趋势，下降幅度0.53～7.45 mm/10 a。各站点降水量平均值下降趋势为4.12 mm/10 a。下降趋势幅度从高到低排序为：天津＞北京＞太原＞石家庄。同时从3 a滑动平均值曲线可以看出，每个地区降水量有较强的波动性和规律性。其中，每个地区趋势线的相关系数R2的绝对值都远小于1，也就说明降水量近年波动较大，下降趋势不明显。同时也说明用趋势线代表降水量变化意义并不大，只能用来判断变化趋势。

2.2 突变分析

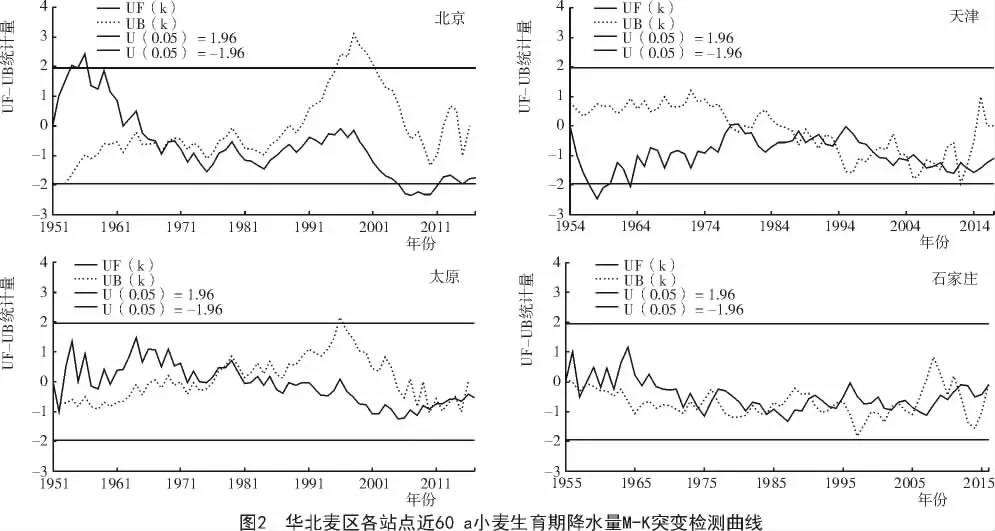
由图2可知，北京地区自1962年以来，UF值一直小于0，降水量呈下降趋势；在2006—2013年小于下临界值，其下降趋势十分显著。据UF和UB曲线交叉点的位置，可知北京降水量下降是一个很明显的突变，具体时间从1967年开始。天津地区自1978—1979年UF值在0附近波动，其他年份均小于0，降水量呈下降趋势，但不显著。太原地区从1984年至今，UF值小于0但都未超过临界点，处于降水量下降趋势，但不显著；在1953—1983年，UF值大于0，降水量处于上升状态，确定太原年降水量从20世纪80年代开始下降是一个突变现象，具体时间由交叉点可知从1981年开始。另外，几个交叉点周围都没有降水趋势的变动，所以，不是突变点。石家庄地区自1967年至今UF值一直小于0，且均未超过临界值，故降水量一直呈下降状态。总体来看，降水突变年份可能出现在20世纪七八十年代， 但近年来各地区生育期降水量基本均呈下降趋势。

2.3 Hurst指数分析

对北方冬麦区各站点的降水量进行R/S分析，得到各站点冬小麦生育期降水量Hurst指数（表1）。结果表明，降水量在各个站点的Hurst指数值均大于0.5且都接近0.5，表明在华北地区冬小麦生育期的降水量将持续下降，但其持续性不强。

表1 华北地区冬小麦生育期降水量的Hurst指数值

2.4 加权马尔可夫链降水预测模型

为了对未来降水量有个更明确的了解，对各站点近60 a降水量使用马尔可夫链进行模拟。利用已知年份降水量验证降水模型的准确性，最后得出预测年份的降水量。以太原地区为例，过程为：基于各站点降水序列利用滑动平均法得到新的降水序列（表2）；对新序列进行状态分配，根据分级标准确定各时段滑动平均降水量的状态（表3）；根据公式（1）通过状态分配得到各阶到各状态的转移矩阵；确定新序列各阶自相关系数，并且对自相关系数进行加权分析（由公式（2）计算得到各阶自相关系数，k1＝0.332，k2＝0.108，k3＝0.333，k4＝0.171，k5＝0.054）；根据状态转移矩阵与权重系数计算加权求和值（表5）。

利用降水序列中的状态，计算近60 a的滑动平均降水量的各种步长的状态转移概率矩阵如下。

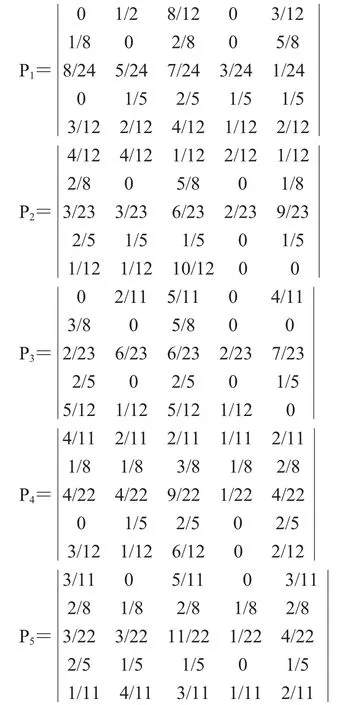
由公式（3），（4）计算得到表 4。由表 4 可知，当i＝5时，P5＝0.412，为最大值，说明 2014年的滑动平均降水量状态为5，即数值区间为［228.5，＋∞）。

由公式（5）求出2013年滑动平均降水量为282.38 mm，而实测值为340.40 mm，相对误差为17.04%。

同理，重复以上方法可得各站点其他时段的滑动平均降水量预测验证（表5）。

从表5可以看出，2013—2017年这5 a的马尔可夫链预测值与真实值误差都在50 mm上下，预测状态基本上相同，与实际情况基本吻合。从数值上讲，太原、北京、天津的预测相对误差都较小，都不超过20%。

由于中长期水文预报的复杂性，一般认为相对误差小于20%即可。预测误差满足预测精度需要，证明加权马尔可夫链模型进行降水量中长期预报是有效可行的。因此，加权马尔可夫链模型可以进行下一步预测。

重复上述方法，可得各站点未来5 a的预测降水量（表 6）。

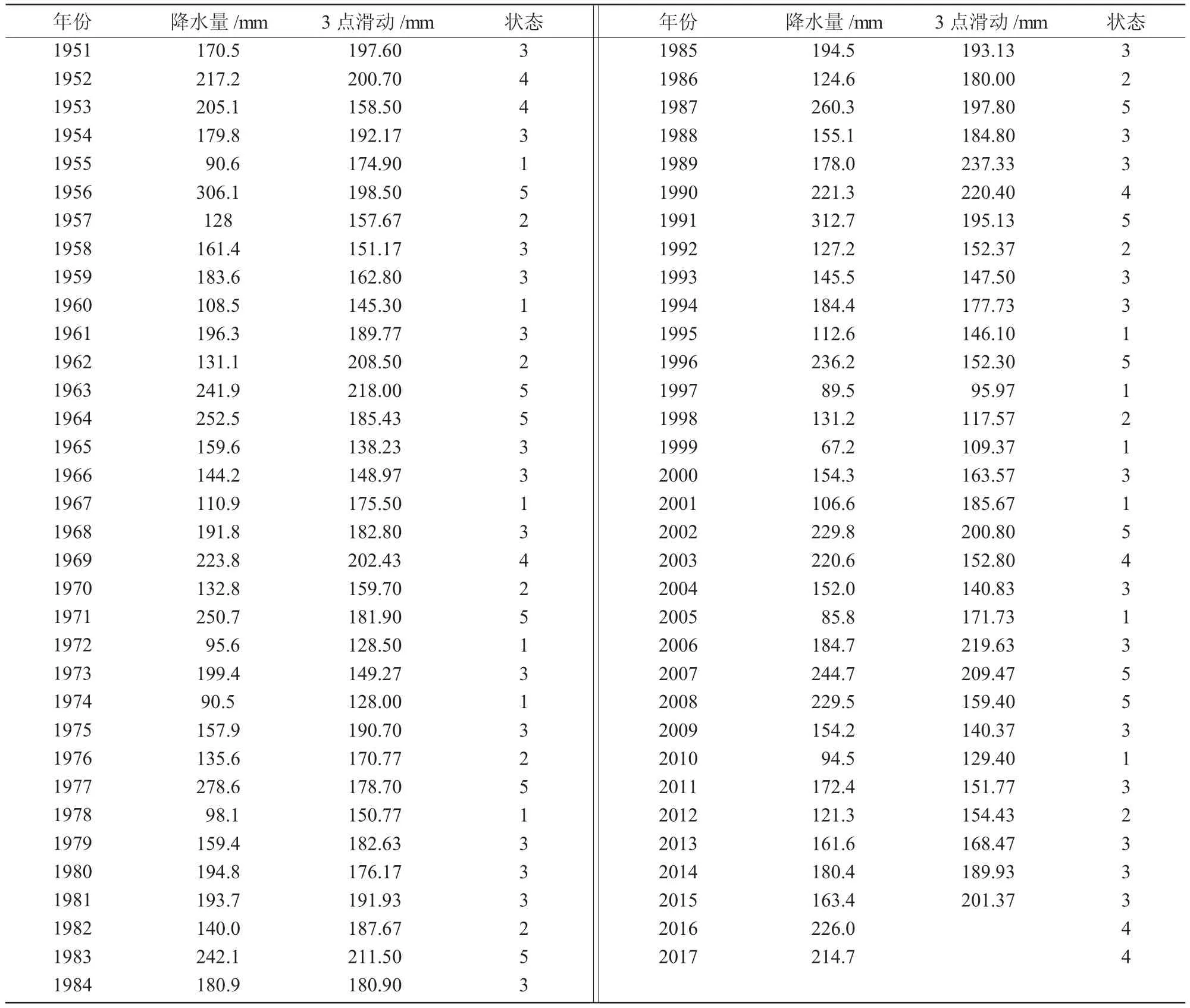
表2 太原市小麦生育期降水序列及状态

表3 太原滑动平均降水量等级划分

由预测量可知，未来降水量基本上都在一个状 态之间，存在下降趋势，但是下降趋势不明显。

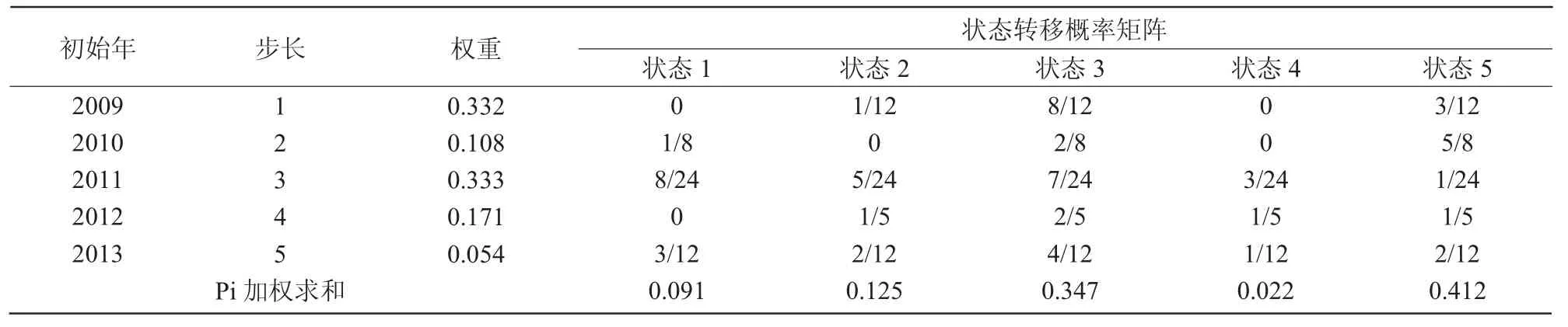
表4 2014年太原滑动平均降水量预测

表5 冬小麦生育期滑动平均降水量预测验证

表6 降水预测

3 结论与讨论

本研究利用华北冬麦区各站点近60 a的逐年降水数据资料，综合运用了线性趋势法、3点滑动平均法、Hurst指数分析、M-K非参数突变检验和加权马尔可夫链预测模型，对华北地区各站点及站点平均降水量的变化规律进行了研究与预测。

线性趋势表明，近年来，各站点小麦生育期降水量均略呈下降趋势，下降0.53～7.54 mm/10 a，与华北地区整体变化趋势表现一致[14]，这与张皓等[15]的研究结果一致。然而，孙燕等[16-17]研究认为，华北地区秋冬春季降水量无明显下降趋势。这可能是因为研究站点单一以及研究区域不同而引起的。

M-K非参数统计检验结果表明，近60 a来，太原、北京的小麦生育期降水量的突变可能发生在1981，1967年，与张磊[18]研究整个北方地区的降水突变年份1972年有一定的误差，这是由于研究区域范围不同引起的，同时由于小麦生育期降水量数据时间序列有限，以及未对降水量数据进行拆分，使天津、石家庄等部分地区的突变年份未明确，还有待更长时间序列上的验证。

华北地区小麦生育期各站点降水量的Hurst指数均大于0.5，表明未来下降趋势将继续持续，但由于各站点指数都接近0.5，说明持续性不强。

由加权马尔可夫链预测结果可知，该方法误差在50 mm左右，相对误差不超过20%，与其他学者结果大致相同[19-20]，适用于本地区冬小麦生育期降水量的预测。未来冬小麦生育期降水量基本上都在一个状态区间，大部分都在平水年间，比较预测年份之前的年降水量有小幅度的下降，以此验证了下降趋势但持续性不强的结论。