重建单元知识结构 优化单元整体教学

【摘 要】在对教材分析的基础上提出“把三角形全等的几种判定方法放在一起集中探究，辨别分析后再集中运用”的整体教学思路，从教学内容前后对比分析、基于单元知识结构的课时教学设计、教学反思等方面分析，阐述整体构建单元知识结构的价值和意义，以提高学生整体运用知识的水平，增强综合运用能力，渗透核心素养，提升课堂教学效率。

【关键词】单元知识结构;教学分析;教学设计;教学反思

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2019）91-0035-03

【作者简介】张绍俊，江苏省清江中学（江苏淮安，223001）教师，高级教师，淮安市学科带头人。

当前的数学课堂教学大多是根据教材的安排，按照课时知识点进行教学，这样容易导致所学知识点以碎片化的形式进行存储，不易形成单元整体知识结构，学生较难形成综合运用能力。作为教师，应从整体化、系统化的高度进行单元知识整体结构设计，优化单元整体教学，凸显教师的主导地位。

《义务教育数学课程标准（2011年版）》明确指出，“教材的编写要有利于调动教师的主动性和积极性，有利于教师进行创造性教学”。教材是课程的载体，是重要的教学资源，承载着编写者对课程理念和教学思想的理解，但它不一定满足教学情境变化了的教学实际。教师既要充分应用教材组织教学，同时又不能盲目依赖教材。

从“教教材”到“用教材教”，既是新课标的重要理念更是教师教学主导性的体现。笔者在“探索三角形全等的条件”单元教学中，运用单元知识结构整体教学模式的相关理论，重建单元知识结构，有效提高教学效率，促进学生综合解题能力和核心素养的提升。

一、教学内容分析

“探索三角形全等的条件”是苏科版教材八年级上册第一章第三节的教学内容。教材对于三个基本事实的探究学习按照以下统一模式进行：先用尺规作图作符合要求的三角形，然后验证所作三角形是否重合（全等），进而得出判定两个三角形全等的三个基本事实（SAS、ASA、SSS），最后通过相关例题对所学的判定方法进行巩固运用。关于全等判定的“AAS”，教材安排在学习“ASA”之后，作为它的推论证明并运用;在一般三角形全等的判定方法之后，再通过构造全等直角三角形，证明得出两个直角三角形全等的判定定理，即“斜边、直角边”或“HL”。

教材这样的结构安排主要是围绕知识点依次进行教学设计，学生每课时学习掌握一种判定方法，虽然后面的学习内容也不断融合前面的知识，体现螺旋上升的基本设计思路，但总体上学生形成的是零散碎片化的知识，学生对比选择、综合运用的能力达不到应有的高度，尤其在遇到比较复杂的图形时，学生往往无从下手、无所适从。

从单元结构的视角看，课堂教学过程不仅要让学生掌握“形式化”的“明述知识”，更应注重体现思维能力的“默会知识”的培养。基于这样的认识，在具体的教学实践中，笔者首先把每课时都有的“作图+验证+基本事实的归纳”整合在一节课进行，让学生集中了解判定三角形全等的三个基本事实，以及由“ASA”推证出来的“AAS”定理，初步认识判定三角形全等的基本方法和主要思路。这样设计的主要理由是：把同类问题放在一起进行集中探究，有利于学生在“最近发展区”进行学习，能达到触类旁通、融会贯通、举一反三的效果，更利于学生感受方法的多样性和数学思想方法的魅力。其次是4种判定方法的简单运用和解题的规范化要求，学生在初步运用过程中逐步辨析4种判定方法的条件、位置关系以及它们的异同，最终理解掌握4种判定方法，实现由“明述知识”到“默会知识”的自然迁移。最后再依托题组进行综合运用训练，重在思路的分析和方法的选择，凸显思维能力要求。笔者的设计和按课时知识点组织教学相比，不仅完成教学任务的时间变短（由原来的5课时缩短为4课时），而且有助于培养学生辨别理解判定方法并灵活选择运用判定方法解题的能力。

二、课时教学设计

根据重建的单元知识结构，“探索三角形全等的条件”（一般三角形）整体设计安排四课时。以第一课时为例设计如下。

第一课时：三角形全等的4种判定方法的整体认识。

【教学目标】会用尺规作图按要求作三角形;在操作探究过程中认识三个基本事实及“AAS”;经历探索三角形全等的条件的过程，学习分析问题的方法，积累数学活动的经验。

【教学重难点】掌握用尺规作图作三角形的方法;初步理解三个基本事实和“AAS”;四种判定方法的区别。

主要教学过程如下：

1.問题引入。

（1）能够完全重合的两个三角形是全等三角形，那么要判定两个三角形全等一定要把两个三角形叠放在一起，看它们是否重合吗？有没有比较简单的方法？

（2）当两个三角形的一对边或角相等时，它们全等吗？当两个三角形的两对边或角分别相等呢？

（3）请你猜想一下，两个三角形满足几个条件时可能全等？

（设计意图：第一个问题是让学生感受到探究三角形全等条件的合理性和必要性，增强本节课学习的兴趣和愿望;第二和第三个问题是引导学生从不同角度去寻求解决问题的方法和策略，体会合理猜想是探究数学问题的一个基本策略。） 2.问题探究。

（1）操作活动一：用尺规作图作△ABC，使∠A=∠α，AB=a，AC=b。按下列作法作图：①作∠MAN=∠α;②在射线AM、AN上分别作线段AB=a，AC=b;③连接BC。△ABC就是所求作的三角形。接着将△ABC剪下来，同桌的两人将剪下来的三角形叠合。

将所作三角形剪下来与其他同学进行比较，你发现了什么？说明了什么问题？

归纳结论：两边及其夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）。

（设计说明：让学生经历动手作图、裁剪、叠合等过程，感受数学来源于生活，体会知识的来龙去脉及相互关系，从而易于认识、理解知识，并为知识的运用做好铺垫。）

（2）操作活动二：按所列作法，用尺规作图作△ABC，使AB=a，∠A=∠α，∠B=∠β。

根据同样的操作探究过程，分析归纳可得：两角及其夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）。

（3）操作活动三：按所列作法，用尺规作图作△ABC，使AB=c，AC=b，BC=a。

根据同样的操作过程，分析归纳可得：三边分别相等的两个三角形全等（可以简写成“边边边”或“SSS”）。

（设计说明：在操作活动一的基础上类比进行操作活动二、三，详略得当，衔接自然，有利于知识的生成，符合学生的认知规律。三个基本事实形成一个知识模块，有利于学生整体认知、辨别和对比。）

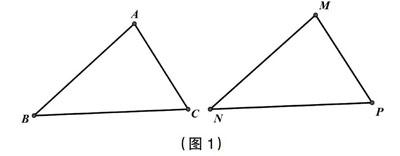
（4）问题思考：如图1，在△ABC和△MNP中，∠A=∠M，∠B=∠N，BC=NP，那么△ABC和△MNP全等吗？为什么？

根据“ASA”可得基本事实（ASA）的推论：两角分别相等且其中一组等角的对边相等的两个三角形全等（可以简写成“角角边”或“AAS”）。

（设计说明：将判定三角形全等的“AAS”以问题形式呈现给学生，激发学生的思考兴趣，同时通过“两角和一个边”的条件分析，自然而然与“ASA”联系起来，再运用化归思想证明推论“AAS”的成立。）

三、基于单元知识结构的教学反思

1.突出整体知识建构，促进单元教学目标达成。

“单元结构教学”就是根据知识的发生规律、内在的联系，将数学知识和教学内容进行优化重组，构建新的教学单元或教学模块，通过对新的教学单元的学习，掌握应有的知识，形成必备的能力，有效实现单元整体教学目标。本单元教学设计时没有按照书本的编排顺序，即每一个判定方法（基本事实和推论）都安排一个课时进行探究归纳、例题练习和巩固运用，而是整体呈现单元内容，即第一节课的重点是通过作图比较，猜想归纳四种判定方法，让学生整体感知并进行对比理解，不作运用方面的要求。在后续课时中再进行例题教学，由简单到综合的巩固运用，这样突出了不同课时的教学重点，也有利于课时教学目标和单元目标的达成;特别是能让学生整体理解知识，运用整体的思路去分析解决问题，形成整体的知识结构，提升综合运用能力。

2.渗透数学思想，培养核心素养。

重构知识单元，就是将三个基本事实放在一起进行探究归纳，通过类比形成三种判定方法，渗透了数学中的类比思想;同时，四种判定方法都是由图形中的某些数量关系判断图形的位置关系，体现了数形结合的数学思想。同一个图形，不同的条件需要选择不同的判定方法，渗透分类讨论的数学思想。在日常的教学活动中，教师要精心设计知识单元，优化整体结构，将数学思想渗透到教学活动中去，使学生不断积累数学活动经验，提升数学核心素养。

3.关注个体差异，注重分层要求。

由于每个学生的学习成绩、学习动力、学习兴趣、学习态度、学习方法以及学习和成长环境不同，他们的个性习惯、兴趣爱好也不相同，面对同样的数学问题所表现出来的悟性和接受能力也大不相同。特别是全等三角形的四种判定方法一起学习、一起辨别运用时，对一些学习基础薄弱、综合运用能力不强的學生难度显得更大些，甚至个别学生看到问题无从下手、无所适从。因此，在教学设计安排时，第二课时“简单运用”的起点应适当低一些，速度适当放慢，遵循“低起点、小坡度、密台阶”的基本原则设计训练题组，即使是第三、第四课时的“综合运用”也要把握问题的难度，对不同层次的学生提出不同的要求。不关注个体差异，盲目贪多求难，往往适得其反。

【参考文献】

[1]徐文彬，李永婷，安丹诺.单元知识结构整体教学设计模式的理论建构[J].江苏教育：中学教学，2018（6）：7-9，22.

[2]费祯红，刘乃至.突出课时重点，整体设计单元教学——以“幂的运算”单元教学起始课为例[J].中学数学教学参考（中旬），2018（9）：60-63.

[3]顾大权.渗透整体意识，完善思维结构[J].中学数学教学参考（中旬），2018（12）：36-39.