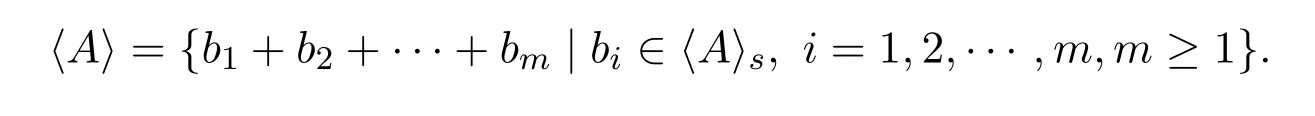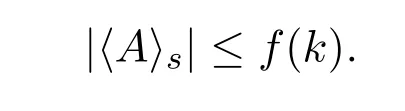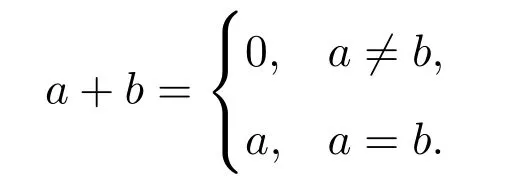关于加法幂等元半环簇的几个结果

2019-01-12任苗苗赵宪钟

纯粹数学与应用数学 2018年4期

任苗苗,赵宪钟

(西北大学数学学院,陕西西安 710127)

1 引言和预备知识

设 V是一个同型号的代数类,若V对类算子同态像,子代数和直积封闭,则称其为簇.由Birkho ff定理知一个同型号的代数类是簇当且仅当它是等式类,即,满足某个恒等式集合的代数的全体.设V是簇,如果存在有限的恒等式集合Σ使得Σ确定的等式类等于V,那么称V是有限基底的.否则,称V是非有限基底的.V的有限基底问题是问V是否为有限基底的.该问题也被称作Tarski基底问题,它是簇的经典问题之一,且是国际上一大批代数学家所热衷研究的问题.若一个代数生成的簇是有限基底的,则称其为有限基底的.否则,称其是非有限基底的.有限群[1],有限环[1]都是有限基底的.然而,有限半群[1]和有限半环[2]未必是有限基底的.

如果一个代数的每个有限生成的子代数是有限的,那么称该代数是局部有限的.进一步,若簇V的每个成员是局部有限的,则称V是局部有限的.1902年,Burnside[3]提出如下问题:满足恒等式xn≈1的群是否为局部有限的?该问题已成为群论中最重要的问题之一,到目前为止还没有被彻底解决.一般地,一个簇的Burnside问题是问这个簇是否为局部有限的.1952年,Green和Rees[4]证明了恒等式xn≈1确定的群簇和半群簇的Burnside问题是等价的.另一方面,一个簇的限制Burnside问题是问该簇的所有局部有限成员作成的类是否为它的子簇.

在簇的Burnside问题和有限基底问题的研究过程中,遗传非有限基底的簇发挥着非常重要的作用.具体地说,若一个局部有限的簇满足条件:包含它的每个局部有限的簇是非有限基底的,则称这个簇是遗传非有限基底的.换句话说,一个局部有限的簇是遗传非有限基底的当且仅当包含它的每个有限基底的簇都不是局部有限的.如果一个代数生成的簇是遗传非有限基底的,那么称其是遗传非有限基底的.从而得到,若一个簇是遗传非有限基底的,则可以回答一些与之相关的簇的Burnside问题和有限基底问题,即包含这个簇的每个有限基底的簇不是局部有限的,且包含它的每个局部有限簇是非有限基底的.特别地,一个遗传非有限基底的簇一定是非有限基底的.本文将给出关于加法幂等元半环簇的有限基底问题和Burnside问题的两个结果.

设(S,+,·)是(2,2)型代数,若加法导出(S,+)是交换半群,乘法导出(S,·)是半群,且(S,+,·)满足恒等式

则称(S,+,·)是半环,简记为S.半环是环和分配格的共同推广,它在几何学,理论计算机科学和信息科学领域有着广泛的应用.若半环满足恒等式x+x≈x,则称其为加法幂等元半环,也被称作半格序半群.分配格,半群的幂半环,集合上的二元关系半环,max-plus代数以及半格的自同态半环都是加法幂等元半环.反之,每个加法幂等元半环可嵌入到某个半格的自同态半环中.为了方便叙述,引入下列符号:设m和n是正整数,且m

在过去的20年中,国际上关于加法幂等元半环簇的研究是相当活跃的.1978年,McKenzie和Romanowska[5]证明了Sr(2,1)的满足恒等式xy≈yx的子簇都是有限基底的.本世纪初,Zhao,Guo和Shum[6]证明了Sr(2,1)的与格林关系相关的一些子簇是有限基底的.在此基础上,2005年,Pastijn,Zhao和Ghosh[7-8]证明了Sr(2,1)的每个子簇是有限基底的.2017年,Ren,Zhao和 Wang[9]证明了 Sr(3,1)的每个子簇是有限基底的.此外,Gajdo和 M.Kuil[10]证明了当m≥2时,Sr(n,m)不是局部有限的;Sr(n,1)是局部有限的当且仅当G(n,1)是局部有限的,从而表明了群簇G(n,1)的Burnside问题与加法幂等元半环簇Sr(n,1)的Burnside问题是等价的.

2 主要结果

命题 2.1设S是加法幂等元半环,则S是局部有限的当且仅当(S,·)是局部有限的.

证明设A是S的任意非空子集,分别表示S的由A生成的子半环和(S,·)的由A生成的子半群.由于中的每个元素可表示为A中有限个元素的乘积,且S的乘法对加法满足左右分配律,容易验证,

由命题2.1知一个加法幂等元半环的Burnside问题和它的乘法导出的Burnside问题是等价的.由文献[1](定理1.4.37)得到了一般的局部有限簇是遗传非有限基底的一个充分必要条件,即下列结果:

命题2.2设V是局部有限的加法幂等元半环簇或半群簇,则V是遗传非有限基底的当且仅当对于任意的n≥1,存在有限生成的无限代数An使得An的每个n-生成子代数是V的成员.

定理2.1设S是局部有限的加法幂等元半环,若S是遗传非有限基底的,则(S,·)是遗传非有限基底的.

证明设 W 表示半环S生成的加法幂等元半环簇,Ws表示半群(S,·)生成的半群簇.若S是遗传非有限基底的,则由定义知W是遗传非有限基底的半环簇.进一步,由命题2.2知对于任意的n≥1,存在有限生成的无限加法幂等元半环An使得An的每个n-生成子半环是W的成员.设Bn是An的任意有限生成元集,即.则由命题2.1的证明知的每个n-生成子半群是W的某个成员的乘法导出的子半群.由于W的每个成员的乘法导出是Ws的成员,可得的每个n-生成子半群是Ws的成员,且由命题2.1的证明知是有限生成的无限半群.再次利用命题2.2可得Ws是遗传非有限基底的,由定义知(S,·)是遗传非有限基底的.

定理2.1的逆命题是否成立是未知的,目前文献中尚未有刻画遗传非有限基底的加法幂等元半环簇的结果.另一方面,定理2.1,若一个法幂等元半环的乘法导出不是遗传非有限基底的,则该半环不是遗传非有限基底的.又由文献[11]的主要结果可得,阶数小于6的半群都不是有限基底的,这蕴含着它们都不是遗传非有限基底的.从而得到一个有限遗传非有限基底的加法幂等元半环的阶数大于7,即下列结果成立:

推论2.1阶数小于6的加法幂等元半环都不是遗传非有限基底的.

然而,阶数小于6的加法幂等元半环的有限基底问题尚未被解决.特别地,到目前为止还没有发现阶数小于6的非有限基底的加法幂等元半环.因此,系统地研究小阶加法幂等元半环的有限基底问题是非常有必要的,这是后续工作的一个方向.众所周知,Zimin字在字的组合理论和半群簇的研究中发挥了非常重要的作用.具体地说,称如下归纳定义的字Zn为Zimin字:

由文献[1](定理3.6.34)知有限半群S是遗传非有限基底的当且仅当对于任意的n,S不满足非平凡的恒等式Zn≈W.设T是Sr(n,1)中的任意有限成员,则(T,·)满足非平凡的恒等式.由上述结论得半群(T,·)不是遗传非有限基底的.进一步,利用定理2.1可得半环T不是遗传非有限基底的.由此得到下列推论:

推论2.2Sr(n,1)中的任意有限成员都不是遗传非有限基底的.

接下来将肯定地回答Sr(n,1)的限制Burnside问题.为此,需要文献[12](定理1),即下面的结果:

引理2.1设V是有限基底的半群周期簇,则存在递归函数f(k)是V中所有k-生成有限半群的基数的上界当且仅当V中所有的nil-半群是局部有限的.

定理2.2Sr(n,1)的所有局部有限成员的类作成簇.

证明由文献[1](问题3.10.4)可得,一个有限基底的簇V的所有局部有限成员的类作成簇当且仅当对于任意的k≥1,V中所有k-生成有限代数的基数存在上界.注意到Sr(n,1)是有限基底的.因此,为了证明Sr(n,1)的所有局部有限成员的类作成簇,仅需要表明对于任意的k≥1，Sr(n,1)中所有k-生成有限代数的基数存在上界.设是Sr(n,1)中任意k-生成有限半环,则由命题2.1的证明知是Sg(n,1)中k-生成有限半群,且