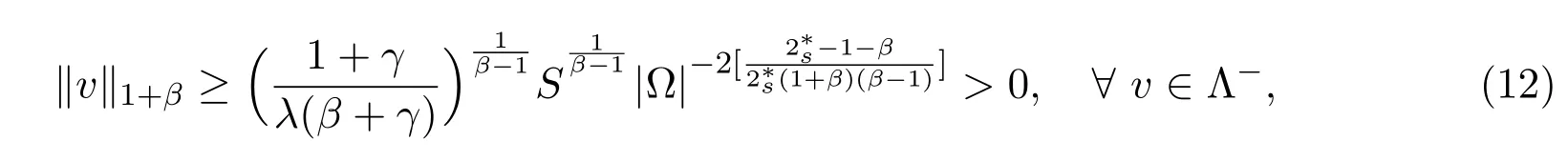Singular elliptic problems with fractional Laplacian

Wang Xing,Qin Xinqiang,Hu Gang,Wei Guo

(1.School of Science,Xi′an University of Technology,Xi′an 710054,China;2.Department of Mathematics and Computer Science,University of North Carolina at Pembroke,Pembroke North Carolina 28372,USA)

Abstract：In this paper,we deal with a class of singular elliptic problems with fractional Laplacian.Our results show the existence and multiplicity of weak positive solutions to singular elliptic problems when the parameter small enough.It is worth pointing out that since the testing functions without a compact support in our results,our method can be used to give a direct and simple proof of the existence of weak positive solutions for other singular fractional problems.

Keywords：topology,fractional Laplacian,nondifferentiable functional

1 Introduction

The fractional and non-local operators of elliptic type due to concrete real world applications in finance,thin obstacle problem,optimization,quasi-geostrophic flow etc[1].Caffarelli,Salsa and Silvestre studied free boundary problems for such operators in references[2-3].In this paper we are interested in the existence of weak positive solutions satisfying the following singular elliptic boundary value problem involving the fractional Laplacian

where Ω⊂RN(N≥3)is a bounded domain with smooth boundary∂Ω,N>2s(00 is a real parameter,a:Ω−→Ris a given non-negative non-trivial function belonging to some Lebesgue space.

By a weak solutionuof(1)we meanthat satisfies(1)weakly.More precisely,we are looking for a mapufrom Ω toRsuch thata.e.in Ω and

where

The principal feature of interest here is that the given boundary value makes the equation singular at the boundary∂Ω.

2 Preliminaries and main result

and the embedding is continuous but not compact if.We can define(see for instance references[6-7])

The following theorem is the main result of this paper.

Theorem 2.1Let Ω be a bounded domain in,a(x)∈L2(Ω)witha(x)≥0 in Ω.Then there exists a real numberλ∗such that for anyλ∈(0,λ∗)problem(1)possesses at least two weak positive solutionsin the sense(2).

Remark 2.1It is worth pointing out that we only assume the coefficient functiona(x)≥0.This greatly relaxed the request according toa(x)in reference[8].Here,authors requesta(x)has a uniform positive lower bound that is there exists a positive constantθ>0 such thata(x)≥θfor allx∈Ω.

3 Existence and multiplicity of weak positive solutions

In this section,the proof of theorem 2.1 is given.Let us define the Nehari manifold

Notice thatu∈Λ ifuis a weak positive solution of(1).The fact suggests to us that we can give the following splitting for Λ.

To obtain theorem 2.1,several preliminary results are needed.

Lemma 3.1There existsM>0 such that∥u∥≤M,∀u∈Λ+.

ProofLetu∈Λ+.From the definition of Λ and Λ+we have that

Thus we obtain

Obviously,the consequent of Lemma 3.1 follows from letting

This completes the proof of Lemma 3.1.

Lemma 3.2The functionalIλis coercive and bounded below on Λ+.

ProofSinceu∈Λ+,using the definition of Λ+and the inequality(4),it follows that

i.e.

for some positive constantsC1andC2.This implies thatIλis coercive and bounded below on Λ+.This completes the proof of Lemma 3.2.

Lemma 3.3The minimal value

ProofUsing the Hölder and fractional Sobolev inequalities(3)and(4),we have

and

Moreover,since 1−γ<1,we have that for allv>0,Iλ(tv)<0 providedt>0 is sufficiently small.This implies that.This completes the proof of Lemma 3.3.

For the sake of completeness,we are ready to give the following lemma about the embedding properties of.We are refer to references[4-5]and their references for a proof of it.

Lemma 3.4Lets∈(0,1)andp∈[1,+∞)such thatsp

Lemma 3.5For allλ∈(0,λ1),there existsuλ∈Λ+such that.

ProofLet{un}⊆Brbe a minimizing sequence such thatIλ(un)→mλasn→∞.Using the Lemma 3.1,there exists a subsequence of{un}(still denoted by{un})such thatun⇀uλweakly in,strongly in.According to Hölder inequality,we derive that asn→∞,

Using the Brezis-Lieb Lemma we obtain

and

Combining above arguments with(8)-(10),we can get

that is 0≥Iλ(uλ)−mλ+o(1)≥o(1).Passing to the limit asn→∞,we obtainIλ(uλ)=mλ.

It remains to show thatuλ ∈Λ+.It is sufficient to proveun→uλstrongly in.

From

we have

Sinceun⇀uλweakly in,by Lemma 3.4,we infer thatun→uλstrongly inL1+β(Ω),thusun→uλstrongly in.This completes the proof of Lemma 3.5.

3.1 Existence of weak positive solution uλ

Lemma 3.6The minimizeruλ(x)>0,for allx∈Ω.

ProofFor anywithϕ≥0 andt>0 small enough,sinceuλis a minimizer,we have

Dividing byt>0 and lettingt→0 therefore shows

Moreover,by the strong maximum principle for the nonlocal operator(−∆)s(the theorem 1.2 in reference[9]),we have

This completes the proof of Lemma 3.6.

From the Lemma 3 in reference[10],we can get the following lemma 3.7 and lemma 3.8 immediately.

Lemma 3.7For eachu∈Λ+,then there existsε>0 and a continuous function

satisfying that

Lemma 3.8For any given,there existsT>0 such that

Lemma 3.9The minimizeruλ ∈Λ+is a weak positive-solution of problem(1),i.e.,satisfying

ProofRecall the Lemma 3.8,we infer that for anyandt∈[0,T]there is

Hence,easy computations show that

Dividingt>0 and lettingt→0+which implies that

From simple arguments and Fatou’s Lemma,we infer that

Combining these relations we conclude that

into(11),we have

where

and

Since the measure of the set{x|(uλ+tϕ)<0}tend to 0 ast→0+,it means

Thus,dividing byt>0 we infer that

Hence

the conclusion follows.The proof of this lemma is completed.

3.2 Existence of weak positive solution vλ

Lemma 3.10There existsλ2>0,such that Λ−is closed infor allλ∈(0,λ2).

ProofWe claim that Λ0={0}.Arguing by contradiction,we assume there is ah∈Λ0and.From the definitions of Λ0and Λ,we have.

Therefore,we obtained

On the other hand,by using(4)and fractional Sobolev inequality,we infer that

where the constantC>0 independent ofλ.Since,it means that there existsλ2>0 small enough satisfying

Assume{un}⊆Λ−be a sequence satisfyingun→uin the.Using the Sobolvev inequalities and continuous compact embedding,we haveun→uinandu∈Λ−∪Λ0.Recall the definition of Λ−once more,we infer that

Lemma 3.11There existsλ3>0,such thatIλ(u)≥0,for allu∈Λ−whileλ∈(0,λ2).

ProofSuppose,by contradiction there is aυ∈Λ−such thatIλ(v)<0,that is

By the definition of Λ−,it follows that

combining(4)we have

Lettingλ→0+,infer that,which is a contradiction with inequality(12).This

completes the proof of Lemma 3.11.

By the Lemma 3.11,the definition

is well defined.

Lemma 3.12There existsλ4>0 small enough such that for allλ∈(0,λ4),there existsvλ∈Λ−satisfying.Moreover,vλis a weak positive solution of problem(1).

ProofWe start by claim thatIλis coercive on Λ.In fact,for anyv∈Λ,we get

where the last Stepwe have used the inequality(4).ThusIλis coercive on Λ,it is also true for Λ−.Assume the sequence{vn}⊆Λ−satisfyingasn→∞.Using the coercive ofIλ,we derive that{vn}is bonded in Λ−.Thus we can assume thatvn⇀vλweakly asn→∞in Λ−.Recall Λ−is completed in(Lemma 3.10),following the same arguments as in proving the existence of minimizeruλ(Lemma 3.5)and the compactness of the embeddingwe obtainvλ∈Λ−is the minimizer ofIλ.Moreover,arguing exactly as in the proof of weak positive solutionuλ(Lemma 3.9),one can prove thatis also a weak positive solution for problem(1).This completes the proof of Lemma 3.12.

Proof of Theorem 2.1Lettingλ∗=min{λ1,λ2,λ3,λ4},it is easy to verify directly that Lemma 3.1 and Lemma 3.12 are true for allλ∈(0,λ∗).Therefore,it follows from Lemma 3.9 and Lemma 3.12 thatuλandvλare the weak positive solution of problem(1).This completes the proof of Theorem 2.1.