培养学生数学核心素养的九年级教学实践——以“反比例函数”复习课为例

☉安徽省宣城市第六中学 葛福寿

一、问题提出

九年级新课结束后，学生还要在中考前进行一两轮的复习，其中复习课是提高学生学习能力的关键.复习既要巩固、消化数学基础知识，进一步提高学生分析问题、解决问题的能力，又要查缺补漏、归纳解题方法，吃透中考考点及常见题型，深化对知识的提升，提高复习效果.本文以“反比例函数”复习课为例，探讨、构建并完善九年级数学有效复习的模式，结合新课改下数学核心素养的渗透，谈如何才能激起学生在数学复习课上的兴趣，让他们形成完整的知识体系，提高他们运用知识、解决问题的能力，谈高效的中考数学复习课的设计策略，以期抛砖引玉.

二、设计思路

反比例函数是函数的重要知识，是中考必考内容，核心知识是反比例函数的概念、图像、性质与应用.从学生学习情况分析，反比例函数的增减性与一次函数的增减性容易混淆，用函数观念看待方程、不等式、函数间的关系，在理解上、思维方式上存在一定困难，用反比例函数解决实际问题需要建模的思路与策略，需要一定的生活背景知识，对学生有较高要求.基于以上分析，以学习函数最本质的思想——数形结合思想为立意，设计脚手架——函数图像，在课堂探究的过程中，加深对反比例函数的理解，以期达到本节复习课的教学目标.

三、教学过程

教学环节一：师生合作，“温故”核心知识

1.观看微课，整理核心知识

考点1：反比例函数的概念.

考点2：反比例函数的图像与性质.

函数的图像：

表1

函数的性质：

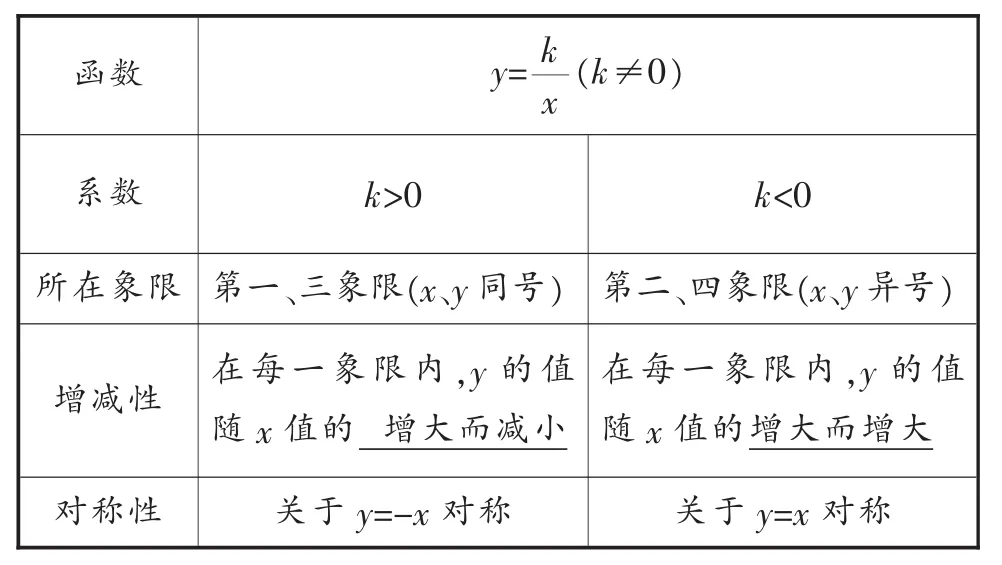
表2

k的几何意义：

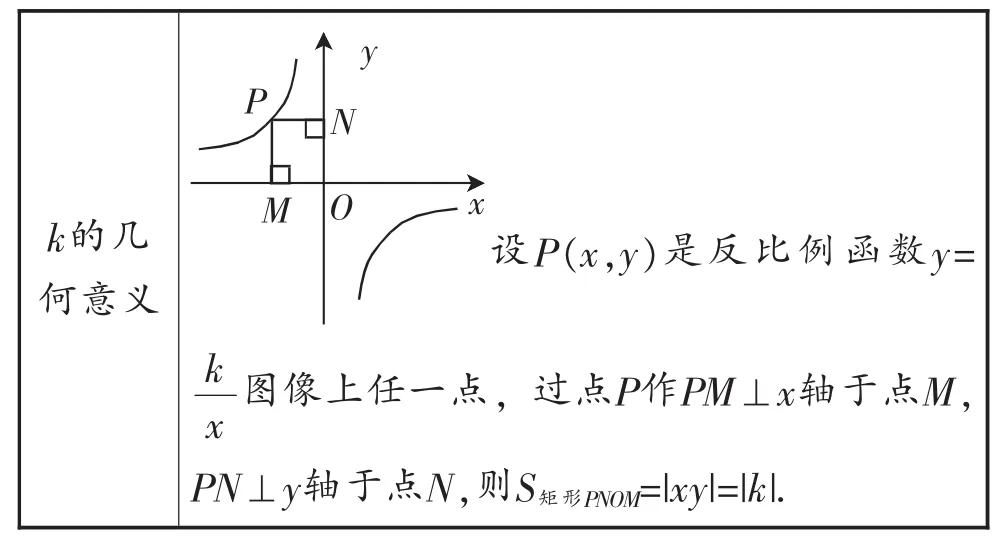
表3

考点3：反比例函数解析式的确定.

求解析式的一般步骤：

（2）根据已知条件列出含k的方程；

（3）求待定系数k的值；

求解析式的两种途径：

（1）根据问题中两个变量间的数量关系直接写出；（2）在已知两个变量x、y具有反比例关系y=（x≠0）的前提下，根据一对x、y的值，列出一个关于k的方程，求得k的值，确定出函数的解析式.

考点4：反比例函数的应用.

利用反比例函数解决实际问题，首先建立函数模型.一般地，建立函数模型有两种思路：一是通过问题提供的信息，知道变量之间的函数关系，在这种情况下，可先设出函数的解析式y=（k≠0），再由已知条件确定解析式中k的取值即可；二是问题本身的条件中不确定变量间是什么关系，此时要通过分析找出变量的关系并确定函数的解析式.

设计意图：通过学生观察核心知识要点，帮助学生梳理中考考点，让学生建构知识框架，培养学生的数学抽象核心素养.

2.结合核心内容，整理出中考试题与之相关的情境要点

PPT：呈现中考试题“要点”（见表4）.

表4 安徽中考试题“要点”

设计意图：通过整理近10年安徽省中考数学试题中考查的核心“要点”，让学生明确复习的方向，及时查漏补缺，养成良好的学习习惯，为学生升入高中的学习奠定基础，培养学生的数学综合素养.

教学环节二：师生探究，复习新知

（一）考点互动探究，基础训练

1.反比例函数的图像和性质

A.1 B.2 C.-2 D.-1

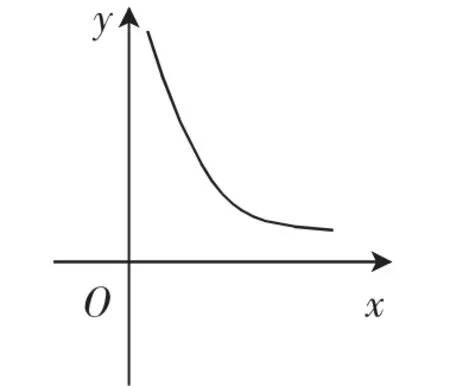
图1

（3）（2017年天津）若点A（-1，y1）、B（1，y2）、C（3，y3）在反比例函数的图像上，则y1、y2、y3的大小关系是（ ）.

A.y1＜y2＜y3B.y2＜y3＜y1C.y3＜y2＜y1D.y2＜y1＜y3

2.反比例函数的对称性

（2015年兰州）点P（1x1，y1）、P（x2，y2）在反比例函数y=（k＞0）的图像上，若x1=-x2，则（ ）.

A.y1＜y2B.y1=y2C.y1＞y2D.y1=-y2

3.反比例函数与方程不等式

A.1＜x＜6 B.x＜1 C.x＜6 D.x＞1

图2

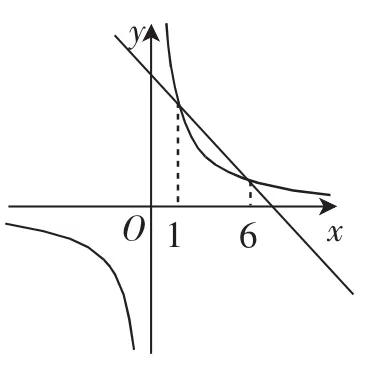
图3

变式：图3是反比例函数y1=和一次函数y2=mx+n的图像，若y1＞y2，则相应的x的取值范围是______.

4.反比例函数中k的几何意义

（1）（2015年齐齐哈尔）如图4，点A是反比例函数图像上一点，过点A作AB⊥y轴于点B，点C、D在x轴上，且BC∥AD，四边形ABCD的面积为3，则这个反比例函数的解析式为______.

图4

图5

（2）（2015年孝感）如图5，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数y=的图像上.若点B在反比例函数y=的图像上，则k的值为（ ）.

A.-4 B.4 C.-2 D.2

设计意图：从基本问题出发，层层深入，不断变式，让学生掌握函数值大小比较，学会从特殊到一般的研究方法，体会借助图像，利用数形结合思想解题.设计利用图像法解不等式，让学生经历观察、发现、比较、抽象的过程，从而更好地认识函数、方程、不等式三者间的关系，开阔学生的思维.既让学生掌握基本内容，又达到训练的目的，且能使题型设计层层深入，有梯度、有层次，提升学生的科学素养.

（二）考点互动探究，典例剖析

（2012年安徽第21题，12分）甲、乙两家商场进行促销活动，甲商场采用“满200减100”的促销方式，即购买商品的总金额满200元但不足400元，少付100元；满400元但不足600元，少付200元……乙商场按顾客购买商品的总金额打6折促销.

（1）若顾客在甲商场购买了510元的商品，付款时应付多少钱？

（2）若顾客在甲商场购买商品的总金额为x（400≤x＜600）元，优惠后得到商家的优惠率为p（p=，写出p与x之间的函数关系式，并说明p随x的变化情况；

（3）品牌、质量、规格等都相同的某种商品，在甲、乙两商场的标价都是x（200≤x＜400）元，你认为选择哪家商场购买商品花钱较少？请说明理由.

设计意图：函数是研究现实世界变化规律的重要内容和数学模型，设计反比例函数应用题，让学生经历问题情境→建立模型→求解的过程，同时进一步体会数形结合思想的价值，培养学生建模的数学核心素养.

（2011年安徽第21题，12分）如图6，函数y1=k1x+b的图像与函数y2=（x＞0）的图像交于A、B两点，与y轴交于C点.已知A点的坐标为（2，1），C点的坐标为（0，3）.

（1）求函数y1的表达式和B点的坐标；

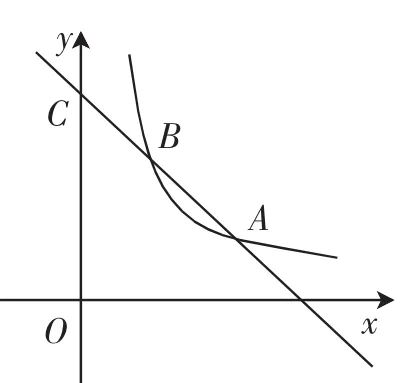
图6

（2）观察图像，比较当x＞0时，y1和y2的大小.

设计意图：本题主要是一次函数和反比例函数的综合应用，此类题目在中考中很常见，让学生通过小组交流加深对本习题的理解，提升学生分析问题、解决问题的能力，提高学生的综合数学核心素养.

教学环节三：复习训练，巩固提高

（2018年安徽第13题，5分）如图7，正比例函数y=kx与反比例函数y=的图像有一个交点A（2，m），AB⊥x轴于点B，平移直线y=kx使其经过点B，得到直线l，则直线l对应的函数表达式是_________.

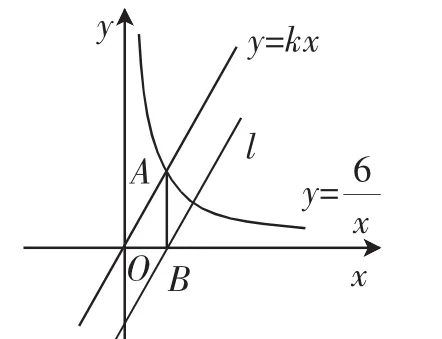
图7

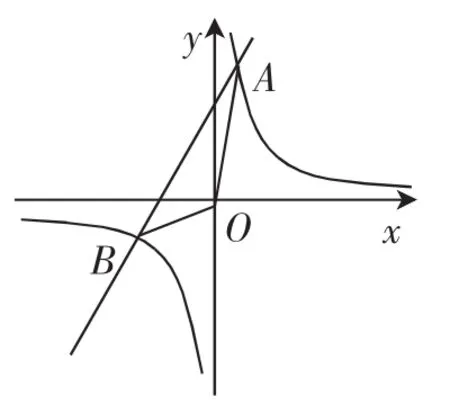
图8

（2015年安徽第21题，12分）如图8，已知反比例函数y=与一次函数y=kx＋b的图像交于点A（1，8）、B（-4，2m）.

（1）求k1、k2、b的值；

（2）求△AOB的面积；

（3）若M（x1，y1）、N（x2，y2）是比例函数y=的图像上两点，且x1＜x2，y1＜y2，指出点M、N各位于哪个象限，并简要说明理由.

设计意图：从函数图像出发，到函数解析式，再到结合图像上点的特征，完成了对函数图像与解析式的相互转化，蕴含了从数与形两个角度审视同一问题的观点，是数形结合思想方法的完美体现.通过这两题的练习，让学生了解中考的出题动向，增强学习的信心和勇气.

教学环节四：自我评价，反思内化

1.总结

（1）这节课主要复习的内容、方法有哪些？

（2）你有哪些收获？

2.分享收获

一种思想：数形结合思想（用数表达，用形释义）；

两种性质：增减性、对称性；

三种应用：比较大小问题，方程、不等式、函数问题，实际问题.

设计意图：学生自我反思，自我整理，教师根据学生的小结，展示归纳好的有关反比例函数的几点收获.变教师“一言谈”为学生的“群言谈”，这有助于学生概括能力、抽象能力、表达能力的提高.教师展示的提炼式归纳起到画龙点睛的作用，易于学生理解.

四、课后反思

本节课能达成预定的目标，教学方法和手段合理，前后过渡自然，同时关注到师生间的合作，没有以问代灌.但在某些问题提出后留给学生思考的时间不够长，在今后的教学中，要加强课堂习题的精选，注意备课的精细化，留给学生更多思考的空间与时间，这样的课堂才是顺畅型课堂、高效型课堂.

数学学科核心素养的培养不是一蹴而就的，核心素养之间的关系也不是彼此独立的，这就需要我们不断在教学实践中，以数学教学内容为载体，将数学知识与技能的学习、数学思想观念的建构、科学探究与解决问题能力的发展、创新意识等方面的要求融为一体，形成完整的数学学科核心素养体系.W