给学习动力，让思维飞翔——一节“规律探究”课的教学过程与点评

☉山东省东营市实验中学 曲艺慧

☉山东省东营市实验中学 王 莹

学生的学习动力来源于对问题的兴趣、积极的参与和探索的收获，调动学生“学”的兴趣，激发学生“思”的潜能，才能让学生的思维尽情翱翔.下面是一节初三的专题课“规律探究”，展示了教师的教学思路和学生的活动过程，让我们一起来感受其精彩，点评其得失.

一、报数游戏导入

师：咱们做一个游戏，我说出一组数，大家来报下面的三个数.看谁反应快！

师：第1组：1，3，5，7.

生1（抢说）：9，11，13.

师：这组数有什么变化规律？

生1：前面的数加2是后面的数.

师：也就是依次加2.很好，下面你们不仅要报出接下去的三个数，还要回答它们的变化规律.会的请举手.

师：第2组：5，8，11，14.

（约80%的学生举手）

生2：17，20，23，依次加3.

师：第3组：4，9，14，19.

（几乎全部学生举手）

生3：24，29，34，依次加5.

师：第4组：1，4，9，16.

（约30%的学生举手）

生4：25，36，49，前面是1、2、3、4的平方，后面的应该是5、6、7的平方.

师：也就是连续整数的平方.

师：第5组：2，5，10，17.

（个别学生举手，教师建议小组交流）

生5：这4个数分别是1、2、3、4的平方加1，后面应该是5、6、7的平方加1，也就是26，37，50.

师：哦，它们的规律是：序号的平方加1.非常好，鼓励一下.

师：第6组看谁能找出来：2，6，12，20.

（学生面面相觑，教师建议小组合作，经过交流，有几个学生举手）

生6：30，42，56.它的规律好像是：加4、加6、加8，所以，后面3个数依次加10、加12、加14.

师：很好！你知道第100个数是什么吗？（生6不好意思地摇摇头）

师：（导入课题）我们今天就来探究如何寻找规律.（板书课题：规律探究）

点评：教师以游戏的形式导入，调动学生学习的兴趣，吸引学生的注意力；选题由易到难，使不同层次的学生都能参与其中.前三题几乎全员参与，学生积极性很高，而后三题思维量逐步加大，在教师的引导下，通过同学之间的互助交流完成，可以充分发挥优生的作用，取长补短，培养学生的合作意识.同时，教师的顺势总结，又在不经意间培养学生语言表达的简练与准确性，而适时的追问，在深化思维的同时，又激发了学生进一步探究的欲望.为下一步的教学做好铺垫.是一则成功的导入.

二、探究数列规律

师：我们首先探究数列的规律.（多媒体展示）

探究1：数列规律.

问题1：每组数列的第n项是什么？

（1）1，3，5，7，….

（2）5，8，11，14，….

（3）4，9，14，19，….

生6：第1题：2n-1.

生7：第2题：3n+2.

生8：第3题：5n-1.

（学生回答的同时，教师用多媒体展示结果）

（1）1，3，5，7，…. an=2n-1

（2）5，8，11，14，….an=3n+2

（3）4，9，14，19，….an=5n-1

问题2：在这三组数列中，每组数列相邻两数的差值有什么数量关系？

生：差值相等.

师：归纳1：当相邻两数的差值相等时，第n项是n的一次函数.

点评：探究1从开始的游戏数列入手，由于有刚才的铺垫，学生能比较顺利地找到数列的规律，用n表示出来.这里的关键是教会学生如何从同类规律中提炼方法，同时让学生感受从特殊到一般的过程.

建议1：引导学生发现：这些数列相邻两数的差是相同的，而这个“差值”就是一次项系数；

建议2：在这里加一道“学以致用：数列-3，1，5，9，…的第100项是______”.让学生体会“特殊—一般—特殊”的数学思想.

问题3：这三组数列中，每组数列相邻两数的差值又有什么数量关系呢？与第一种情况一样吗？第n项是什么？

（1）1，4，9，16，….

（2）2，5，10，17，….

（3）2，6，12，20，….

师：先自主探究再小组合作.

（教师巡视指导）

生9：对于（1），和第一种情况不一样，第n项是n2，相邻两数的差值是：3、5、7、….

师：如果再一次求差呢？差值是？

生：2.

师：也就是两次求差相等.第（2）题呢？

生10：第n项是n2+1，相邻两数的差值第一次是：3、5、7、…，第二次是2.

师：很好！第（3）组呢？

（没有举手的）

师：可转化为：1×2，2×3，3×4，4×5，….

生11：第n项是n（n+1），即n2+n.

（教师在学生回答的同时用多媒体逐题展示答案）

（1）1，4，9，16，…. an=n2

（2）2，5，10，17，….an=n2+1

（3）2，6，12，20，….an=n2+n

师：归纳2：当相邻两数二次作差差值相等时，第n项是n的二次函数.

点评：这组问题，教师采用先自主探究再小组合作的方式完成，可以培养学生的探究精神和合作意识.第（3）题教师通过转化的方式，化为乘积式，学生更容易看出规律，使难点得到突破，也让学生体会到，遇到自己不熟悉的问题，可以转化为熟悉的形式去解决，体现了解决数学问题时转化思想的应用，总体效果较好.但问题3的设置不符合学生的思维习惯，学生不易按要求回答.

建议1：把问题3分成两个问题：一是：第n项的表达式是什么？它是关于n的什么函数？二是：相邻两数的差值有什么特点？先引导学生探索出每组第n项的表达式，体会得到的都是二次函数，然后去探索它们相邻两数的差值有什么共同特点，再进行归纳，效果会更好.板书可以采用对比式.以（3）为例：

2 6 12 20

第一次求差： 4 6 8

第二次求差： 2 2

这样，学生很容易看出“二次求差差值相等”.

建议2：加一道“学以致用：3，7，13，21，…的第n项是什么”.让学生明白，即使不能直接看出它的规律，只要发现第二次求差差值相等，就可以用求函数解析式的方法求出第n项.当然，具体解决此题用时较多，教师只需引导学生说出思路即可.

三、探究图形规律

师：刚才我们研究的是数列的规律，下面我们来看图形的规律.

探究2：图形规律.

如图1，是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，…，第n（n是正整数）个图案由_______个基础图形组成.

图1

（学生思维活跃，教师让学生到讲台上展示自己的方法）

生12：老师，用函数行吗？

师：非常好，你说一下做法吧！

生12：第1个图是4，第2个图是7，第3个图是10，相邻两数的差都是3，所以是一次函数.设y=kx+b，将（1，4）和（2，7）代入，得到所以规律就是3n+1.

师：大家看，用函数的方法解决规律问题应该先判断差值是否相等，然后设解析式，用待定系数法求解，最后确定规律.

生13：他的方法太麻烦了！

师：那请你上来说说你的简单方法.

生13：你看图形的变化，第2个图比第1个图多了3个菱形，第3个图又比第2个图多了3个菱形，也就是比第1个图多2×3个，…，那么第n个图就比第1个图多（n-1）×3个，所以第n项是：4+3（n-1），即3n+1.

生14：我还有不同的方法！我们看（用手比画），横着的菱形，第1个图有2个，第2个图有3个，那第n个图横着就有（n+1）个；竖着的菱形，第1个图有2个，第2个图有4个，第n个图有2n个，所以第n个图共有菱形（3n+1）个.

生15（一副大家风范）：其实，我发现，差值都是3，一定是3n+几，只看第一项4=3×1+1，就知道是3n+1.当然，如果你不放心，可以验证.（大家为他的精彩发言鼓掌）

师：大家的方法都非常好，我们一起总结一下，遇到图形规律，我们有哪些方法？

方法提炼：

三种思路：将图形转化成数字问题；直接从图形变化找图形特征；用函数思想解决.

点评：本题的选题很典型，有代表性.教师采取的方法也很好，给学生提供了展示的平台，激发了学生参与的热情，打开了学生的思路，学生的发言也很精彩，思维活跃，从不同的角度解决了问题，非常好.最后，教师的提炼也比较到位，让学生明确了解决图形规律问题的常用方法，效果不错.

建议：提醒学生，猜出结论后要学会验证，并教学生如何验证.

学以致用：

（2013·南昌）观察图2中各图形上点的个数，若按其规律再画下去，可以得到第n个图形中所有点的个数为_______

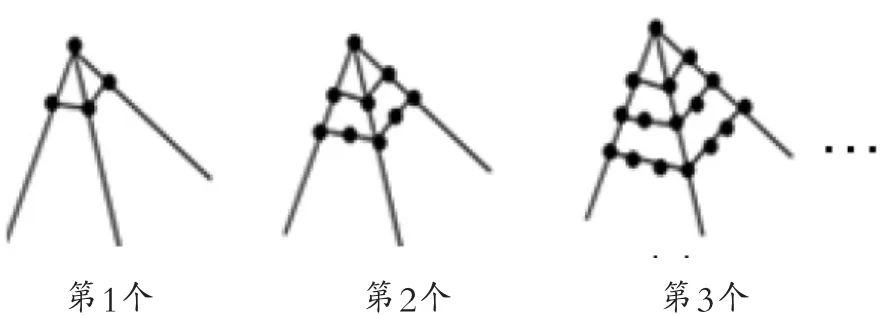
图2

生16：三个图所对应的数字分别是：4、9、16，可以看出这些都是平方数，分别是22、32、42，所以第n项是（n+1）2.

生17：我是根据图形的排列，发现第1个图可以看成2行，每行2个点，共2×2个点；第2个图是3行，每行3个点，是3×3；第3个图是4行，每行4个点，是4×4；所以第n个图有（n+1）2个点.

师：还有别的方法吗？

生18：也可以用函数解决.第1个图有4个，第2个图有9个，第3个图有16个，第4个图有25个，第一次作差之后是5、7、9，第二次作差之后是2、2，说明两次作差值相等，所以应该是二次函数.设y=ax2+bx+c，将（1，4）、（2，9）、（3，16）代入求出a、b、c.

师：由于时间关系，咱就不求了，感兴趣的同学课后可以试一试.

点评：作为学以致用，选题与上题既有共同点，又有不同点，相同点是解决问题的思路相同，不同点是规律变化不同，第n项是关于n的二次函数，规律更不容易看出来.学生利用上题提炼的方法顺利解决了此题，所选用的方法：一是转化为数的问题，根据数的特点寻找规律；二是利用图形的变化寻找规律；三是用函数思想解决，由于设的是二次函数，计算量较大，教师为了节省时间，只是引导学生说了思路，没有具体解决，习题的处理比较恰当，达到了巩固知识、熟练方法的目的.

四、综合运用，提升能力

师：如果我们把图形放在坐标系中，那么又有怎样的规律呢？请大家来思考一下这道题.

能力提升：

（1）求M1、M2、…、Mn的坐标.

（2）求S△P1M1M2+S△P2M2M3+…+S△Pn-1Mn-1Mn.

图3

师：先独立思考，再合作交流.（教师巡视指导）谁来回答？

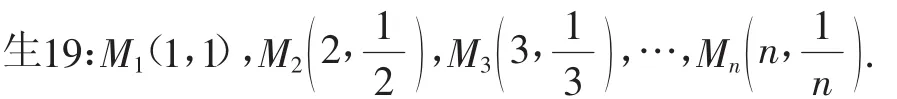
师：很好，第二问呢？（教师指定学生回答）

生20：我没算完.

师：那你计算到哪里了？

师：好，你先坐.谁能帮他解决这个问题呢？他算不下去的原因是什么？

生21：他不应该把前面的都乘开，所有三角形的底都是1，高分别是、…，到第n-1个是，所以面积应该是再把它们都加起来，提出×1，得到×1×），然后中间的项都抵消了，只剩下

师：从这道题可以看出，我们在做复杂的规律问题时，不要急于求出最终的结果，因为规律往往蕴含在计算的过程中，同时函数的规律问题我们最终也转化成了数列问题来解决.

点评：函数中的规律是本节课的难点，是数与形的综合考虑.此题教师的处理有两个成功点：一是对原题进行了适当改编，增加了第（1）问，降低了门槛儿，使大部分学生能入手去做；二是教师关注了学生的思维受阻点，在提问时有意识地提问了做题不顺利的学生（估计是教师在巡视时寻找的典型），引导其他同学帮助他找到突破的方法.进而得出“我们在做复杂的规律问题时，不要急于求出最终的结果，因为规律往往蕴含在计算的过程中”，处理得还是比较到位的.只是感觉在规律提炼方面略有欠缺.

建议：提醒学生，遇到规律问题中的多项求和，往往可以采用中间项抵消法，因此，要关注每一项是否可以写成“差”的形式.

师：刚才我们研究了这么多规律问题，下面请同学们独立完成这道中考压轴填空题.

如图4，点A1、A2、A3、…、An在抛物线y=x2的图像上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2013B2012B2013的腰长=______.

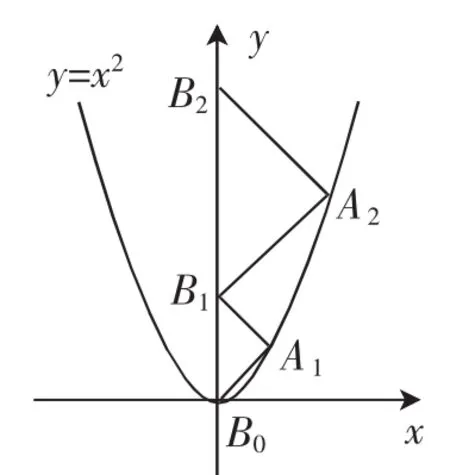
图4

（离下课还有2分钟，下课提醒铃声响起）

师：看来这道题难度有点儿大，同学们课后再解决.

点评：此题虽然也是函数中的规律问题，但与上面的题的思路不相同，学生做起来会有难度.由于时间关系，留作课后思考题，让学生有充分的时间思考交流，是可以的.只是希望老师下节课要引导学生把解决问题的方法提炼出来.

建议：通常遇到这类函数中的规律题，可结合函数解析式，求出函数图像上前三个点的坐标，然后求出目标线段的长.具体方法：

设A（1m，m），代入解析式y=x2，求出m=1，即第1个三角形的腰长是；

再设A（2n，n+2），代入解析式y=x2，求出n=2，即第2个三角形的腰长是2；

同理，设A（3a，a+6），代入解析式y=x2，求出a=3，即第3个三角形的腰长是3……

则△A2013B2012B2013的腰长=2013.

师：回顾一下我们这节课的学习，你都学到了什么呢？

生20：图形的规律可以看图形，也可以数个数.

生21：规律问题可以用函数的方法解决.

生22：复杂图形的规律不要着急求结果，要看过程.

师：很好！想一想，我们这节课用到了数学中的哪种思想方法啊？

生23：是不是转化？

师：非常好，我们这节课就是用的转化的数学思想，图形规律可以转化成数列规律，函数规律最终也可以转化为数列规律，然后我们用猜想与归纳的方法写出规律，这也是将来同学们高中要研究的不完全归纳法，大家到了高中会继续学习.

（板书设计）

点评：本节课的小结，教师采用的是：学生说出自己一节课的收获、教师提炼总结，再通过数学思想方法的渗透使认知得到升华，板书的设计也体现了本节课的要点，使知识更系统，这是一种很好的小结方法.

师：今天的作业：必做：学案第141页第1、3、4、6题，选做：学案第142页第9、10题.剩下的时间大家可以完成刚才那道题，也可以做今天的作业，如果还有问题可以与我交流一下.

点评：教师能做到对作业分层要求，这很好.第一，如果我们统一要求，一些学习困难的学生做不到，就只能抄袭作业或直接不做，反倒养成不好的学习习惯，还不如让他们集中精力做基本题，效果会更好些.第二，布置几道选做题给学有余力的学生，可以避免好学生吃不饱的情况，也可以深化他们的思维.

另外，一节课剩下几分钟让学生消化，给学生答疑，解决本节课遗留的问题，也是提高达成率的有效方法.

建议：可以给有余力的学生布置更个性化的作业，如：结合本节课大家的精彩发言写一篇小论文，或整理本节课的知识方法，这样或许能更好地培养他们的能力.

五、总评

本节课是关于规律探究的专题课.探索规律不仅是探索和发现数学规律，更主要的是让学生经历从特殊到一般、从一般到特殊这种探索与验证的过程，体会特殊—一般—特殊的数学思想.“学”的主角是学生，“思”的主角也是学生.要构建“学思课堂”，教师的作用就是：调动学生“学”的兴趣，激发学生“思”的潜能.

本节课的可取之处主要体现在以下几方面：

1.多种方式，调动学生的学习兴趣

热爱数学，对数学学习有自信，是学生学好数学的前提.因此激发学生兴趣，调动学生的积极性，就显得至关重要.本节课教师采取的三种方式达到了很好的效果：一是游戏导入吸引了学生的注意力，让学生带着兴奋和好奇开始本节课的学习；二是由浅入深的问题设置，使不同层次的学生都有思维空间，体会到解决问题的成功感，使全体学生有了参与的兴趣；三是给学生提供了展示自我的平台，不仅拓展了学生的解题思路，激发了学生的学习热情，而且展示的学生非常享受别人佩服的目光，很愿意把自己独特的解法与大家分享，也提高了大家学习数学的兴趣，增强了学好数学的信心.

2.合理引导，鼓励学生积极参与

学习是学生主动建构知识的过程，它不是简单的灌输，而主要依靠由内到外的自我生成.学生要获得数学知识，发展数学能力，就需要经历独立思考的过程.很多老师费心费力地从各种不同解题思路中优选最精彩、最简单的解题方法，在课堂上非常卖力地讲给学生，但学生不领情，讲过的照样不会，考试照样错.为什么？就是因为学生没有经过自己的思考，没有在大脑中留下深刻的印象.本节课通过教师的精心设计，以问题牵引的形式，让学生参与了整个知识的生成过程，几乎所有的问题、习题、总结，都是在教师的引导下，学生通过自己的独立思考，或通过生与生之间的合作交流完成的.他们参与了知识和方法的探究、发现和总结的全过程，当然印象会更深刻.在教学中教师适时引导学生发现、概括，完成新知识的建构，是提高课堂效率、提高教学成绩的有效方法.

3.精心设计，开发学生的思维潜能

本节课教师非常注重对学生思维能力的开发和培养.主要表现在以下几点.一是通过精选习题，培养学生思维的灵活性.本节课的选题非常典型，有代表性，虽然处理的习题不多，但每道题的处理都能达到举一反三的效果，通过“一题多解—提炼方法—学以致用”，学会从不同的角度解决问题，使思维更灵活.二是让学生讲题，培养学生思维的条理性.要给大家讲明白，把自己探究解决问题的策略展示给大家，首先自己的思维要非常清晰、有条理，同时，他的讲解对其他同学的思路也会有启发，在彼此思维的碰撞中，不仅拓展了大家的解题思路，还使彼此的思维都得到发展.三是能正视问题，帮助学生突破思维受阻点.学生在解决问题时遇到阻碍无法前进，这很正常.教师没有绕过问题，而是有意识把问题展现给大家，通过分析思维受阻的原因，教学生如何化解问题，教他们解决问题的方法，使思维受阻点得到顺利突破.四是通过分层递进，开发学生的思维潜能.本节课，在内容上采用按层次推进、逐步深化、螺旋上升的形式.无论是教师提出的问题，还是设置的习题，都注意了思维的梯度，关注学生的思维最近发展区，层层深入，使不同层次学生的思维都得到有效的训练.

4.把握机会，培养学生的合作意识

每个学生的生活经验、学习习惯及思维方式不同，合作交流为学生提供了一个展示思考结果的机会和平台，通过大家的相互讨论，学生对知识的理解会更全面、更深刻.使学生形成积极主动的学习态度，培养当今社会所需要的合作意识和合作能力.但如果内容选择不恰当，指导和要求不到位，往往“合作”变“聊天”，“交流”变“放松”，反而使部分学生养成懒散的习惯，学习效率大大降低.因此，哪些内容需要合作，怎样合作，教师要把好关.本节课教师选择的小组合作的内容都有一定的思维量，靠个人能力完成的很少，用小组合作的方式可以充分发挥优生的作用，有利于学生之间互相帮助，取长补短，还是比较合适的.在合作的同时，教师及时巡视指导，一可以帮助学习困难的学生，解决他们的问题；二可以指导督促学生，提高参与的有效性；三可以及时发现典型问题，给课堂添彩.从而使小组合作真正达到相互学习、共同提高的目的.

总之，学生的学习有了动力，他们的思维才会飞翔.而我们教师，就是学生的动力发动机.