理解教材：在整体中思考每节课*

☉江苏省泰州市海陵学校 韩新正

《义务教育数学课程标准（2011年版）》指出，数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构，是实现数学课程目标、实施数学教学的重要资源.［1］章建跃博士说，“从一堂数学课”的角度看，我认为还是“三个理解”，即：理解教材、理解学生、理解教学.所以，正确理解教材是上好一节课的前提.关于理解教材，有人说就是在课标的指导下，认真阅读教材，并对教材进行适当改造，以方便学生接受，就是常说的“用教材教”.显然，在他们看来，“用教材教”就是要改造教材，他们把“教教材”和“用教材教”截然对立起来.其实，教材凝聚着编写者的心血和智慧，他们中许多人也是课程标准的编写者，他们对课标的理解要比普通的教师深刻得多.“教教材”本没有错，关键是要正确理解教材，那么如何准确理解教材呢？笔者认为“把每个章节、每节课放在整体中思考”的做法有助于大家准确地理解教材.下面结合《义务教育教科书·数学》相关内容予以说明，供参考.

一、站在数学本真的高度理解教材

案例1：《义务教育教科书·数学》苏科版七年级上册第1章“数学与我们同行”，共设计了两课时，分别是：“1.1生活 数学”介绍了身份证号码、奥运五环旗、北京奥运会徽等，“1.2活动 思考”安排了折纸剪纸、用火柴棒搭三角形、观察月历等三个活动.显然，本章没有具体的知识点，教师在教学时一般把教材的内容梳理一遍，补充适当的例子，对相关内容做适当的拓展就完成了第一章的教学.然后从第二章开始按照有理数、代数式、方程、函数等顺序安排教学内容.

教材分析：许多老师产生了这样的疑问，第一章安排的目的是什么？如何认识第一章的意义和价值呢？它既没有具体的知识点，又不属于相关章节.数学特级教师卜以楼先生站在全书的高度分析教材，可谓高屋建瓴，值得学习借鉴：不同的学科、不同的年级、不同的主题、不同的教师，可能有不同情怀诉求，但是，助力学生知识生长、生命成长，发挥学科特质、凸显学科内涵、增强学科引擎，让学科知识、方法、思想、素养在第一课中积聚发力，应是共同的价值追求.［2］为此，第一章的核心要义就“不是传授知识，而是传播文化.第一课就应当让学生感受究竟什么是数学，数学的灵魂是什么，数学的价值是什么，数学和其他学科有什么区别；不是盲人摸象，而是整体勾勒.第一课就应当让学生对数学的外貌、结构有一个大致的了解，要对研究数学的基本视角、基本方法有一个结构性的回顾与提升，即要对数学结构性的东西有个基本的把握；不是纪律约束，而是助力生长.第一课教师要选用具有震撼力的教学素材，给学生提供积极思考的载体，让学生体会数学的魅力，以对初中数学产生美好的情愫”.［2］基于这样的认识，我们对第一章的安排就有了全局性的认识.

教学设计：根据上面对第一章的的价值思考，卜以楼先生给出这样的课堂设计，以将教学理念转化为教学行为.本节课共设计三个活动板块.活动1——数学研究的对象.通过举例让学生知道数学是研究“数”和“形”的，并知道“数”和“形”存在于我们的生活中.活动2——学好数学的视角.让学生明白用数学的眼光观察世界——数学抽象，用数学的思维思考生活——数学说理，用数学的语言描述生活——数学符号.活动3——思维活动的方法.分别介绍数学的思维方法——观察、抽象、举例、类比、计算、归纳、说理等.通过这样的教学设计，可以让学生从整体上理解数学是什么，数学学什么，数学怎么学.也许我们不能期望在这一节课中就能解决学生所有的疑问，但是站在回答数学本真的高度来理解教材的安排，可谓匠心独运，值得借鉴.

二、从全章的系统性理解教材

案例2：《义务教育教科书·数学》苏科版八年级上册“2.5等腰三角形的轴对称性（第1课时）”.教材是这样安排的，通过把等腰三角形纸片沿顶角的平分线折叠，引导学生观察，得出等腰三角形的两底角相等和三线合一性质，接着引导学生用不同的方法证明该性质，再引导学生用直尺和圆规作等腰三角形ABC，使得底边BC=a，高AD=h，最后安排例题巩固.

教材分析：这是一节比较难上的课.在一次教学公开课中，一位教师做了这样的设计，既有通过折纸活动发现等腰三角形性质的过程，又训练学生对性质的证明（三种方法）；既使用PPT教学，又规范板书；既有教师讲授，又安排学生合作交流；例题教学既尊重教材，又适当拓展.应该说教师考虑到了教学的所有要素，面面俱到，生怕教学活动不完整，所以整节课下来，课堂密度很大，几无学生思考时间，教师教得匆匆忙忙，学生学得慌慌张张.之所以出现这样的问题，是我们备课时没有真正理解教材，没有把本节课置于全章来思考，故而详略不当，抓不住重点.其实，本章是“轴对称图形”的最后一节，从整章设计来看，思路非常清晰.本章先后设计了轴对称和轴对称图形、轴对称的性质、设计轴对称图案、线段、角的轴对称性、等腰三角形的轴对称性.所以，本章的安排都是基于轴对称来设计的，等腰三角形性质的发现，应该是通过折纸基于实践操作，合情推理即可得出；性质的证明可以引导大家思考折痕的三个属性（顶角的平分线、底边上的高、底边上的中线），然后分类展示；围绕课本例题适当向前铺垫，既巩固所学，又交代出处，再向后拓展，既扩大应用，又锻炼思维，形成一个“知识组块”；证明的规范性可以安排在例题讲解中进行，既节约了时间，又对症施治，这样安排详略得当，张弛有度.

教学设计：我们可以预设这样的教学环节.

【片段1】

师：大家拿出课前做好的等腰三角形纸片（可以是教师做好发给大家），能否对折使图形重合？

生：可以.

师：折叠重合，说明等腰三角形是什么图形？

生：轴对称图形.

师：重合的部分相等吗？可以分成几类来描述？

生：有角相等，等腰三角形的两底角，还有顶角被对称轴分成相等的角；有线段相等，对称轴分底边成相等的线段.

师：怎样把发现用语言表达出来？如何用符号表示这些语言？

……

【片段2】

师：刚才折纸中发现，中间的折痕可以有三种表述方式，请大家试着表述.可以相互交流自己的表述.

生：中间的折痕既是顶角的平分线，也是底边上的中线，还是底边上的高.

师：请分别说说理由.分别按照三种表述来证明等腰三角形的性质，一会儿分别展示.

……

【片段3】

师：已知两条线段a、h，可以作一个等腰三角形吗？

生：可以.若a为底边，以线段a的两端为圆心，h长为半径画弧，两弧的交点就是等腰三角形的顶点.

师：有需要补充的吗？

生：必须满足2h＞a，否则两弧无交点.

师：如果a为底边，h为底边上的高，可以画出这样的等腰三角形吗？

生：可以.等腰三角形底边上的中线、底边上的高合二为一，可以看成底边的垂直平分线.只要画出a的垂直平分线，然后在该线上截取高为h即可.

师：大家可以尝试画一下.

三、从一节课的整体性理解教材

案例3：《义务教育教科书·数学》人教版八年级上册“13.1.2线段的垂直平分线的性质”.教材是这样安排的，先探索垂直平分线的性质，再探索其逆定理，最后安排一个例题.

例已知：直线AB和AB外一点C（如图1）.用直尺和圆规求作：AB的垂线，使它经过点C.

探究作法：

（1）任意取一点K，使点K和点C在AB的两旁；

（2）以点C为圆心，CK长为半径作弧，交AB于点D和E；

作弧，两弧相交于点F；

（4）作直线CF.

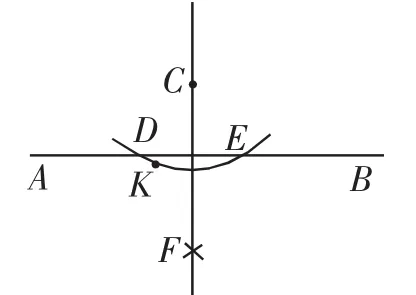
图1

直线CF就是所求作的垂线.

教材分析：这节课的内容比较简单，在进行例题教学时，很多教师一般都是安排学生自学，然后根据画图顺序作出图形，并解释画图的理由，最后变换图形位置作图，巩固所学.很显然，这样的安排学生只是作法的机械执行者，学生只有做完之后才会明白作法，学生自然会发问“你怎么想到的”.同时，本节课的新知和例题之间跨度太大，学生不知其所以然，这样的学习过程缺少深刻而主动的思维活动，而这正是数学课堂的追求，也是教师主导性的具体体现，所以课堂上解决作法的来源才是教学的重点.

由于本节课是线段的垂直平分线的性质，所以我们一定要把例题放在整节课来思考，从线段的垂直平分线来思考如何过直线外一点作已知直线的垂线.我们思考把要作的垂线转化为作某条线段的垂直平分线，关键就是寻找到一条线段，且这条线段的垂直平分线经过点C，于是自然想到在直线AB上寻找这样一条线段，使得该线段的垂直平分线经过点C.课堂上引导学生进行这样的思考正是基于对教材的充分理解.

教学设计：我们预设这样的教学环节.［3］

师：如图2，已知：直线AB和AB外一点C.求作：AB的垂线，使它经过点C.方法不限，请大家自由思考.

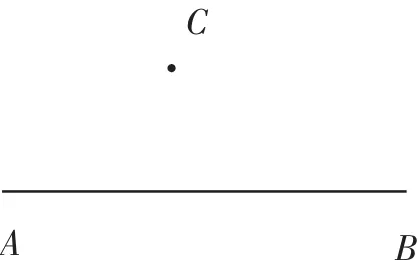
图2

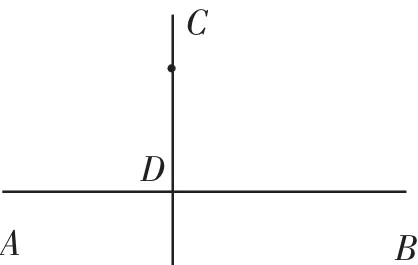
图3

预设：把直线AB对折，使折痕经过点C，折痕所在直线就是AB的垂线；用量角器直接量出∠CDB=90°即可，如图3；使直角三角尺的一条直角边与AB重合，另一条直角边经过点C，过点C的直线即为AB的垂线.

师：如果用尺规作图，该如何思考呢？从上面的三种方法中能否找到可以借鉴的作法？

显然，从上面三种作法中找不到可以借鉴的经验，这时教师的引导显得非常重要.

师：过点C作直线AB的垂线难以下手，结合我们今天所讲的内容（线段垂直平分线），我们是否可以做这样的转化：能否在直线AB上找到一条线段DE，使得线段DE的垂直平分线经过点C？如果找到这样的线段DE，则必有CD=CE，那么如何作出CD=CE呢？（这一步可以留出时间让学生思考、讨论，为什么会想到这样的转化？把未知转化为已知的化归思想是数学的重要思想）

预设：以点C为圆心，以足够长为半径作弧交直线AB于点D、E，如图1.

师：半径有要求吗？

预设：必须保证所画的弧和直线AB有交点.

师：接下来怎么办？

预设：既然已经找到线段DE，下面就是求作DE的垂直平分线了，作法是：分别以点D和点E为圆心，大于DE的长为半径作弧，两弧相交于点F，作直线CF，直线CF就是所求作的垂线.

有了这样的探究过程，学生不仅亲身参与了作图的操作活动，更重要的是思维参与其中.如果本节课反复练习作垂线的各种方法和变式，或许能提高学生的解题熟练程度，而对于学生的思维能力的提高则毫无益处.

教材是学习的载体，要实现数学课程目标就必须充分用好这一载体.理解教材、理解学生、理解教学是我们正确教学的前置功课.姑且不谈高效课堂，就是有效的课堂，我们也应该从这三个方面加强研究.本文给出理解教材的三个策略仅仅是笔者在教学实践中一些做法，很肤浅，期待有更多的同行在理解教材上给出更加切实可行的方法，让我们的教学研究走得更加坚实.