理论指导，实践入手，科学建模——从三角形全等的判定课堂实录说起

☉江苏省海安市城南实验中学 吉雪梅

最近学校组织了一届青年教师大比武活动，为了能够蟾宫折桂，我和我的团队成员在上课前进行了打磨，并进行了“彩排”，再次润色教学过程，最终一炮而红.回顾前面的历练，真是喜忧参半，回味无穷，一些感慨由此流于笔端.

一、与学科组成员的打磨

众所周知，数学起源于生活，并在生活中实践和发展，同时数学可以激发人们的思维能力、启迪人们的智慧.选择什么样的课型，能够充分折射数学的基本思想，提升学生的学科素质呢？是初一年级的代数，还是初二年级的几何，或者是初三年级的复习课？学科组成员的认识是一致的，无论选择哪一个级段，最终传授给学生的一定是一种不折不扣的数学思想.

经过思考，还是选择几何内容，因为此阶段的学生具备了一定的数学知识，只是尚未达到炉火纯青，有利于知识的展开和深化.根据目前的教学进度，授课内容选择了“三角形全等的判断”.

首先，我谈了对教学的三维目标的认识，让学科组成员给予宝贵意见.第一，在知识与技能方面，需要学生抓住“条件”——角边角、角角边，条件是判断三角形全等的命脉，是学生进行思维推理的理论依据.一些成员建议要让学生明确一个三角形有什么要素，能否作为三角形全等的判断条件.这个建议可以吸纳到教学中来.第二是过程与方法，创设情境让学生经历全等三角形条件的探究过程，通过实践获得数学规律.与成员共同商议创设的实践问题的情境，有人建议通过教师在电子白板上画图，然后移动一个三角形与另一个三角形完全重合；有人建议让学生在硬纸板上画图，然后用剪刀裁剪出其中一个三角形，再覆盖另一个三角形.本着以生为本的教学原则，选取了后面的一个建议.第三点是情感态度与价值观，有了前面两点，就可以让学生体验实践过程中的收获，感悟数学规律在生活中的实际意义，从而生成学生的学科思维能力.

其次，分析了学生的学情.本节课建立在学生已有了全等三角形的“边边边”“边角边”知识基础之上.根据前面两节的学习经验，通过电子白板的图形移动或裁剪覆盖得出“角边角（ASA）”或“角角边（AAS）”并非难题，然而如何融于生活、如何启发引导来激发学生的情趣是本课的难点.另一方面，课堂上如何分组讨论、交流，使学生获得探究问题的经验和方法体验，形成实践能力和创新精神是课堂生成的知识重点.

二、课堂“彩排”实录

1.创设导入新课的教学情境

电子白板展示，教师提问学生回答.

（1）在三角形中可以找到的三个元素，包括哪几种情况？（2）你现在可以用哪几种方法判别两三角形全等？生甲：在三角形中可以找到的三个元素有：三条角、三个边、两边一角、两角一边.

生乙：现在可以用三种方法判别两三角形全等，有：①覆盖法（定义）；②边边边法；③边角边法.

师：我们知道，三角形中的三个元素的四种情况：三个角、三条边、两边一角、两角一边，前三种已经探究了，现在继续探究第四种情况“两角一边”能否作为判断两三角形全等的条件.

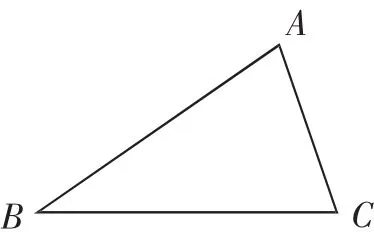
图1

2.课堂活动1

电子白板展示△ABC.

师：△ABC中两角一边有几种可能？

学生自己探究，并展示结果.

电子白板展示：根据三角形的两个内角分别是45°和75°，两角所夹的边为4cm，能在硬纸板上作出一个三角形吗？请其中一个组员将作出的三角形裁剪出来，再与其他学生的进行“覆盖”比较，判断你们所作的三角形是不是全等，由此可以得出怎样的规律？

学生分组并自己动手作图、剪裁，然后与同伴交流，得出结论.

课堂活动展示：各小组将其中一个组员裁剪出来所得三角形进行重叠，发现三角形是完全重合的，说明这些三角形是全等的.

展示规律：两个三角形中的两角和它们的夹边对应相等时全等（简写成“角边角”或“ASA”）.

3.课堂活动2

师：同学们掌握了“角边角”规律后，根据已知的△ABC（如图2），能不能再作一个△A′B′C′，使∠A=∠A′、∠B=∠B′、AB=A′B′呢？（学生思考、举手）请生丙上台演示并说明.

生丙：用量角器量出△ABC中∠A与∠B的度数，再用直尺量出边AB的边长.

如图3，画一线段A′B′，使得A′B′=AB.

分别以A′、B′为顶点，A′B′为一边作∠B′A′D、∠A′B′E，使∠DA′B′=∠CAB，∠EB′A′=∠CBA.

射线A′D与B′E交于一点，记为C′.

即可得到△A′B′C′.

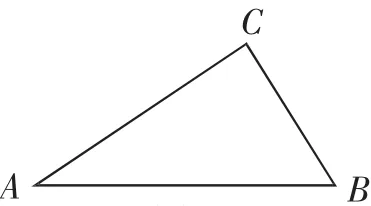
图2

图3

再移动△A′B′C′，与△ABC进行重叠，可以看出两三角形全等.

4.课堂活动3

师：通过生丙的演示可以发现：在两三角形中，若两角和它们的夹边对应相等，则其全等（可以简写成“角边角”或“ASA”）.这也是一个判定三角形全等的条件.想一想，还有判定三角形全等的条件吗？

生丁：因为一个三角形的内角和为180°，若两角一定，则第三个角也一定.是否可以直接用“角边角”推出“两角和其中一角的对边对应相等的两三角形全等”呢？

师：想法很有道理.有没有哪位同学愿意证明他的想法？（学生上台板演）其他学生在下面证明.

学生进行推理证明.（板演过程略）

师：证明过程很到位，请在下面做的学生进行对照，检查自己的方法是否合理.

5.课堂活动4

例已知：如图4，在对边平行的四边形ABCD中，O为四边形的对角线BD的中点，过点O的直线EF分别交AD、BC于E、F两点，连接BE、DF.

求证：△DOE △BOF.师生共析：利用对边平行的四边形的平行线的性质可知夹在两条平行线间的内错角相等.又O为对角线的中点，可以用全等三角形的判定方法得出△DOE △BOF.这是今天学习的新知识.

证明：在对边平行的四边形ABCD中，因为AD∥BC，所以∠ADB=∠CBD.

因为O为四边形对角线BD的中点，所以BO=DO.

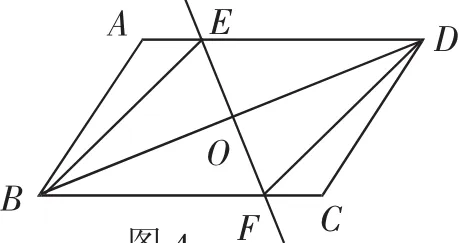
图4

设置目的：本例题主要考查对边平行的四边形中平行线的性质及全等三角形的判定与性质，旨在夯实学生对新知的应用与提高.通过师生共析来明确思路，让学生体验如何向着两个三角形全等的条件靠拢，即找到三个必须的要素，从而培养学生的推理能力.

课堂练习：三道习题（.略）

师：请同学们将三角形全等的判定方法做一个小结，画一个知识框架图.

学生课堂小结：五种判定三角形全等的条件（.具体内容略）

三、课后再次磨合

（1）课堂优点在于采用了学生动手实践的教学方法，能够调动学生的探究激情，让课堂气氛活跃而不沉闷.从选择例题，到习题突破形式，都是深思熟虑的，所选取的例题为中考试题，而且用新学习的全等三角形判断的性质为主题训练方式，显得目标明确，针对性较强.从课堂教学的效果来看，教学设计意图在本节课中算得上水到渠成.

（2）例题典型，师生共同分析思路，再由学生自己写出解题的步骤，使学生思路开阔，增强信心，巩固知识应用.设置了三道课堂练习题，其内容不再赘述.但练习是在已有的基础上，其主要问题的条件、结论都能转化成边、角相等的元素，从而利用五种三角形全等的条件进行推理证明.同时，学生做完本节主要内容之后，进行归纳小结，内化为自己解决问题的方法.

（3）本课也有许多遗憾，如开始以复习的形式导入新课，情境不够轻松.让学生处于思想紧张的状态.可以选用生活中的实例为情境，让学生先在轻松的气氛中探究，建议用一块三角形的玻璃摔碎了，选择哪一块去配制（如图5）.这样，用探究挑逗学生，很容易激起学生求知的欲望.

（4）学生练习时间较短，显得前松后紧，头重脚轻，应压缩课堂活动3，让学生的课堂练习得到充分展示，这样可以避免评价力度不够的现象.

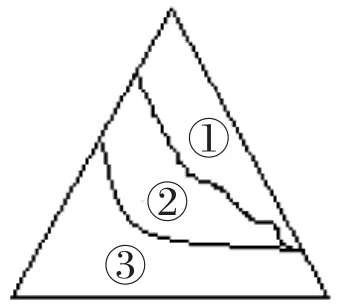
图5

四、写在后面

听取同行的建议，我也在不断反思.这毕竟是在组内的“彩排”，同事的宝贵意见是我走向校级、市级的动力，我深信唯有不断改变自己，才能适应新的教学潮流，才能做中流砥柱.F