一类薛定谔-泊松方程解的存在性

王丽丽，庞翰禹

近年来，众多学者采用变分法来钻研泛函极值问题，并且已经涉猎到了无穷维空间上的非线性泛函问题.临界点理论是变分法的理论基础，它在证明解的存在性以及解的个数时都是最好的理论工具.在钻研薛定谔方程、泊松方程以及薛定谔-泊松方程时，学者们利用临界点理论中的山路引理、喷泉定理以及环绕定理来解决解的存在性问题，不仅取得了丰富的成果，而且其研究也促进了非线性泛函在数学领域的快速发展.

本文主要探究下面的薛定谔-泊松方程

解的存在性,其中3≤p＜5，a与V分别为ℝ3上的连续函数.

迄今为止，诸多学者探究了薛定谔-泊松方程解的存在性，其中比较全面的研究可参考文献［1-7］.余晓辉［1］运用山路引理讨论了薛定谔-泊松方程

至少含有一个非平凡解.Chen H Y和Liu S B［2］假设位势项V满足以下条件：

（V1）V(x)∈C(ℝ3,ℝ),V(x)下方有界，且对于任意M ＞0，都有 μ(V-1(-∞,M])＜∞，其中，μ是ℝ3上的Lebesgue测度.

本文主要是研究带有函数V(x)和变号权a(x)时的薛定谔-泊松方程（1）解的存在性，这也是本文的创新点之一.

1 预备知识

引理1［3］（山路引理）设 E 是Banach空间，I∈C1(E,ℝ)满足

1）I(0)=0 ，存在 ρ ＞0 ，使得 I∂Bρ(0)≥ α ＞0 ；

令Γ是E中联结0与η的道路的集合，即Γ={g∈C[0,1],E)|g(0)=0,g(1)=1}，

定义1（(PS)c序列） 设E是Banach空间，c∈R为给定的实数.若存在序列{un}⊂E，使得I(un)→c，I′(un)→0 ，则称序列{un}是在c水平集的一个(PS)c序列.

定义2（(PS)c条件） 设E是Banach空间，如果对于E中任何点列{un}，只要{I(un)}有界，且 I(un)→0(n→∞)，则{un}必有收敛子列，称I∈C1(E,ℝ)满足（PS）c条件.

定理1 假设以下条件（V）及（a）成立：

（V）V(x)∈C(ℝ3,ℝ),V(x)≥1且对于任意M ＞0，都有 μ(V-1(-∞,M])＜∞ ，其中，μ 是 ℝ3上的Lebesgue测度；

2 主要结果

2.1 泛函结构

由Riesz表示定理知，对于任意固定的u∈H1(ℝ3)，存在唯一的 φu∈D1,2(ℝ3)，使得 φu满足泊松方程-Δφ=u2，则方程（1）便可表示成含有一个变量的方程［8］

于是求解薛定谔-泊松方程（1）等价于求解方程（3），方程（3）的解为对应能量泛函

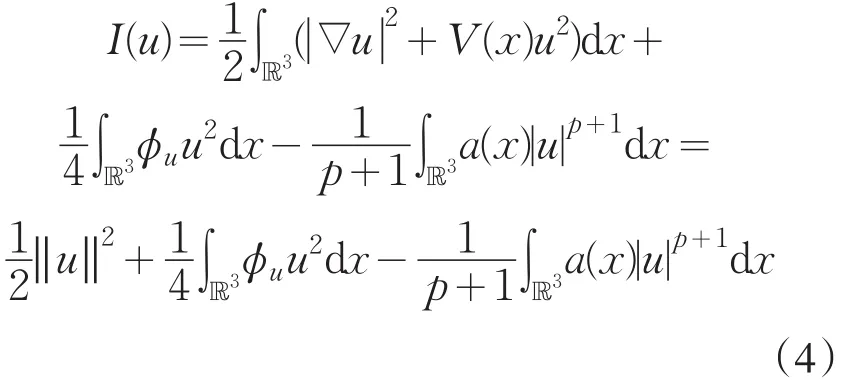
的临界点.

因为 ∀q∈[2,2*]，E连续嵌入到由E连续嵌入到.由 Hölder不等式及C‖u‖4.

引 理 2 定 义 Φ：H1(ℝ3)→D1,2(ℝ3),u→

1）Φ是连续的且Φ是将有界集映射到有界集；

2）若在E中{un}有界且un弱收敛于u,则

证明 1）证明见参考文献［7］中引理2.1.

2） 由 于 φun弱 收 敛 于 φu，则 有

下面往证 ∫ℝ3φun|un-u2|dx→0,n→∞.根据Sobolev不等式及Hölder不等式，有以下不等式成立

又由于

2.2 （PS）c条件

引理3 泛函I满足（PS）c条件

证明 设{un}⊂E是（PS）c序列，则对于c∈R,有 I(un)→c,I′(un)→0(n→∞).

于是有

又因为 I′(un)un=o(1)‖un‖，则

由（5）和（6）得

于是有

又由于

从而有

故 有 ‖un‖→ ‖u ‖ ,即 在E中 有un→u(n→∞).假设un不收敛于u,则‖un‖＜‖u‖.又根 据 条 件此不等式与等式（7）矛盾，所以有un→u(n→∞).

2.3 定理1的证明

下面分两步来找到I(u)的临界点.首先证明存在 ρ＞0,α＞0 ，使得 I(u)≥α 成立，其中∀u∈E,‖u‖=ρ，则从而存在 ρ＞0,使得 I∂Bρ(0)＞α＞0.

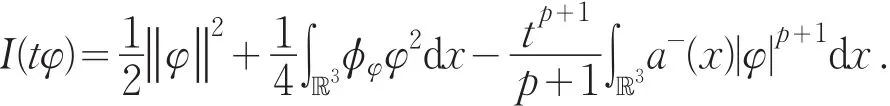
显然存在充分大的t0,使得 I(t0φ)＜0,取η=t0φ,定义 Γ={g∈C[0,1],E)|g(0)=0,g(1)=1}及，由山路引理知，c为 I的一个非平凡的临界点，即式（1）至少存在一个非平凡的解.