圆环上以多项式为符号的Toeplitz算子的亚正规性

尚 巍，关 印，张 楠

关于Bergman空间上的亚正规Toeplitz算子的研究，主要都集中在圆盘上或者单连通区域上.In Sung Hwang和Jongrak Lee给出了圆盘上Bergman空间上Toeplitz算子的亚正规性的必要条件的刻画［1］.Jongrak Lee和Youho Lee给出了圆盘上加权Bergman空间上以多项式为符号的Toeplitz算子亚正规的充分必要条件［2］.Jongrak Lee给出了圆盘上加权Bergman空间上以多项式为符号的块Toeplitz算子亚正规的充分必要条件［3］.C Cowen对Hardy空间上的Toeplitz算子的亚正规性给出了充分必要的刻画［4］.

1 预备知识

记 L∞(Ω)为由关于dA的本性有界可测函数构成的Banach空间，P是从L2(Ω)到(Ω)的正交射影，对任意的z,ω∈Ω，圆环Ω上的再生核定义为为正规化的再生核.则对任意的中 N≥1为某一固定的自然数，0≤i≤N-1，的复数序列.

定义1 设φ∈L∞(Ω )，以φ为符号的Toeplitz算子定义为

以φ为符号的Hankel算子定义为Hφf=(I -P)(φ f )，f∈L(Ω ).其中，I为 L2(Ω)上的恒等算子.

定义2若T为Hilbert空间上的有界线性算子，满足T*T-TT*≥0，则称T为亚正规算子.

命题1 设 f,g为Ω上有界解析函数，则下述条件等价：①Tf+gˉ是亚正规算子.②HHfˉ≥Hgˉ.③ 对 于 任 意 h(z )∈ L2(Ω ) ，有

引理1 设 p，q是整数，则

2）由引理1和本题的1）直接计算可得.

2）类似于引理3的证明.

2 主要结果

定理1设 f(z)=amzm+aNzN,g(z)=a-mzm+a-NzN(0 ＜m＜N ) ，若Tf+gˉ是亚正规算子，则

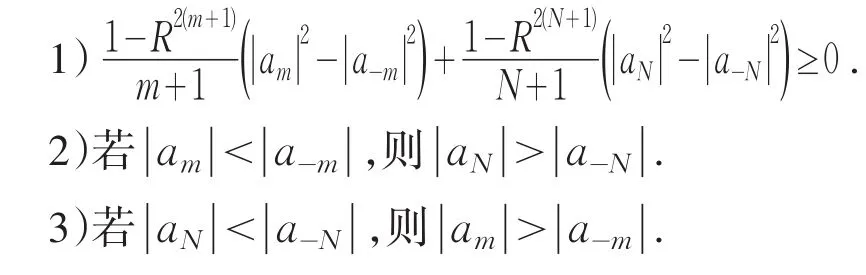
证明 1）若Tf+gˉ为亚正规算子，由命题1中的③可得，当h(z)=1时，有‖f‖≥‖g‖，而

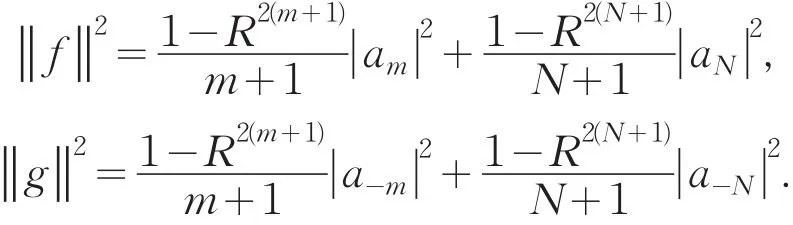
进而1）可得.由1）的结论，2）和3）的结论显然成立.

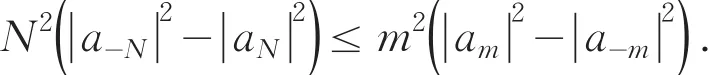
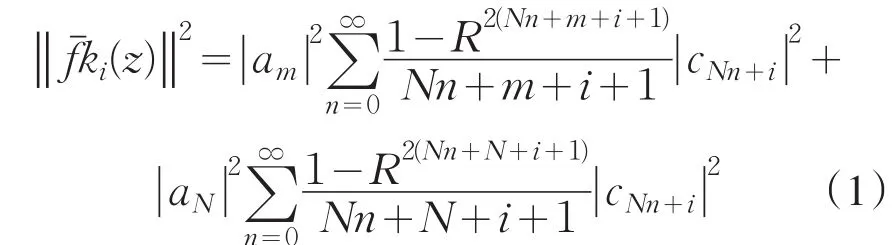
另一方面

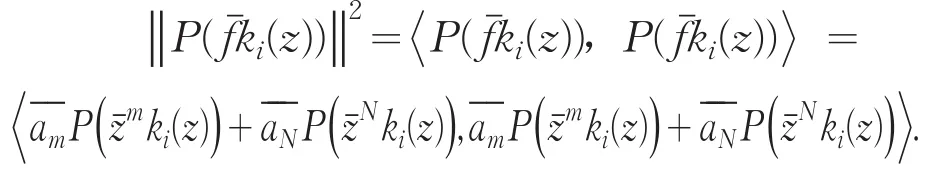
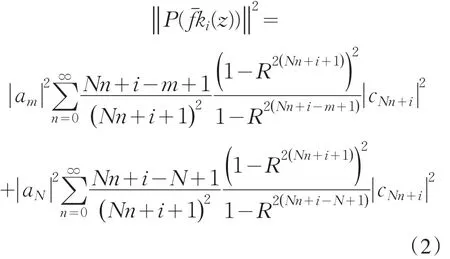
从而，综合（1）式和（2）式，有

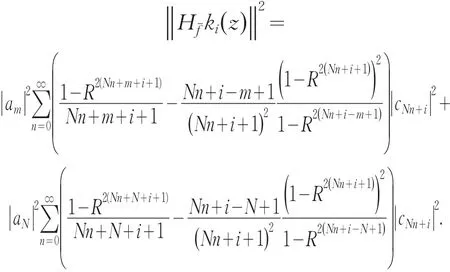
同理可计算

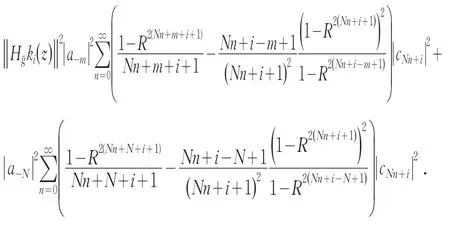
综上

3 结论

本文的研究内容是对前人研究的一个推广，主要体现在3个方面.①可以将Bergman空间推广到其它函数空间，如调和Bergman等函数空间.②考虑将圆环推广到双圆盘或者多连通区域进行研究.③将圆环上Bergman空间上的亚正规Toeplitz算子问题推广到块Toeplitz算子上得出相应结论.