卷曲空间型超表面对声波的调控
2019-01-10许玥蓝君李义丰
许玥,蓝君,李义丰,3
卷曲空间型超表面对声波的调控
许玥1,蓝君2,李义丰1,3
(1. 南京工业大学计算机科学与技术学院,江苏南京 211800;2. 南京大学声学研究所,江苏南京 210093;3. 近代声学教育部重点实验室,南京大学声学研究所,江苏南京 210093)
声学超表面具有天然材料所不具备的独特属性,为声学器件的设计提供了多样性。以广义斯涅尔定律为理论基础,设计了具有多种声波调控能力的折射型相位梯度超表面。该超表面由8个具有不同结构参数的卷曲空间单元结构组合而成,在中心频率3 500 Hz附近,8个单元结构的相位覆盖π范围且声波透射率较高。通过合理地设计超表面水平方向上的相位梯度变化,能够实现对声波的任意调控,在理论和有限元仿真上依次实现了异常折射、无衍射贝塞尔声束和声聚焦。这种厚度薄、透射率高的声超表面,在声学器件设计方面具有潜在的应用价值。
声学超表面;卷曲空间结构;相位梯度
0 引言
近年来,超材料因其独特的物理特性而受到国内外研究学者的广泛关注,它通过在多种物理结构上的设计来突破自然规律对材料性质的限制,从而获得超常的物理性质。声学超材料作为一种新型的人工复合材料,通过在亚波长尺度层次上进行设计和加工,可以实现诸如声隐身[1]、负折射[2]、完美透镜[3]及反向多普勒效应[4]等一系列特殊性能。声学超表面是体积型声学超材料的二维化,具有深度亚波长、超薄、易加工等特点[5]。基于广义斯涅尔定律(generalized Snell’s law)的应用,声学超表面能使声波在波长范围内实现对其参数(振幅、相位等)的调控,进而实现诸如异常折射[6]、体波向表面波转换[7]、声聚焦[8]等波前调控。
广义斯涅尔定律最早在2011年由Capasso课题组提出,并通过设计渐变的V形天线阵列超表面来实现光波相位的梯度变化,打破了传统的折射定律与反射定律[9]。随后Shalaev课题组将这种V形超表面的研究拓展到红外波段,证明该梯度超表面具有宽频特性[10]。从此,各种基于广义斯涅尔定律设计的相位梯度超表面相继被提出,例如T形结构[11]、H形金属结构[12]、矩形纳米棒[13]以及C型结构[14]等各种结构的超表面。这些二维阵列的相位梯度超表面能够任意调控电磁波的传播方向,进而实现负折射、深聚焦和波束偏转等奇特的物理现象[15-16]。
在声学中同样可以引入相位梯度超表面的概念,其基于广义斯涅尔定律的应用,通过调节超表面横向的声速梯度或折射率梯度,可以灵活地调控反射或折射波前。对于横向声速梯度变化的超表面,2015年Tian等[17]通过设计一系列声速不同但阻抗与背景介质匹配的五模单元用以构造梯度超表面,并且高效地实现了异常折射、贝塞尔波束、声聚焦等声波波前调控。但是这类超表面对单元的结构有比较高的要求,且分布相对比较复杂。除了五模单元结构,赫姆霍兹共鸣器也可以用于实现声速梯度变化的超表面[18]。对于另外一种方法,通过改变横向折射率梯度而构造的超表面[19],目前最常用的方法主要是通过卷曲空间型结构来实现,这种设计使声波沿着卷曲路径传播,因此在经过亚波长单元结构后,声波的传播路径被延长,进而使单元结构的相对折射率增大且可以产生高达2π范围的相位变化。2012年Liang等[20]首次提出基于迷宫型单元结构而构成的卷曲空间型超表面,通过控制声波传输通道的总长度,可以方便地调控声波的相位、有效参数和色散关系。之后,Li等[21]将其简化为单层的卷曲空间型声学超表面,实现了2π范围的相位覆盖区域,实现了声聚焦、异常反射等声波波前调控。2015年Yuan等[22]通过实验证明了该类卷曲空间型声学超表面能够生成理想的梯度相移的二次声源,从而实现声辐射模式的转换。相比其他结构的超表面,卷曲空间型超表面具有深度亚波长尺度,耦合效率高、结构简单、易构造等特点。
本文利用卷曲空间结构设计了一种具有高透射效率的亚波长声超表面,实现了对透射声波相位在0~π范围内的任意调控。本设计中卷曲空间单元的相位变化主要通过调节单元结构内部的结构参数来实现。基于广义斯涅尔定律,设计了一系列相位分布不同的卷曲空间单元,并将这些单元进行不同的组合构成不同的超表面,进而实现异常折射、贝塞尔声束、声聚焦等波前调控。
1 结构设计及机理分析
1.1 卷曲空间型单元结构设计
本文利用卷曲空间型结构来构造亚波长声学超表面,设计了相位从0~π范围内按照梯度变化的8个超表面单元结构。根据广义斯涅尔定律,将这8个单元结构在水平方向上合理地排列,从而实现对声波的引导和调控。图1是本文设计的卷曲空间型单元结构示意图。该单元结构由上下两个齿状结构拼接而成,将其放置于空气中,空气的密度和声速分别为1.21 kg·m-3和343 m·s-1。图1中参数和分别为超表面单元结构的长和宽,是齿条的长,是齿条的宽,是单元结构形成空气通道的宽度。本文将单元结构参数设置为=10.69 mm,=10 mm,=0.67 mm,=1 mm。由于声波是标量波,不存在截止频率,因此声波可以自由地在弯曲的空气通道中传播。相比较声波在自由空间中由入口到出口两点简单的直线传播,卷曲的空间结构使得声波的传播路径延长,故声波的相位在很大程度上被延迟[23]。因此,我们可以通过调整卷曲空间结构的齿条长度来改变声波传播路径的长度,从而使声波经过不同的单元结构后相位得到不同程度的延迟,由此获得相位梯度变化的超表面。除此之外,还可以通过增加齿条数目以及超表面的长度来延长声波在单元结构中的传播路径,但这会使超表面的厚度增加的同时降低了声波的透射率。另外,通过调节齿条宽度或空气通道的宽度虽然也能够改变声波在单元结构中传播的总路径,但其对声波相位变化影响较小。因此,本文采用在单元结构外形尺寸保持不变的情况下调整内部齿条长度的方式来获得相位可调的声学超表面,其在实际应用中具有重要的意义。
1.2 卷曲空间型单元结构的机理分析
在光学领域,人们利用等离激元[13]的共振效应实现了光学的超表面,并由此产生了一系列特殊光学现象。而在卷曲空间型结构的声学超表面中,声波沿着弯折的通道传播,相比较简单的直线传播而言,其传播总路径增长,因此声波的相位会发生相应的延迟,从而实现超常的声学物理特性。为了设计高透射率的声学超表面,应尽可能地保证超表面的声阻抗与背景介质匹配。直观上从图1中可以发现,卷曲空间型单元结构的入口和出口都比较狭小,因此存在较高的相对等效阻抗,从而导致声阻抗的不匹配。但是对于一些特殊的频率,该结构的相对等效阻抗可以与空气的阻抗有效匹配。为了验证理论分析的正确性,我们对如图1所示的单元结构进行有限元仿真,将该单元结构放置于空气中,平面波从其左侧垂直入射。利用有限元仿真软件COMSOL MULTIPHYSICS 计算出单元结构右侧的透射波声强以及左侧入射波声强,通过计算透射波声强与入射波声强之比得到其声能量传输因数,该传输因数随频率变化的曲线如图2所示。从图中可以看出,在工作频率=3 500 Hz附近,单元结构具有较高的传输因数,声波能够高效地传输。此时,波长与单元结构尺寸的比为=9.2,即工作波长远大于单元尺寸,这有利于声学器件的集成。在本文提出的声学超表面中所有的单元结构外部尺寸相同,我们仅通过改变齿条的长度来调控每个单元结构的相位变化。共设计了8个卷曲空间型单元结构,使得在3 500 Hz频率附近实现相位从0到π范围内的调控,其齿条长度分别从7.34 mm递减至5.8 mm。图3中空心圆点显示了这8个单元结构对应的相位,从图3中可以看出相邻2个单元结构的相位差为π/7。为了进一步验证这8个单元结构的离散相位,我们计算了8个单元结构透射声波的声压场分布,如图4所示,从图4中可以看出,透射波声压场发生了半个波长的变化,充分地证明了该组合结构实现了相位从0到π范围内的调控。之后利用广义斯涅尔定律,通过选择合适的单元排列方式,便可实现对透射波的波阵面进行任意调控,如异常折射、无衍射贝塞尔声束和声聚焦。

图1 声学超表面单元结构示意图
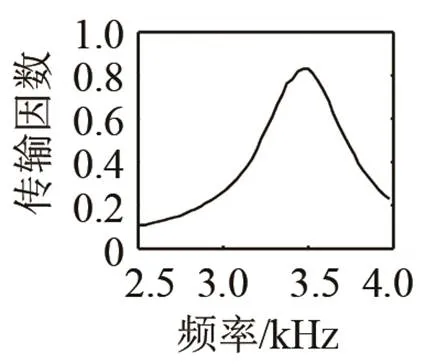
图2 声学超表面能量透射谱
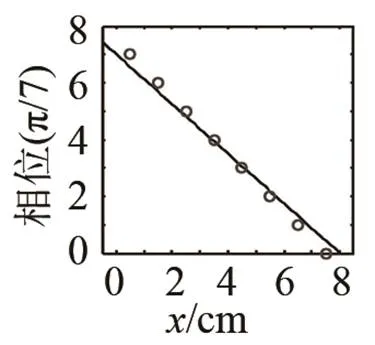
图3 不同齿条长度的8个单 元结构的相位分布

图4 透射声波的声压场分布
2 声学超表面的声波调控
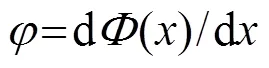

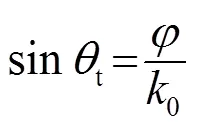
2.1 异常折射
由式(1)、(2)可知,相位梯度变化的超表面能够调节声波的传播方向,因此通过合理地设计基于卷曲空间型结构的超表面能够实现声波的异常折射,其声波转换示意图如图5所示。入射波沿着+方向垂直入射到超表面,透过超表面后发生偏折。当已知超表面的相位梯度时,利用上述广义斯涅尔定律,可以计算声波透过该超表面后产生异常折射的折射角,即

当入射角时,折射角关于相位梯度变化的情况如图6所示。图中黑色实线是理想情况下超表面产生异常折射的角度随相位梯度变化的分布情况,结果表明理想情况下相位梯度越大,发生异常折射的折射角也越大。空心圆点是实际选取不同相位梯度的超表面进行数值仿真的情况,从图中可以看出,空心圆点都落在了黑色实线上,说明数值仿真结果与理论推导结果相吻合。为了进一步验证理论分析的合理性,我们选取了其中的两种不同相位梯度变化的超表面。当相位梯度时,该超表面由16个单元结构组成,每两个相同的卷曲空间型单元结构按相位变化程度在水平方向周期性排列,将相位变化最大的单元结构放置在超表面的最左边,相位变化最小的单元结构放置在超表面的最右边,即,,D是该超表面的宽度。由式(3)理论分析可得其对应的折射角为17.8°。在工作频率为3 500 Hz时,声波透过该超表面后的声压分布的数值仿真结果如图7所示。图7中黑色箭头为理论分析的异常折射角度,从图中可以看出,当垂直入射的平面波透过超表面后,透射波前偏离了原有的传播方向,数值仿真结果中透射波的偏折角度与理论分析基本一致。图8是时的声压分布图,该超表面共有32个单元结构组成,每4个相同的卷曲空间型单元结构按相位梯度变化在水平方向周期性排列。理论分析可得其对应的折射角为8.8°,同样得到数值仿真结果中透射波的偏折角度与理论分析是一致的。理论和仿真结果都充分地表明,当声波沿着+y方向垂直入射到超表面时,通过改变超表面的相位梯度变化可以实现声波沿角度偏折的异常折射。

图6 折射角与相位梯度变化的关系图

图7 当时, 超表面的声压场分布图
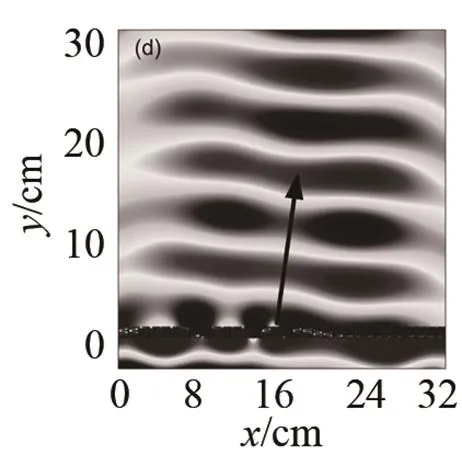
图8 当时, 超表面的声压场分布图
2.2 无衍射贝塞尔声束
贝塞尔声束可以由两束传播角度相反的平面声波叠加而成,重叠的区域即为贝塞尔声束形成区域[25],对应产生无衍射贝塞尔声束的原理示意图如图9所示。入射波沿着+方向垂直入射到超表面,透过该超表面后形成两束角度分别为和的平面波,叠加产生无衍射的贝塞尔声束。基于广义斯涅尔定律,沿着方向超表面的相位分布应满足
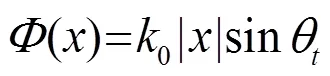
其中,是贝塞尔声束的基角,在本文中将其设置为13.5°。由式(4)可得,理想情况下超表面连续的相位沿水平方向的分布如图10中虚线所示,实际设计超表面的相位梯度分布情况如图10中实线所示,相位分布关于x轴对称。根据理论分析设计的超表面共有45个卷曲空间型单元结构组成,将相位变化最小的单元结构放置在超表面的中间,相位最大的放置在超表面的两边,即,,D是该超表面的宽度。与超表面产生异常折射的情况相比,形成无衍射贝塞尔声束的超表面实际上就是将第1节提出的超表面结构关于中心处对称分布。图11是在3 500 Hz时,声波透过该超表面后声强分布的数值计算结果,平面波透过超表面后形成无衍射贝塞尔声束并且其沿着+y方向上有相对较长的距离传播,其中用黑色实线框出的菱形区域即为贝塞尔声束形成区域。仿真结果与图9中理论分析完美匹配,表明相位梯度声学超表面可以产生等效的无衍射贝塞尔声束。

图10 相应于图9的沿x方向 超表面相位分布图

图11 无衍射贝塞尔声束的声强分布图
2.3 亚波长平面声聚焦
利用卷曲空间型声学超表面设计亚波长声学平面透镜,平面波垂直入射到声学超表面产生声聚焦现象的原理示意图如图12所示。本文假设声能量聚焦点的坐标为,声学超表面相位变化呈典型的双曲线分布,对于给定的焦距,沿着轴的相位应满足

其中,假设焦距。图13中虚线即为满足式(5)的理想情况下超表面相位沿x的连续分布情况,实际设计的声学平面透镜的相位梯度变化为图13中实线所示。通过相位分布图可以很容易地构造出实现声聚焦的超表面,该超表面由36个单元结构排列组成。通过数值仿真得到,当声波频率f = 3 500 Hz时,平面波透过该声学超表面后声强空间分布的数值计算结果如图14所示,从图中我们可以发现,平面波透过该超表面后在点(0,29)附近具有明显的声聚焦现象,并且透射能量集中点的坐标与理论设定值相一致。为了进一步证明本文设计的超表面能够获得完美的声学聚焦,我们求解了焦点所在直线y=y0上的声强分布图,结果如图15中黑色实线所示,其即为图14中焦点处沿垂直于y轴方向的声强分布,入射声强如图中黑色虚线所示。从图中归一化处理后的结果可知,焦点处的声强是入射声强的2.8倍,这说明该超构表面具有高效的声能量聚焦功能。
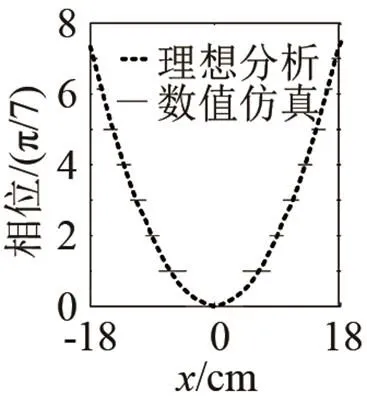
图13 相应于图12的沿x方向超表面相位分布图

图14 声学聚焦原理示意图

图15 声学聚焦超表面的声强 分布图
根据互易原理,声学超表面除了能实现声聚焦外,还能够实现声聚焦的逆过程,即可以将柱面波有效地转换为平面波。图16为波形转换的原理示意图,由点源激发形成的柱面波从超表面左侧入射,右侧透射波为平面波。根据上述声聚焦的分析,点源的坐标为(0,-29)与聚焦点的坐标关于超表面对称。图17是声波频率=3 500 Hz时柱面波转换为平面波的声压分布数值仿真图,从图中可以看出,该超表面能够将柱面波转换为平面波。
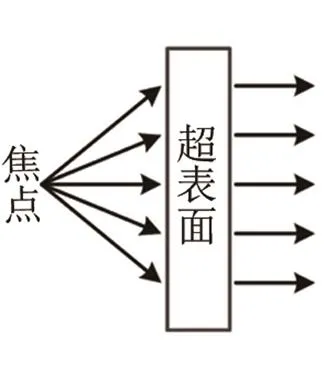
图16 柱面波转化为平面波原理示意图

图17 柱面波转化为平面波声压分 布图
3 结论
本文利用卷曲空间结构设计了折射型相位梯度超表面,通过调节单元结构的齿条长度可以实现在0到π范围的相位调控。基于广义斯涅耳定律,通过合理地排列单元结构从而设计出不同相位梯度变化的超表面,能够实现对声波的任意调控。在有限元仿真中用不同相位梯度变化的声学超表面调控声波,实现了声异常折射、无衍射贝塞尔声束以及声聚焦,验证了设计结构及设计方法的有效性。数值计算结果表明,该声学超表面不仅具有深度亚波长结构,还表现出较高的传输效率。这种厚度薄、传输效率高、具有极好的波前调控能力的声学超表面,在实现声学器件的小型化方面具有潜在的应用价值。
[1] CUMMER S A, SCHURIG D. One path to acoustic cloaking[J]. New Journal of Physics, 2007, 9(3): 45.
[2] LIU J, HOU Z L, FU X J. Negative refraction realized by band folding effect in resonator-based acoustic metamaterials[J]. Physics Letters A, 2015, 379(36): 2097-2101.
[3] KAINA N, LEMOULT F, FINK M, et al. Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials[J]. Nature, 2015, 525(7567): 77-81.
[4] ZHAI S L, ZHAO X P, LIU S, et al. Inverse doppler effects in broadband acoustic metamaterials[J]. Scientific Reports, 2016, 6(1): 32388.
[5] SHEN C, JING Y. Acoustic metasurfaces for asymmetric transmission[J]. J. Acoust. Soc. Am., 2015, 138(3): 1735.
[6] TANG K, QIU C, KE M, et al. Anomalous refraction of airborne sound through ultrathin metasurfaces[J]. Scientific Reports, 2015, 4(1): 6517.
[7] LI Y, LIANG B, GU Z M, et al. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces[J]. Scientific Reports, 2013, 3(7464): 2546.
[8] ZHU Y F, FAN X, LIANG B, et al. Multi-frequency acoustic metasurface for extraordinary reflection and sound focusing[J]. AIP Advances, 2016, 6(12): 121702.
[9] YU N, GENEVET P, KATS M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction[J]. Science, 2011, 334(6054): 333-337.
[10] NI X J, EMANI N K, KILDISHEV A V, et al. Broadband light bending with plasmonic nanoantennas[J]. Science, 2012, 335 (6067): 427.
[11] PU M B, CHEN P, WANG C T, et al. Broadband anomalous reflection based on gradient low-Q meta-surface[J]. AIP Advances, 2013, 3(5): 52136.
[12] SUN S L, HE Q, XIAO S Y, et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves[J]. Nature Materials, 2012, 11(5): 426-431.
[13] SAEIDI C, WEIDE D V D. Wideband plasmonic focusing metasurfaces[J]. Applied Physics Letters, 2014, 105(5): 53107.
[14] DING C L, ZHOU Y W, ZHAO X P, et al. The anomalous reflection of acoustic waves based on metasurface[J], 2015, 2216(1): 755-758.
[15] 郭文龙, 王光明, 李海鹏, 等. 单层超薄高效圆极化超表面透镜[J]. 物理学报, 2016, 65(7): 74101.
GUO Wenlong, WANG Guangming, LI Haipeng, et al. Utra-thin single-layered high-efficiency focusing metasurface lens[J]. Acta Physica Sinica, 2016, 65(7): 74101.
[16] 刘晓波, 施宏宇, 陈博, 等. 折射率梯度表面机理的研究[J]. 物理学报, 2014, 63(21): 120-125.
LIU Xiaobo, SHI Hongyu, CHEN Bo, et al. Studies on the mechanism of refractive index gradient surface[J]. Acta Physica Sinica, 2014, 63(21): 120-125.
[17] TIAN Y, WEI Q, CHENG Y, et al. Broadband manipulation of acoustic wavefronts by pentamode metasurface[J]. Applied Physics Letters, 2015, 107(22): 221906.
[18] LAN J, LI Y F, XU Y, et al. Manipulation of acoustic wavefront by gradient metasurface based on Helmholtz Resonators[J]. Scientific Reports, 2017, 7(1): 10587.
[19] ZIGONEANU L, POPA B, CUMMER S A. Design and measurements of a broadband two-dimensional acoustic lens[J]. Physical Review B, 2011, 84(2): 24305.
[20] LIANG Z X, LI J S. Extreme acoustic metamaterial by coiling up space[J]. Physical Review Letters, 2012, 108(11): 114301.
[21] LIANG Z X, FENG T H, LOK S, et al. Space-coiling metamaterials with double negativity and conical dispersion[J]. Scientific Reports, 2012, 3(4): 1614.
[22] LI Y, LIANG B, ZOU X Y, et al. Extraordinary acoustic transmission through ultrathin acoustic metamaterials by coiling up space[J]. Applied Physics Letters, 2013, 103(6): 63509.
[23] YUAN B, CHENG Y, LIU X J. Conversion of sound radiation pattern via gradient acoustic metasurface with space-coiling structure[J]. Applied Physics Express, 2015, 8(2): 27301.
[24] LI Y, LIANG B, TAO X, et al. Acoustic focusing by coiling up space [J]. Applied Physics Letters, 2012, 101(23): 233508-233512.
[25] PADGETT M, BOWMAN R. Tweezers with a twist[J]. Nature Photonics, 2011, 5(6): 343-348.
[26] DURNIN J. Exact solutions for nondiffracting beams. I. The scalar theory[J]. Journal of the Optical Society of America. A, 1987, 4(4): 651-654.
Acoustic wave regulation and control by coiling up space typed metasurface
XU Yue1,LAN Jun2, LI Yi-feng1,3
(1. College of Computer Science and Technology, Nanjing Tech University, Nanjing 211800, Jiangsu, China; 2. Institute of Acoustics, Nanjing University, Nanjing 210093, Jiangsu, China; 3. Key Laboratory of Modern Acoustics, Ministry of Education, Nanjing University, Nanjing 210093, Jiangsu, China)
The acoustic metasurface has unique properties which are not possessed by natural materials, it provides diversity for the design of acoustic devices. In this paper, it is theoretically demonstrated that the generalized Snell’s law can be used for designing acoustic gradient metasurface to achieve acoustic wavefront regulation and control. The metasurfaces are constructed by eight coiling up space units of a solid structure having different structural parameters. The eight units can provide discrete phase shifts covering π span and have the extraordinary acoustic transmission coefficient around the frequency of 3 500 Hz. Arbitrary regulation and control of acoustic wavefront can be achieved by appropriately designing the phase gradient profiles in the transverse direction of the metasurface. The theoretical and numerical results show that some excellent wavefront regulations, such as anomalous refraction, non-diffracting Bessel beam and sub-wavelength flat focusing, can be achieved. The ultrathin metasurfaces with high transmission coefficient has potential application in acoustic devices.
acoustic metasurface; coiling up space; phase gradient
O422
A
1000-3630(2018)-06-0515-06
10.16300/j.cnki.1000-3630.2018.06.001
2017-11-03;
2017-12-07
国家自然科学基金(615741222)、江苏省六大人才高峰高层次人才项目。
许玥(1993-), 女, 江苏南京人, 硕士研究生, 研究方向为声学人工材料。
李义丰,E-mail: lyffz4637@163.com
