Fe-Ga合金发音振子换能器的多场耦合模型

翁玲，李薇娜，梁淑智，徐行



Fe-Ga合金发音振子换能器的多场耦合模型

翁玲，李薇娜，梁淑智，徐行

(河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130)

建立了Fe-Ga合金弓张结构发音振子换能器电场、磁场和固体力学场的多场耦合模型，研究了发音振子换能器磁场强度、磁感应强度和应变分布情况，并进行了换能器在不同频率下的磁场强度分析和模态分析。分析发现，随着频率的增高，Fe-Ga合金发音振子换能器的磁场强度逐渐减小，计算得到换能器的共振频率为984 Hz。测试了Fe-Ga合金换能器中的核心元件Fe-Ga合金的磁场强度与应变的关系，当磁场强度饱和值为40 kA·m-1时，应变为70×10-6。搭建了磁致伸缩材料磁特性测试系统，测试了Fe-Ga合金磁场频率为5、20、50 Hz的磁滞曲线，并测试了Fe-Ga合金的应变随频率的变化曲线，实验结果与换能器中Fe-Ga合金的应变仿真结果一致。

Fe-Ga合金；模态分析；多场耦合模型；发音振子换能器

0 引言

磁致伸缩材料是一种具有磁致伸缩效应的智能材料[1]。Terfenol-D材料具有较高的居里温度、较低的磁晶各向异性和较大的磁致伸缩性[2]。但是它的机械性能差，使它承受冲击载荷或者是拉应力的能力变差。Fe-Ga合金是在Terfenol-D[3]后美国海军表面武器研究室研制的另一种新型超磁致伸缩材料。Fe-Ga合金材料有正效应和逆效应，具有应变较大、响应时间短、磁滞小等优点[4]，是新型致动器[5]、传感器[6]、振动发电机[7]等各种超磁致伸缩换能器件的优选材料。人们通过两种方式可以听到声音[8]，一种是气导方式，一种是骨导方式。骨导技术是新兴发展起来的听觉技术，可以更好地提供给人们更高的听觉质量，并解决了传统的气导耳机在嘈杂的环境、水下等特殊的环境不能使用的问题[9]。电磁式和压电式骨导耳机现在已发展成熟，电磁式骨导耳机工作性能较好，但是功率大，难以实现微型化。曾平等[10]提出的压电骨传导听觉装置不会受到外界磁场的干扰，它比电磁式的应用领域更为广泛。但是由于压电材料的谐振频率较高，低频衰减大，导致声音失真。超磁致伸缩材料与压电材料相比，具有谐振频率低的特点，因此更适合用于骨导技术[11-12]。赵正龙等[13]提出利用Terfenol-D材料弓张结构的发音振子换能器，可以有效弥补压电材料低频响应不足的缺陷，但是机械性能差，导致传音效果较差。

本研究提出以Fe-Ga合金为核心部件制成弓张结构发音振子换能器，可用在公安、消防和部队通讯等领域。通过Terfenol-D与Fe-Ga合金分别应用于发音振子换能器上，得到了发音振子换能器电场、磁场和固体力学场多场耦合模型，研究了发音振子换能器磁场强度、磁感应强度和应变分布情况，并进行了换能器在不同频率下的磁场强度分析和模态分析。同时，利用Fe-Ga合金棒磁致伸缩特性测试系统对Fe-Ga合金棒的静态应变曲线进行测量。利用磁致伸缩材料磁特性测试系统，测试了Fe-Ga合金在磁场频率为5～50 Hz时的曲线，与计算出的多场耦合模型计算结果进行了对比。测试了Fe-Ga合金的应变随频率的变化曲线，与多场耦合模型的计算结果进行了比较。

1 发音振子换能器的结构与工作原理描述

发音振子换能器的结构如图1所示。发音振子换能器由超磁致伸缩棒(Terfenol-D和Fe-Ga合金)、永磁体、螺钉、线圈、散热层和弓张结构组成。超磁致伸缩棒在外加磁场的作用下，会产生应变。在棒的外层绕有线圈，线圈可以提供驱动磁场。在棒的两端是永磁铁，用来提供偏置磁场。发音振子换能器的顶端是螺钉，螺钉起的作用是固定及施加预应力。线圈的外层绕有散热层，起到散发热量的作用。弓张结构用来固定及传递振动。

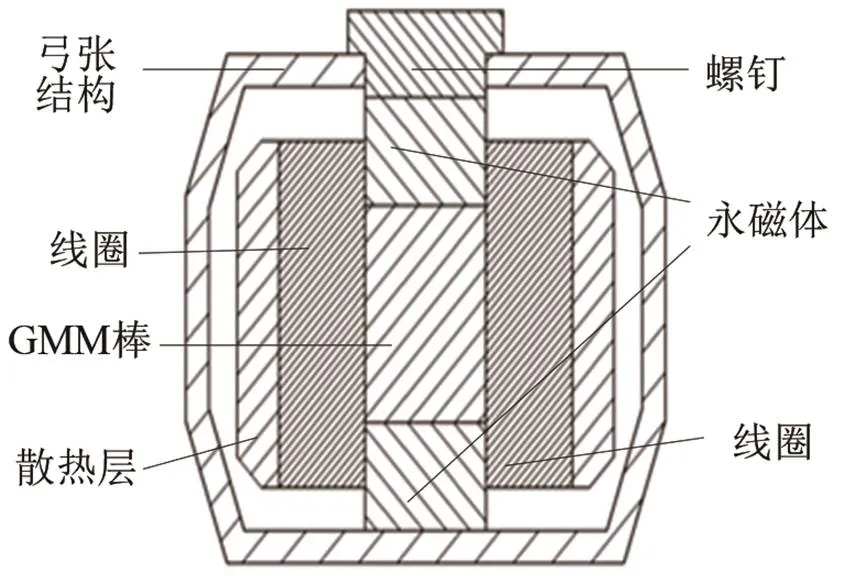
图1 发音振子换能器结构图

弓张结构发音振子换能器的工作原理是：当线圈通有电流，线圈会产生驱动磁场。在线圈提供的驱动磁场和永磁体提供的偏置磁场共同作用下，使得超磁致伸缩棒会产生磁致伸缩形变，从而能够使弓张结构发生形变，弓张结构将振动信号通过颅骨传递给内耳，最终人们能够听到声音。

2 发音振子换能器分析建模

2.1 多物理场耦合模型

2.1.1 磁致伸缩模型

空间中的磁场强度和磁感应强度之间的关系为[14]

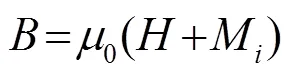
由式(1)可得：

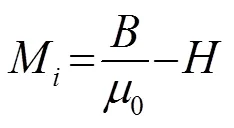
磁致伸缩棒沿任意方向的磁致伸缩应变与磁化强度的关系可以用能量的二次畴转模型表示：

2.1.2 非线性压磁模型

描述磁致伸缩量和应变的非线性压磁方程为

由式(4)和式(5)联立可得：

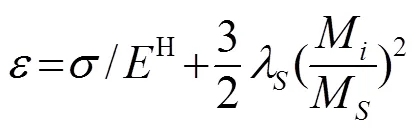
将式(2)与式(6)联立可得：

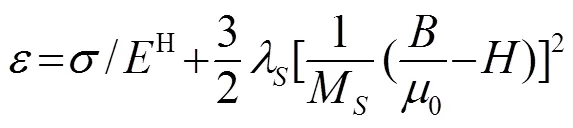
式(7)为磁致伸缩棒的电场、磁场和固体力学场耦合模型。

2.2 有限元模型

利用二维有限元方法对发音振子换能器进行建模，分别将Terfenol-D和Fe-Ga合金材料的参数输入到模型中。各部分的材料属性如表1所示。

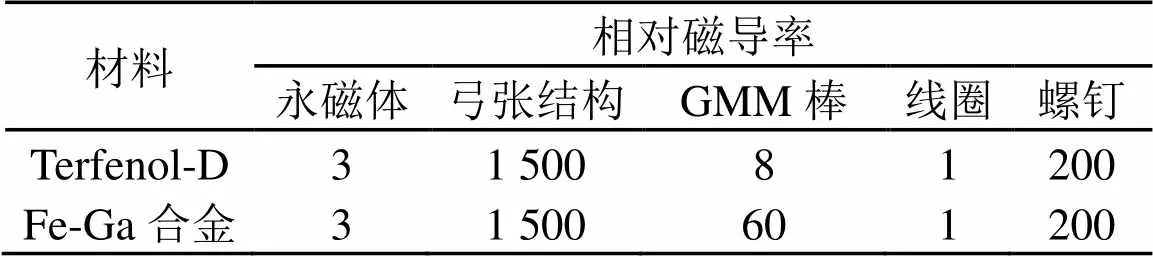
表1 材料的参数说明

COMSOL有限元网格的划分至关重要，它直接影响着模型计算结果的正确性。为了使发音振子换能器磁路部分的计算更加精确，组成磁路的两个永磁体、磁致伸缩棒、螺钉和弓结构的划分要更为精细。划分结果如图2(a)所示。图2(b)是发音振子换能器的磁力线的分布图，可以看出，两个永磁体，磁致伸缩棒、螺钉和弓张结构形成闭合磁路，最大限度地减少了漏磁。

图2 模型结构图

3 发音振子换能器驱动响应及谐振特性仿真分析

3.1 发音振子换能器的动态分析

发音振子换能器工作在交流状态，输入的交流电流值为5 A，频率为50 Hz，线圈的匝数为224匝。

发音振子换能器中磁致伸缩棒的磁场分布如图3所示，横坐标为磁致伸缩棒的轴线，横坐标的零刻度处是棒的底端，纵坐标为磁场强度值。取磁致伸缩棒的中心轴线的磁场强度进行分析。基于模型计算得：Fe-Ga合金棒的2～8 mm处的磁场强度可达7 kA·m-1，Terfenol-D棒的2～8 mm处的磁场强度波动较大。并且Fe-Ga合金棒中间段4～8 mm处的磁场较均匀，波动不大，有利于发音振子换能器更好地工作。

发音振子换能器中磁致伸缩棒的磁感应强度沿直径方向的分布如图4所示，横坐标为沿磁致伸缩棒的直径方向的距离，刻度2 mm处为圆心，纵坐标为磁感应强度值。通过两条曲线的对比可得：Fe-Ga合金材料的磁感应强度较大，最大能达到0.6 T，Terfenol-D材料的磁感应强度最大能达到0.25 T。并且Fe-Ga合金材料的磁感应强度均匀，波动小，有利于发音振子换能器高效平稳地工作。

图3 换能器中磁致伸缩棒沿中心轴线的磁场分布

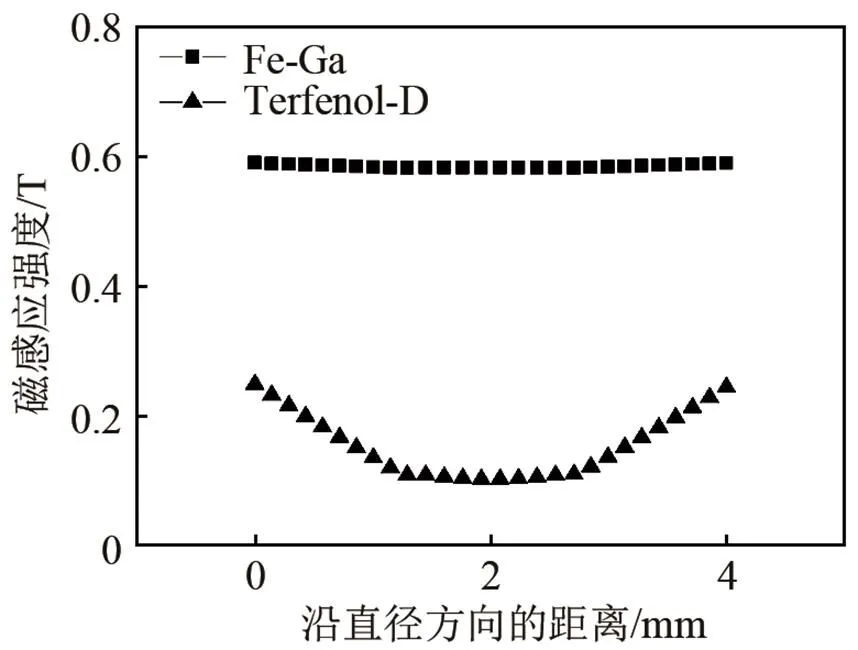
图4 换能器中磁致伸缩棒沿直径方向的磁感应强度分布

发音振子换能器中磁致伸缩棒的应变沿直径方向的分布如图5所示，横坐标为沿磁致伸缩棒直径方向的距离，刻度2 mm处为圆心，纵坐标为应变值。通过两条曲线的对比可得：Fe-Ga合金棒的边缘应变可以达到78×10-6，Terfenol-D棒的边缘应变达到160×10-6。Fe-Ga合金棒中心点向外1 mm 外1 mm处的应变为40×10-6。虽然Terfenol-D棒的处的应变均匀为10×10-6，Terfenol-D棒的中心点向应变值大，但是其抗拉强度差，不利于发音振子换能器的振动传递。

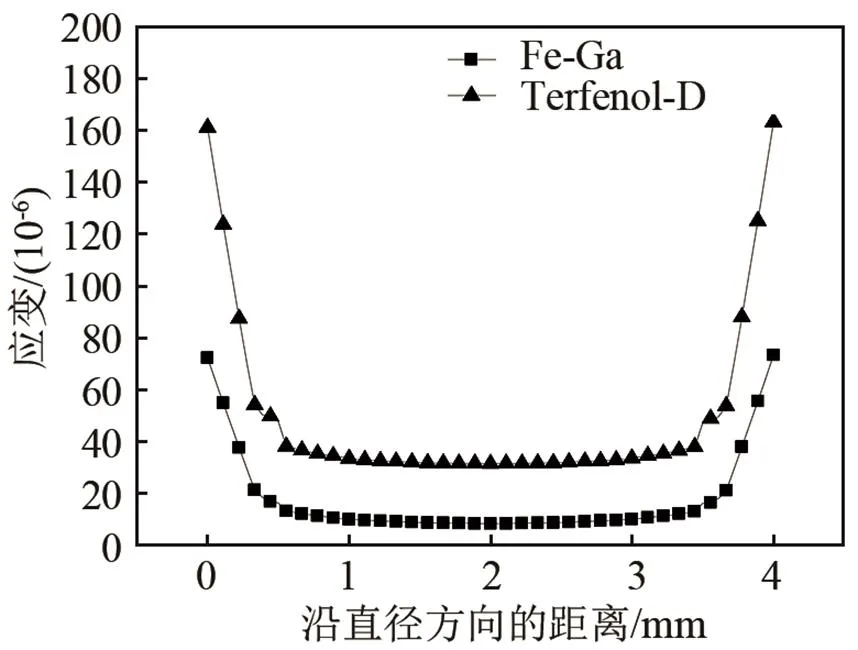
图5 换能器中磁致伸缩棒沿直径方向的应变分布

Fe-Ga合金在磁场频率为1、200、500、1 000、1 400、2 000 Hz下的磁场分布如图6所示。在Fe-Ga合金中心点(=0 mm)的磁场强度分别10.9、10.8、9.5、7.9、6.8、5.5 kA·m-1。骨传导听觉敏感区的工作频率一般在1～2 000 Hz，当频率较高时，由于磁滞效果加强，所以中心点的磁场强度逐渐减小。

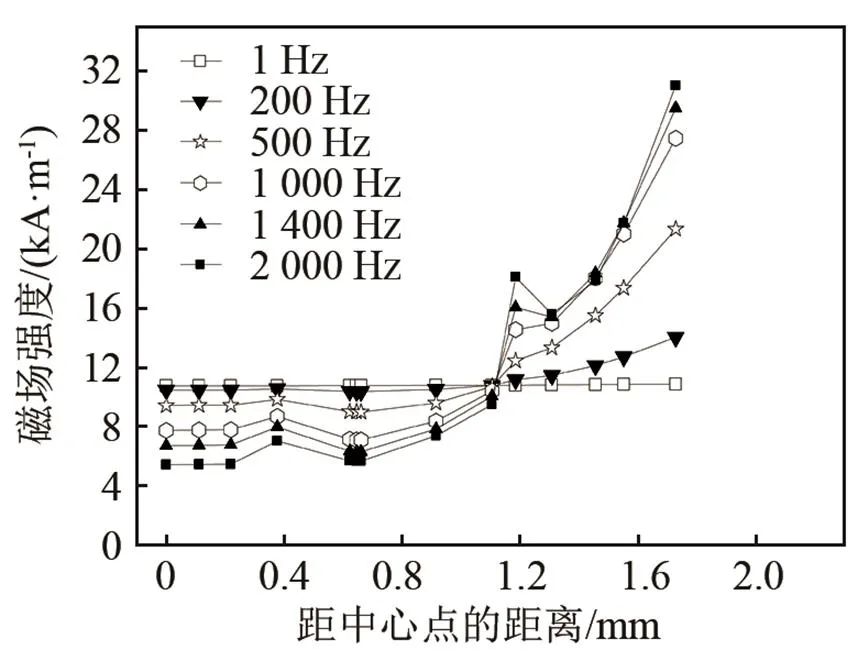
图6 换能器中磁致伸缩棒在不同频率下沿距中心点距离的磁场分布

采用公式计算和利用有限元方法计算得到的Fe-Ga合金应变值随频率变化的曲线如图7所示，横坐标为施加磁场的频率，纵坐标为换能器的应变值。随着施加磁场频率的增加，换能器的应变值会不断地减小，且减小的幅度不断降低。由图7可知，利用式(7)计算得到的曲线低于利用有限元方法计算得到的曲线，其原因在于公式计算的磁感应强度和磁场强度值来源于实验实测值，而实测值一般小于理论值，所以利用公式计算得到的曲线低于利用有限元方法计算的曲线。

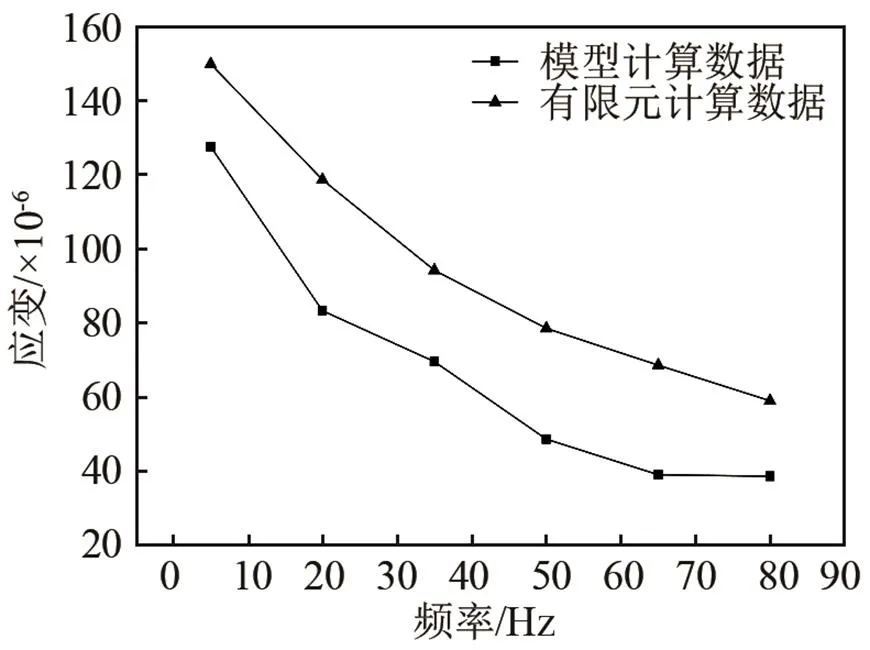
图7 换能器中磁致伸缩棒应变随频率变化的曲线

3.2 发音振子换能器的模态分析

Fe-Ga合金发音振子换能器在磁场频率为850～1 000 Hz频段内有振动峰，共振频率为984 Hz，如图8所示。

当对发音振子换能器施加的磁场频率达到984 Hz时，换能器的振型如图9所示。换能器的底端固定不动，Fe-Ga合金棒向上振动，从而带动弓张结构向外传递振动，，其中白色框架为振动前的结构模型，蓝色部分为振动后的结构模型，用来表现振动前后的变化。

图8 换能器的振幅随频率变化图

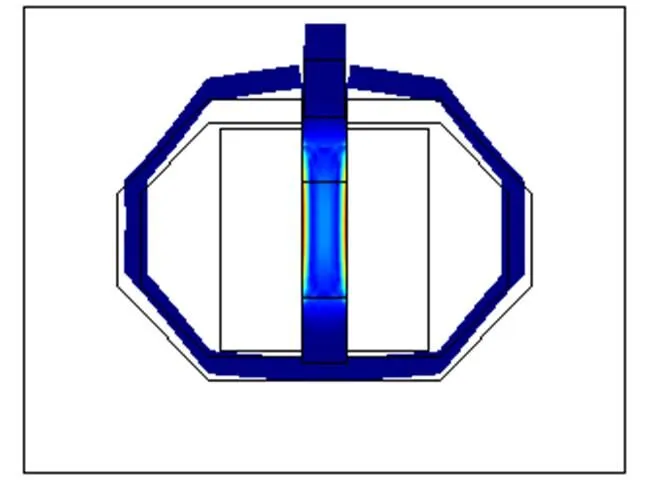
图9 换能器在984 Hz时的振型

4 实验验证

为了验证发音振子换能器的多场耦合模型的有效性，搭建了Fe-Ga合金棒磁致伸缩特性测试系统实验平台，如图10所示。

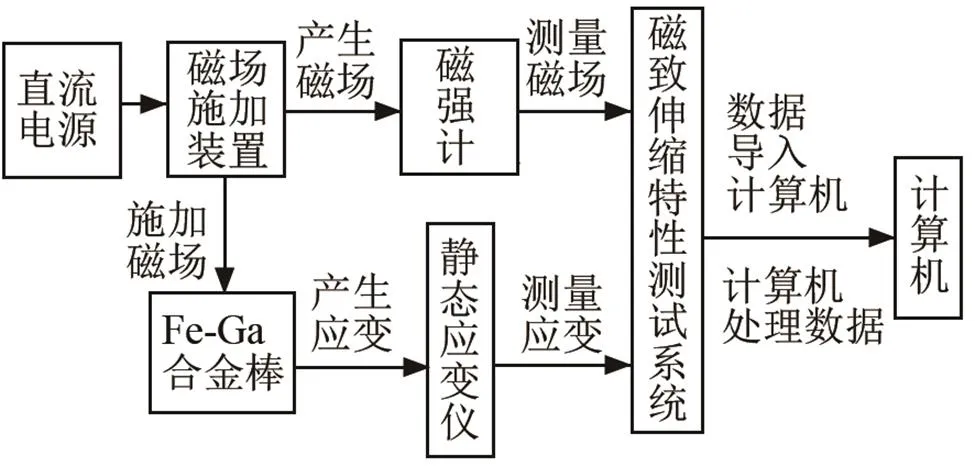
图10 Fe-Ga合金棒磁致伸缩特性测试系统

利用Fe-Ga合金棒磁致伸缩特性测试系统的直流电源和静态应变仪对Fe-Ga合金棒的静态应变曲线进行了测量。通过调节直流电源的电压来改变Fe-Ga棒上的磁场强度，从磁强计上读出对应的磁场强度数值，同时记录此时静态应变仪的读数，将磁场强度和应变值一一对应起来便绘制出Fe-Ga合金棒的静态应变曲线，如图11所示。对Fe-Ga合金棒进行了三次测试，三次的实验曲线基本重合，说明实验的可靠性高。随着磁场强度的增大，Fe-Ga棒的应变值也增大，当磁场强度达到40 kA·m-1时，应变值达到饱和，再增大磁场强度，应变基本不变。磁场强度为0～40 kA·m-1时，实验和模型计算结果吻合度较高；在40～120 kA·m-1时，实验结果略大于模型计算结果。磁场强度在40 kA·m-1时，实验测得饱和应变为70×10-6，模型计算的饱和应变为65×10-6。实验与模型计算结果基本一致，验证了多场耦合模型的有效性。

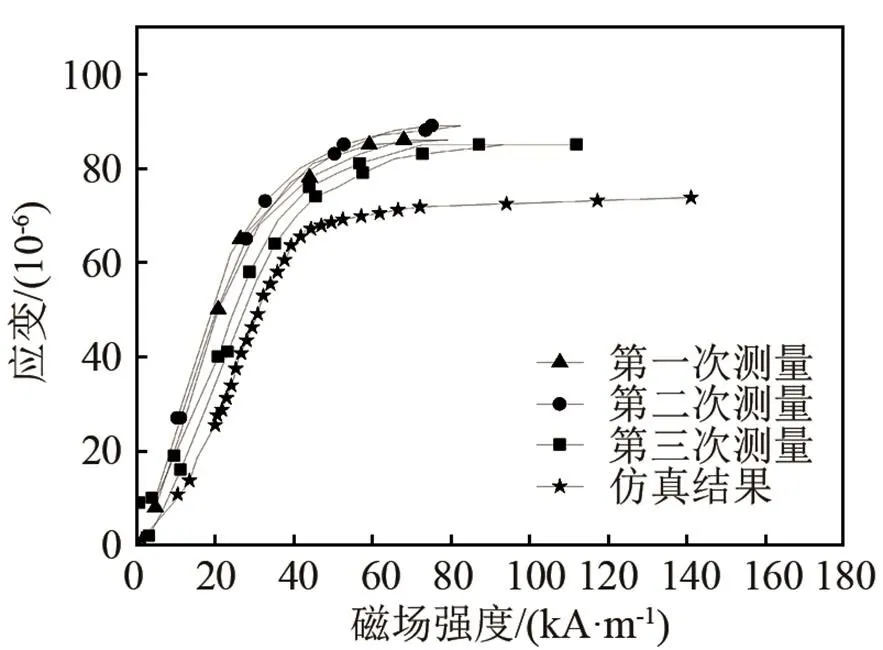
图11 Fe-Ga合金的磁场强度和应变的仿真及实验结果对比

磁致伸缩材料磁特性测试系统框图如图12所示。该系统由四个模块组成。施加磁场模块包括可变式直流稳压电源、函数信号发生器和功率放大器、励磁线圈等。信号测量模块包括轮式压力传感器、特斯拉计、霍尔传感器、磁通计、静态应变仪、动态应变仪。信号采集模块包括液晶显示模块、单片机控制模块、运算放大模块。数据处理模块包括计算机数据采集卡软件。

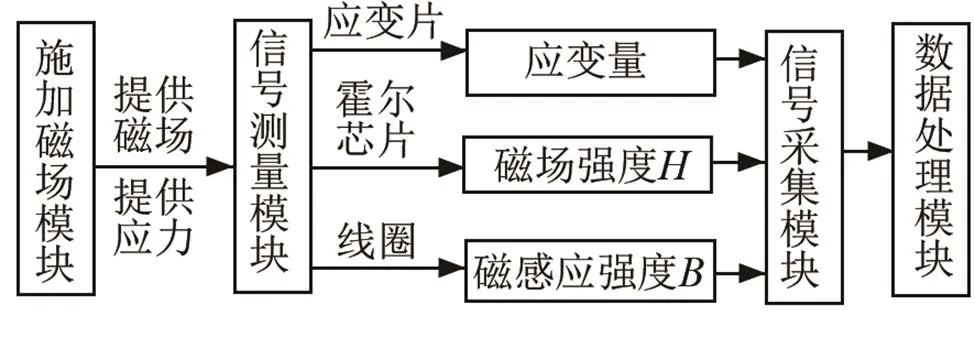
图12 磁致伸缩材料磁特性测试系统框图

利用磁致伸缩材料磁特性测试系统[15-16]，对弓张结构发音振子换能器Fe-Ga合金棒进行动态磁滞曲线测试，如图13所示。通过改变施加磁场模块中的励磁线圈电流的大小，控制磁场强度的最大值为0.6 kA·m-1，磁场的频率由5～50 Hz逐渐增大。在磁场强度大小不变的条件下，随着频率的增加，磁感应强度的最大值逐渐减小，其变化率逐渐减小，最后会趋于零。实验得到频率在50 Hz下Fe-Ga合金棒的最大磁感应强度为0.6 T，与图4模型得到的0.6 T对应，这表明模型计算结果与实验结果一致。

图13 不同频率下换能器中磁致伸缩棒的磁感应强度与磁场强度的动态曲线

利用磁致伸缩材料磁特性测试系统，测试了Fe-Ga合金棒的应变随磁场频率的变化关系，如图14所示。横坐标为施加磁场的频率，纵坐标为Fe-Ga合金棒的应变值。随着施加磁场频率的增加，Fe-Ga合金棒的应变值不断地减小，且减小的幅度不断降低。在50 Hz下实验得到的Fe-Ga合金棒外表面的应变值为77.42×10-6，与图7模型计算得到的78×10-6相对应，表明模型计算结果与实验结果一致。并且磁场频率在50～80 Hz之间时，模型计算结果

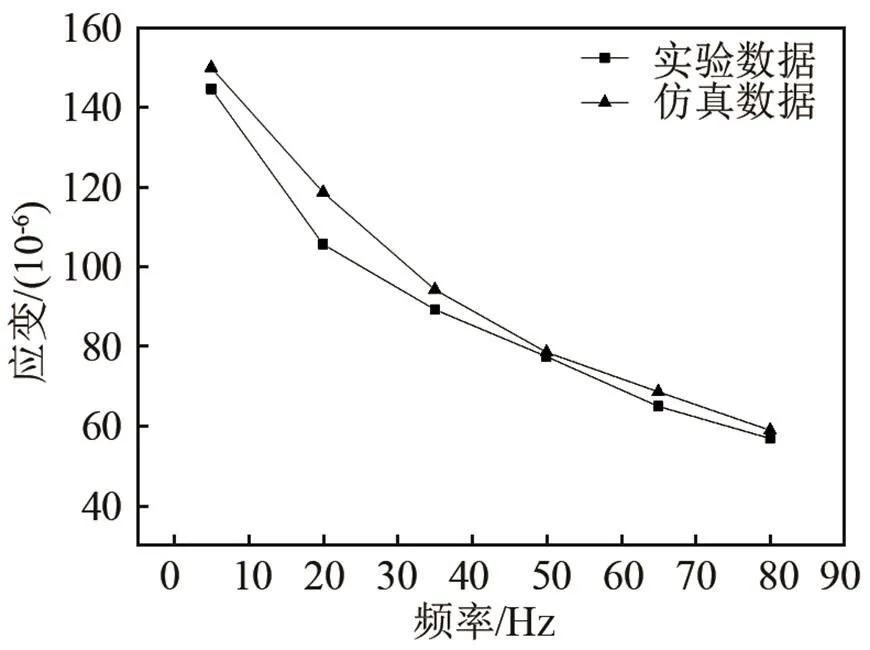
图14 换能器中Fe-Ga合金的应变随频率的变化曲线

与实验结果接近，验证了模型计算结果的正确性。由于Fe-Ga合金发音振子换能器制作加工的复杂性和条件的限制，短期内无法做出实物样机，后续将继续研究发音振子换能器的实际工作特性，并进行实验验证。

5 结论

利用COMSOL有限元仿真软件分析了发音振子换能器的磁场强度、磁感应强度、应变分布情况，并进行了换能器在不同频率下的磁场强度分析和模态分析。可得如下结论：

(1) 发音振子换能器的Fe-Ga合金棒轴线从底端向顶端2～8 mm处的磁场强度为7 kA·m-1，磁感应强度为0.6 T，棒中心点向外1 mm处的应变均匀为10×10-6。Terfenol-D棒的磁感应强度为0.25 T，棒的中心点向外1 mm处的应变为40×10-6，但棒的磁场分布不均匀。说明Fe-Ga合金材料更适合应用于发音振子换能器上。由模态分析可知，发音振子换能器的共振频率为984 Hz。

(2) 利用Fe-Ga合金棒磁致伸缩特性测试系统和磁致伸缩材料磁特性测试系统，分别测试了Fe-Ga合金静态应变曲线和动态磁滞曲线。当磁场强度的饱和值为40 kA·m-1时，应变为70×10-6，与模型计算的应变结果65×10-6一致。当磁场频率为50 Hz时，Fe-Ga合金棒最大磁感应强度为0.6 T，与模型计算的结果0.6 T一致。Fe-Ga合金棒外表面的应变值为77.42×10-6，与模型计算得到的78×10-6一致。

[1] 汪建新, 任翀, 高耀东. 一种磁致伸缩微位移器机械结构设计探讨[J]. 声学技术, 2007, 26(3): 528-533.

WANG Jianxin, REN Chong, GAO Yaodong. Design of mechanical structure of microdisplacement actuator using magnetostrictive materials[J]. Technical Acoustics, 2007, 26(3): 528-533.

[2] 杨兴旺, 陶伟明. 磁致伸缩材料Terfenol-D非线性耦合有限元分析[J]. 浙江大学学报(工学版), 2014, 48(11): 2094-2100.

YANG Xingwang, TAO Weiming. Finite element approach for nonlinear coupling analysis of magnetostrictive materials Terfenol-D[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(11): 2094-2100.

[3] 姜广军, 莫喜平. “音响虫”驱动薄板的振动特性有限元分析[J]. 声学技术, 2013,32(6): 486-489.

JIANG Guangjun, MO Xiping. Finite element analysis of the vibration characteristics of thin board actuated by a ‘soundbug’[J]. Technical Acoustics, 2013, 32 (6): 486-489.

[4] 王博文. 超磁致伸缩材料制备与器件设计[M]. 北京: 冶金工业出版社, 2003: 1-4.

WANG Bowen. Preparation and device design of giant magnetostrictive materials[M]. Beijing: Metallurgical Industry Press, 2003: 1-4.

[5] 翁玲, 吕稼先, 王跃虎, 等. 应力对Galfenol合金磁感应强度的影响[J]. 磁性材料及器件, 2016, 47(1): 1-4.

WENG Ling, LYU Jiaxian, WANG Yuehu, et al. Effect of stress on the magnetic induction of Galfenol alloy[J]. Journal of Magnetic Materials and Devices, 2016, 47(1): 1-4.

[6] JIA Z Y, LIU H F, WANG F J, et al. Research on a novel force sensor based on giant magnetostrictive material and its model[J]. Journal of Alloys & Compounds, 2011, 509(5): 1760-1767.

[7] 李全. 磁致伸缩振动发电机结构设计与实验研究[D]. 天津: 河北工业大学, 2015: 1-5.

LI Quan. Structural Design and Experimental Study of Magnetostrictive Vibration Generator[D]. Tianjin: Hebei University of Technology, 2015: 1-5.

[8] 朱晓峰. 骨导技术及在信息通信中的应用[J]. 电信技术, 2008(5): 18-20.

ZHU Xiaofeng. Bone conduction technology and its application in information communication[J]. Telecommunications Technology, 2008(5): 18-20.

[9] TRAN P, LETOWSKI T, MCBRIDE M. Bone conduction microphone: Head sensitivity mapping for speech intelligibility and sound quality[C]//International Conference on Audio, Language and Image Processing. IEEE, 2008, 7(8): 107-111.

[10] 曾平, 陈艳辉, 高莹莹, 等. 弹性支撑式压电骨传导听觉装置[J]. 光学精密工程, 2014, 22(10): 2765-2772.

ZENG Ping, CHEN Yanhui, GAO Yingying, et al. Piezoelectric bone-conduction hearing device with elastic support[J]. Optics and Precision Engineering, 2014, 22(10): 2765-2772.

[11] 曾平, 高莹莹, 董景石, 等. 三分频式压电骨传导助听装置的仿真与测试[J]. 光学精密工程, 2015, 23(4): 1011-1018.

ZENG Ping, GAO Yingying, DONG Jingshi, et al.Simulation and test of three-frequency piezoelectric bone conduction hearing device[J]. Optics and Precision Engineering, 2015, 23(4): 1011-1018.

[12] 曾平, 陈艳辉, 孙淑杰, 等. 矩形振子驱动式分频压电骨传导助听器[J]. 哈尔滨工程大学学报, 2015, 36(9): 1264-1268.

ZENG Ping, CHEN Yanhui, SUN Shujie, et al. Frequency division type piezoelectric bone-conduction hearing aid based on square and rectanglar vibrators[J]. Journal of Harbin Engineering University, 2015, 36(9): 1264-1268.

[13] 赵正龙, 何忠波, 李冬伟, 等. 弓张式GMM发音振子径向磁场仿真分析[J]. 压电与声光, 2015, 37(4): 672-675.

ZHAO Zhenglong, HE Zhongbo, LI Dongwei, et al. Simulation analysis of radial magnetic field distribution of GMM pronunciation vibrator with bow-type structure[J]. Piezoelectrics & Acoustooptics, 2015, 37(4): 672-675.

[14] 曹淑瑛, 王博文, 闫荣格, 等. 超磁致伸缩致动器的磁滞非线性动态模型[J]. 中国电机工程学报, 2003, 23(11): 145-149.

CAO Shuying, WANG Bowen, YAN Rongge, et al. Dynamic model with hysteretic nonlinearity for a giant magnetostrictive actuator[J]. Proceedings of the CSEE, 2003, 23(11): 145-149.

[15] 翁玲, 赵青, 孙英, 等. 考虑附加涡流损失的Galfenol合金动态滞后建模与实验[J]. 农业机械学报, 2016, 47(4): 399-405.

WENG Ling, ZHAO Qing, SUN Ying, et al. Dynamic hysteresis model and experiment of galfenol alloy considering excess eddy current losses[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(4): 399-405.

[16] 翁玲, 胡秀玉, 赵青, 等. Fe-Ga合金换能器动态输出特性分析[J]. 传感技术学报, 2017, 30(6): 836-840.

WENG Ling, HU Xiuyu, ZHAO Qing, et al. Analysis of dynamic output characteristics of Fe-Ga transducer[J]. Chinese Journal of Sensors and Actuators, 2017, 30(6): 836-840.

Multi-field coupling model of vocal vibrator transducer of Fe-Ga alloy

WENG Ling, LI Wei-na, LIANG Shu-zhi, XU Hang

(The State Key Laboratory of Reliability and Intelligence of Electrical EquipmentHebei University of Technology, Tianjin 300130, China)

In this paper, the multi-field coupling model of electric field, magnetic field and solid mechanic field for the bow-shaped vocal vibrator transducer of Fe-Ga alloy is established. The distributions of magnetic field intensity, magnetic induction intensity and strain of the transducer are studied, and the magnetic field intensities at different frequencies and the modal characteristics of the vocal vibrator transducer are analyzed. It is found that the magnetic field intensity of the bow-shaped vocal vibrator transducer of Fe-Ga alloy is reduced with the increase of frequency, and the resonant frequency of the transducer is calculated to be 984 Hz. The relationship between the magnetic field strength and the strain of the core component Fe-Ga alloy in the transducer is tested. When the saturation value of the magnetic field is 40 kA/m, the strain is 70 × 10-6. The hysteresis curves of Fe-Ga alloy at the magnetic field frequencies of 5 Hz, 20 Hz and 50 Hz are measured by the magnetic property testing system for magnetostrictive material. And the frequency response curve of Fe-Ga alloy rod is tested, the experimental result is consistent with the strain simulation result of Fe-Ga alloy in the transducer.

Fe-Ga alloy; modal characteristics; multi-field coupling model; vocal vibrator

TN64

A

1000-3630(2018)-06-0612-06

10.16300/j.cnki.1000-3630.2018.06.018

2017-11-20;

2017-12-21

国家自然科学基金资助项目(51201055，51777053)；河北省引进留学人员资助项目(CG2013003001)；河北省高等学校科学技术研究重点项目(ZD2015085)

翁玲(1978－), 女, 河南信阳人, 博士, 副教授, 硕士生导师,研究方向为磁性材料与器件。

翁玲, E-mail: llweng@hebut.edu.cn