正组合曲率带边有限图的分类

苏延辉

(福州大学数学与计算机科学学院， 福建 福州 350116)

0 引言

组合曲率是由文献[1-3]引入的， 其基本想法是将图嵌入到分片平坦的曲面并利用广义高斯曲率来定义. 设(V,E)为局部有限的无向简单图， 若其拓扑嵌入到曲面S内则称其为半平面图； 若S同胚于2或单位球面， 则称其为平面图. 记G=(V,E,F)， 这里F为面的集合, 不失一般性， 做如下细分假定：

1) 每个面均同胚于一个圆盘， 其边界由图上的有限个边组成；

2) 每个边恰包含于两个不同的面；

3) 任意两个面， 如果其闭包具有非空的交集， 则交集或者为一个顶点或者为一条边.

在上述定义下， 图的组合曲率定义为：

(1)

为了进一步理解其几何意义， 将图G的每条边取为单位长度， 每个面用同样边数正多边形替代(由此得到的曲面称为正多边形曲面, 记为S(G))则组合曲率乘以2π即为该点处的广义高斯曲率.

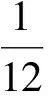
本研究将分析具有正曲率带边有限图的分类问题. 称G=(V,E,F)为带边有限图， 如果其嵌入曲面为带边曲面. 不失一般性， 设图G满足上述细分假定的1)和3)， 并将2)替换为2′): 曲面S的边界∂S由图的边组成， 图的每条边(除去端点外)或者位于∂S， 或者位于S的内部. 在前一情形该边邻接一个面， 而后一情形该边邻接两个面. 更进一步， 假定边界顶点的度2≤deg(x)<∞， 而内部顶点的度3≤deg(x)<∞. 边界点的组合曲率仍按(1)式给出.

1 基本事实

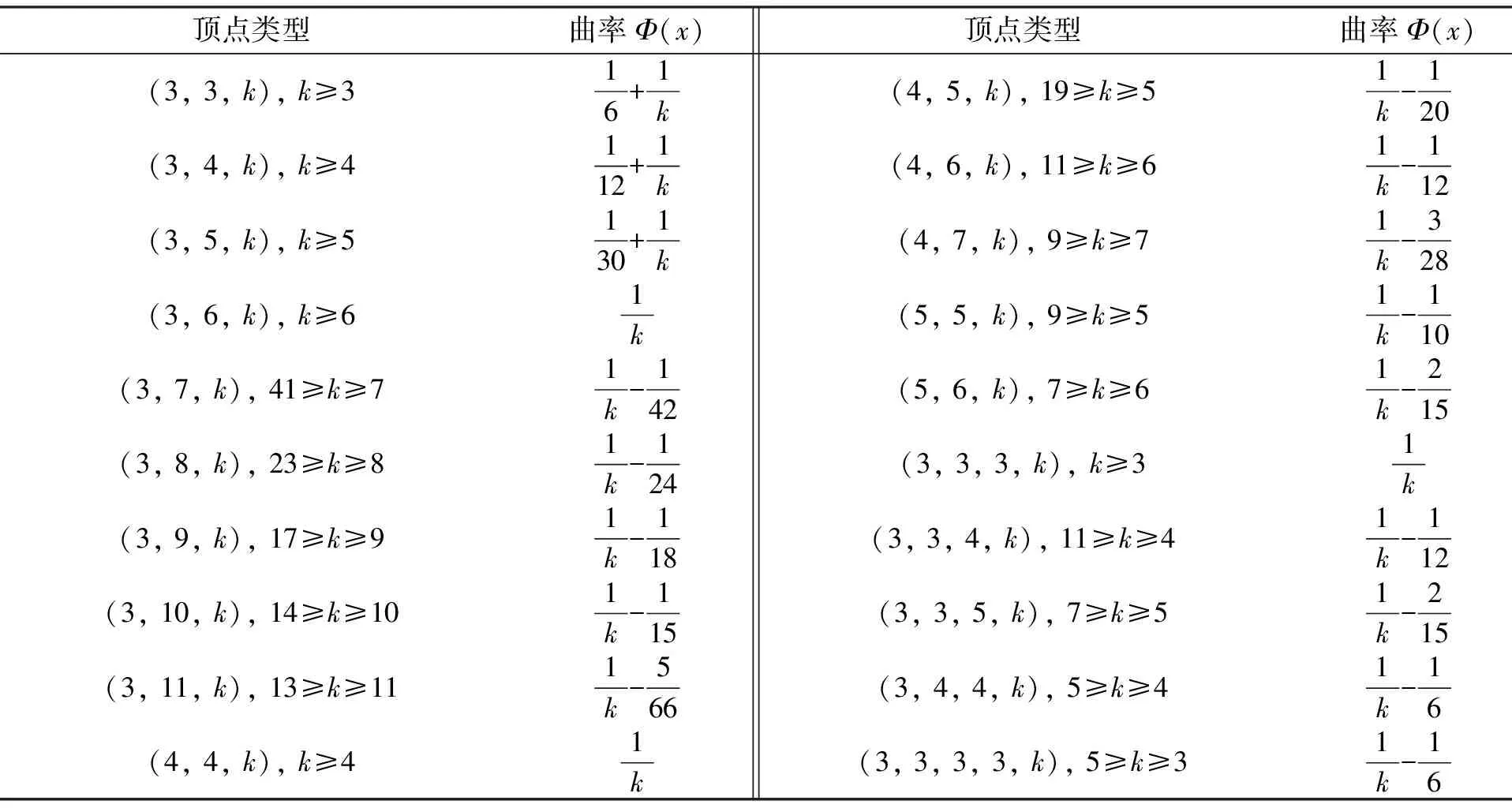
表1 正曲率内部顶点类型及相应曲率值

2 正组合曲率带边有限图的分类定理的证明

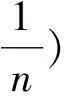
定理1除去正n边形这一平凡情形外， 带边正曲率有限图共有71种互不同构的类型.

证明 本证明其实就是构造全部互不同构的有限图的过程. 首先注意到一个很简单的事实—图的多边形曲面的边界上至少含有三角形的边, 下面分两类图形讨论.

图1： 若某三角形有两条边在边界上.

该情形下， 三角形的余下一条边可以邻接其他多边形， 在曲率为正的假设下， 只能邻接3边形、 4边形和5边形. 再进一步在正组合曲率的假设下考虑这些多边形是否可能继续邻接多边形(需要注意的是要满足细分假设以及正组合曲率条件)， 最终得到以下11种互不同构的有限图.

图1 若某三角形有两条边在边界上Fig.1 There is a triangle with two edges on the boundary

图2： 所有三角形均至多有一条边在边界上.

取定一个某条边位于边界的三角形， 考虑其邻近多边形的情况. 由细分假设， 两条位于内部的边界必邻接不同的多边形， 按照可能的粘合情况， 共有如下12种情形.

图2 所有三角形均至多有一条边在边界上Fig.2 All triangles with one edge on the boundary

这里a,b,c表示位于边界上的边， 而其他边可能是正多边形曲面的边界， 也可能不是正多边形曲面的边界. 首先注意到的一个简单的事实是： 情形(2)、 情形(4)和情形(6)已构成正曲率有限图， 且它们是仅有的(与图1不同构的)可能. 下面考虑其他九种情形.

情形(1)： 考虑除a,b,c外的其他边邻接多边形的可能(同样需要注意满足细分假设以及正组合曲率条件)， 情形(1)会产生如下6种互不同构(且与前述情形也互不同构)的正曲率有限图, 详见图3.

图3 情形(1)的6种可能Fig.3 There are six possibilities in case (1)

情形(3)： 用相同的办法， 可以得到该情形下会产生如下6种互不同构(且与前述情形也互不同构)的正曲率有限图, 详见图4.

图4 情形(3)的6种可能Fig.4 There are six possibilities in case (3)

情形(5)： 做法与前述情形相同， 但由于五边形每个顶点具有较小的曲率， 因此可能的情形较多， 可以得到该情形下会产生如下11种互不同构(且与前述情形也互不同构)的正曲率有限图, 详见图5.

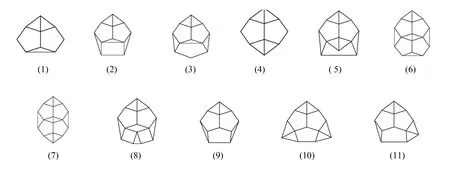
图5 情形(5)的11种可能Fig.5 There are eleven possibilities in case (5)

情形(7)： 可以得到该情形下会产生如下8种互不同构(且与前述情形也互不同构)的正曲率有限图,详见图6.

图6 情形(7)的8种可能Fig.6 There are eight possibilities in case (7)

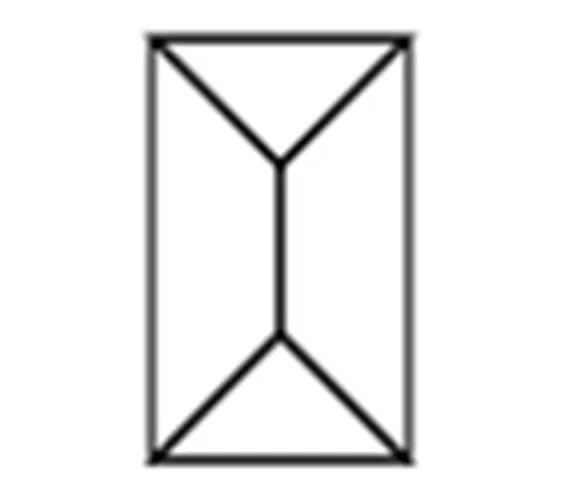
图7 情形(8)的1种可能Fig.7 There are is only one possibility in case (8)

情形(8)： 该情形由于两个四边形共一条边， 导致从属于三角形和两个四边形的那一顶点具有较大的曲率， 该情形下只产生1种(与前述情形也互不同构)的正曲率有限图， 见图7.

情形(9)： 可以得到该情形下会产生如下13种互不同构(且与前述情形也互不同构)的正曲率有限图, 详见图8.

图8 情形(9)的13种可能Fig.8 There are thirteen possibilities in case (9)

图9 情形(10)的1种可能 Fig.9 There is only one possibility in case (10)

情形(10)： 同情形(8)一样， 该情形只得到1种互不同构(且与前述情形也互不同构)的正曲率有限图, 见图9.

情形(11)： 该情形与情形(5)相似， 由于五边形具有较小的曲率， 因此可能出现的图形较为复杂， 该情形下可以产生如下9种互不同构(且与前述情形也互不同构)的正曲率有限图. 更为有趣的是该情形下的第六个图和第七个图中间的多边形边数分别为6和7， 而且这两个图具有很好的对称性, 具体见图10.

图10 情形(11)的9种可能Fig.10 There are nine possibilities in case (11)

图11 情形(12)的2种可能 Fig.11 There are two possibilities in case (12)

情形(12)： 该情形只得到2种互不同构(且与前述情形也互不同构)的正曲率有限图, 见图11.

以上即为全部互不同构的类型. 证毕！

上述定理完成了正组合曲率带边有限图的完全分类， 这些图中有许多对称性很高的图. 值得注意的是情形(11)中的第七个图顶点数为28， 它是所有图中顶点数最大的. 于是本研究有如下推论：

推论1除去正n边形这一平凡情形外， 带边正曲率有限图最大顶点数为28.