基于VAR模型的货币政策有效性研究
2019-01-10黄志刚林朝颖
黄 乐, 黄志刚, 林朝颖
(1. 福州大学经济与管理学院, 福建 福州 350116; 2. 福建省金融科技创新重点实验室, 福建 福州 350116; 3. 福建农林大学管理学院, 福建 福州 350002)
0 引言
2009年11月3日, 前国务院总理温家宝在《让科技引领中国可持续发展》的重要讲话中首次提出了战略性新兴产业(strategic emerging industries, SEI)的概念. 2010年10月, 文献[2]第一次明确提出了我国发展战略性新兴产业的目标. 2016年12月19日, 经李克强总理签批, 国务院印发《“十三五”国家战略性新兴产业发展规划》[3], 其中更是对“十三五”期间我国战略性新兴产业发展目标、 重点任务、 政策措施等做出了全面的部署和安排. 对于战略新兴产业的划分, 周晶等[4]从统计学的角度, 对战略新兴产业进行统计分类. 国内更多的学者是从财政政策的角度对战略新兴产业开展研究, 李苗苗等[5]从财政政策、 企业R&D经费和技术创新能力三个方面对战略新兴产业进行实证分析, 提出政府应设定适当财政政策门槛, 才能使其产生积极作用. 文献[6-7]分别从甘肃、 内蒙古的区域财政政策对战略新兴产业的影响来验证其重要性及作用.
纵观历史, 发达国家历经200多年的工业现代化道路是以牺牲资源和环境作为代价的. 如今包括中国在内的发展中国家为了实现现代化, 不能再走发达国家所走的老路, 必须依靠科学技术形成投入少、 产出多、 少排放、 多利用的新型生产消费模式, 真正实现可持续发展. 进入21世纪以来, 一些重要科技领域取得了革命性的突破, 一场由知识和技术体系创新所驱动的科技革命即将发生, 这必将为人类世界现代化进程提供强大的动力. 中国必须抓住这次发展契机, 缩小与世界先进科技水平的差距, 顺应世界经济科技发展的大趋势, 从中赢得主动、 有所作为. 如何能更好地扶持发展战略新兴产业, 使其逐步成为我国经济社会发展的主导力量, 是当下所要解决的重点问题.
货币政策有效性是研究经济学的一个重要内容, 也是宏观经济预测和货币政策制定的理论基础. 诸多学者对其都有深入的研究, Friedman等[8]最早运用时间序列计量方法来考察货币政策和财政政策对名义产出影响的显著程度. Sims[9]则从产出维度研究货币政策变量的作用效果. 国内的学者也对货币政策有效性有深入的研究, 文献[10]揭示我国货币政策冲击在不同的时间维度对实体经济的影响也不同. 文献[11]通过实证证明货币供应量作为我国货币政策研究的中介目标仍然有效. 闫力等[12]运用VAR模型对我国货币政策有效性进行分析, 实证表明货币供应量M1价格效应比产出效应明显. 文献[13]利用中国30个工业两位数行业数据建立SVAR模型分析货币政策的微观传导机制.
除此之外, 国内还有很多学者研究货币政策在不同行业中的有效性, 其中研究最多的就是房地产行业. 文献[14]通过建立VAR模型, 运用脉冲响应函数与方差分解方法研究货币供应量与利率冲击对房地产价格的动态影响, 发现货币供应量对房价有正向影响, 利率的变化则会使房地产价格下降. 高波等[15]的研究表明, 货币供给量的增加会刺激房地产投资和商品房销售额的增长, 提高利率则对贷款供给是有效的.
自2008年金融危机以来, 我国广义货币供应量M2大幅增加, 截至2017年8月末, 达到164.5万亿元, 平均同比增长15.51%; 同时, 公共财政支出也从2008年的6万亿, 增加到2016年的18.8万亿, 平均同比增长16.07%. 越来越多的学者关注到财政政策对战略新兴产业的影响, 却忽略了货币政策对战略新兴产业的作用. 本研究希望通过构建VAR模型, 研究货币政策在战略新兴产业的有效性, 从而为制定有效的战略新兴产业货币政策提供理论依据. 目前还没有专家学者运用VAR模型对货币政策在战略新兴产业中的有效性进行过验证, 本研究很好地弥补了这一空缺, 可以为战略新兴产业货币政策的有效性提供有力的理论支持.
1 变量选择和数据说明
1) 变量选择. 在文献[16]研究的基础上, 考虑到我国利率尚未完全自由化, 利率并不能完全反映货币市场的供求状况, 故选取货币供应量M2代表货币政策. 对于战略新兴产业的研究, 国内的学者更多探讨财政政策对其的影响, 为了使模型更全面地反映问题, 选择公共财政支出作为财政政策的代表, 研究其对战略新兴产业的影响. 同时, 分别采用我国工业生产总值和战略新兴产业的主营业务收入作为衡量货币政策以及财政政策对该行业的影响. 最后, 为了熨平数据的长期趋势, 本研究对所有数据取其自然对数, 分别记为M2, FP, GDPi, SEI.
2) 数据来源. 所选的样本区间为2004年1月到2015年9月的季度数据. 所有原始数据均来自《中国统计》《中国高科技产业统计年鉴》和Wind数据库. 战略新兴产业的数据是根据文献以及国家发改委《战略新兴产业重点产品和服务指导目录》(2016)中对战略新兴产业各行业的划分, 通过整理并对原始数据以X-11方法进行季节调整处理得出. 本研究所有计量分析工作都使用Eviews 8.0软件完成.
2 计量模型及分析
根据上文所选变量及数据, 建立如下向量自回归(VAR)模型:
(1)
其中:Yi, t=(GDPi,M2, FP, SEI),M2为货币政策中介目标的货币供应量;Ai为系数向量;k为模型的滞后阶数;εi, t为白噪声误差项;di是常数项. 展开式为:
自回归模型采用的是多方程联立的形式, 它并不以经济理论为基础, 在模型的每一个方程中, 内生变量对模型的全部内生变量的滞后项进行回归, 从而估计全部内生变量的动态关系.
在对VAR模型进行估计之前, 必须对时间序列的平稳性进行检验, 以防止缪误回归的发生. 常见的方法有Dickey-Fuller检验(DF检验)、 扩展的Dickey-Fuller检验(ADF检验)和Phillips-Perron检验(PP检验). DF检验适用于一阶自回归且无时间趋势的时间序列检验, ADF检验适用于高阶回归时间序列的检验, PP检验则是在检验模型中不引入滞后项. 本研究采用ADF检验方法对各时间序列变量的平稳性特征进行检验, 并对非平稳序列进行修正, 使一阶差分后的非平稳序列成为平稳序列, 检验结果如表1.

表1 单位根检验结果
注: ① D为时间序列的一阶差分形式; ② 检验形式(C、T、L)中的C表示ADF检验时有常数项,T表示含有时间趋势项(T为0时, 表示不含有时间趋势项),L表示滞后阶数, 选取规则遵循模型中随机误差项不存在序列相关关系; ③*、**、***分别代表时间序列在10%、 5%、 1%的显著水平下是平稳的
如表1所示, 所有原时间序列都是不平稳的, 经过一阶差分之后在1%的显著性水平上都是平稳的, 所以GDPi、M2、 FP、 SEI都是一阶单整时间序列. 为了检验这些变量之间有没有存在长期稳定的均衡关系, 本研究采用Johansen协整检验的方法, 根据最优滞后阶数选择的原则, 将VAR模型的最优滞后阶数设定为1, 检验结果如表2所示.
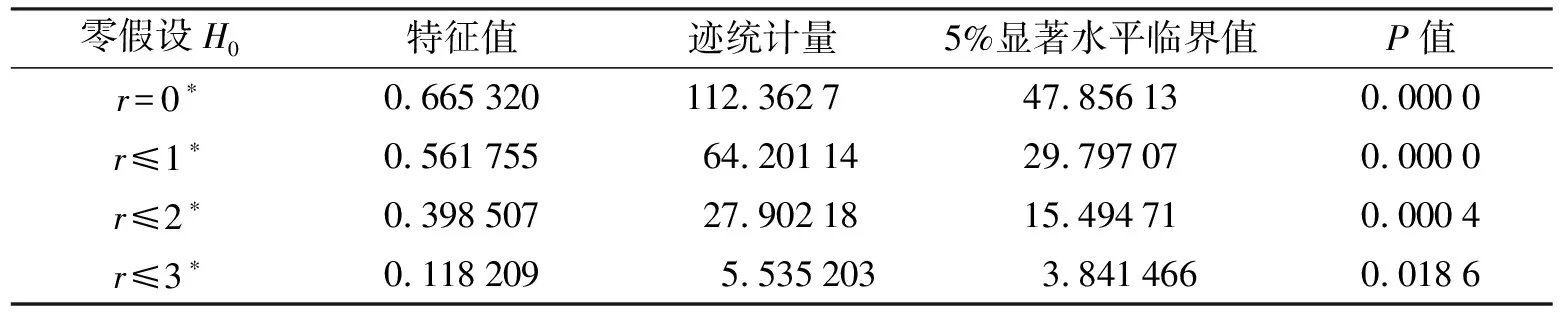
表2 Johansen协整检验结果
注:r表示协整关系的个数

表3 格兰杰因果关系检验结果
由检验结果可见, GDPi、M2、 FP、 SEI之间存在4个协整关系, 这就意味着这些非平稳时间序列之间有长期均衡的关系. 为了进一步证实货币供应量、 公共财政支出和工业生产总值是否会对战略新兴产业的产出带来影响, 本研究进行格兰杰因果关系检验, 结果见表3. 从上述检验中发现, 在90%的置信水平上, 货币供应量M2、 工业生产总值和公共财政支出都是战略新兴产业产出波动的主要原因. 也就是说货币供应量、 工业生产总值和公共财政支出的变动都对战略新兴产业的产出有显著的影响.
为了具体分析货币政策和财政政策如何影响战略新兴产业的产出, 特别是在其他因素保持不变的前提下, 分析货币供应量M2、 工业生产总值和公共财政支出的冲击对战略新兴产业产出的动态影响, 脉冲响应函数提供了很好的解释. 如图1所示, 在当期分别给货币供应量M2、 工业生产总值和公共财政支出一个Cholesky标准差的正向冲击, 来观察战略新兴产业的产出分别对它们有什么反应.

图1 脉冲响应Fig.1 Impulse response
1) 财政政策. 公共财政支出的增加会刺激战略性新兴产业产出的上涨. 在给当期公共财政支出一个单位的正向冲击之后, 战略新兴产业的产出马上就有一个小幅的增长. 因为财政政策一开始没有明确的目标性, 所以对于整个行业的扶持会给总产值带来短时间的增加; 随之而来的是一个大幅的降低, 通过市场的筛选, 一些能耗过高或是没有太大市场竞争力的产品会被市场规律所淘汰, 所以导致产出的降低. 进入下一时期后, 由于市场筛选留下的企业具有更强的竞争力, 所以这时的财政政策就具有较为明确的目标性, 会使产出继续增长. 之后会重复这一筛选过程, 直至整个市场趋于稳定, 整个战略新兴产业产出对财政政策单位冲击的累积响应约为1.4%.
2) 货币政策. 货币供应量的增加短期内抑制战略新兴产业产出的增长. 在给当期货币供应量一个正向的冲击之后, 战略新兴产业的产出会出现一个明显的负增长, 直到第2期才出现增长的趋势, 之后一直保持增长趋势. 因为当货币供应量增加的时候, 对传统产业来说, 获取资金更加容易, 会刺激对传统产业的投入及其产量的增加, 相对而言战略新兴产业获得的投资较少, 在短期内会对战略新兴产业的产出产生“挤兑效应”. 之后由于产量的提升, 假定需求不变, 市场将出现供大于求现象, 导致通货膨胀, 但是战略新兴产业多为高科技产品, 有财政政策的补贴, 价格相对稳定, 所以会导致战略新兴产业产出相对与传统产业有较大提升. 整个战略新兴产业产出对货币政策单位冲击的累积响应约为3.5%, 可以看出效果非常显著.
3) 工业生产总值. 工业生产总值的增加会使战略性新兴产业产出同时增加. 在给当期工业生产总值一个单位的正向冲击之后, 并不会立刻对战略新兴产业的产出有影响, 但在第2期会有正面影响且波峰达到为3.2%, 之后慢慢达到新的平衡, 整个战略新兴产业产出对工业生产总值单位冲击的累积响应约为3.2%.
3 结语
本研究创新性地运用VAR模型对货币政策在战略新兴产业中的有效性进行分析, 对2004年1月到2015年9月的经济金融季度数据进行收集. 通过单位根检验、 协整检验和格兰杰因果检验来确定模型的稳定性, 再利用脉冲响应函数来观察战略性新兴产业产出对货币政策和财政政策冲击的反应. 根据理论分析和实证检验, 本研究发现货币政策在战略新兴产业方面是有效的, 且货币政策累积响应约为3.5%, 财政政策的累积响应约为1.4%, 工业生产总值的累积响应约为3.2%.
工业生产总值、 货币供应量以及公共财政支出互为因果关系, 所以工业生产总值的增加也会通过货币供应量和公共财政支出这两个渠道间接地影响战略新兴产业的产出, 至于如何传导与影响可待后续研究. 货币供应量的增加, 在短期内会对战略新兴产业的产出产生“挤兑效应”, 但从长期来看肯定对繁荣战略新兴产业是有利的. 对于财政政策, 正如很多学者研究的, 对战略新兴产业具有很强的正相关性, 通过专项财政支出和税收补贴等方式, 财政政策可以有效地刺激战略新兴产业产出的增长, 配合市场的筛选过程, 能够更好地选出真正具有市场竞争力的产品, 这也是战略新兴产业在宏观经济疲软时期仍能保持快速增长的重要保障. 因此, 在财政政策的扶持下, 还应注意货币政策的调控, 才能更好更快地促进我国战略新兴产业的发展.
向量自回归模型可以很好地反映内生变量之间的动态关系. 同时, VAR模型允许变量的值取决于其自身的滞后项和其他变量的滞后项. 而且该模型提供了丰富的结构信息, 能够捕获更多的数据特征. 因此, 由VAR产生的预测通常比传统的结构模型来的更好. 在实际应用中, 如果滞后阶数足够大, 模型可以完全反映所有的动态关系信息. 但是它有一个严重的缺点, 如果滞后阶数越大, 待估计的参数就会越多, 然后自由度就会下降. 所以, 找到自由度与滞后阶数之间的平衡点至关重要.
