AANA阵列的完全收敛性
2019-01-10王宽程杨英钟高小明
王宽程, 杨英钟, 高小明
(闽南理工学院信息管理学院, 福建 泉州 362700)
0 引言
称随机变量是X1,X2, …,Xn,n≥2是负相关(negatively associated, NA)的, 如果对于1, 2, …,n的任何两个不交的非空子集T1和T2都有
Cov(f(Xi,i∈T1),g(Xj,j∈T2))≤0
其中:f和g是任何两个使上述协方差存在且对每个变元均非降(或均非升)的函数.
称随机变量列{Xn,n∈N}是NA的, 如果对任何自然数n≥2,X1,X2, …,Xn都是NA的; NA序列由文献提出, 有关NA序列的研究可以参考文献[2-4].
称{Xn;n∈N}为渐近几乎负相关(asymptotically almost negatively associated, AANA)随机变量序列, 如果存在非负序列q(n)→0(n→∞), 对任意的n,k≥1都有
Cov(f(Xn),g(Xn+1, …,Xn+k))≤q(n)(Var(f(Xn))Var(g(Xn+1, …,Xn+k)))1/2
其中:f和g是任何两个使上述方差存在且对每个变元均为非降的连续函数; {q(n);n∈N}为该序列的混合系数.
称随机阵列{Xnk; 1≤k≤n,n∈N}是行为AANA阵列, 固定n, 假设每一行内的随机变量列{Xnk}是AANA的.
AANA序列是包含独立列和NA列(令q(n)=0,n≥1)的更为广泛的随机变量序列. 显然, 如果随机变量序列是NA列, 则它们一定是AANA列, 反之不真. 此外, AANA序列也不同于渐近负相关(asymptotically negatively associated, ANA)列. 近年来有关AANA序列的研究, 已取得不少的成果. 如文献研究了AANA重对数定律和强大数定律; 文献[8-9]分别得到了AANA的Hajek-Renyi不等式和Rosenthal型不等式; 文献[10]讨论了AANA部分和的极限; 文献[11]研究了AANA的极大不等式和强大数定律; 文献[12]研究了AANA加权和的强大数定律. 本研究分析AANA阵列在h-可积下的完全收敛性以及AANA阵列在p阶Cesaro一致可积条件下的完全收敛性, 得到并推广NA序列的相应结果.
1 预备知识
定义1[13]k≤n,n∈N}是p阶cesaro一致可积的, 若
定义2[14]称阵列{Xnk; 1≤k≤n,n∈N}关于常数阵列{ank; 1≤k≤n,n∈N}是h-可积的, 若满足下列条件:

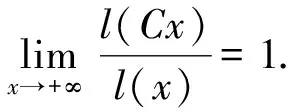
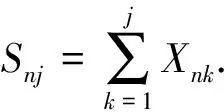
2 结论
引理1设{Xn;n∈N}为AANA序列, 并且混合系数是{q(n);n∈N}, 若{fn;n∈N}皆是单调非降(或者单调非增)连续函数, 那么{fn(xn);n∈N}仍然是AANA序列, 其混合系数仍然是{q(n);n∈N}.

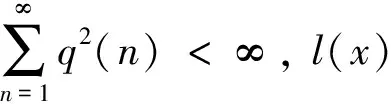
则对αp≥1有
(∀ε>0)(1)
证明 取x=nα(2-p)/4, 当n→∞时,x→∞, 对Xnk截尾, 记
故为证(1), 只需证I1<∞,I2<∞.
由Morkov不等式, 及引理2有

又因为x=nα(2-p)/4, 所以∃N>0, 使得当n≥N时, 有x>M故
定理证毕.
特别令q(n)=0(n≥1)则可得下列推论.
推论1设{Xn;n≥1}是NA列,l(x)为缓变函数, 且对1
则对αp≥1, 有
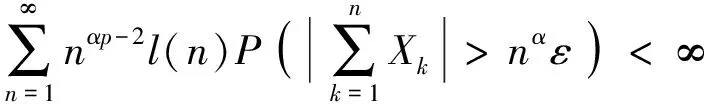
定理2设{Xnk; 1≤k≤n,n≥1}为零均值且EXnk<∞的行为AANA阵列,l(x)为缓变函数, {ank}是常数阵列, {h(n)}是单调不减序列且h(n)→∞(n→∞). 设α>0,αp>1, 0<δ<1,q>0,t>0为实数, 满足:αp-α-q<0,αp-t+1<0及α-q+1<0. 如果下面3个条件成立:
i) {Xnk}是关于常数阵列{ank}的h-可积, 且maxank=O(n-ql-1(2k));
则有
(∀ε>0)(2)
证明 对每个1≤k≤n(n≥1), 令
Ynk=XnkI(Xnk≤h(n))-h(n)I(Xnk<-h(n))+h(n)I(Xnk>h(n))
由引理1可知{Ynk; 1≤k≤n,n≥1}仍为AANA阵列.
先证
因为∀ω∈Dn, 有
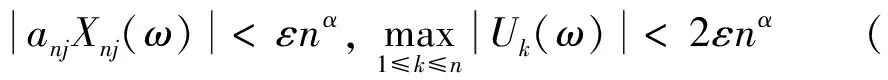
且∀1≤i Xni(ω)≤h(n)或Xnj(ω)≤h(n),Xni(ω)>=-h(n)或Xnj(ω)>=-h(n) 若记a=#{i:1≤i≤n,Xni(ω)>h(n)},b=#{i:1≤i≤n,Xni(ω)<-h(n)}. 则易知a≤1,b≤1. 当a=0,b=0时, 有∀j(1≤j≤n),anjXnj(ω)≤anjh(n), 所以anjXnj(ω)=anjYnj(ω), 从而 当a=1,b=0时, 仅有某个i0, 使得Xni0(ω)>h(n), 但仍有ani0Xni0(ω)<εnα, 而其余的i, 都有aniXni(ω)=aniYni(ω).若1≤k≤i0-1, 则Sk(ω)=Uk(ω); 若i0≤k≤n, 则 Yi0(ω)=h(n) 从而 同理可证当a=0,b=1时及当a=1,b=1时的情况, 故式(3)成立.因此, 有 所以要证式(2), 只需证明: 先证式(4) 再证式(5) 要证式(6)成立, 只需证 由引理2及条件ii)可得 定理2证毕.
