从欧几里得《几何原本》谈公理化思想
2019-01-10何红英
何红英
(西安市职工大学 基础部,西安 710068 )
最早的几何学兴起于公元前7世纪的古埃及,后经古希腊人传到了希腊的都城——雅典.那时人们已经积累了许多几何学的知识.这些知识很多都是零星的、碎片式的,缺少彼此之间的联系和系统性.
古希腊哲学家、思想家柏拉图(前427—前347)在经历了十二年避风式的周游后回到雅典,于圣城阿卡德谟创立了他个人讲学的园地——阿卡德谟创学园[1].柏拉图在这里开始教演讲术,著书立说.柏拉图提倡孩子们首先要接受完备的体育训练,但是音乐、数学以及其他学科也要重视.学习几何被认为是寻求真理的最有效的途径.柏拉图甚至声称:“上帝就是几何学家”.越来越多的希腊市民向往进入学园学习,也就越来越喜欢几何.在学园里,师生之间的教学活动完全通过对话形式进行.这种问答、质疑、讨论的对话互动过程,最能激发人们的想象,培养抽象思维、逻辑思维的能力.对话过程中的思维是最活跃的,而思维是智力的核心.因此学园培养的学生都具有超强的抽象思维能力.
欧几里得(前330—前275)就是在这个时期出生于雅典,古希腊文明中心浓郁的数学文化气氛深深地感染了他,在他十几岁时,就迫不及待地进入了“柏拉图学园”.在这里,欧几里得翻阅了柏拉图的所有著作和手稿,研究柏拉图的学术思想和数学理论.欧几里得认为进行“智慧训练”就应该从以图形为主要研究对象的几何学开始,因此,他给自己确定的主要目标就是几何研究,逐步建立起完整、科学的几何体系[2].
几何学所涉及的对象既与生活中的实物有关,又不完全等同于这些具体的实物[3].比如圆形、三角形、矩形等平面图形;球、圆柱、椎体、长方体等立体图形.现实生活中很少见到标准而且规范的图形,现实的实物应该是形似或神似的几何图形.因而几何图形是既普通又抽象的概念.每个平面图形的线、角、面等之间的关系;立体图形各个方位之间的关系;各个图形之间的关系都是深深吸引欧几里得的地方.
1 《几何原本》的公理化思想
欧几里得当时面临着两方面的问题,一方面,随着古希腊社会经济的繁荣和发展,特别是农林畜牧业的发展,土地的开发和利用日益增多,地形、地貌的研究需要广泛地应用几何学的知识.另一方面,前人积累了四百多年的几何知识,研究成果浩如烟海,随着探究的深入就会发现这些理论多是些海量又无序的片断.欧几里得意识到,如何把前人们留下的几何碎片知识进行梳理、论证和甄别,去伪存真,扬长避短,使这些几何学知识条理化和系统化,成为一整套可以自圆其说、前后贯通的知识体系,是完成既定目标的关键.
欧几里得的伟大贡献,在于使这些远古的数学思想与他个人的智慧完美结合起来,创立了欧几里得几何学体系.具体体现在他对《几何原本》的编排和大纲的制订,也就是公理化体系的建立.欧几里得的公理化思想的脉络是这样的:所有几何学的众多定理和结论都是建立在一些已知的结论基础上,经过严密的逻辑推理、演绎出来的.而这些已知的结论又是靠更基础的结论作基础,推理、演绎出来.也就是说每个定理和结论在通过一层层的推理过程中,都需要一个或几个最基础的理论作为理论支撑,这些最基础的结论显而易见、又无需证明.欧几里得把这些最基础的结论称作公理(适于数学的各学科)或公设(适于几何学).[4]按照这样的结构体系,欧几里德在《几何原本》卷首提出了五条公理、五条公设,并在各卷开头给出了一些定义(共二十三个).然后根据这些公理、公设、定义用严格的逻辑推论方法推导出了多达四百六十五个命题,把它们分门别类地组成了全文一十三卷,各卷的开头部分基本上都是从几何图形开始.纵观欧几里得在《几何原本》的编排过程,其公理化系统之严谨,逻辑推理之严密,令人叹为观止.
《几何原本》在卷首列出的五个公理为[4]:(1)等于同量的量彼此相等.即:如果A=C,B=C.则A=B;(2)等量加等量,其和相等.即:如果A=B,C=D.则A+C=B+D;(3)等量减等量,其差相等.即:如果A=B,C=D.则A-C=B-D;(4)彼此能重合的物体是相等的,如图1;(5)整体大于部分,如图2.
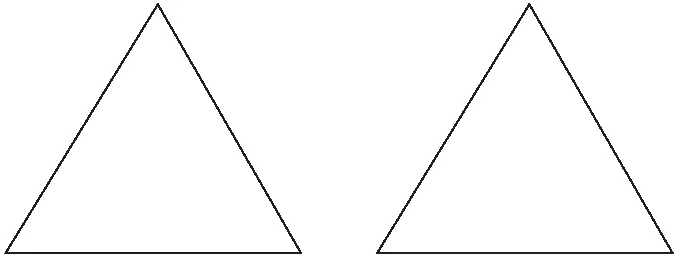
图1 彼此能重合的物体是相等的
五个公设为:(1)由任意点到任意另一点可作直线;(2)一条有限直线可以继续延长;(3)以任意点为圆心及任意距离为半径可以画圆;(4)凡直角都相等,如图3;(5)平面内一条直线与另外两条直线相交,若在直线同侧的两个内角之和小于180°,那么这两条直线无限延长后,在这一侧一定相交.如图4(∠1+∠2<180°).
这些公理、公设是初等数学的基础.可以说《几何原本》是两千多年来传播初等数学、几何知识的标准教科书.
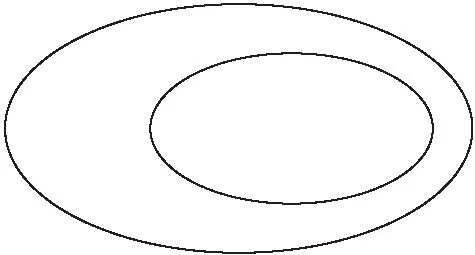
图2 整体大于部分

图3 凡直角都相等
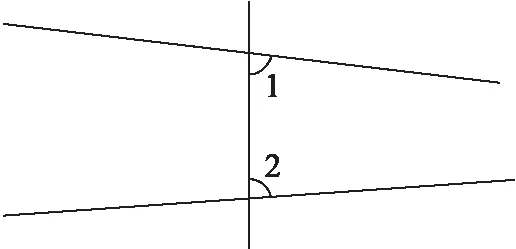
图4 两条直线无限延长后,在这一侧一定相交
2 我国几何学的公理化体系
《几何原本》不仅仅包括几何学知识,甚至包括初等数学的全部内容以及高等数学极限概念的雏形.内容涉及代数、数论、平面几何和立体几何的各个领域.
《几何原本》第一卷讲直线形,包括点、线、面、角的概念,三角形、两条直线的平行与垂直、勾股定理等.我们七年级几何学的就是三角形知识,两条直线的平行与相交.《几何原本》第二卷讲代数恒等式,如二项和的平方、黄金分割等.我们七年级代数知识的数、式的运算就是这一卷的内容.《几何原本》第三卷讲圆、弦、切线等与圆有关的图形.第四卷讲圆的内接、外切三角形、外接正方形、正多边形.我们八年级几何学的关于圆、圆的切线、圆与圆的位置关系、圆的内接、外切三角形等等就是这两卷的内容.《几何原本》第五卷讲比例论,第六卷将比例论应用于平面图形,研究相似多边形.我们八年级几何学是以相似三角形为主的相似图形,九年级几何是以四边形为主要内容的多边形知识[5].
以上我们把《几何原本》的基本内容与我国现阶段的初等数学内容作对比,就能发现我国初中阶段(七年级至九年级)数学知识主要取材于《几何原本》的前六卷.我国高中阶段的数学内容,则取材于《几何原本》后面几卷.不仅仅在数学课程上完全是《几何原本》的内容,我们数学的理论体系也完全是欧几里得《几何原本》的公理化体系[5].
我们高中阶段的立体几何[6],开宗明义的讲是建立在四个公理以及三个推论基础上.如著名的公理3:“经过不在一条直线上的三个点,有且只有一个平面”.不仅是确定一个平面的依据,是判定若干个点共面的依据;而且利用此公理还可以得到三个重要推论,每一个推论都具有不亚于公理的价值.如推论1:“经过一条直线和这条直线外一点,有且仅有一个平面”.成为判定若干条直线共面的依据; 判断若干个平面重合的依据; 判断几何图形是平面图形的依据.就这样,建立在公理(以及推论)基础上的判定定理、性质定理,构建起了立体几何的雄伟大厦.
3 结论
欧几里得《几何原本》对人们逻辑思维的锻炼,超过了亚里士多德的任何一篇逻辑论文,是严谨的逻辑推理体系的杰作.《几何原本》的公理化体系,也带动了现代科学的崛起,因为现代科学一部分是经验论和和实验法相结合的产物,另一部分是认真分析和逻辑演绎相结合的产物[7].
《几何原本》的公理化体系,成为用公理化方法建立起来的数学演绎体系的最早典范.这种公理法建立演绎体系的方法,在后来的二千多年间成为建立任何知识体系的严格方式,人们不仅应用于数学学科,也应用于其他科学领域,甚至应用于神学、哲学和伦理学,对后世产生了深远的影响.同时我们也能发现,有些公设的表述不够精准,比如公设3“有限直线”的提法就是错误的,因为直线是无限的.
吸收与扬弃并举,传承与创新并重.数学在进步,科学在进步,《几何原本》也在完善.
