改进型解耦控制的牵引网低频振荡抑制研究∗

张晓虎，邱鑫，肖伸平，孟江南，董翰林

（湖南工业大学电气与信息工程学院，湖南株洲412007）

0 引 言

随着我国电气化铁路的迅猛发展，新型交直交传动动车组与电力机车陆续投入使用，最近几年，我国电气化铁路牵引供电系统中频繁出现车网系统不匹配引发的低频振荡现象。目前网侧整流器（Line-Side Converter，LSC）广泛采用功率因数高、可控性好的单相脉冲整流器，普遍使用脉宽调制技术，且控制策略和控制参数对外部因素条件比较敏感，当LSC的控制参数和牵引网参数不匹配［1］时，就容易引发牵引网低频振荡问题。

目前，国内外对抑制牵引网低频振荡的方法主 要有文献［2］提出采用多变量控制来增强整流器抵抗振荡的能力，但变量之间容易相互影响而使控制性能变坏；文献［3］提出采用自抗扰控制（Active Disturbance Rejection Control，ADRC）来抑制高铁牵引网低频振荡，但该方法存在参数多且物理意义不明确，参数难整定等问题。文献［4］提出了一种基于二自由度内模控制的牵引网低频振荡抑制方法，可以实现良好的跟踪品质和鲁棒特性；但在系统对象与内部模型误差较大时，内模控制需要依靠滤波器系数的调整来整定控制器参数，这会降低系统的响应速度，牺牲系统的动态性能。

针对上述情况，本文采用dq解耦控制的策略，极大地降低了控制系统设计的复杂性，并具有良好的线性控制特性；再通过主动阻尼补偿方法，实现电流环的稳定跟踪，保证系统的稳定，从而有效抑制低频振荡。

1 牵引网低频振荡原因分析

由于低频振荡问题主要与列车的网侧变流器部分有关，考虑牵引供电系统阻抗的网侧变流器的等效电路如图1所示。

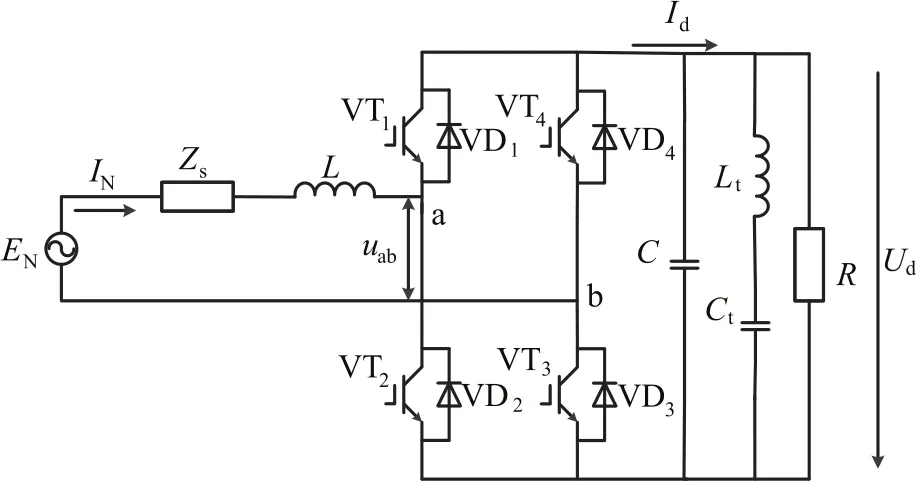
图1 网侧变流器等效电路图Fig．1 Equivalent circuit diagram of network side converter

EN为牵引变电所变压器电压折算到车载变压器的二次电压，假设其为理想电压源；Zs为牵引变压器阻抗与变电所到机车输入端的线路阻抗之和折算到车载变压器二次侧阻抗；L为牵引变电所变压器折算到车载变压器二次侧的感抗；R为机车直流侧等效负载；IN为网侧变流器的输入电流；uab为网侧变流器交流侧的电压；Ud为直流侧电压；Id为直流侧电流。

目前，牵引网中网侧变流器广泛采用双闭环的瞬态直流控制（Transient Current Control Strategy，TCCS）策略［5-6］，网侧等效阻抗Zs的大小忽略不计，其控制框图如图2所示。

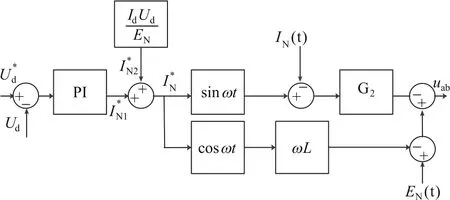
图2 基于双闭环PI控制器的TCCS框图Fig．2 Block diagram of TCCS based on double closed loop PI controller

其数学表达式为：

式中Id为直流侧电流；G2为电流放大系数；ω为网侧电压角频率。

假设同一地点同一供电区段同时接入n台同型号动车组，利用小增益定理，在赫尔维茨稳定判据的前提下，网侧变流器中间直流环节闭环控制系统的稳定条件［7］为：

式中U′d和I′N分别为线性化处理后的电压及电流静态直流分量。从式（5）可以看出，PI控制器的参数Kv，同时运行的动车组数量n，电感参数Ls、L，直流侧支撑电容C都会影响LSC直流侧输出电压稳定性。通常情况下发生低频振荡，通过调节 PI控制器参数Kv就可以使系统重新获得稳定，但当动车组数量变化导致系统无法满足赫尔维茨稳定判据时，此方法就不再适用。另外，由于LSC是一个非线性强耦合系统，对外界干扰和参数变化较为敏感，采用PI控制不易达到控制要求，故采用dq解耦的主动阻尼补偿控制方法。

2 dq解耦控制的原理

dq解耦控制方法，其核心思想是利用坐标系变换，将时变的交流量转化为直流量。通过采用前馈解耦的电流控制方法，完成了单相LSC有功功率与无功功率的独立解耦控制；同时在闭环控制中引入有功电流和无功电流有效值，实现了输入电流的无静差控制，降低了控制器对输入参数、网侧电压幅值等因素的敏感度。此外，本控制方法还可以实现变相位角控制，优化运行状态。

某车型单相网侧整流器解耦控制关系方程如下：

将式（7）～式（9）代入到式（6）中，解开微分项后，可得：

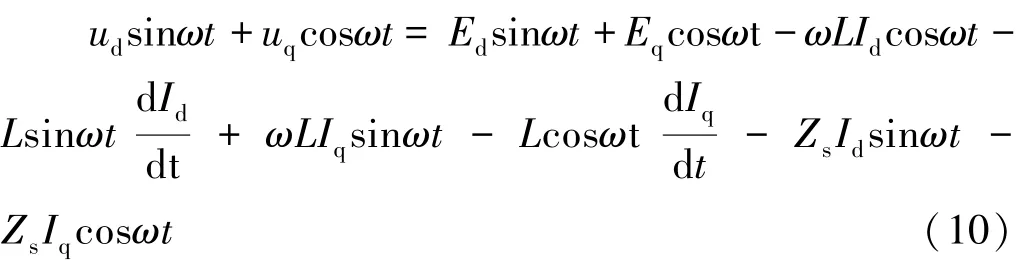
将sinωt项和cosωt项分别构成等式，可得：

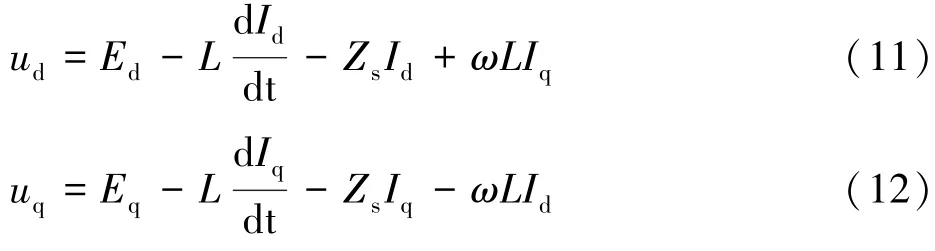
故网侧变流器的dq模型的矩阵形式描述为：

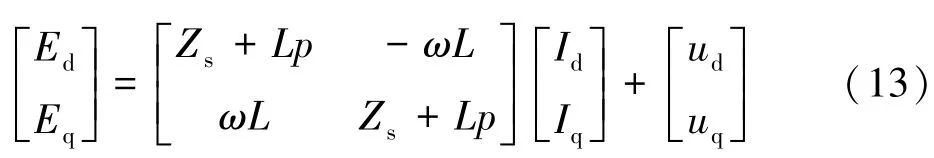
式（13）中，Ed、Eq为车载变压器的二次电压EN分解后的d，q分量；ud、uq为LSC输入侧电压uab分解后的d、q分量；Id、Iq为LSC输入侧电流IN的d、q分量；p是微分项。

设d轴与EN重合，则Eq=0。从式（13）可知，相互耦合的d，q轴变量对控制器的实现造成困难，故利用前馈解耦算法［8-9］，电流环采用PI控制，其ud、uq的控制方程为：

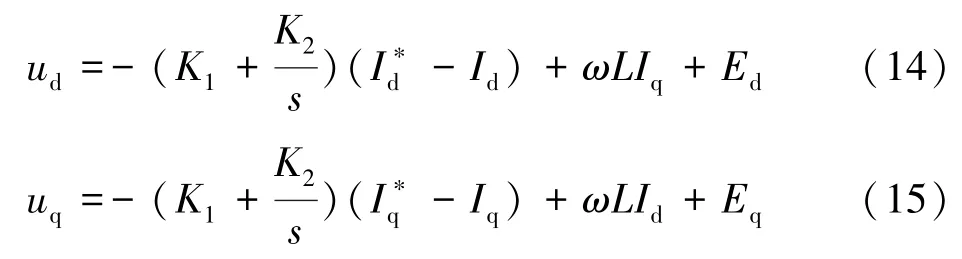
K1和K2分别为电流内环的比例和积分系数；I∗d、I∗为I、I的控制基准值。将式（14）和式（15）代入式qdq（13），得：

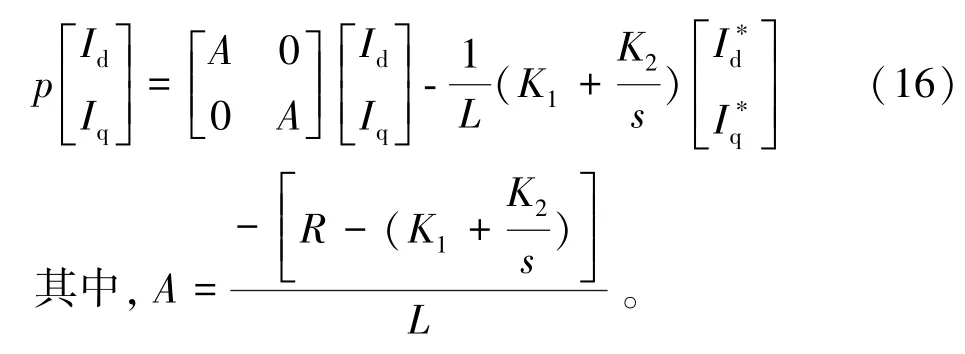
由式（16）可以看出，其解决了电流环dq分量间耦合的问题，消除了有功电流与无功电流的相互影响，且使电流环控制不依赖于PI控制器，实现网侧功率因数可控。当网侧电压下降严重时，引入容性无功电流，可适当提高网侧电压；当网侧电压过高时，引入感性无功电流，可适当降低网侧电压，保证系统的稳定。其控制框图如图3所示。

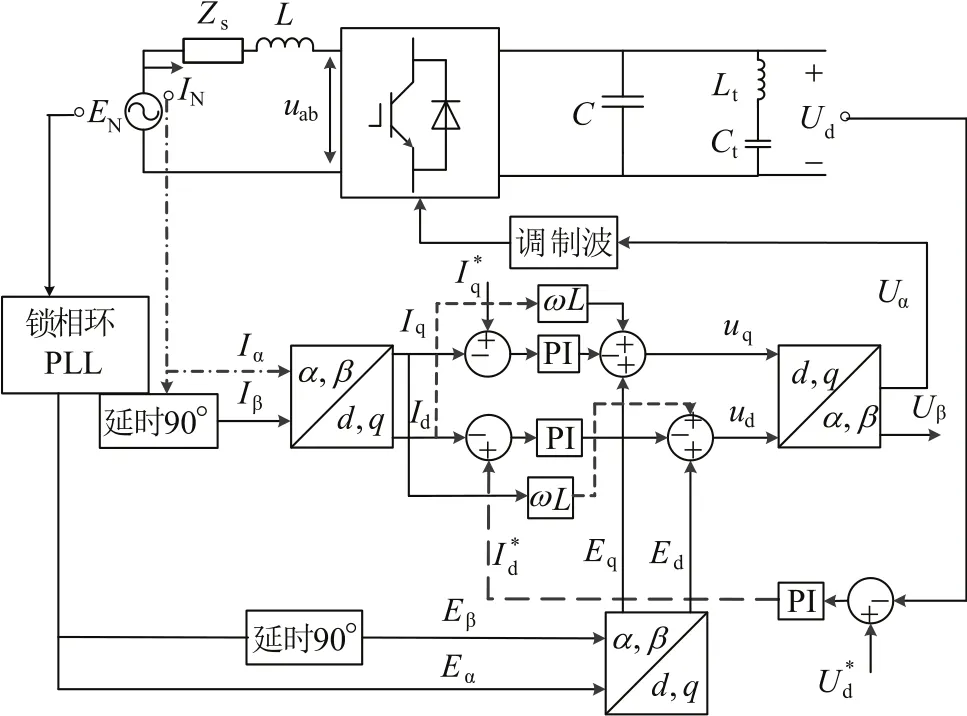
图3 基于dq解耦控制框图Fig．3 Block diagram based on dq decoupling control

3 主动阻尼补偿原理

无需阻尼电阻，通过改变控制器结构使系统稳定的控制策略称之为 “主动阻尼”［10-11］。通过将直流侧电压中的振荡分量反馈至电压环控制器后，采用主动阻尼补偿以增加系统阻尼，提高系统稳定性。

在系统平衡点附近通过线性化建立小信号模型［12-14］，电压环采用PI控制，Kp为电压外环控制器比例系数，τ为积分器时间常数。电流环近似为一阶惯性环节1／（ts+1），时间常数为t，可以将直流输出电压Ud的传递函数框图化简为如图4示形式。

图4 线性化得到的系统框图Fig．4 System block diagram obtained by linearization

参考国内某型车网侧变流器的主要电路参数，采用上述线性化后的控制模型，可求出系统阻尼比ε与振荡频率ω的表达式［12，15］，即：

其中

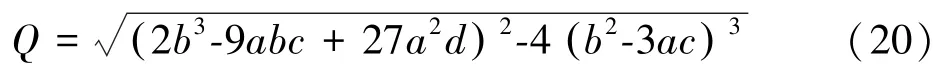
a，b，c，d为闭环系统特征多项式系数，系统极点分布图如图5所示。

由上述研究结果表明多车系统时，系统的阻尼比与系统主导极点位置密切相关［10，12，16-17］，振荡频率随控制环节变化。系统阻尼过小会造成系统低频振荡，适当的电压环设置可提高系统的稳定性，抑制低频振荡。

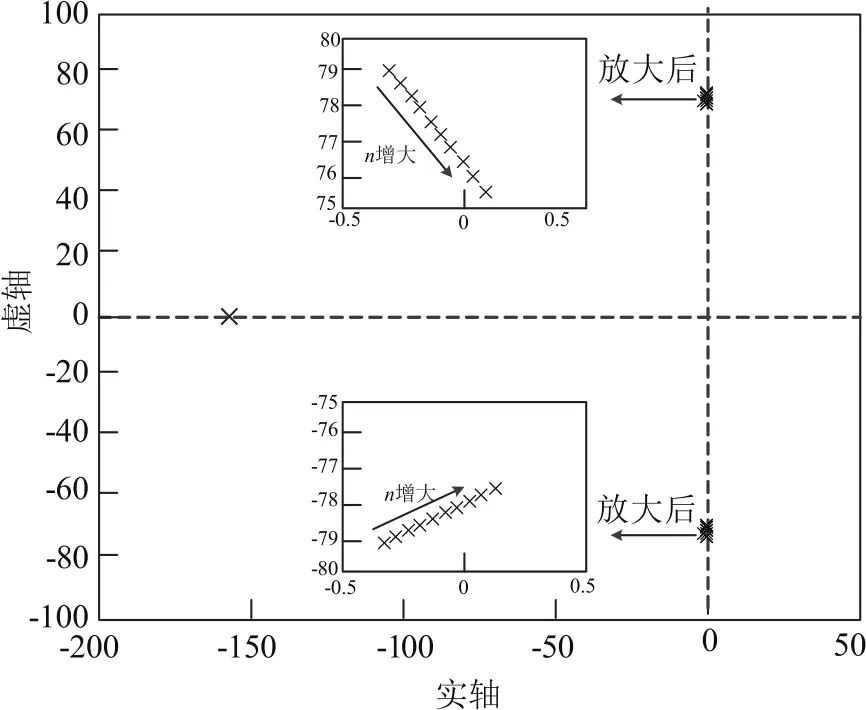
图5 系统极点分布图 （n=1，2…，10）Fig．5 System pole distribution diagram（n=1，2…，10）

由于低频振荡是由欠阻尼导致的，如果直流侧电压波动减小或者消失，网侧电压、电流会达到相位一致，系统也会恢复高功率因数运行。因此提出将直流侧电压信号反馈至电压环控制器后，通过二者做差来削弱振荡信号，实现系统稳定。其控制框图如图6所示。

图6 主动阻尼补偿的闭环系统框图Fig．6 Feed-back system block diagram with active damping compensation

加入主动阻尼补偿后，闭环系统直流侧电压振荡幅值较大程度地衰减，系统的带宽明显增大，动态响应速度变快，系统的抗干扰能力增强。理论分析表明，修正后的主动阻尼补偿系统，阻尼提高，稳定性更好。分析结果如图7所示。

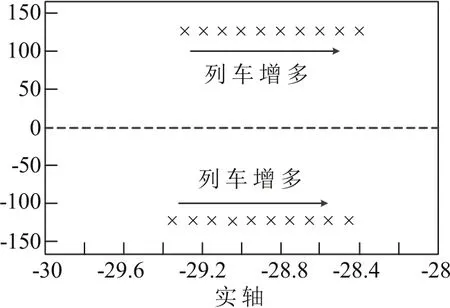
图7 加入主动阻尼补偿后系统主导极点分布图（n=1，2…，10）Fig．7 Dominant pole distribution of the system after adding active damping compensation （n=1，2…，10）

4 基于dq解耦的主动阻尼补偿控制

本文是通过dq解耦控制实现系统的线性化，再通过主动阻尼补偿策略消除直流侧电压的振荡分量，保证系统稳定，从而抑制低频振荡。其主要步骤如下：

（1）首先构建静止αβ坐标系，接着建立单相PWM整流器的dq同步旋转坐标系模型，控制系统的锁相环从网压过零点开始计算wt；

（2）将时变的交流量转化成直流量，实现对网侧输入电流的实时无静差控制。网侧电压经过同步旋转坐标系变换得到ud和uq分量，最后利用低通滤波避免将高频噪声引入VOC控制；

（3）采用前馈解耦电流控制算法，引入新的输入变量I∗d、I∗q，使得Id、Iq转化为解耦的线性关系，同时保证dq轴控制器能够独立地控制输入电流的 dq轴分量，实现对网侧输入电流波形与功率因数的控制；

（4）在不改变控制参数的前提下，在LSC控制中加入形如g／hs+1的补偿器，将直流侧电压取得的振荡信号反馈至PI控制器之后，增加阻尼。削弱直流侧电压振荡幅值，增强系统的稳定性。

5 仿真分析

为验证本文所提方法的有效性，在MATLAB环境中搭建了双重化LSC的仿真模型，如图8所示，仿真参数如表1所示。两重化整流器直流侧输出电压性能指标如表2所示。

对动车组LSC分别采用基于双闭环的瞬态直流控制和基于dq解耦的主动阻尼补偿控制方式，进行仿真分析，仿真结果如下所示，输出仿真波形见图9～图10。

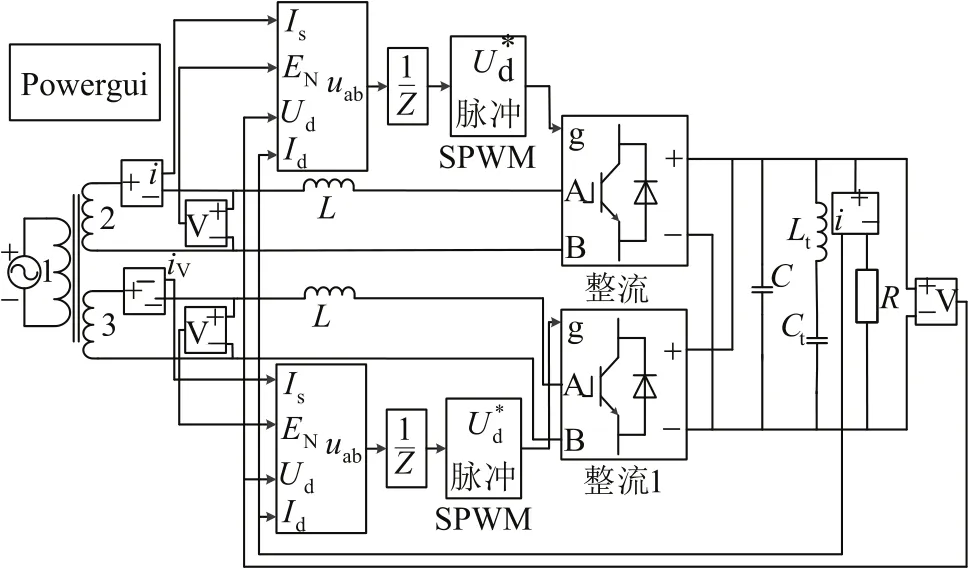
图8 基于双闭环瞬态直流控制的LSC建模Fig．8 LSC modeling based on double closed loop transient DC control

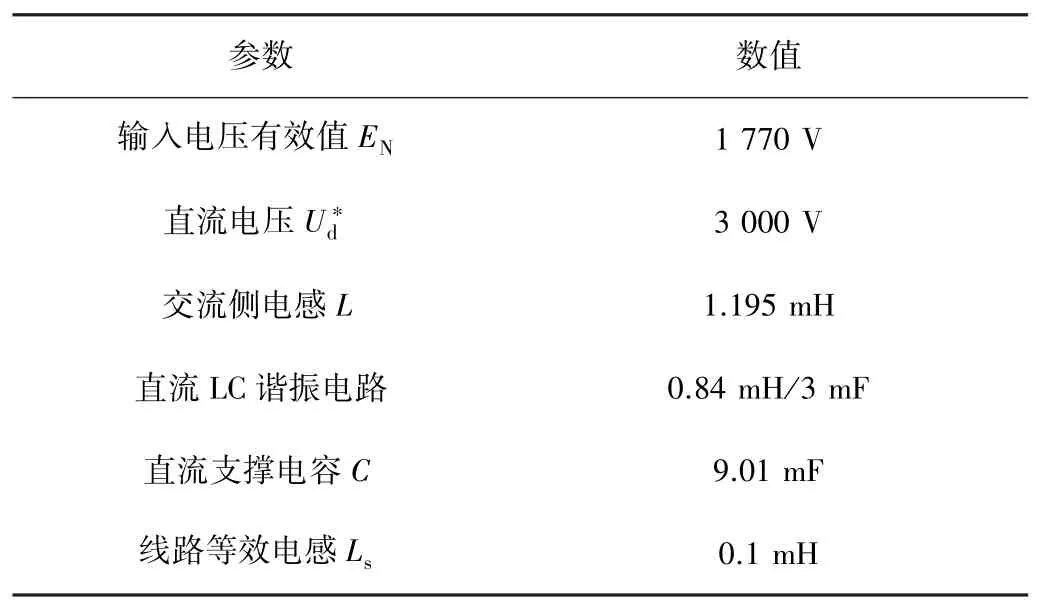
表1 整流器仿真参数Tab．1 Simutation parameters of rectifier

表2 两重化整流器直流侧输出电压性能指标Tab．2 Performance index of DC side output voltage of dual rectifier

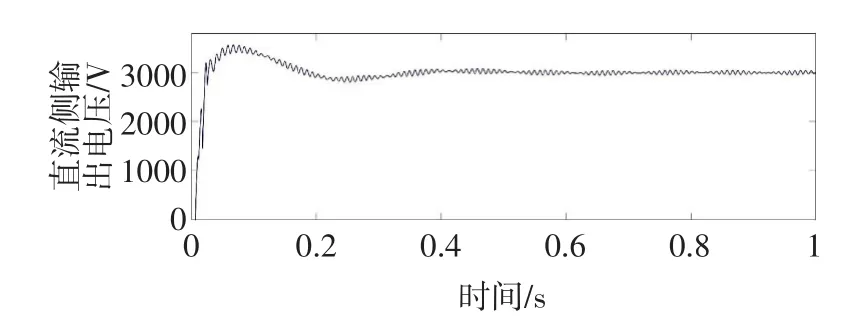
图9 基于双闭环的瞬态直流控制的LSC直流侧电压输出仿真波形Fig．9 Simulation waveform of LSC DC side voltage output based on double closed loop transient DC control

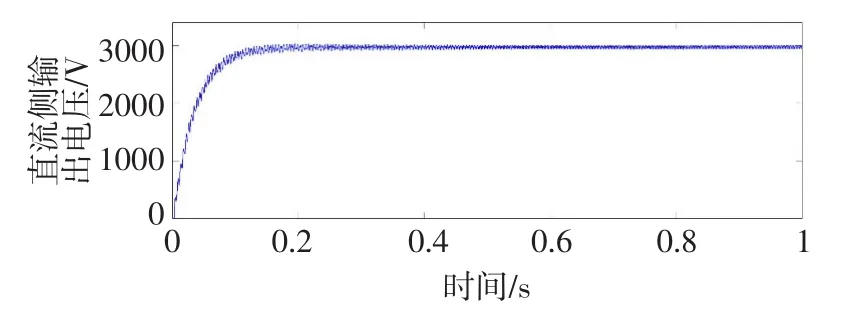
图10 基于dq解耦的主动阻尼补偿控制的LSC直流侧电压输出仿真波形Fig．10 Simulation waveform of LSC DC side voltage output based on dq decoupling active damping compensation control

对比图9和图10可知，2种控制方式下输入电流正弦度都较好，采用双闭环瞬态直流控制方式时 ，直流侧输出电压稳定过程中存在超调量，且输出波形波动较大，抗干扰能力较差；采用基于dq解耦的主动阻尼补偿控制方式时，没有出现超调量，直流侧电压振荡幅值较大程度地减少，动态响应速度有所提高，系统的抗干扰能力增强。表明基于dq解耦的主动阻尼补偿控制方式对低频振荡有较好的抑制效果。

6 结束语

本文针对牵引网低频振荡的抑制方法进行研究，提出了改进型的dq解耦主动阻尼补偿控制方式，搭建了LSC仿真模型，仿真结果证明了本文方法能够克服PI控制的超调和抗扰能力差的问题，具有更好的跟踪性能，更强的抗扰能力，同时通过系统仿真表明该方法对抑制牵引网低频振荡的有效性。