NEW PROOFS OF THE DECAY ESTIMATE WITH SHARP RATE OF THE GLOBAL WEAK SOLUTION OF THE n-DIMENSIONAL INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
2019-01-09LinghaiZhang
Linghai Zhang
(Dept.of Math.,Lehigh University,14 East Packer Avenue,Bethlehem,Pennsylvania 18015,USA)
Abstract Consider the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations:−α△u+(u·∇)u+∇p=f(x,t),with the initial condition u(x,0)=u0(x)and with the incompressible conditions∇ ·u=0,∇ ·f=0 and∇·u0=0.The spatial dimension n≥2.Suppose that the initial function u0∈L1(Rn)∩L2(Rn)and the external force f∈L1(Rn×R+)∩L1(R+,L2(Rn)).It is∫ well known that there holds the decay estimate with sharp rate:(1+t)1+n/2 Rn|u(x,t)|2dx≤C,for all time t>0,where the dimension n≥2,C>0 is a positive constant,independent of u and(x,t).The main purpose of this paper is to provide two independent proofs of the decay estimate with sharp rate,both are complete,systematic,simplified proofs,under a weaker condition on the external force.The ideas and methods introduced in this paper may have strong in fluence on the decay estimates with sharp rates of the global weak solutions or the global smooth solutions of similar equations,such as the n-dimensional magnetohydrodynamics equations,where the dimension n≥2.
Keywords n-dimensional incompressible Navier-Stokes equations;global weak solution;decay estimate with sharp rate;Fourier transformation;Parseval’s identity;Gronwall’s inequality
1 Introduction
1.1 The mathematical model equations
Consider the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations
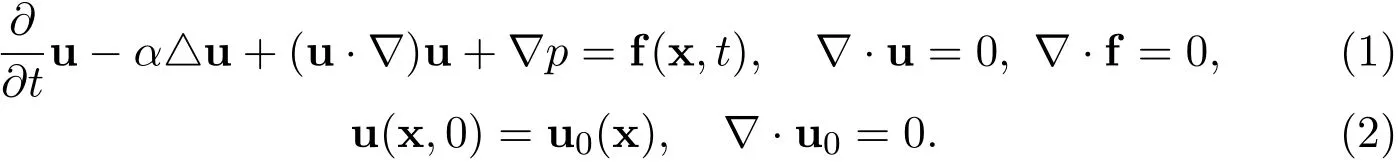
The real vector valued function u=u(x,t)represents the velocity of the fluid at position x and time t.The real scalar function p=p(x,t)represents the pressure of the fluid at x and t.The positive constant α>0 represents the diffusion coefficient.
1.2 Previous related results
The existence of a global weak solution or a global smooth solution:Suppose that the initial function u0∈L2(Rn)and the external force f∈L1(R+,L2(Rn)).Then there exists a global weak solution u∈L∞(R+,L2(Rn)),such that∇u∈L2(R+,L2(Rn)).Moreover,for the spatial dimension n=2,if the initial function u0∈L1(R2)∩H2m+1(R2)and the external force f∈L1(R2×R+)∩L1(R+,L2(R2))∩L2(R+,H2m(R2)),then there exists a global smooth solution u∈L∞(R+,H2m+1(R2)),such that∇u∈L2(R+,H2m+1(R2)),for any positive integer m≥1.Under additional conditions,the solution is in finitely smooth:u∈C∞(R2×R+).There holds the following solution representation
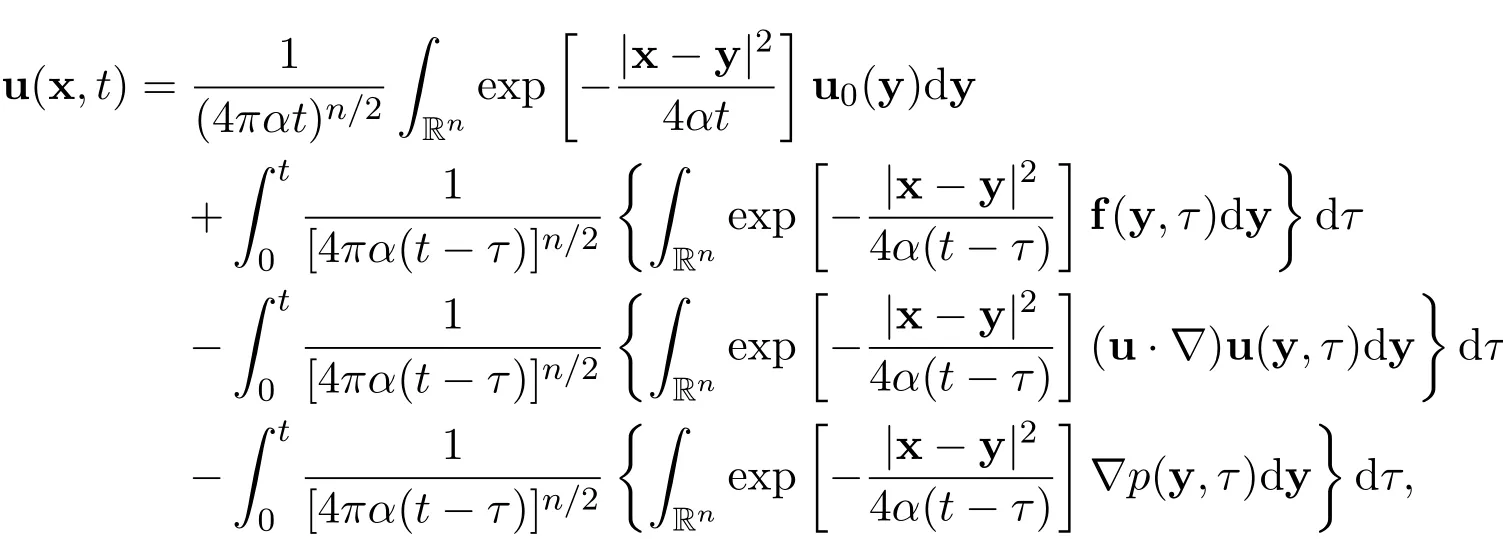
where

for all x∈Rnand t>0.
The decay estimates with sharp rates:Suppose that the initial function u0∈L1(Rn)∩L2(Rn)and the external force f∈L1(Rn×R+)∩L1(R+,L2(Rn)).Then there holds the following decay estimate with sharp rate

for all t>0,where C>0 is a positive constant,independent of u and(x,t).
1.3 The mathematical assumptions
Suppose that the initial function u0∈L1(Rn)∩L2(Rn)and the external force f∈L1(Rn×R+)∩L1(R+,L2(Rn)).Suppose that there exist real scalar functions ϕkl∈ C1(Rn)∩L1(Rn)and ψkl∈ C1(Rn× R+)∩L1(Rn×R+),such that
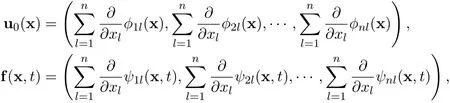
and that
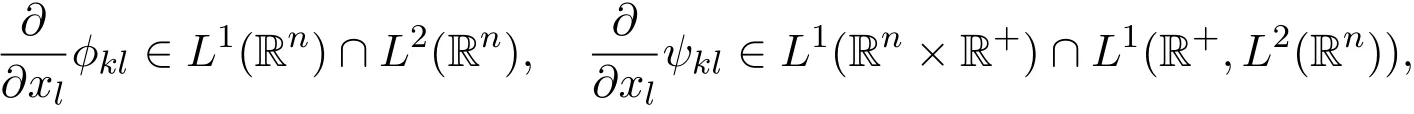
for all positive integers k=1,2,3,···,n and l=1,2,3,···,n.
These assumptions are motivated by the special structures of the nonlinear functions(u·∇)u and∇p in the n-dimensional incompressible Navier-Stokes equations,due to the incompressible condition∇·u=0.They are also motivated by the following facts
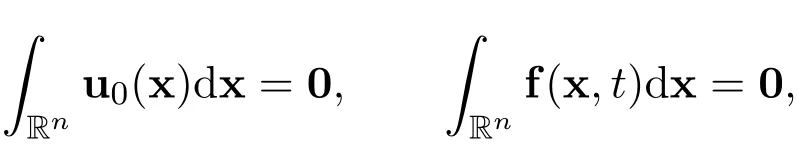
for all t>0.
Suppose that there exists the following integral
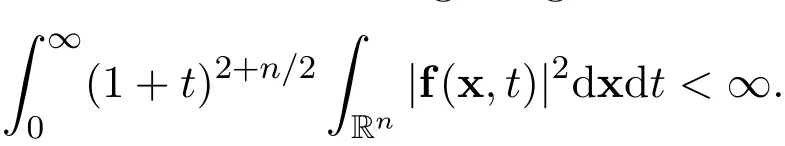
We allow the initial function and the external force to have some lower order singularity,such as
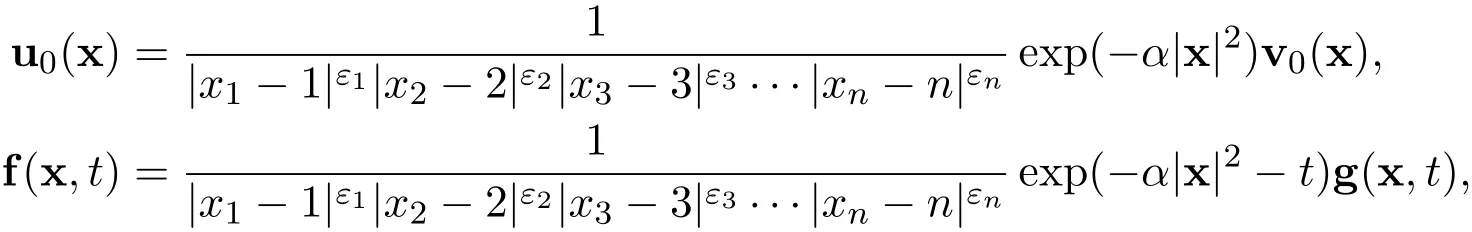
where ε1, ε2, ε3, ···, εnare sufficiently small positive constants,such that 0<2ε1<1,0<2ε2<1,0<2ε3<1,···,0<2εn<1.The functions v0=v0(x)and g=g(x,t)are chosen in such a way that∇·u0=0 and ∇·f=0.
1.4 The main results
There holds the following decay estimate with sharp rate for the global weak solution of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations(1)-(2):
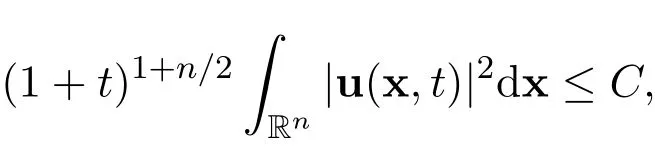
for all time t>0,where the dimension n≥2,C>0 is a positive constant,independent of u and(x,t).
2 The Mathematical Analysis and the Proofs of the Main Result
For the decay estimate with sharp rate of the global weak solution of(1)-(2),we will provide two independent proofs:one proof for the case n≥2 and another proof for the case n≥3.Both proofs are complete,systematic and simpler than before.
2.1 The proof of the decay estimate with sharp rate for the case n≥2
We will provide the proof of the decay estimate with sharp rate for the global weak solution of(1)-(2),where the dimension n≥2.
Theorem 1Suppose that the initial functionu0∈L1(Rn)∩L2(Rn)and the external forcef∈L1(Rn×R+)∩L1(R+,L2(Rn)).Suppose that there exists the following integral
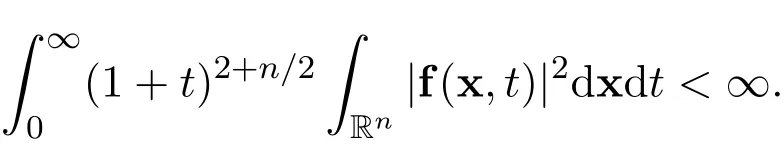
Then there holds the following decay estimate with sharp rate

for all timet>0,where the dimensionn≥2,C>0is a positive constant,independent ofuand(x,t).
Proof There are three main steps in the proof of Theorem 1.
Step 1The proof of the elementary decay estimate
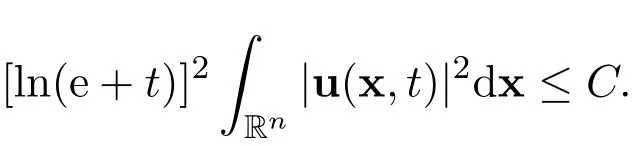
Multiplying the n-dimensional incompressible Navier-Stokes equations by 2u and integrating the result with respect to x over Rnyield

where
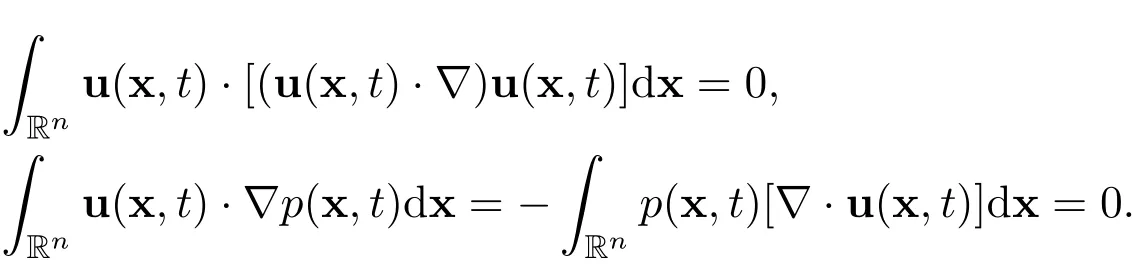
Applying the Parseval’s identity to the last energy equation leads to
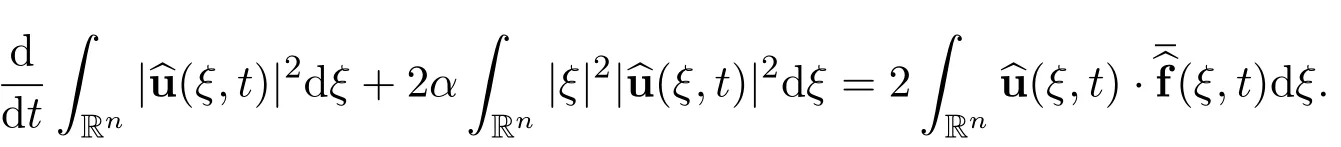
Multiplying this equation by[ln(e+t)]2ngives the new energy equation
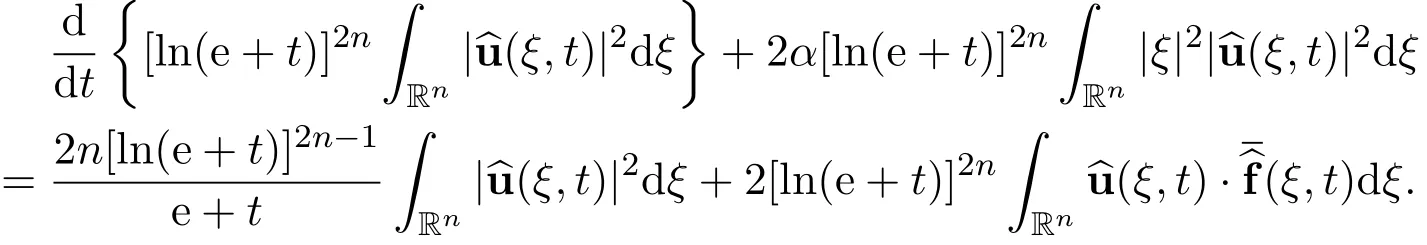
By using Cauchy-Schwartz inequality,we have the following estimate
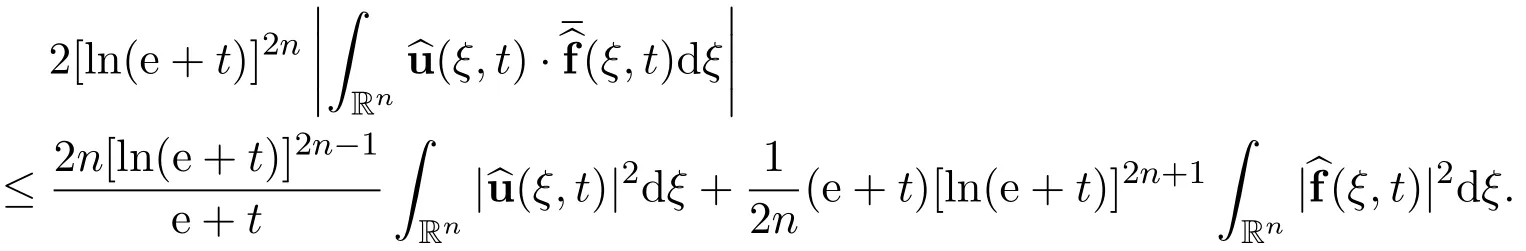
Therefore,the above energy equation becomes the differential inequality
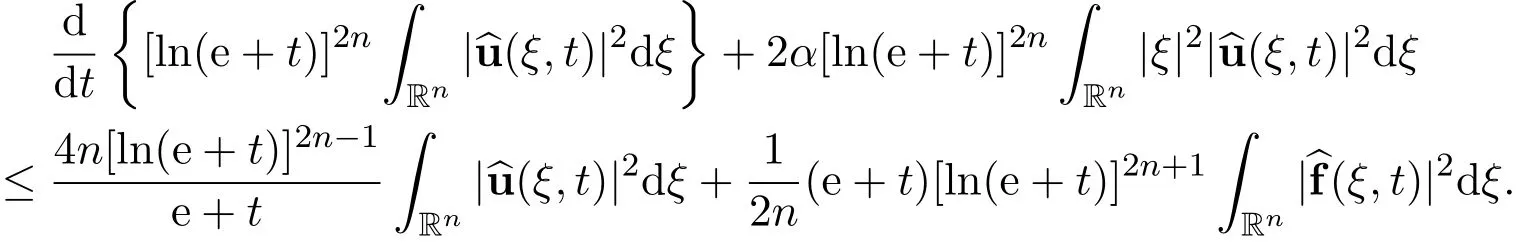
Let us split the frequency space as the union of a small ball and its complementary.Define
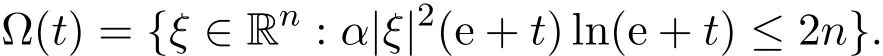
Then there hold the following estimates

Therefore,the above differential inequality reduces
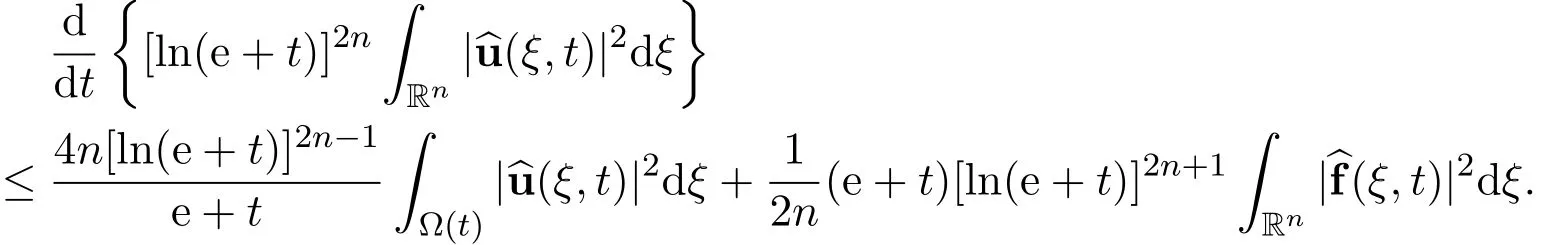
Applications of standard ideas and methods in differential equations lead to the following representation of the Fourier transformation

Note that
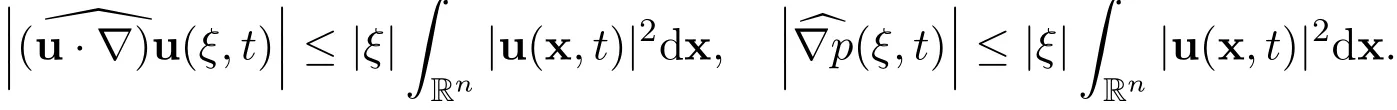
Now we have
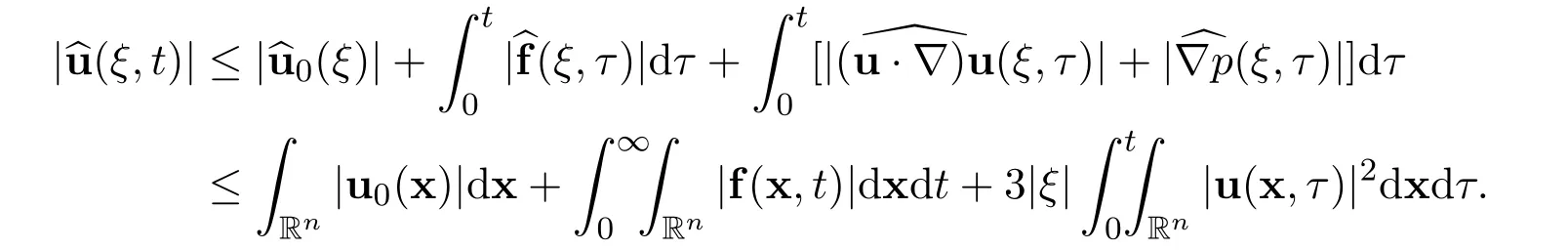
Multiplying the n-dimensional incompressible Navier-Stokes equations(1)by 2u and integrating the result with respect to x over Rn,using Cauchy-Schwartz’s inequality and integrating the differential inequality with respect to time t leads to the following elementary uniform energy estimate
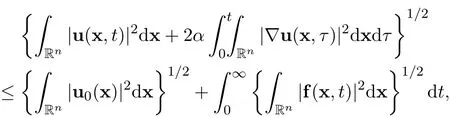
for all t>0.
Therefore,there hold the following estimates
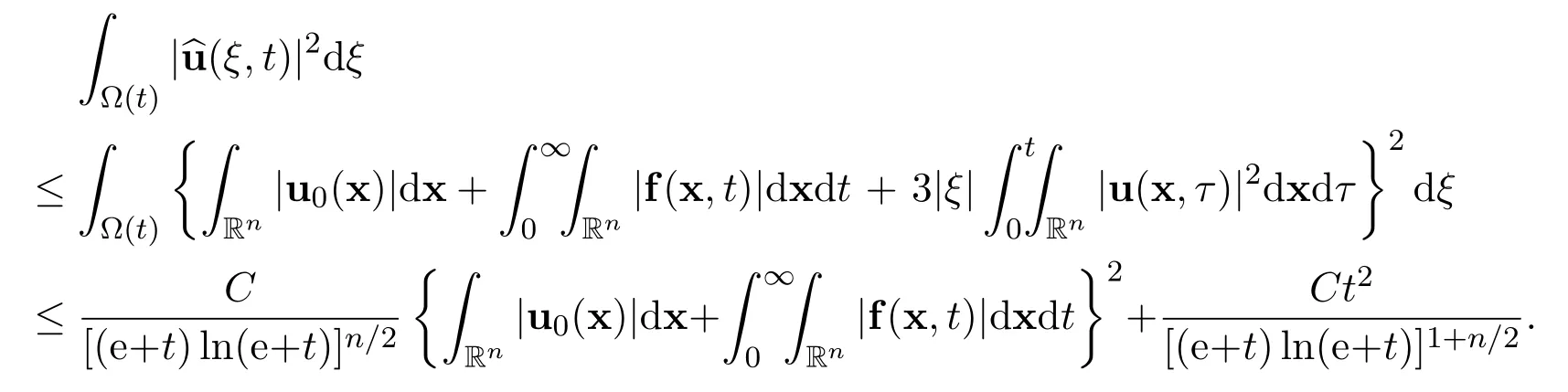
Now the above differential inequality becomes
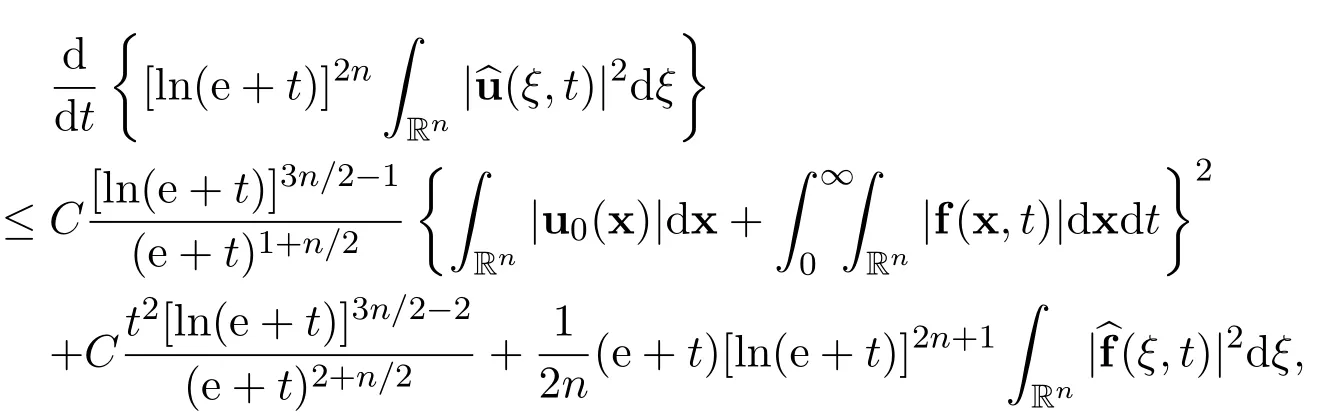
where C>0 is a positive constant,independent of u and(x,t).Integrating the inequality with respect to time t leads to

Therefore,there holds the following elementary decay estimate
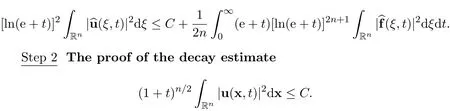
Multiplying the n-dimensional incompressible Navier-Stoke equations by 2u and integrating the result with respect to x over Rnyield

where
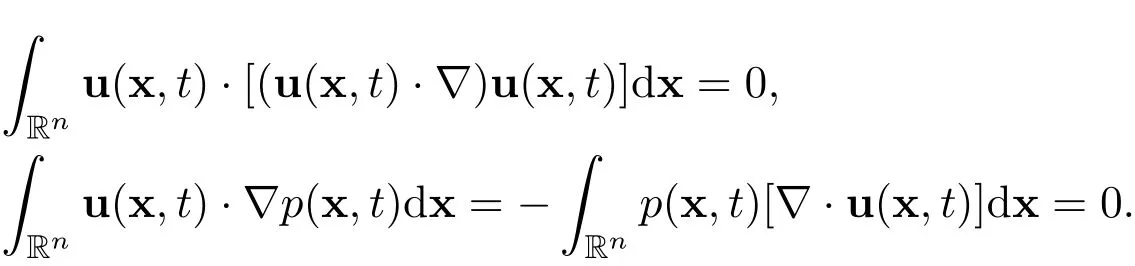
Applying the Parseval’s identity to the energy equation leads to

Multiplying this equation by(1+t)2n,we get

By using Cauchy-Schwartz’s inequality,we have
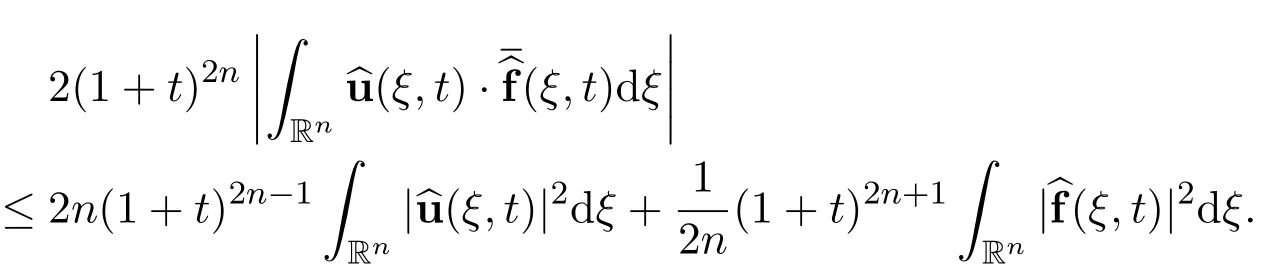
Now the above energy equation becomes a differential inequality

Define
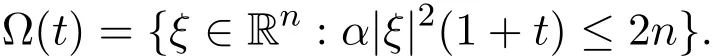
Then there hold the following estimates

Now the differential inequality reduces
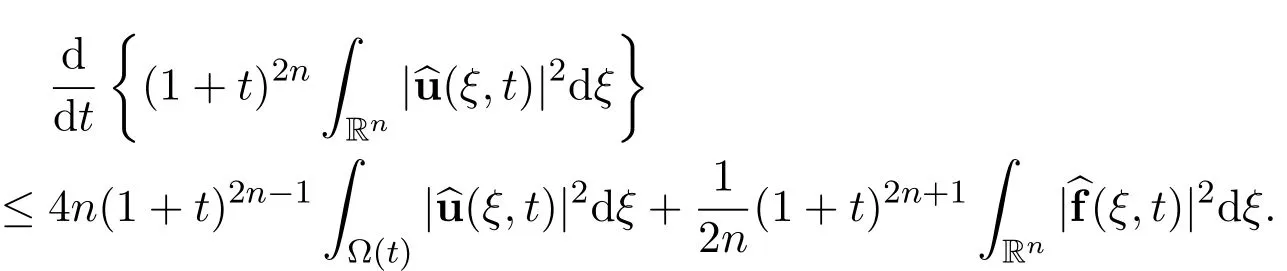
By using the representation of the Fourier transformation
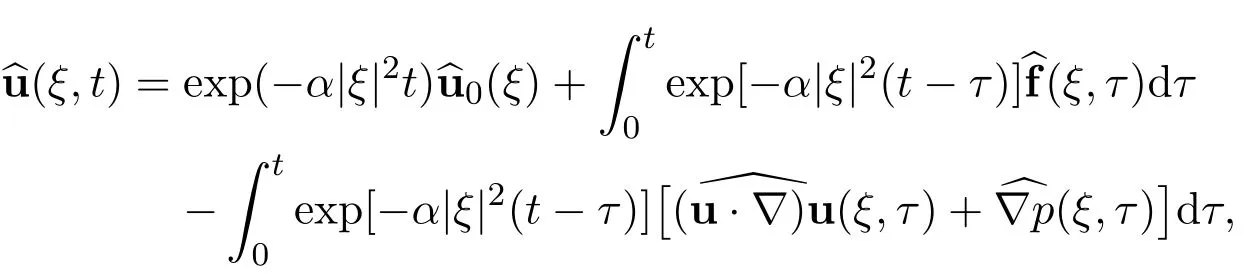
we have the estimate
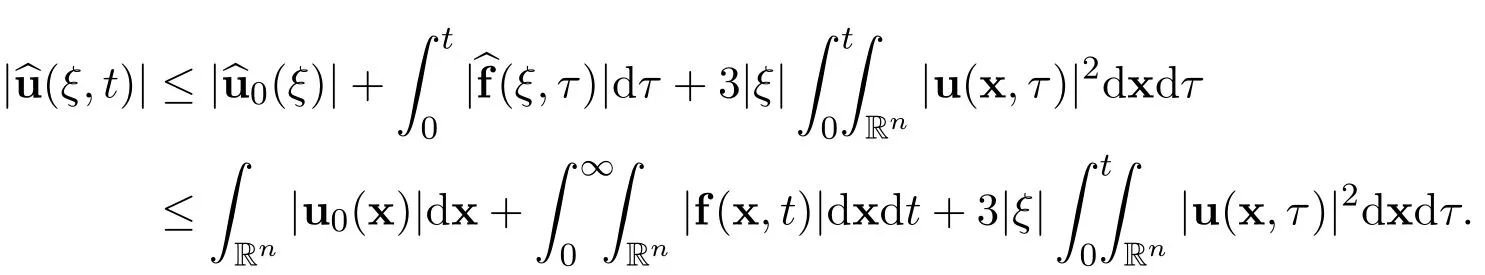
Now there hold the following estimates
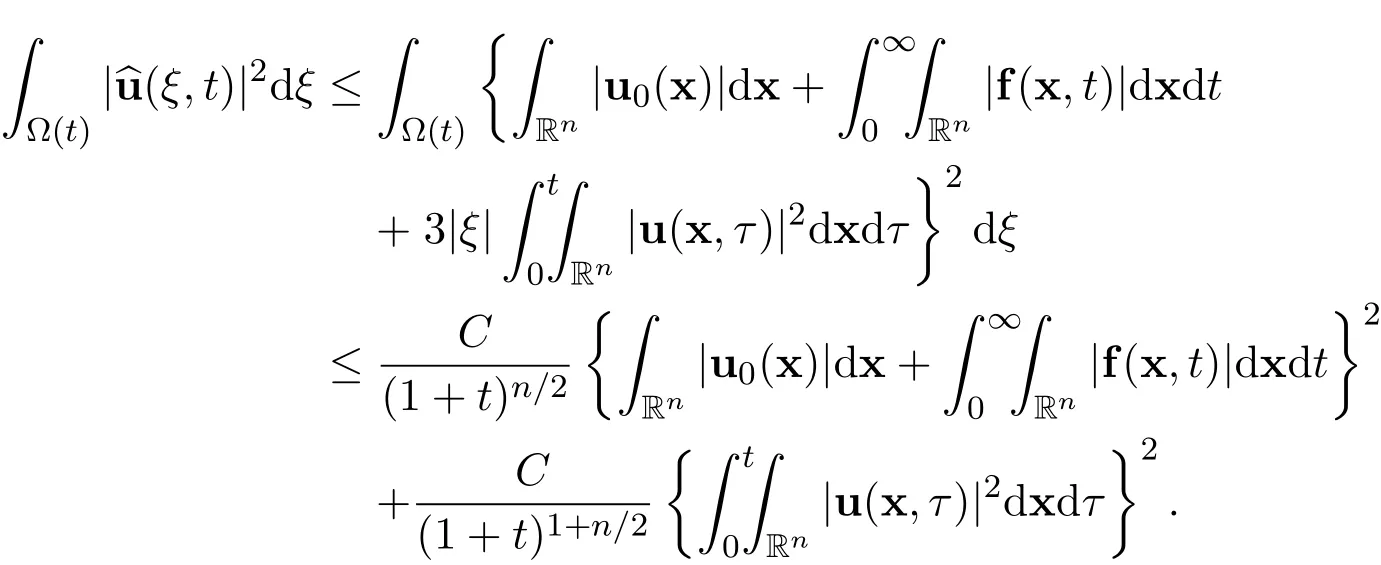
Therefore,we have the following inequality
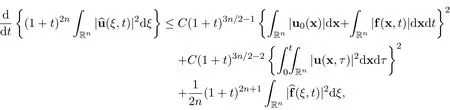
where C>0 is a positive constant,independent of u and(x,t).Integrating this inequality with respect to time t yields

That is
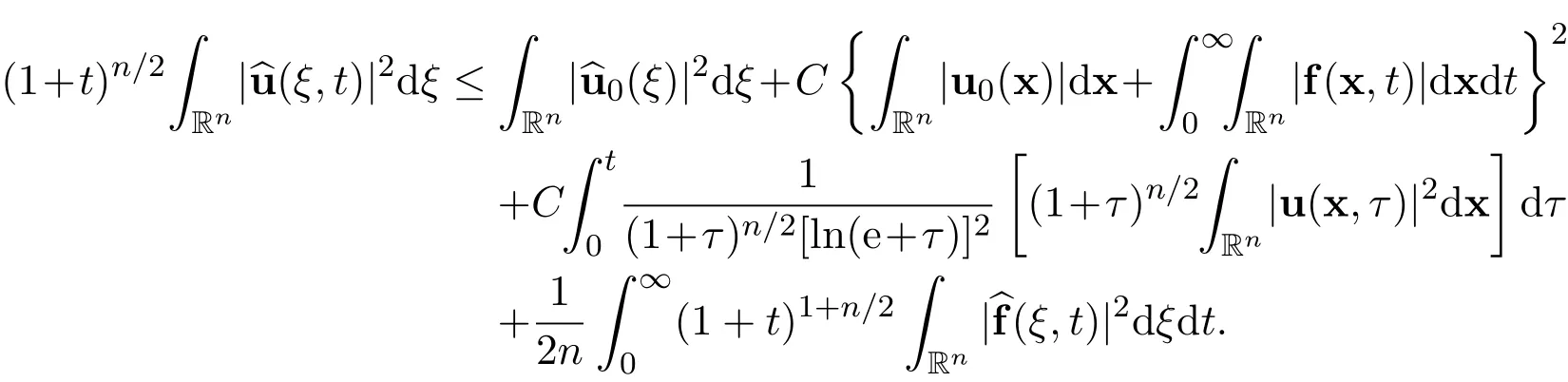
By using Gronwall’s inequality,we obtain the decay estimate

where C>0 is a positive constant,independent of u and(x,t).
Step 3The proof of the decay estimate with sharp rate
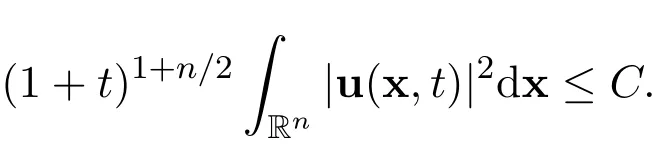
Recall that we have derived the representation for the Fourier transformation

Suppose that there exist real scalar functions ϕkl∈ C1(Rn)∩ L1(Rn)and ψkl∈C1(Rn× R+)∩ L1(Rn× R+),for all k=1,2,3,···,n and l=1,2,3,···,n,such that
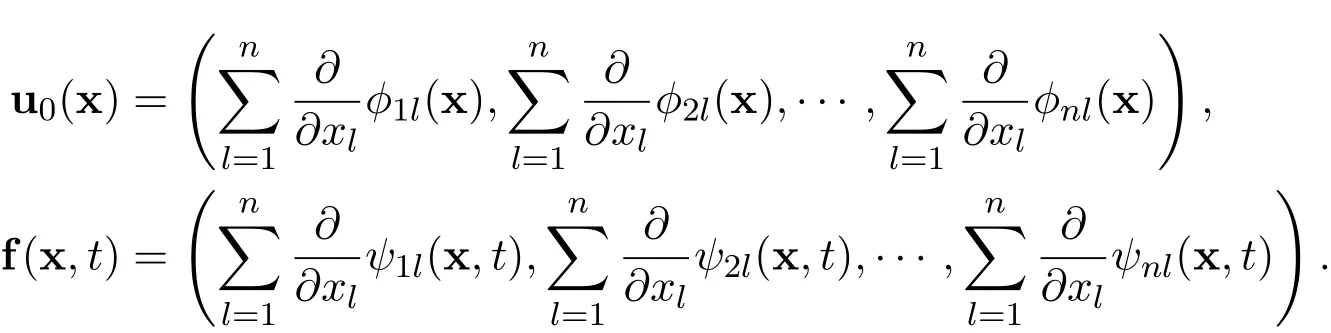
Performing Fourier transformation to the initial function and the external force yields the following representation
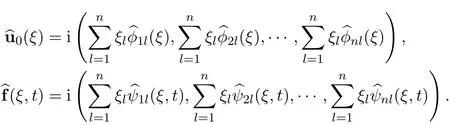
The following estimates follow from the Cauchy-Schwartz’s inequality
Therefore
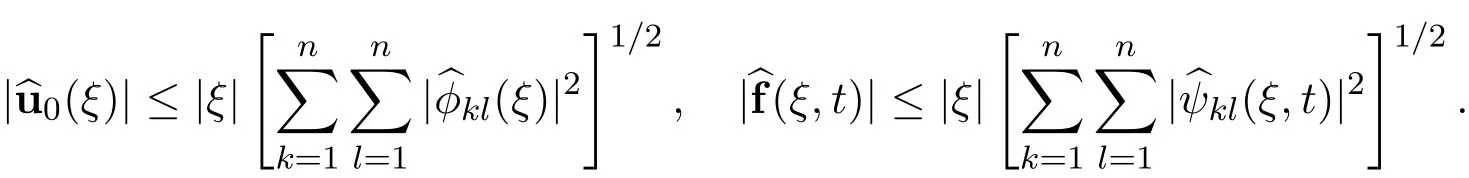
Taking the divergence of the n-dimensional incompressible Navier-Stokes equations leads to
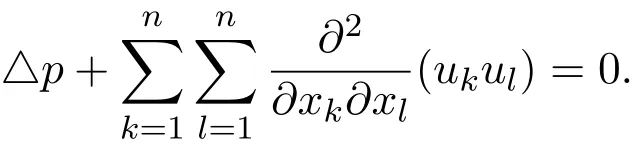
Performing the Fourier transformation to this equation yields
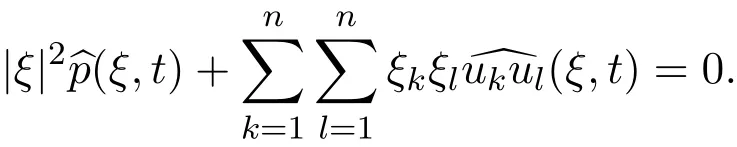
By using the Cauchy-Schwartz’s inequality,we can easily establish the following estimates
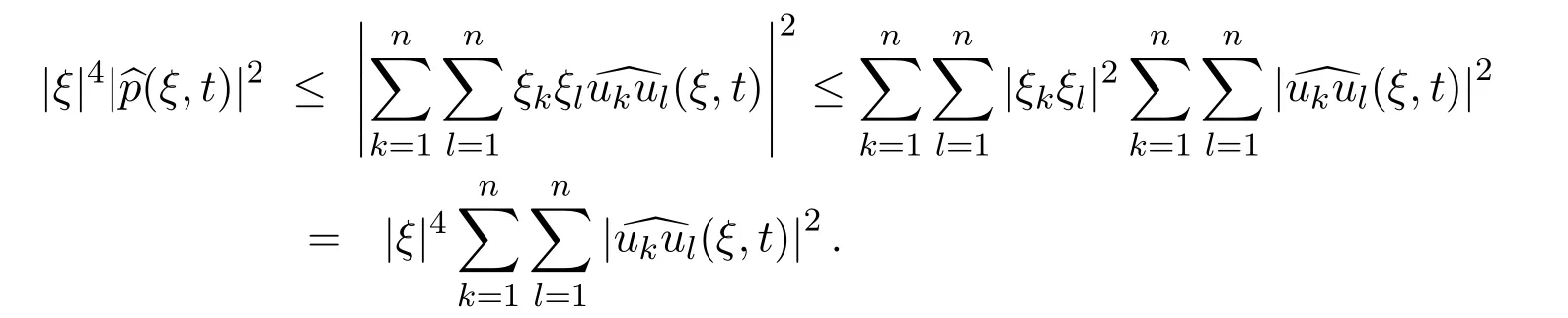
Therefore
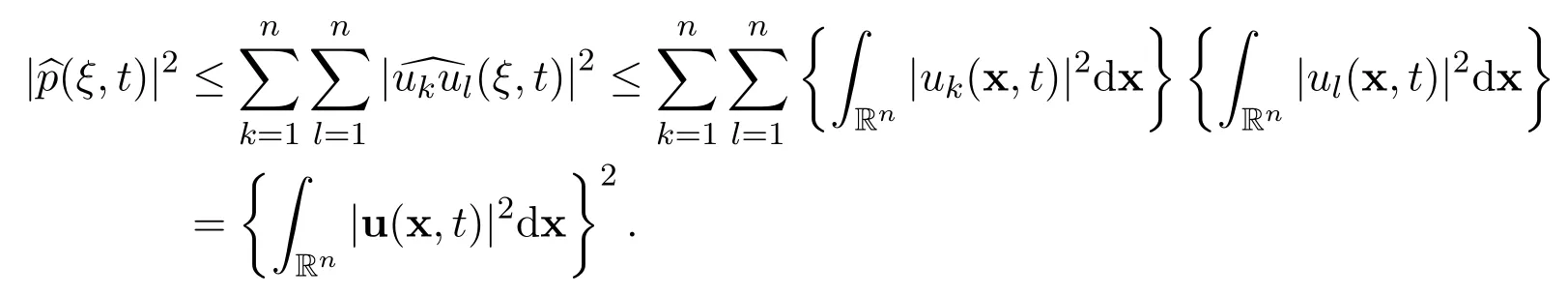
Now there hold the following estimates
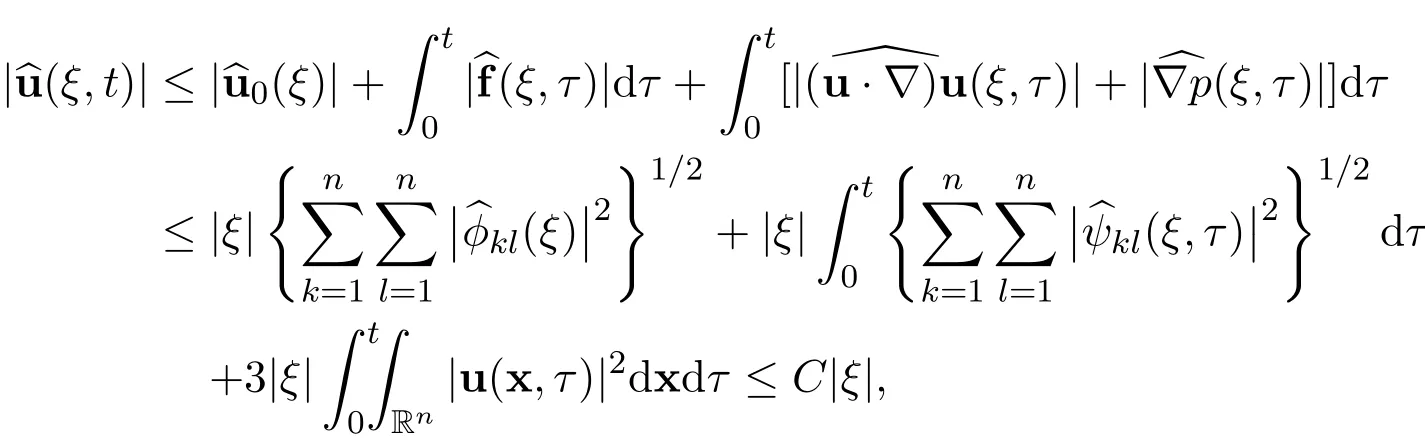
and then
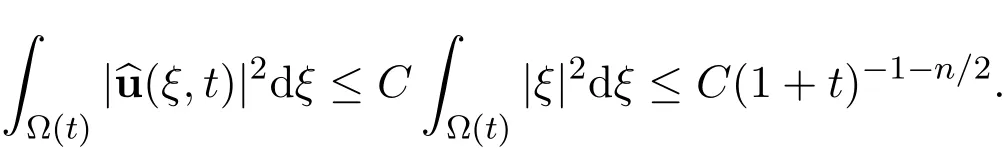
Therefore
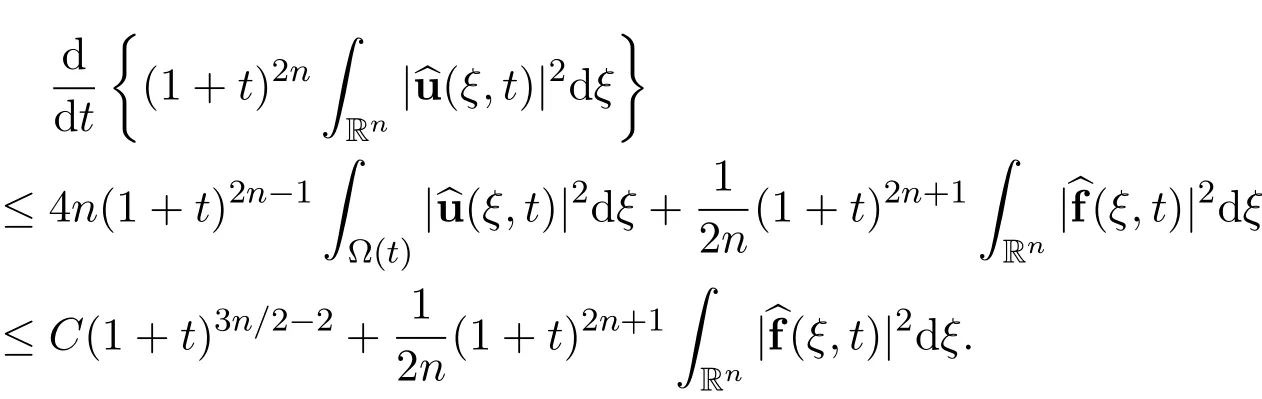
Upon integrating this inequality with respect to time t,there hold the following estimates

Finally
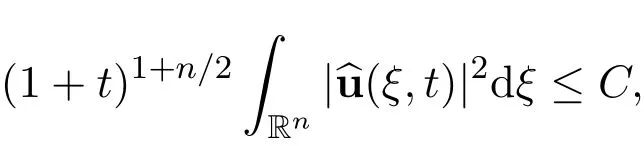
where C>0 is a positive constant,independent of u and(x,t).
The proof of Theorem 1 is completed finished.
Remark 1 For the two-dimensional incompressible Navier-Stokes equations
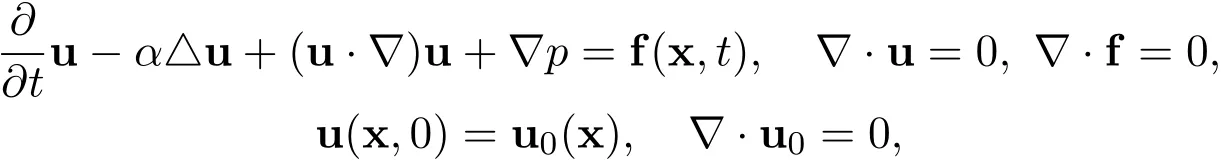
where
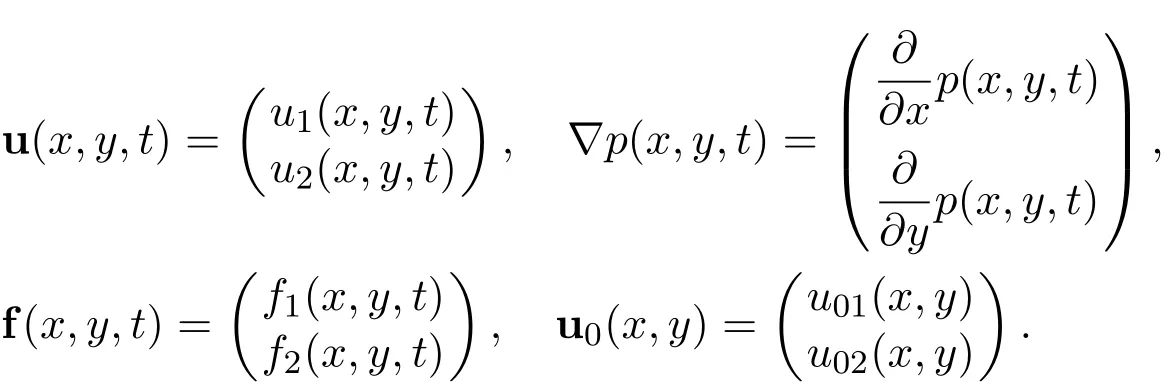
Let
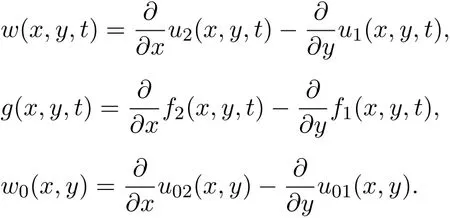
Then
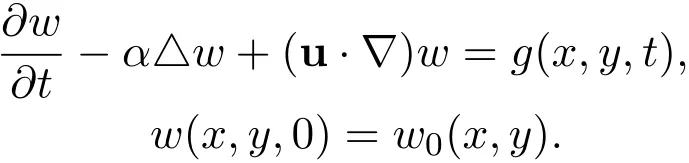
Multiplying this equation by 2w and integrating the result with respect to(x,y)over R2leads to
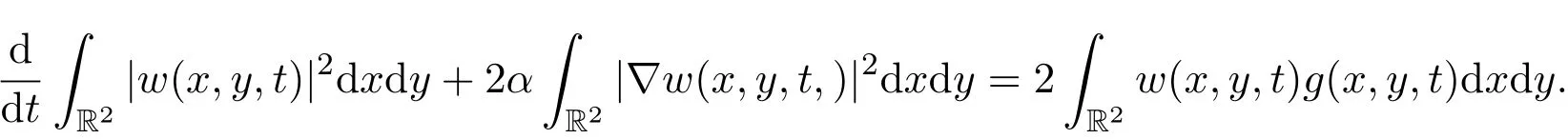
That is
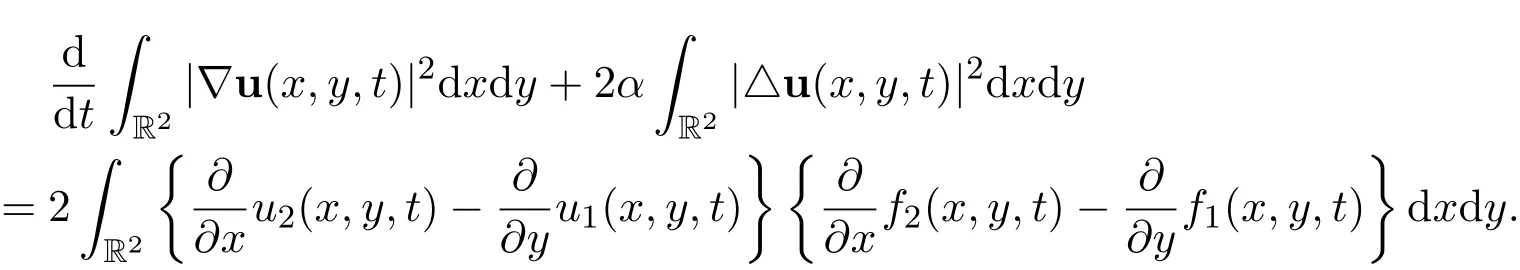
Then we may use very similar ideas to establish the decay estimate with sharp rate.For higher order derivatives of the global smooth solution,we may use very similar ideas to establish the decay estimates with sharp rates,provided that there hold the corresponding uniform energy estimates for the derivatives.
2.2 The proof of the decay estimate with sharp rate for the case n≥3
The proof of the decay estimate with sharp rate of the global weak solution of the case n≥3 is independent of the proof of the case n≥2.
Theorem 2Suppose that the initial functionu0∈L1(Rn)∩L2(Rn)and the external forcef∈L1(Rn×R+)∩L1(R+,L2(Rn)).Suppose that there exists the following integral
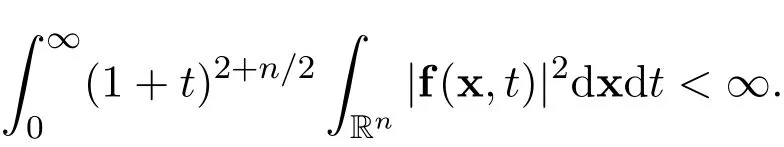
Then there holds the following decay estimate with sharp rate

for allt>0,where the dimensionn≥3,C>0is a positive constant,independent ofuand(x,t).
Proof There are twelve simple steps in the proof.
Step 1A differential inequality.Multiplying the n-dimensional incompressible Navier-Stokes equations(1)by 2u and integrating the result with respect to x over Rnyields the energy equation
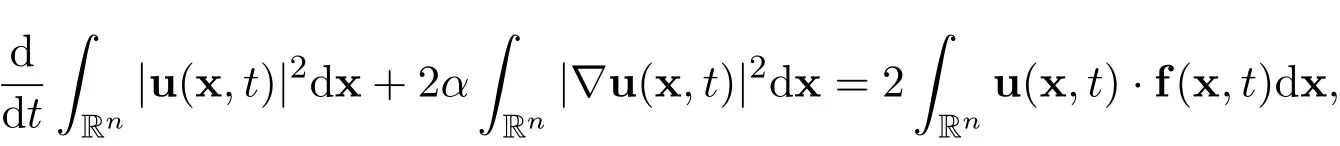
where
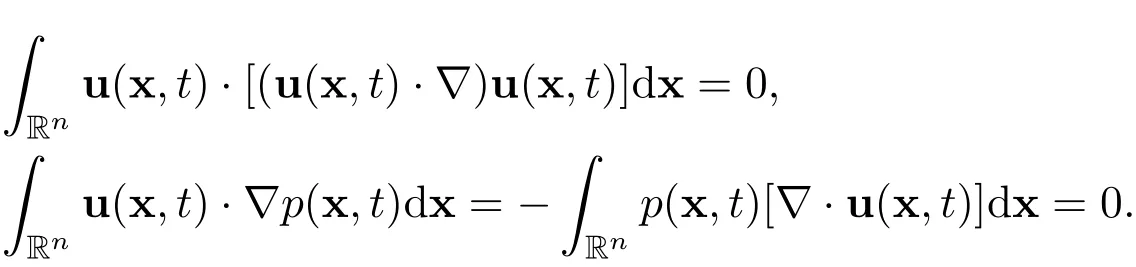
Applying the Parseval’s identity to the energy equation leads to
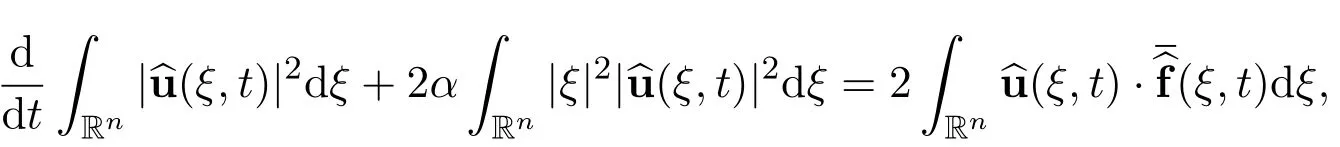
Multiplying this equation by(1+t)2n,we get

Applying Cauchy-Schwartz’s inequality to the last integral term,we get
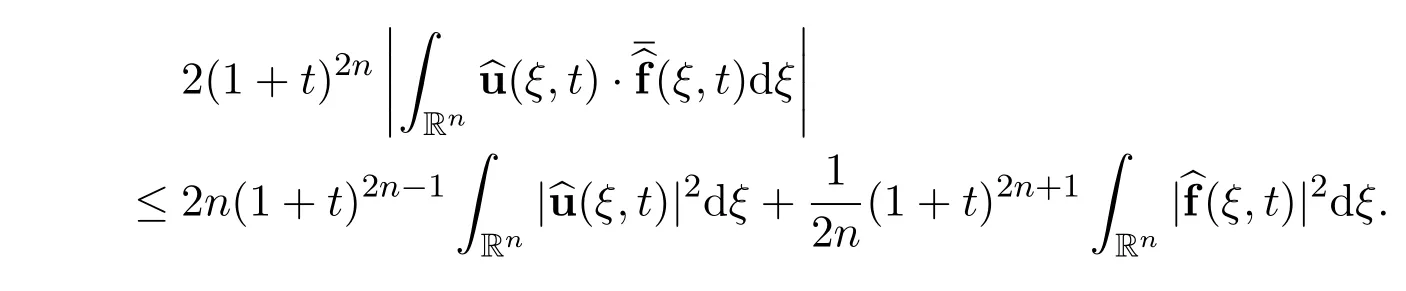
Now we have the differential inequality
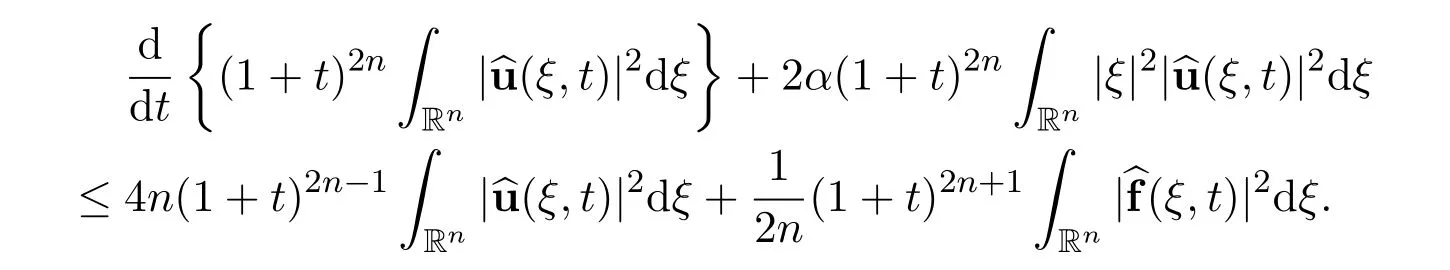
Step 2The splitting of the frequency space.Define
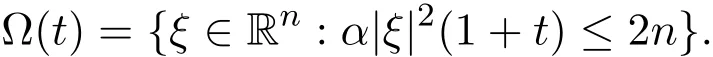
Then there hold the following estimates
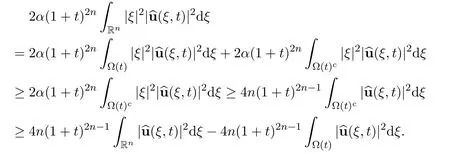
Now the above differential inequality becomes
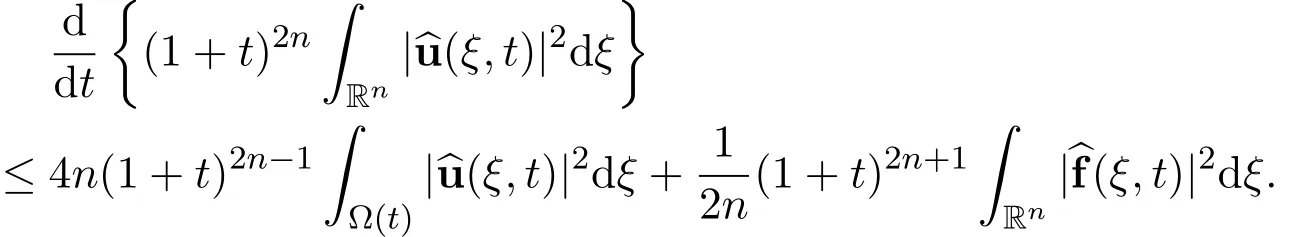
Step 3The elementary uniform energy estimate.There holds the following uniform energy estimate for the global weak solution
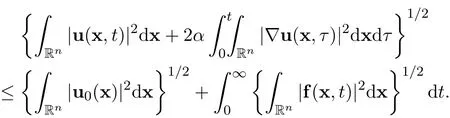
Step 4The representation of the Fourier transformation ub(ξ,t).There holds the following representation for the Fourier transformation
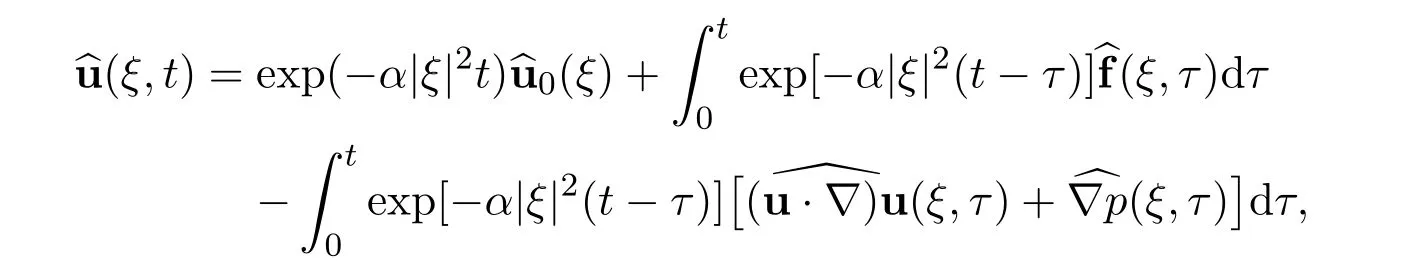
for all(ξ,t)∈ Rn×R+.
Step 5The elementary estimates ofand its integral

By definition of the Fourier transformation,we have

Then there hold the following estimates

Therefore,there holds the following estimate

for all(ξ,t)∈ Rn×R+.
Step 6The elementary estimates of the Fourier transformationand its integralTaking the divergence of the n-dimensional incompressible Navier-Stokes equations leads to
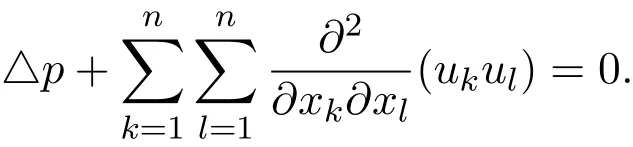
Performing the Fourier transform gives

There hold the following estimates and


for all ξ∈Rnand t>0.
Step 7The elementary estimate of the Fourier transformation ub(ξ,t).By using the representation of the Fourier transformation
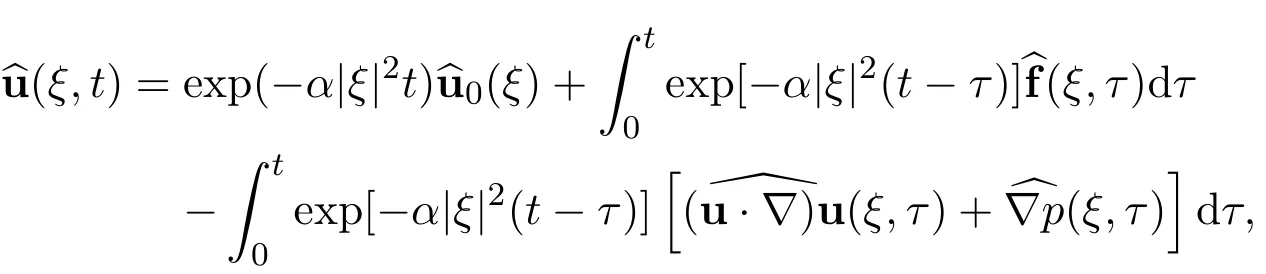
and the above estimates,we have the following estimates
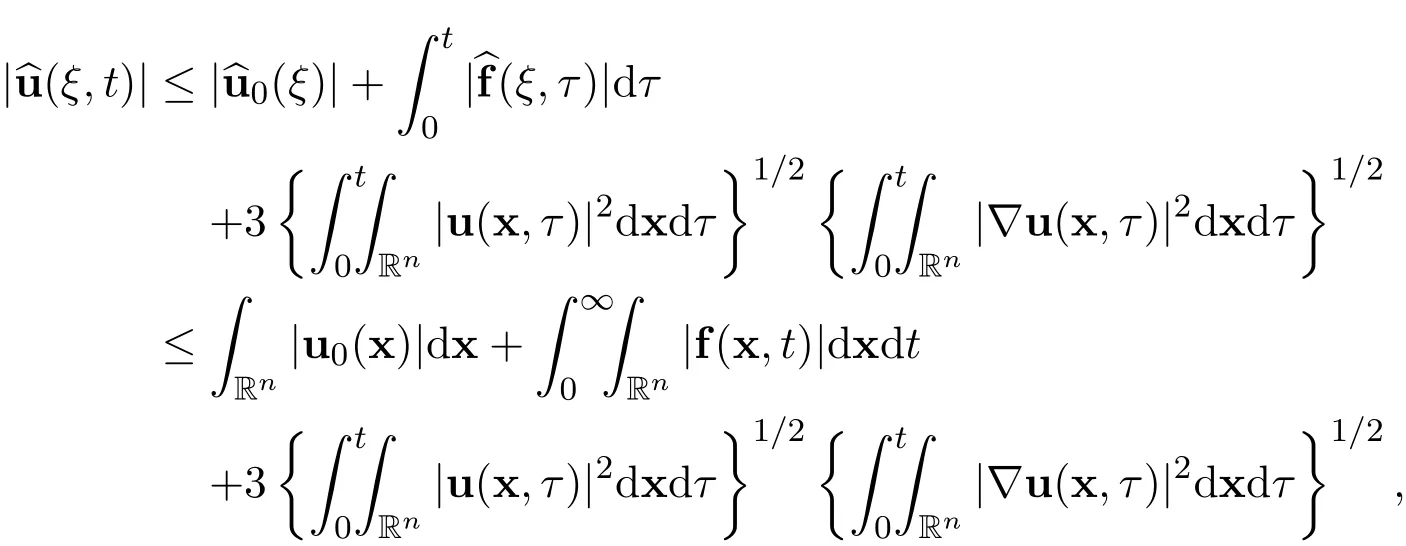
for all(ξ,t)∈ Rn×R+.
Step 8The estimate of the integralThere hold the following estimates
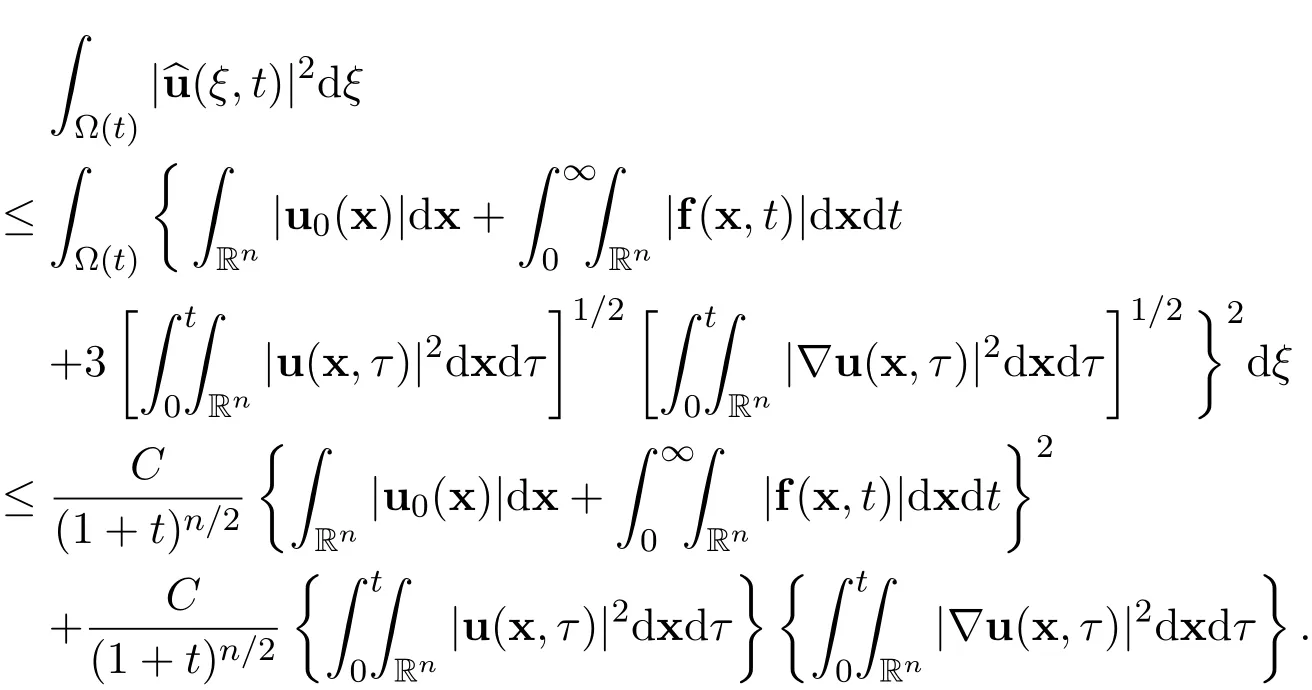
Step 9An energy inequality.By coupling together Steps 2 and 8,there hold the following estimates
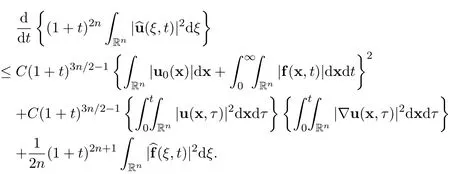
Integrating it with respect to time t gives
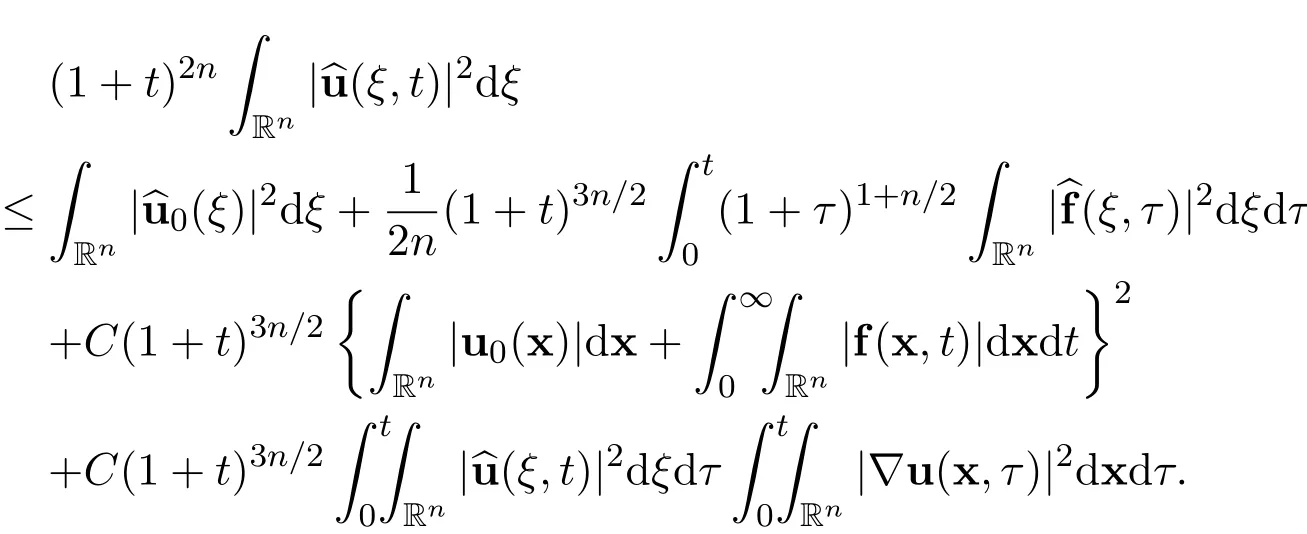
Step 10The application of a Gronwall’s inequality.Now there hold the following estimates
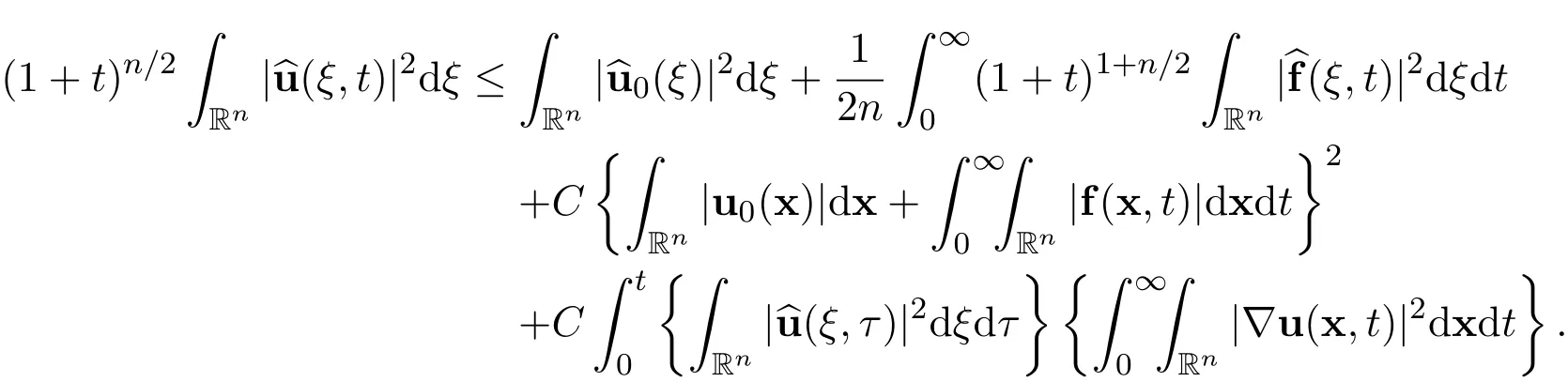
If we apply the Gronwall’s inequality,then we obtain the decay estimate for all n≥3 and for all time t>0.
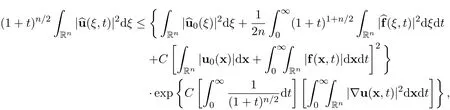
Step 11The elementary estimates of the Fourier transformations ub0(ξ),and.Suppose that there exist real scalar functions ϕkl∈ C1(Rn)∩L1(Rn)and ψkl∈ C1(Rn×R+)∩L1(Rn×R+),such that the initial function u0and the external force f satisfy
By using the definition of Fourier transform and Cauchy-Schwartz’s inequality,we have the following estimates
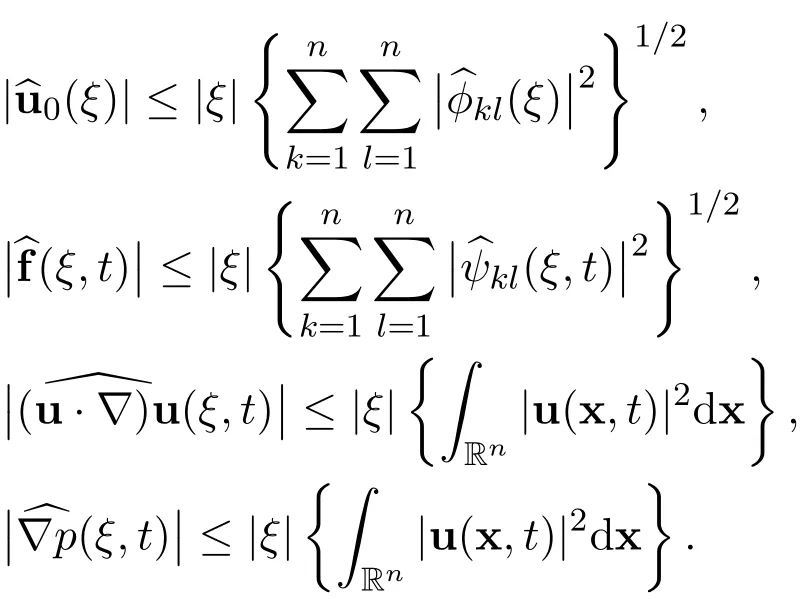
Step 12The decay estimate with sharp rate.By coupling together these estimates,Steps 4 and 11,we have the following estimates
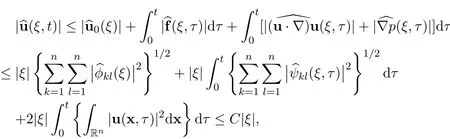
and
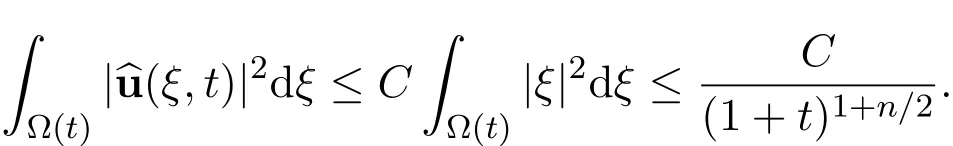
Now the above energy equation becomes
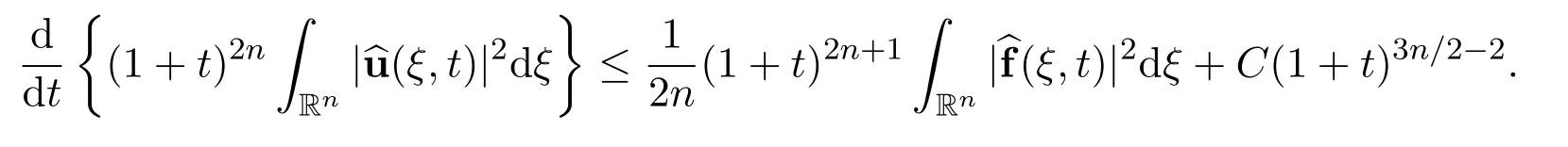
Integrating it with respect to time t gives
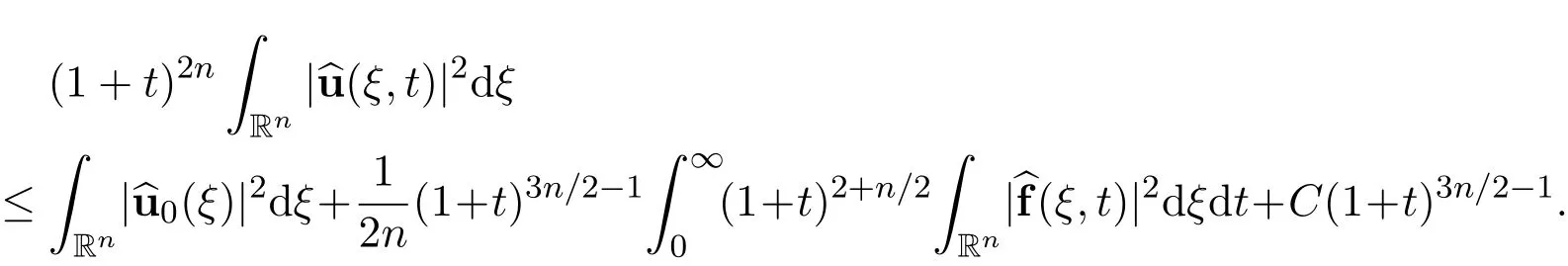
Therefore,we obtain the desired decay estimate with sharp rate
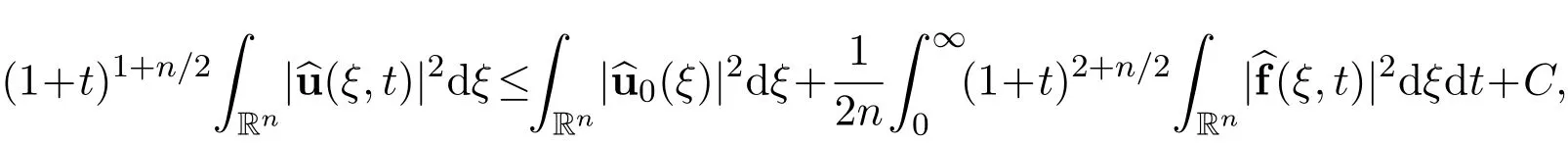
where C>0 is a positive constant,independent u and(x,t).The proof of Theorem 2 is completed.
3 Conclusions and Remarks
3.1Summary
Consider the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations

Suppose that the initial function u0∈ L1(Rn)∩L2(Rn)and the external force f∈L1(Rn×R+)∩L1(R+,L2(Rn)).Then there exists a global weak solution u∈L∞(R+,L2(Rn)),such that∇u∈L2(R+,L2(Rn)).Moreover,after a sufficiently long time,the global weak solution becomes small and smooth u∈L∞((T,∞),H2m+1(Rn)),such that∇u∈L2((T,∞),H2m+1(Rn)),where m≫1 is a sufficiently large positive integer and T≫1 is a sufficiently large positive constant,provided that the external force is also sufficiently small and smooth after a long time.Moreover,if the dimension n=2,if the initial function u0∈L1(R2)∩H2m+1(R2)and the external force f∈ L1(R2×R+)∩L1(R+,L2(R2))∩L2(R+,H2m(R2)),then there exists a global smooth solution u∈L∞(R+,H2m+1(R2)),such that∇u∈L2(R+,H2m+1(R2)),where m≥1 is a positive integer.Suppose that there exists the following integral
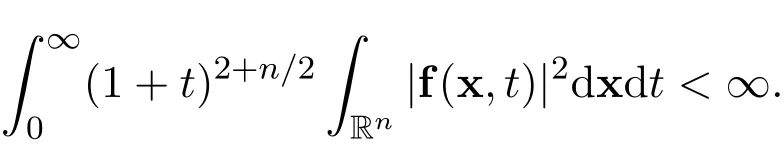
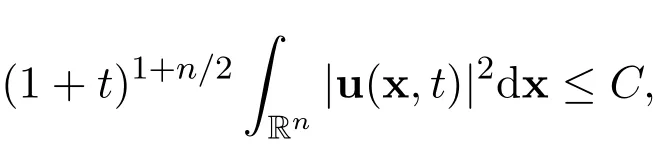
Then there holds the following decay estimate with sharp rate for all t>0,where C>0 is a positive constant,independent of u and(x,t).
The ideas and methods developed in this paper may be used to study the decay estimates with sharp rates of the global weak solutions of many other very interesting equations with dissipations.The rigorous mathematical analysis of the decay estimate with sharp rate of the global weak solution of the nonhomogeneous incompressible Navier-Stokes equations has never been established before,though the same results for the homogeneous Navier-Stokes equations has been established.
3.2 Remarks
Let the initial function u0∈L1(Rn)∩H2m+1(Rn)and the external force f∈L1(Rn×R+)∩L1(R+,L2(Rn))∩L2(R+,H2m+1(Rn)).Motivated by the existence and uniqueness of the local smooth solution u ∈ L∞((T,∞),H2m+1(Rn)),such that∇u∈ L2((T,∞),H2m+1(Rn)),without loss of generality,suppose that there exists a global smooth solution to the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations(1)-(2):u∈L∞(R+,H2m+1(Rn)),such that∇u∈L2(R+,H2m+1(Rn)),where m≥1 is a positive integer.
Suppose that there exist the following integrals
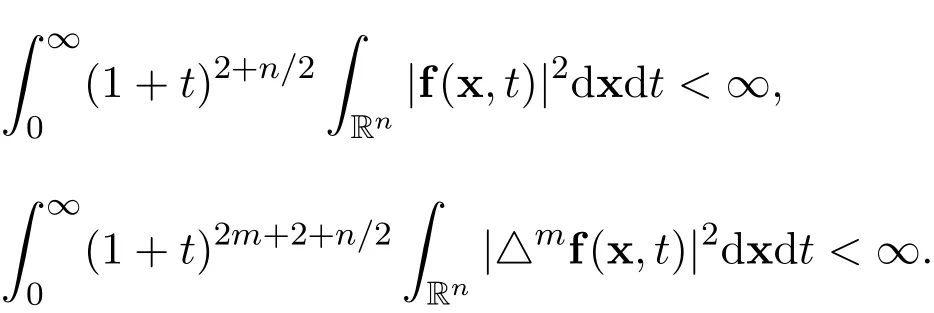
Suppose that there exist real scalar functions ϕkl∈ C1(Rn)∩ L1(Rn)and ψkl∈C1(Rn× R+)∩ L1(Rn× R+),for all k=1,2,···,n and l=1,2,···,n,such that
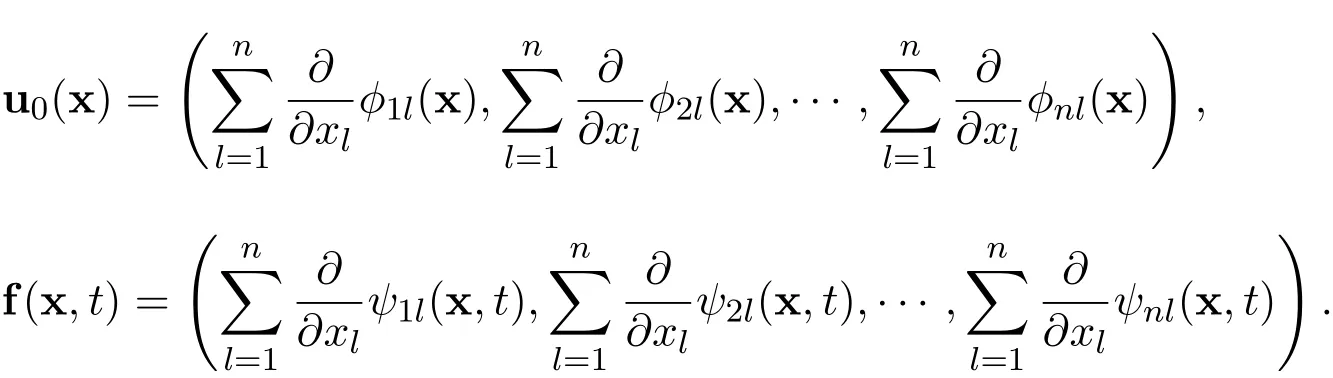
These assumptions are motivated by the structures of the nonlinear functions(u·∇)u and∇p,and by the following facts
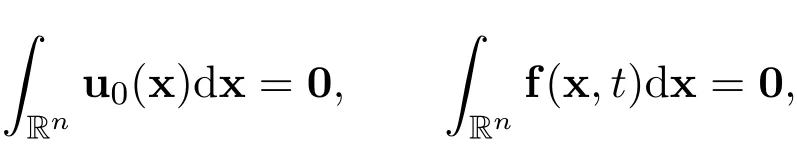
for all t>0.
Note that
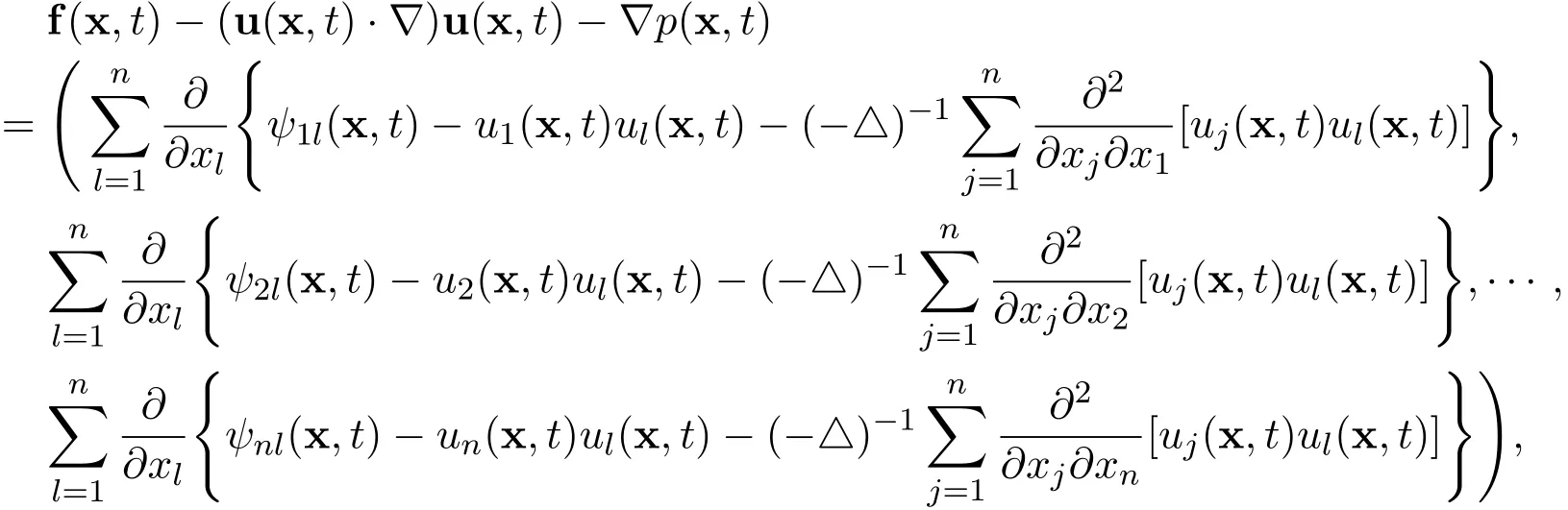
where
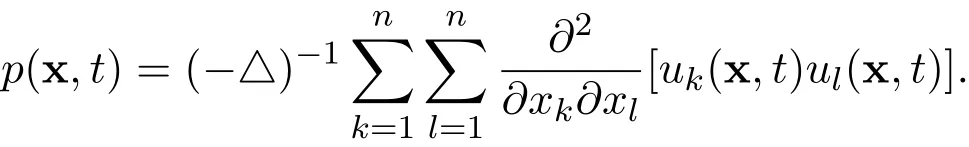
We will establish the following exact limits of the global smooth solution of the Cauchy problem for the n-dimensional incompressible Navier-Stokes equations
in terms of α,m,n,the integrals of the initial function and the external force

3.3 Some technical lemmas
Recall that the Fourier transformation and the inverse Fourier transformation of u∈L2(Rn)is defined by
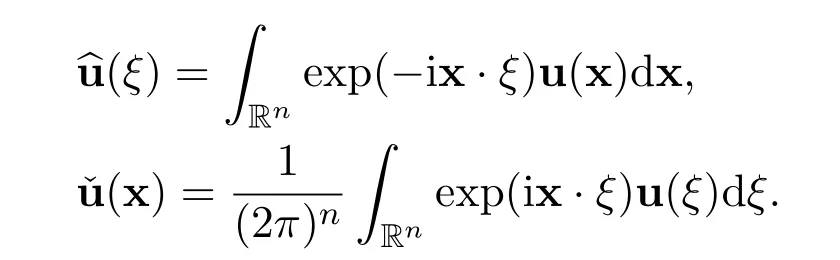
Lemma 1(Parseval’s identity)There holds the following identity
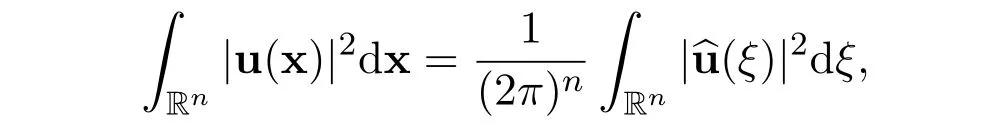
for all functionsu∈L2(Rn).
Lemma 2(The general Gronwall’s inequality)Let the nonnegative continuous functionsg≥0andh≥0satisfy the following inequality
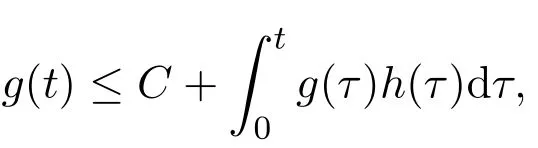
for allt>0,whereC>0is a positive constant,the functionh∈L1(0,∞).Then there holds the following estimate
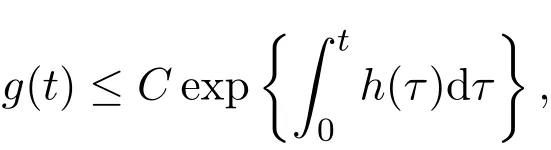
for allt>0.
杂志排行
Annals of Applied Mathematics的其它文章
- ON THE NORMALIZED LAPLACIAN SPECTRUM OF A NEW JOIN OF TWO GRAPHS∗
- ASYMPTOTIC NORMALITY OF THE NONPARAMETRIC KERNEL ESTIMATION OF THE CONDITIONAL HAZARD FUNCTION FOR LEFT-TRUNCATED AND DEPENDENT DATA∗†
- RAMSEY NUMBER OF HYPERGRAPH PATHS∗
- SOME NEW DISCRETE INEQUALITIES OF OPIAL WITH TWO SEQUENCES∗†
- STABILITY ANALYSIS OF A LOTKA-VOLTERRA COMMENSAL SYMBIOSIS MODEL INVOLVING ALLEE EFFECT∗†
- A LOTKA-VOLTERRA PREY-PREDATOR SYSTEM WITH FEEDBACK CONTROL EFFECT∗
