SOME NEW DISCRETE INEQUALITIES OF OPIAL WITH TWO SEQUENCES∗†

Xu Han,Sha Li,Qiaoluan Li

(College of Math.and Information Science,Hebei Normal University,Shijiazhuang 050024,Hebei,PR China)

Abstract In this paper,we establish some new discrete inequalities of Opial-type with two sequences by making use of some classical inequalities.These results contain as special cases improvements of results given in the literature,and these improvements are new even in the important discrete case.

Keywords Opial type inequality;Hölder’s inequality;forward difference operator;backward difference operator

1 Introduction

In 1960,Opial[1]established the following important integral inequality:

Theorem ALetf(x)∈C1[0,h]be such thatf(0)=f(h)=0,andf(x)>0in(0,h).Then

whereis the best possible.

Inequality(1.1)is known in the literature as Opial inequality.For the past few years,Opial’s inequality and its generalizations,extensions and discretizations have played a fundamental role in establishing the existence and uniqueness of initial and boundary value problems for ordinary and partial differential equations as well as difference equations.Many mathematicians gave the improvements and generalizations in last few decades to add the considerable contribution in the literature(see,for instance,[2-10]).

The paper is motivated by the work of K.C.Hsu and K.L.Tseng[11]and their discrete versions of Opial type inequalities about forward difference operator.We will prove some new discrete inequalities of Opial type with two sequences.In this paper,we denoteby a sequence of real numbers,the operators∆and∇by∆xi=xi+1−xiand ∇xi=xi−xi−1respectively.In the next section,we will give the improvements of discrete inequalities of Opial type.

2 Main Results

Throughout this section,let m,n>0 and c(m,n)=max{m,n}.We start with the following theorem.

Theorem 2.1Letandbe sequences of real numbers withx0=y0=0.Then,the following inequality holds

wheren≥1,m>0.

Proof Since x0=y0=0,we have the following identity

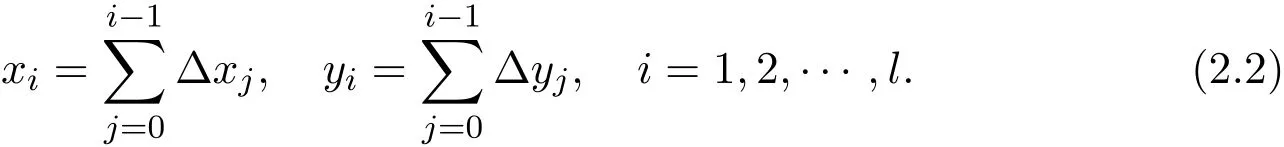
For n=1,by(2.2),the left of inequality(2.1)can be written as

For n>1,using the Hölder’s inequality with indices{,n},we have

From(2.3)and(2.4),for n≥1,we get that

Next,we need the following inequalities to complete our result:

where α,β >0.Then

Using inequalities(2.5)and(2.7),we drive inequality(2.1).This completes the proof.

Theorem 2.2Letandbe sequences of real numbers withx0=y0=0.Then,we have the following inequality

wheren≥1,m>0.

Proof Since x0=y0=0,we have the following identity

For n=1,by(2.9),the left of inequality(2.8)can be written as

For n>1,using the Hölder’s inequality with indices{,n},we have

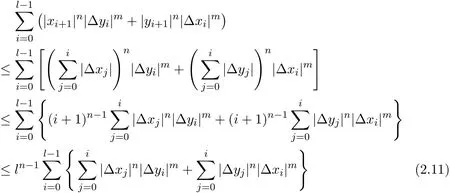
From(2.10)and(2.11),for n≥1,we get that

By(2.6),we have

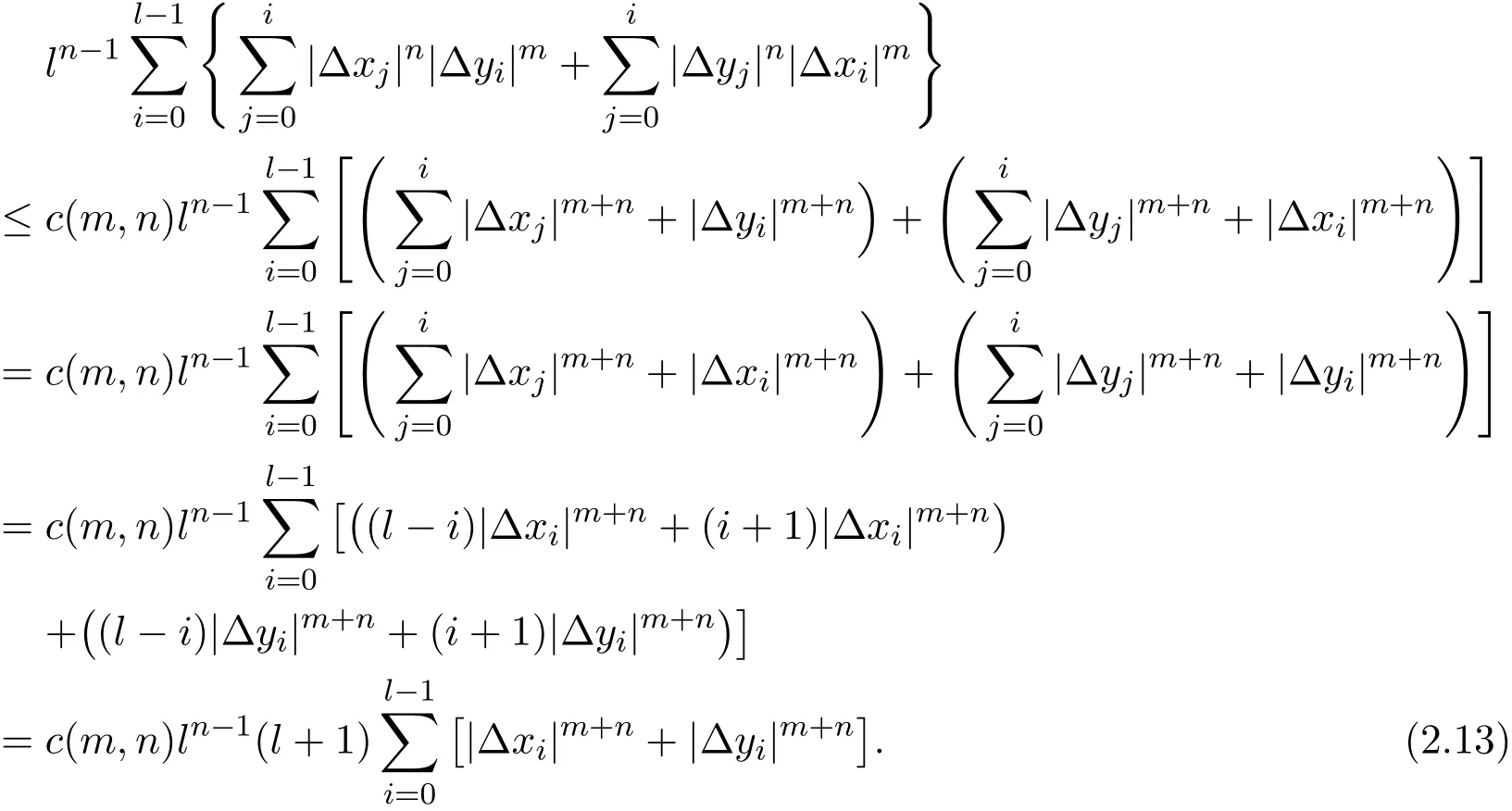
Using inequalities(2.12)and(2.13),we drive inequality(2.8).This completes the proof.

Corollary 2.1Letandbe sequences of real numbers withx0=y0=0.Then,we have the following inequality

wheren≥1,m>0.

Proof Since

it follows from inequality(2.8)that

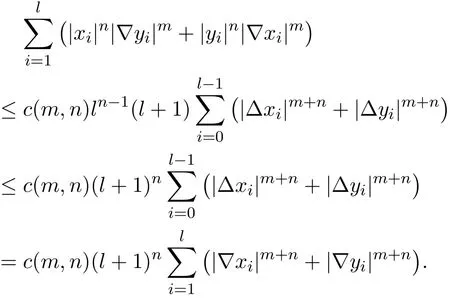
This completes the proof.

Theorem 2.3Letandbe sequences of real numbers withxN=yN=0.Then,we have the following inequality

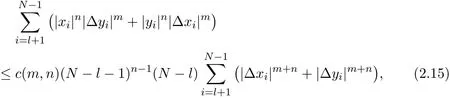
wheren≥1,m>0.

Proof Let xi=XN−i,yi=YN−i,where i=l+1,i+2,···,N.Then

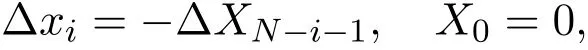
and

where i=l+1,i+2,···,N − 1.Using(2.8),we can obtain

This completes the proof.

Theorem 2.4Letandbe sequences of real numbers withx0=xN=0,y0=yN=0.Then,we have the following inequality

wheren ≥ 1,m>0,and[·]is the greatest integer function.

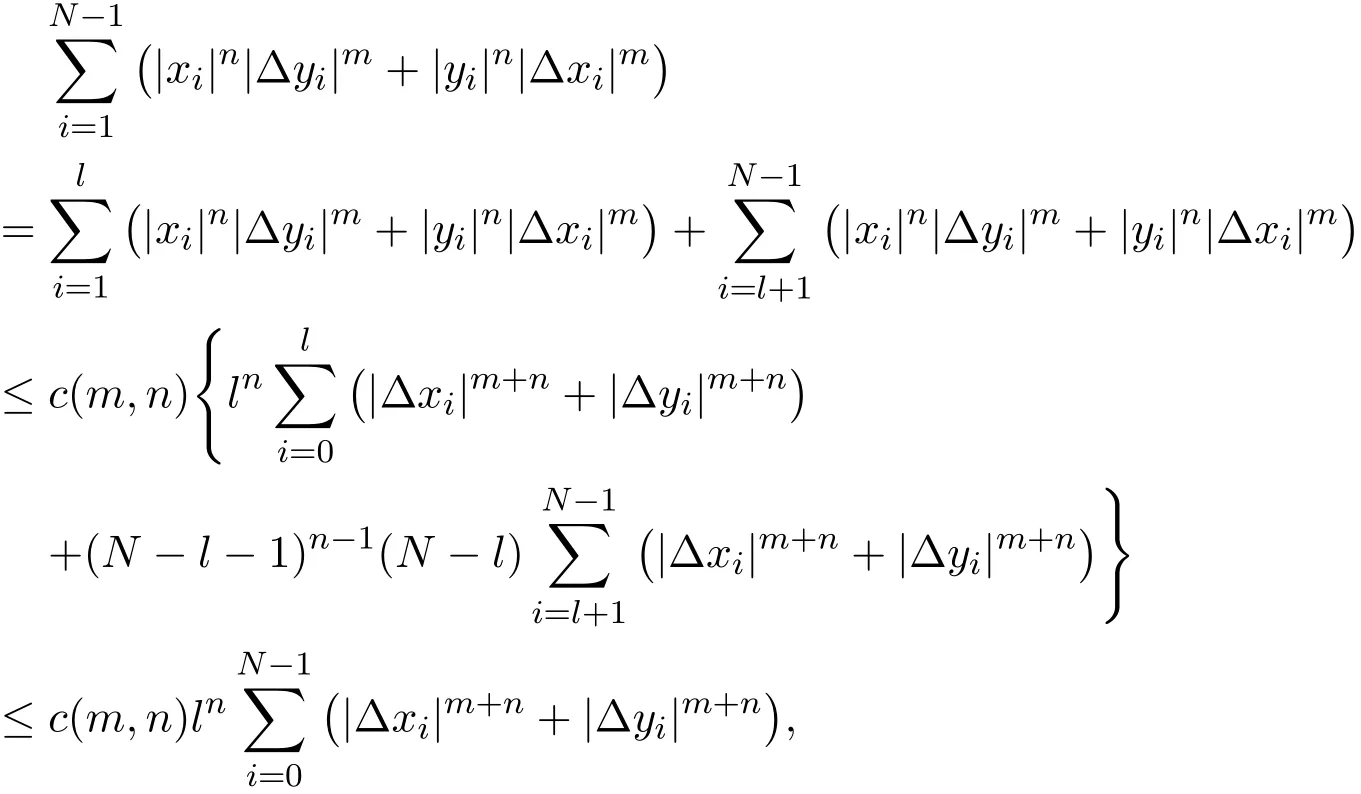
thus inequality(2.16)holds.This completes the proof.