STABILITY ANALYSIS OF A LOTKA-VOLTERRA COMMENSAL SYMBIOSIS MODEL INVOLVING ALLEE EFFECT∗†
2019-01-09XinyuGuan
Xinyu Guan
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
Abstract In this paper,we present a stability analysis of a Lotka-Volterra commensal symbiosis model subject to Allee effect on the unaffected population which occurs at low population density.By analyzing the Jacobian matrix about the positive equilibrium,we show that the positive equilibrium is locally asymptotically stable.By applying the differential inequality theory,we show that the system is permanent,consequently,the boundary equilibria of the system is unstable.Finally,by using the Dulac criterion,we show that the positive equilibrium is globally stable.Although Allee effect has no in fluence on the final densities of the predator and prey species,numeric simulations show that the system subject to an Allee effect takes much longer time to reach its stable steady-state solution,in this sense that Allee effect has unstable effect on the system,however,such an effect is controllable.Such an finding is greatly different to that of the predator-prey model.
Keywords Lotka-Volterra commensal symbiosis model;Allee effect;global stability
1 Introduction
Commensalism is one of the basic interrelationships between the species,where a species in flicts advantage to the other species without any harm or benefits received by the other.Epiphyte and plants with epiphyte,squirrel and the oak,etc,are the common typical commensal relationship,for more background about commensalism,one could see[1-5]and the references cited therein.
Recently,Sun and Wei[6]proposed the following two species commensalism model:

where r1,r2,k1,k2and a are all positive constants.The system admits four equilibria:
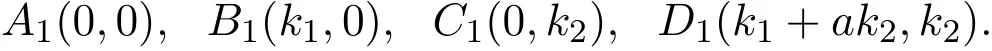
By linearizing the system at equilibrium,the authors investigated the stability of the above equilibrium points,and obtained the following results.
Theorem A
(1)A1(0,0))is a unstable node;
(2)B1(k1,0)is a saddle point;
(3)C1(0,k2)is a saddle point;
(4)D1(k1+ak2,k2)is a stable node.
But we notice that the author did not give any information about the global stability property of the equilibrium.Based on(1.1),the scholars in[1-5,7-13]proposed varies commensalism models,and many interesting results were obtained,which have greatly enriched and improved the commensalism models during the last decade.For example:The dynamic behaviors of an impulsive periodic Lotka-Volterra commensal symbiosis model was studied in[1];a two species commensal symbiosis model with Holling type functional response was investigated in[2];a nonautonomous discrete two-species Lotka-Volterra commensalism system with delays was considered in[4];sufficient conditions were obtained for the existence of positive periodic solution of a discrete commensal symbiosis model with Holling II functional response in[10];a two-species commensal symbiosis model with ratiodependent functional response was proposed in[11],etc.However,to this day,to the best of the authors knowledge,still no scholars consider the in fluence of Allee effect on the commensalism model.
Defined as a reduce per-capita population growth rate at low densities,Allee effect can be caused by difficulties in finding a mate or predator avoid danger or defense[14,15].It is well known that Allee effect has important consequences for population dynamics.In recent years,there are many papers concerned with Allee effect of the predator-prey system and competition system,etc,see[16-22]and the references cited therein.Their studies demonstrated that Allee effect can have important consequences on local stability property of the equilibrium,the equilibrium solution may be changed from stable to unstable or vice versa.However,the papers[16-22]did not investigate the global stability property of the positive equilibrium of the system.Also,to this day,still no scholars study the in fluence of Allee effect on the commensalism model.Stimulated by the works of[16,20],in this paper,we propose the following commensalism model with Allee effect:

Our interesting issues is:
1.Find out the in fluence of the parameter u,which reflects the strength of Allee effect;
2.Investigate the global dynamic behaviors of the system,specially,to give an positive answer to the global stability property of the positive equilibrium of systems(1.1)and(1.2).
We will present both local stability analysis of system(1.2),and investigate the global stability property of equilibrium solutions of models(1.1)and(1.2).The stability conditions are compared through analysis supported by numerical simulations.
We arrange the paper as follows:In the next section,we investigate the existence,persistent and local stability property of the equilibria of system(1.2).In Section 3,Dulac criterion are applied to investigate the global stability property of positive equilibrium of system(1.2).In Section 4,some examples together with their numeric simulations are presented to show the feasibility of our main results.We end this paper by a brief discussion.
2 Local Stability and Persistence of the System
We now analyse the stability of steady-state solutions of system(1.2),subject to an Allee effect on the second population.Defining

the steady-state solutions of(1.2)are obtained by solving the equations f(x,y)=0 and g(x,y)=0.Obviously,
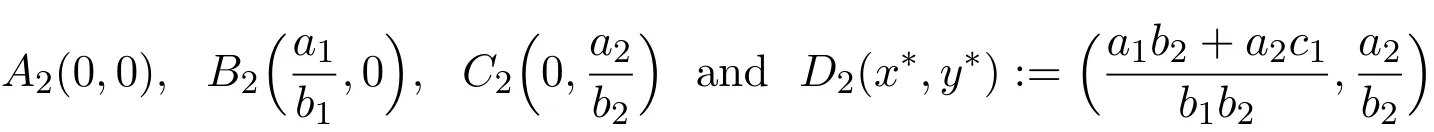
are four equilibria of system(1.2).By comparing with the equilibria of system(1.1),we can easily conclude that the values of four equilibria of system(1.2)have no change.From Theorem A,only the positive equilibrium point is locally asymptotically stable in system(1.1).Hence,from a biological point of view,we are mainly interested in the positive equilibrium solution of system(1.2).
Lemma 2.1[23]Consider the following equation

where the functionF(N)satisfies the following conditions:
(1)There is anN∗,such thatF(N∗)=0;
(2)for allN∗>N>0,F(N)>0;
(3)for allN>N∗>0,F(N)<0.ThenN∗is globally stable.
Lemma 2.2Consider the following equation
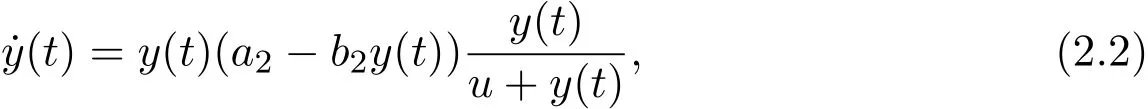
then the unique positive equilibriumy∗=is globally stable.
Proof Set
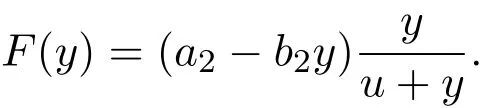
Then
(1)There is a y∗=,such that F(y∗)=0;
(2)for all y∗>y>0,F(y)>0;
(3)for all y>y∗>0,F(y)<0.
Therefore,all the conditions of Lemma 2.1 are satisfied,and it follows from Lemma 2.1 that y∗is globally stable.This ends the proof of Lemma 2.2.
Lemma 2.3The second species of system(1.2)is permanent.
Proof It follows from the second equation of system(1.2)and Lemma 2.2 that y∗=is globally stable,that is,

For ε>0 enough small,there exists a T>0,when t>T,we have

Hence y(t)is finally bounded above and below,and the second species of system(1.2)is permanent.This ends the proof of Lemma 2.3.
As a direct corollary of Lemma 2.2 of Chen[24],we have:
Lemma 2.4Ifa>0,b>0and≥x(b−ax),whent≥0andx(0)>0,we have
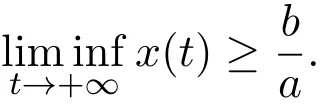
Ifa>0,b>0and≤x(b−ax),whent≥0andx(0)>0,we have
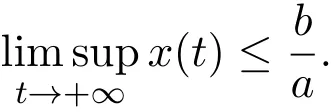
Theorem 2.1System(1.2)is permanent.
Proof In Lemma 2.3,we have proved that the second species of system(1.2)is permanent,now we will prove the permanence of the first species.Let x(t)be the positive solution of the first species of system(1.2).
From the first equation of system(1.2)and the right part of inequalities(2.4),when t≥T,we obtain
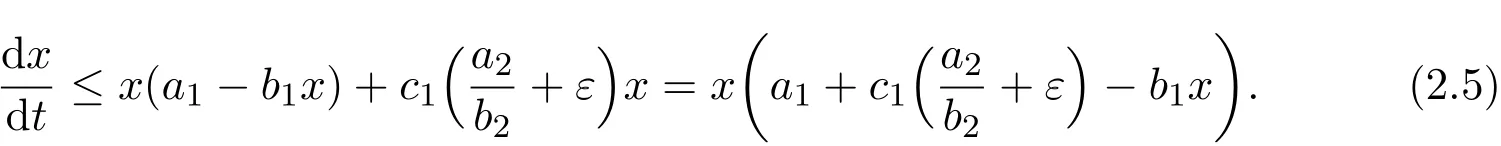
Thus,as a direct corollary of Lemma 2.3,we have

When t≥0,from the first equation of system(1.2),we also have

Applying Lemma 2.3 to(2.7),we have

(2.6)and(2.8)show that the first species of system(1.2)is permanent.
This ends the proof of Theorem 2.1.
Theorem 2.2 D2(x∗;y∗)is locally asymptotically stable,andA2(0,0),B2(,0)andC2(0,)are locally unstable.
Proof The Jacobian matrix of model(1.2)at an equilibrium E(x,y)is
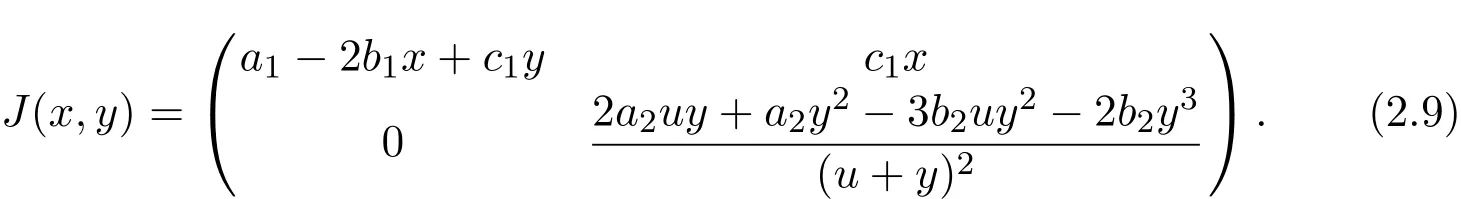
Now we have four cases to discuss the stability of equilibria of model(1.2).
Case 1For A2(0,0),we have

Obviously,the two eigenvalues of J(A2)are λ1=a1>0 and λ2=0.Hence,the equilibrium A2is non-hyperbolic.
Case 2For B2(,0),we have

Obviously,the two eigenvalues of J(B2)are λ1= −a1<0 and λ2=0.And so,the equilibrium B2is also non-hyperbolic.
Case 3For C2(0,),we have

The characteristic equation of the variational matrix is
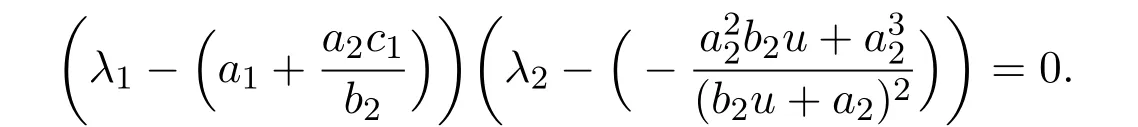
Obviously,the two eigenvalues of J(C2)are

then C2(0,2)is a saddle point.
Case 4For D2(x∗;y∗),
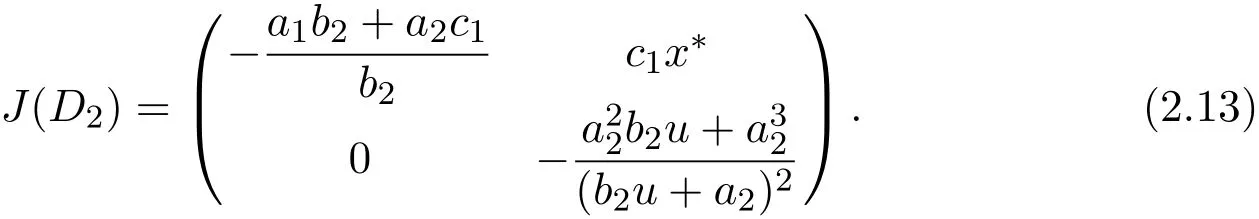
The characteristic equation of the variational matrix is
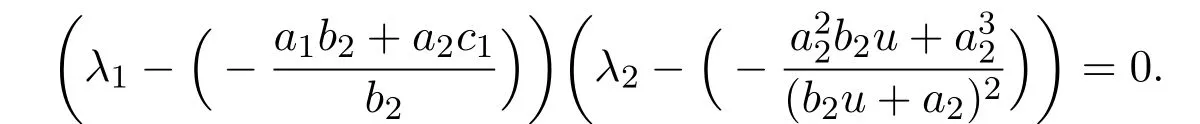
Obviously,the two eigenvalues of J(x∗,y∗)are
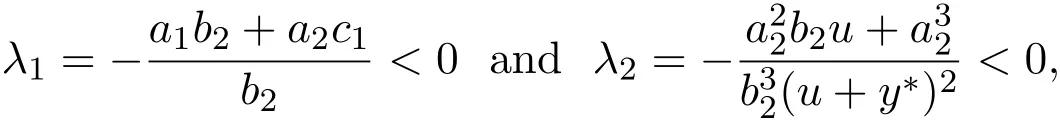
then D2(x∗,y∗)is a stable node.
For Cases 1 and 2,both A2and B2are non-hyperbolic,and we could not judge the stability property of these two equilibria by using the variational matrix.However,from Theorem 2.1,we know that system(1.2)is permanent,which indicates that no solution could approach to A2(0,0)and B2(,0),which means that A2(0,0)and B2(,0)are locally unstable.This ends the proof of Theorem 2.2.
3 Global Stability
In this part,we first give the following theorem,which is concerned with the global stability property of system(1.1).
Theorem 3.1The positive equilibriumD1(k1+ak2,k2)of system(1.1)is globally asymptotically stable.
Proof For convenience,making the following transformations:and,we can rewrite model(1.1)as follows:
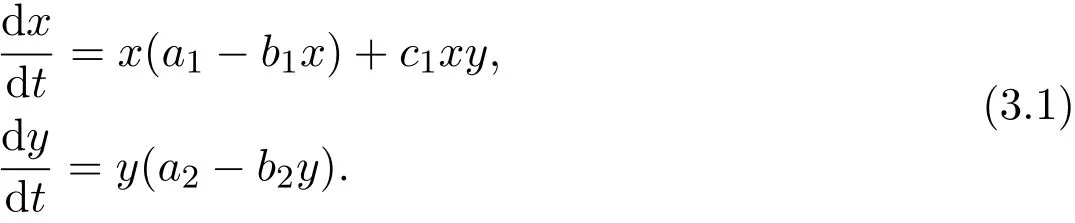
Set
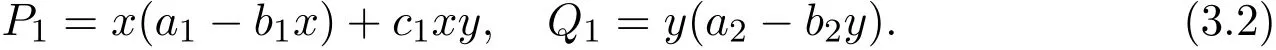
From Theorem A,system(1.1)admits a unique locally stable positive equilibrium D1(k1+ak2,k2).Now consider the Dulac function u1(x,y)=x−1y−1,then by simple computation,we have
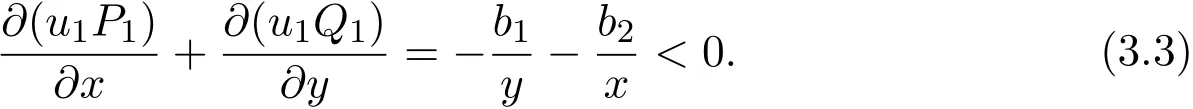
By Bendixson-Dulac theorem[25],there is no closed orbit in area.So D1(k1+ak2,k2)is globally asymptotically stable.This completes the proof of Theorem 3.1.
Theorem 3.2The positive equilibriumD2(x∗,y∗)of system(1.2)is globally asymptotically stable.
Proof We have showed that the positive equilibrium is locally stable.Now we further investigate the global stability property of the positive equilibrium.
Set
From Theorem 2.2,system(1.2)admits a unique locally stable positive equilibrium D2(x∗,y∗).Now consider the Dulac function u2(x,y)=x−1y−2,then

By Bendixson-Dulac theorem[25],there is no closed orbit in area R+2.So D2(x∗,y∗)is globally asymptotically stable.This completes the proof of Theorem 3.2.
4 Numeric Simulations
In this section,we shall report on numerical simulations of the commensal symbiosis model with or without Allee effect,defined by(1.2)and(3.1),respectively.In each simulations below,parameters are set as a1=3,b1=6,c1=2,a2=2 and b2=4,hence we can simply calculate that the steady-state solutions of systems(1.2)and(3.1)are D1=D2=(x∗,y∗) ∼=(0.6667,0.5).We verify our conclusions by changing the initial values of x(0)and y(0)and Allee constant u.
In Figures 1 and 2,we compare the time evolutions of the species densities with and without Allee effect.Both graphs show that the trajectories of the system subject to Allee effect approach the equilibrium solution more slowly than that of the model without Allee effect.As a supplement to Figures 1 and 2,Figures 3-5 illustrate that Allee effect does not change the population densities of both species at the stable steady-state solutions.
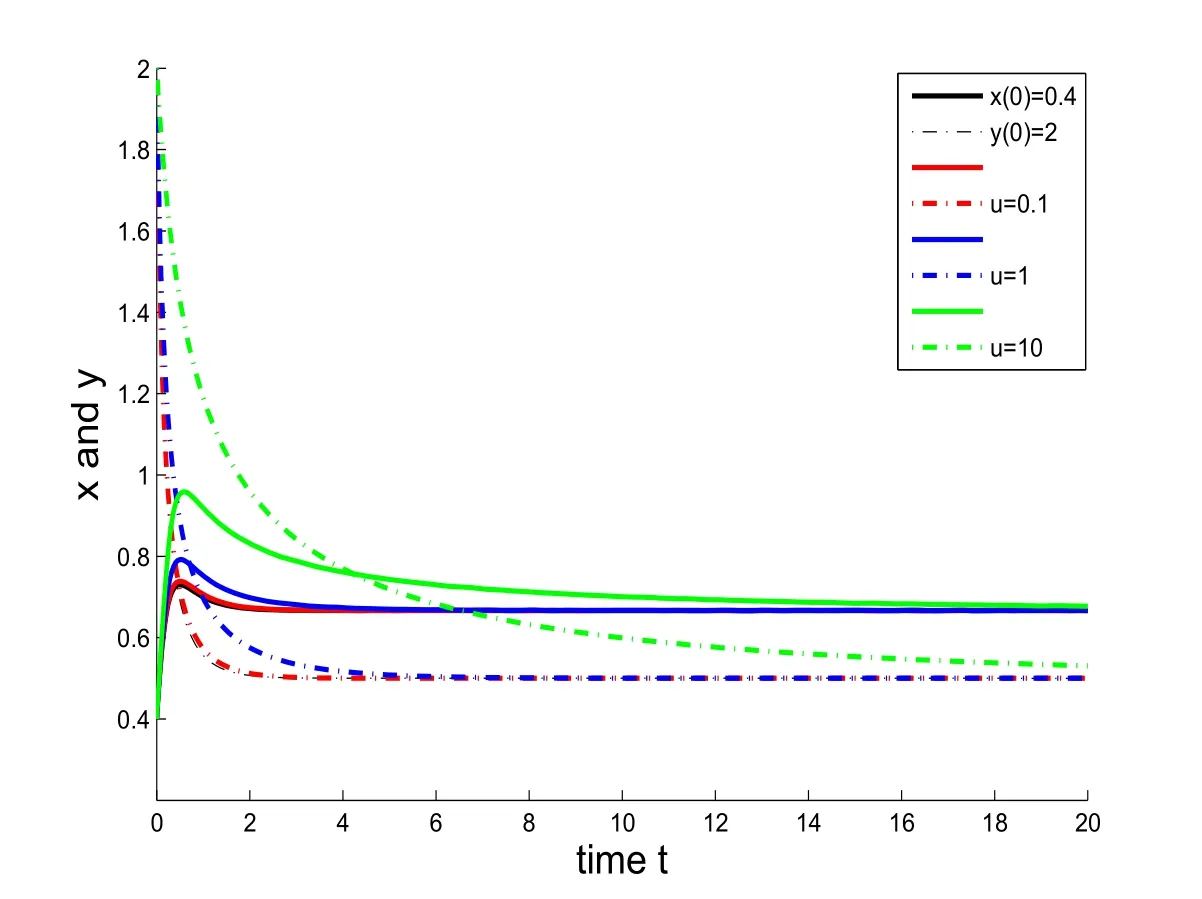
Figure 1:(a)Time-population density graphs denoted by x(t)(solid line)and y(t)(dashed line).(b)The initial conditions are x(0)=0.4 and y(0)=2,and parameters are a1=3,b1=6,c1=2,a2=2 and b2=4.(c)The Allee constant u has changed from u=0,0.1,1,10.As u=0 means the system without Allee effect.
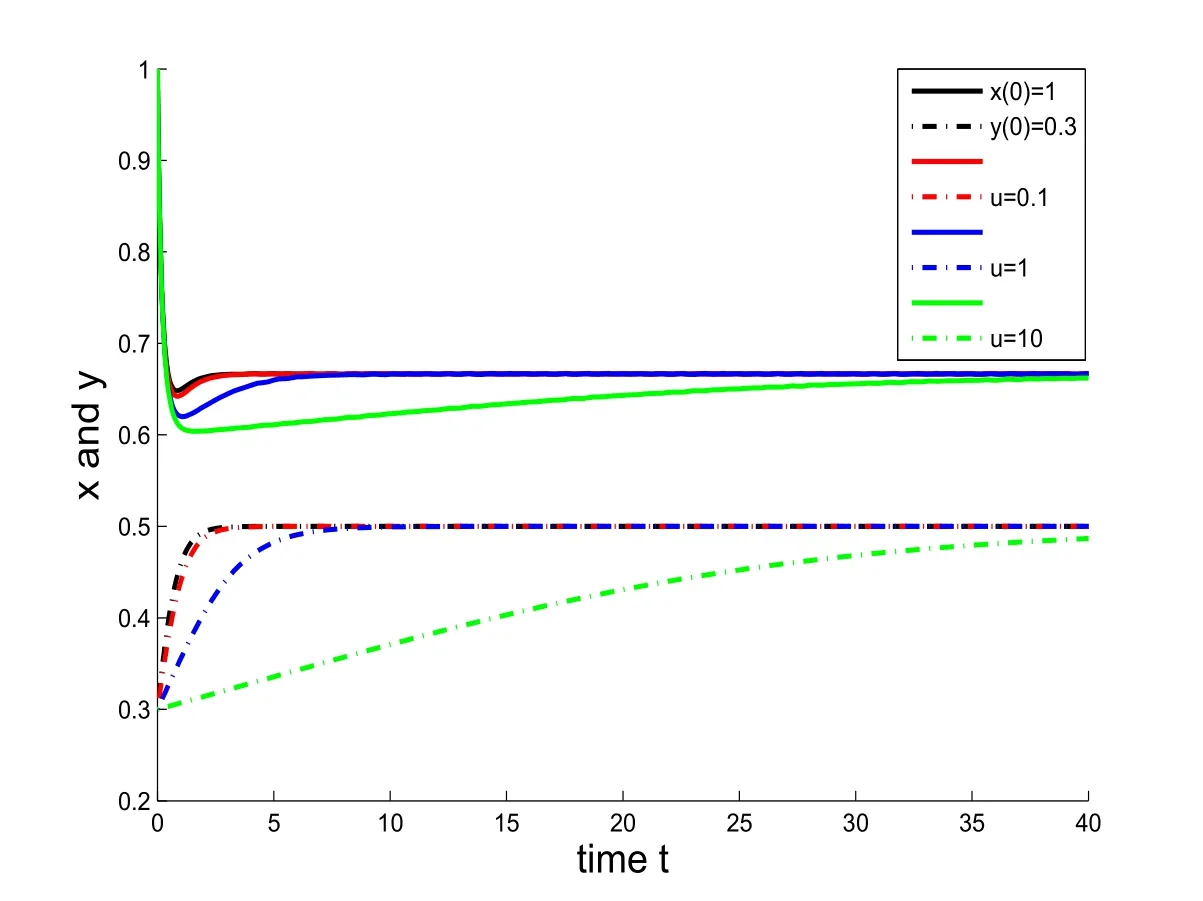
Figure 2:(a)Time-population density graphs denoted by x(t)(solid line)and y(t)(dashed line).(b)The initial conditions are x(0)=1 and y(0)=0.3,and parameters are a1=3,b1=6,c1=2,a2=2 and b2=4.(c)The Allee constant u has changed from u=0,0.1,1,10.As u=0 means the system without Allee effect.
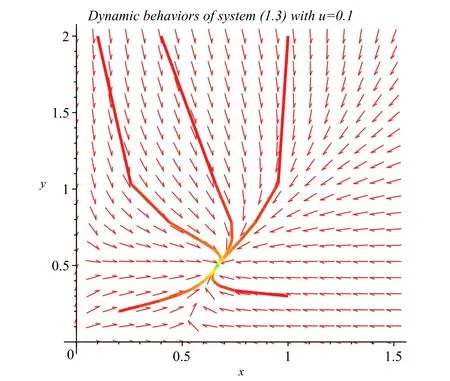
Figure 3:Numeric simulations of system(1.2)with a1=3,b1=6,c1=2,a2=2,b2=4 and the Allee constant u=0.1 and the initial condition(x(0),y(0))=(0.4,2),(1,0.3),(0.2,0.2),(1,2)and(0.1,0.2),respectively.

Figure 4:Numeric simulations of system(1.2)with a1=3,b1=6,c1=2,a2=2,b2=4 and the Allee constant u=1 and the initial condition(x(0),y(0))=(0.4,2),(1,0.3),(0.2,0.2),(1,2)and(0.1,0.2),respectively.
5 Disscussion
As Huseyin Merdan[20]pointed out,Allee effect may have a stabilizing or a destabilizing effect on population dynamics.However,both[16]and[20]focused the local stability property of the equilibrium.In this paper,we propose a twospecies commensal symbiosis model with Allee effect on the second population.Our study shows that the system always admits a unique positive equilibrium,which is globally stable.Also,since the express x∗and y∗is independent of u,Allee effect has no in fluence on the final density of the species.Such an finding is greatly different from that of predator-prey system,indeed,Huseyin Merdan[20]showed that if Allee effect is large enough,the predator-prey system considered could not have positive equilibrium,which means that the part of the species will be driven to extinction.Numerical simulations show that when one introduces Allee effect to the system,the system takes a longer time to reach its stable steady-state,it is in this sense,Allee effect has unstable effect on the system.
杂志排行
Annals of Applied Mathematics的其它文章
- NEW PROOFS OF THE DECAY ESTIMATE WITH SHARP RATE OF THE GLOBAL WEAK SOLUTION OF THE n-DIMENSIONAL INCOMPRESSIBLE NAVIER-STOKES EQUATIONS∗
- ON THE NORMALIZED LAPLACIAN SPECTRUM OF A NEW JOIN OF TWO GRAPHS∗
- ASYMPTOTIC NORMALITY OF THE NONPARAMETRIC KERNEL ESTIMATION OF THE CONDITIONAL HAZARD FUNCTION FOR LEFT-TRUNCATED AND DEPENDENT DATA∗†
- RAMSEY NUMBER OF HYPERGRAPH PATHS∗
- SOME NEW DISCRETE INEQUALITIES OF OPIAL WITH TWO SEQUENCES∗†
- A LOTKA-VOLTERRA PREY-PREDATOR SYSTEM WITH FEEDBACK CONTROL EFFECT∗
