A LOTKA-VOLTERRA PREY-PREDATOR SYSTEM WITH FEEDBACK CONTROL EFFECT∗
2019-01-09XiaofengChen
Xiaofeng Chen
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
Abstract In this paper,we propose a Lotka-Volterra prey-predator system with discrete delays and feedback control.Firstly,we show that solution of the system is bounded.Secondly,we obtain sufficient condition for the global stability of the unique positive equilibrium to the system.
Keywords Lotka-Volterra prey-predator system;feedback control;global stability
1 Introduction
During the last decades,many scholars have investigated the dynamic behaviors of systems with feedback control(see[1-10]).Gopalsamy and Weng[1] first introduced a feedback control variable into a competitive system:
They investigated the stability property of the positive equilibrium.Li and He[2]investigated the following single-species food-limited system with feedback control and delay

Shi,Chen and Wang[3]discussed a Lotka-Volterra prey-predator system with feedback control

They showed that a suitable feedback control on predator species can make the dynamic of prey species changes from extinction to global stability.
Note that all the above papers assumed that the feedback control item u(t)is in fluenced by the population level of the matured species.It is naturally to ask:What would happen if the feedback control item u(t)is in fluenced by the population level of the immature species.
Motivated by the above works,in this paper,we consider:

where u(t)is the indirect control variable,ri>0,τi>0,aij>0,i,j=1,2,c>0,e>0,d>0,τ=max{τ1,τ2},subject to
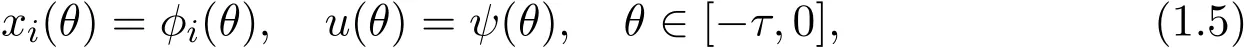
ϕi(θ)and ψ(θ)are nonnegative and bounded continuous functions on[−τ,0].
The organization of the paper is as follows.In the next section,we investigate the existence of positive equilibrium and the boundness property of the system;In Section 3,by constructing a Lyapunov functional,we show the global stability of the equilibriums under some assumptions.
2 Preliminaries
System(1.4)always admits a boundary equilibrium O(0,0,0).
Suppose that assumption r1a22−a12r2>0 holds.It is not difficult to verify that system(1.4)has a unique positive equilibrium(,,u∗):

Lemma 2.1Let(x1(t),x2(t),u(t))Tbe a solution of system(1.4)with the initial condition(1.5),Then(x1(t),x2(t),u(t))is positive and bounded for allt>0.
Proof Obviously,solutions(x1(t),x2(t),u(t))Tof system(1.4)with the initial condition(1.5)are positive for all t>0.By the first equation of system(1.4),we have

By a standard comparison principle and basic ODE theory it follows that
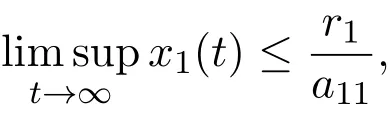
Hence,for any t>0,there exists a T1>0 such that
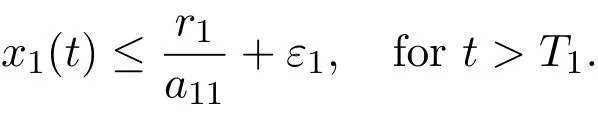
By the second equation of system(1.4),we have

This implies that
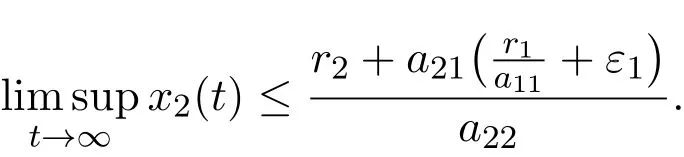
Setting ε1→ 0,it follows that

Therefore,for any ε2>0 small enough,there exists a T2>T1+ τ2>0,such that
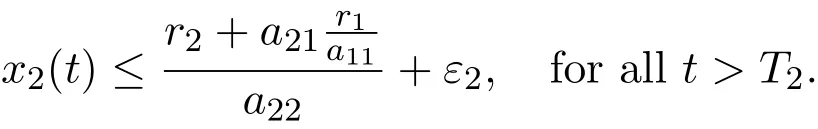
By the third equation of system(1.4),

which means that
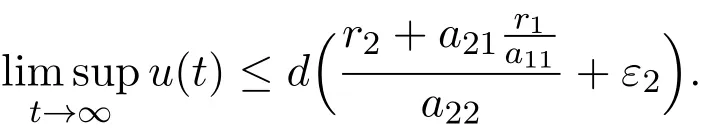
Letting ε2→ 0,it follows that
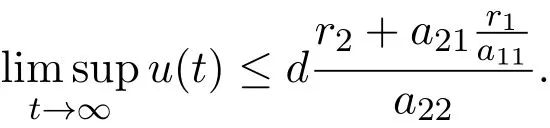
Therefore,for any ε3>0 small enough,there exists a T3>T2+ τ1>0,such that
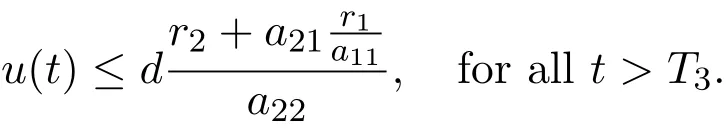
This completes the proof.
3 Main Result
Now,we give our main result.
Theorem 3.1Let(x1(t),x2(t),u(t))Tbe a solution of system(1.4)with the initial condition(1.5),Ifa11a22−a12a21>0,then the unique positive equilibrium of system(1.4)is globally asymptotically stable.
Proof Define a Lyapunov function as follows:
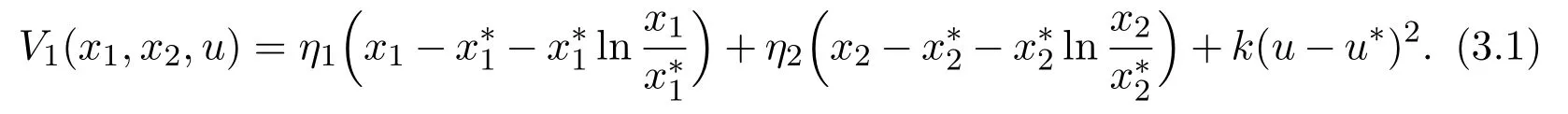
Note that system(1.4)can be rewritten as
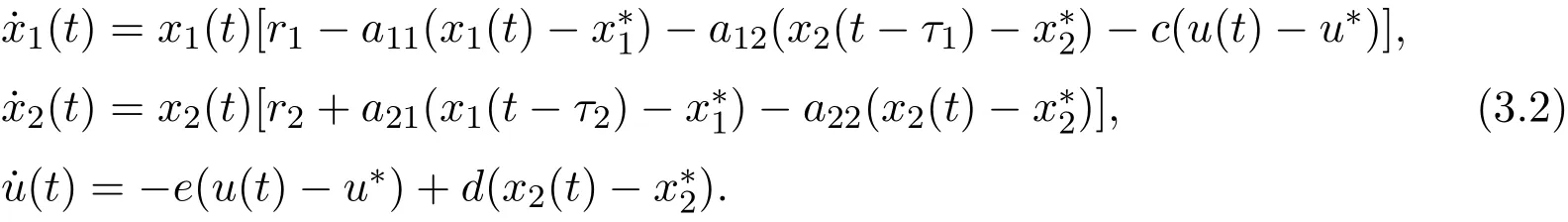
One could easily see that the function V1is zero at the equilibrium(,,u∗)and is positive for all other positive values of x1,x2and u.The time derivative of V1along the trajectories of(3.1)is
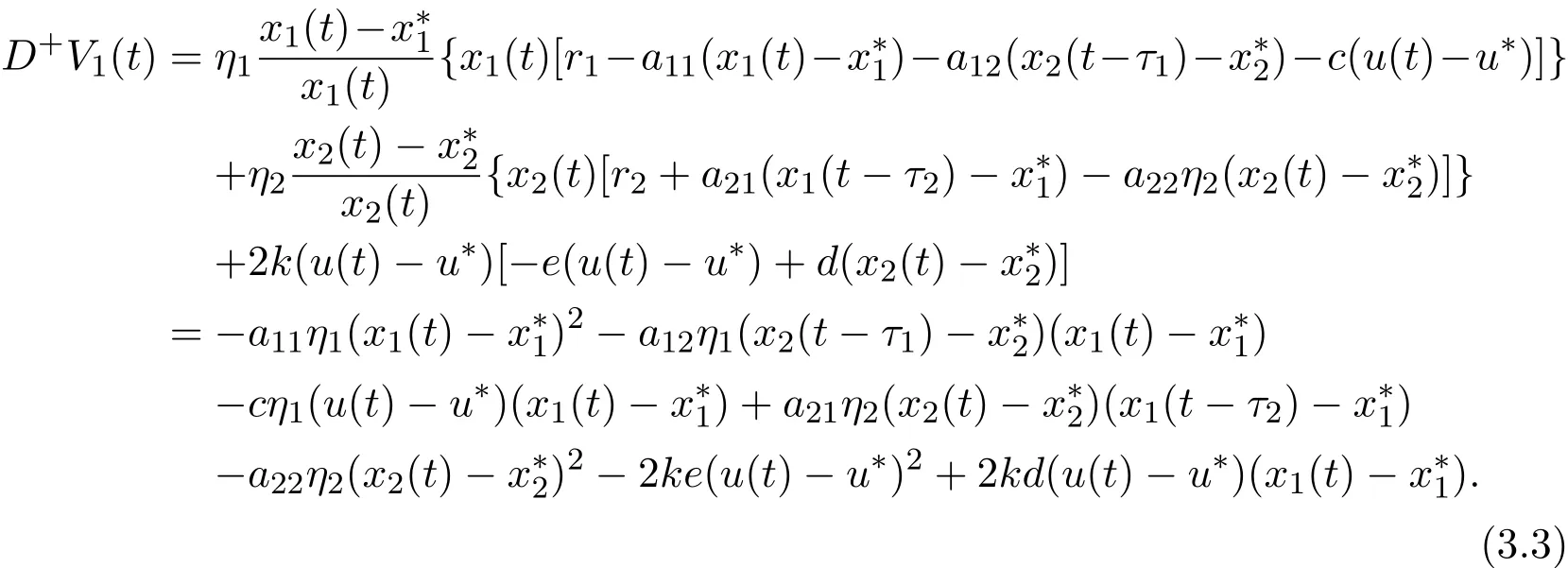
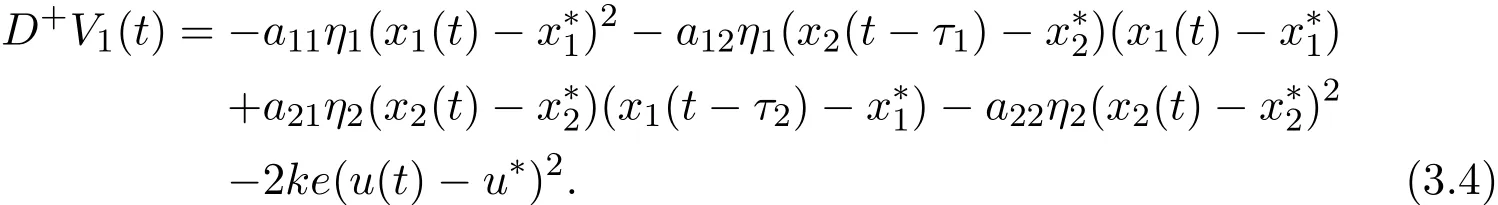
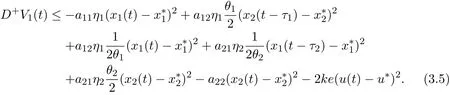
Let

Calculating the derivative of V2(t),we obtain

Define V(t)=V1(t)+V2(t),then we have
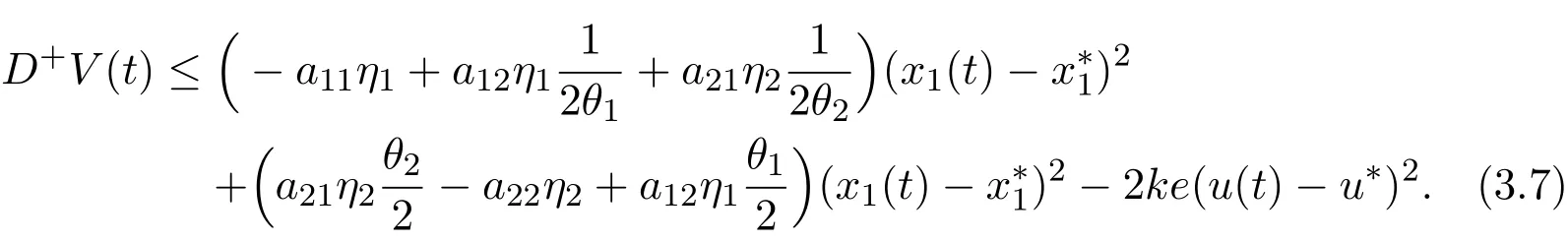
Denoting
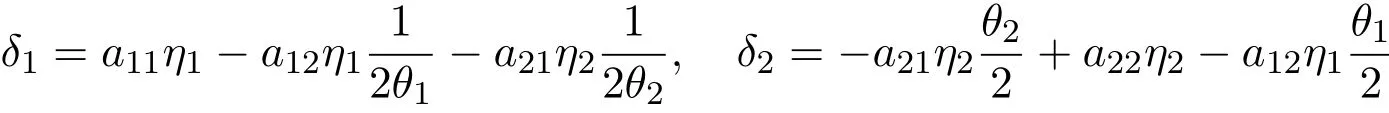
and letting η1=1,η2=,θ1= θ2=,we have
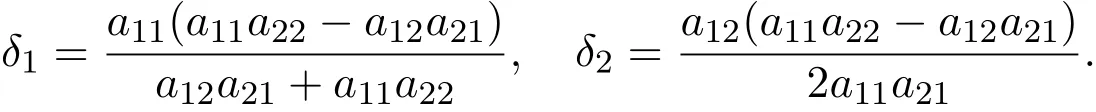
Then,a11a22− a12a21>0 shows that δi>0,i=1,2.It is easy to see that

Therefore,V(t)is nonincreasing.
By Lemma 2.1,xi(t)(i=1,2)are bounded,so xi(t)−are uniformly continuous on[0,+∞).Integrating both sides of(3.8)on the interval[T,t),we have
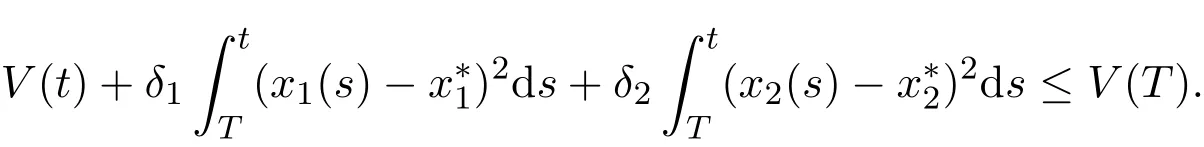
It follows from Lemma 2.1 and the initial condition that xi(t)(i=1,2)are bounded for t∈R,then there exists an M>0 such that 0 Therefore It follows that(xi(s)−)2∈ L1[0,+∞),i=1,2.By Barbalat’s lemma,we have By the third equation of system(1.4)we have This completes the proof of Theorem 3.1.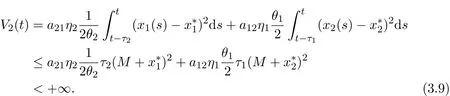
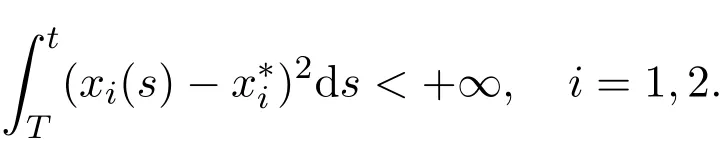
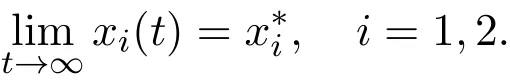
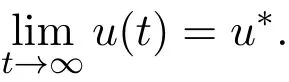
杂志排行
Annals of Applied Mathematics的其它文章
- SOME PROBLEMS OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS IN FIELD THEORY∗
- STABILITY AND BOUNDEDNESS OF SOLUTIONS FOR A CERTAIN FOURTH-ORDER DELAY DIFFERENTIAL EQUATION∗†
- STABILITY ANALYSIS OF A LOTKA-VOLTERRA COMMENSAL SYMBIOSIS MODEL INVOLVING ALLEE EFFECT∗†
- SOME NEW DISCRETE INEQUALITIES OF OPIAL WITH TWO SEQUENCES∗†
- RAMSEY NUMBER OF HYPERGRAPH PATHS∗
- ASYMPTOTIC NORMALITY OF THE NONPARAMETRIC KERNEL ESTIMATION OF THE CONDITIONAL HAZARD FUNCTION FOR LEFT-TRUNCATED AND DEPENDENT DATA∗†
