STABILITY AND BOUNDEDNESS OF SOLUTIONS FOR A CERTAIN FOURTH-ORDER DELAY DIFFERENTIAL EQUATION∗†
2019-01-09MeilanCaiFanweiMeng
Meilan Cai,Fanwei Meng
(School of Mathematical Sciences,Qufu Normal University,Qufu 273165,Shandong,PR China)
Abstract In this paper,with the help of Lyapunov functional approach,sufficient conditions for the asymptotic stability of zero solution for a certain fourthorder non-linear delay differential equation are given.
Keywords Lyapunov functional approach;asymptotic stability;fourthorder non-linear delay differential equation
1 Introduction
As we know,the stability of zero solution plays an important role in the theory and applications of differential equations.In recent decades,by constructing Lyapunov functions or functionals many results have been obtained on the behaviour of solutions for higher order non-linear ordinary differential equations or higher order non-linear differential equations with delay,see[1-12,14-16].However,it is worth noting that there are only a few papers on the stability of solutions for certain fourth order non-linear differential equations with delay.
In[1],Sinha investigated the asymptotic behaviour of the solutions for a nonlinear differential equations with finite lag
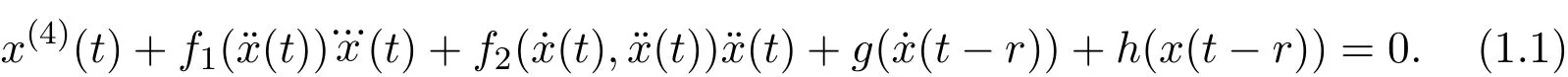
In[2],Tunc considered a fourth-order non-linear delay differential equation

and gave the asymptotic stability of solutions for(1.2).
In[3],the authors studied the fourth-order delay differential equation of the form
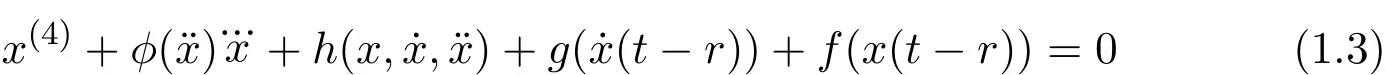
and obtained sufficient conditions for the asymptotic stability of solutions.
In this paper,we investigate the same problem for the following fourth-order non-linear delay differential equation
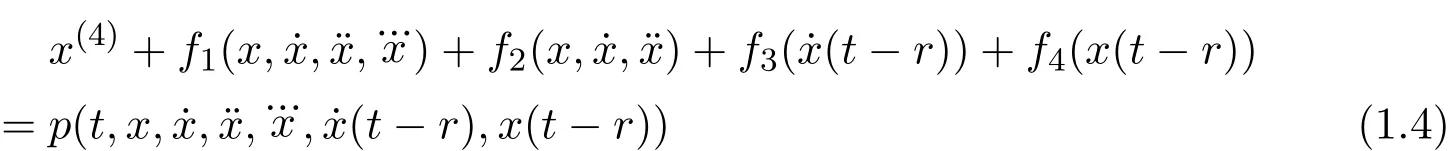
by constructing a new Lyapunov functional,where r is a positive constant,and f4(x)are continuous differential functions and f2(0,0,0)=f3(0)=f4(0)=0,where we assume that the derivativesandexist and are continuous for all x,y,z.The dots indicate differentiation with respect to t.
2 Preliminaries
Before giving the main result of this paper we need the following definitions and stability criteria for the general autonomous delay differential system.We consider

where f:CH→ Rnis a continuous mapping with f(0)=0,CH={ϕ∈C([−r,0],Rn):∥ϕ∥≤ H}and for H1
Definition 2.1[2-4]An element Ψ ∈ CHis in the ω-limit set of ϕ,say,Ω(ϕ),if x(t,0,ϕ)is defined on[0,∞)and there is a sequence{tn}with tn→∞ as n→∞,such that∥xtn(ϕ)−Ψ∥→ 0 as n → ∞,where xtn(ϕ)=x(tn+θ,0,ϕ)for−r≤ θ≤ 0.
Definition 2.2[2-4]A set Q ⊂ CHis an invariant set if for any ϕ ∈ Q,the solution x(t,0,ϕ)for(2.1)is defined on[0,∞),and xt(ϕ)∈ Q for t∈ [0,∞).
Lemma 2.1[2-4]Ifϕ ∈ CHsatisfies that the solutionxt(ϕ)for(2.1)withx0(ϕ)=ϕis defined on[0,∞)and∥xt(ϕ)∥ ≤ H1≤ Hfort∈ [0,∞),thenΩ(ϕ)is a nonempty,compact,invariant set anddist(xt(ϕ),Ω(ϕ))→ 0ast→ ∞.
Lemma 2.2[2-4]LetV:CH→Rbe a continuous functional satisfying a local Lipschitz condition,V(0)=0and that
(i)W1(|ϕ(0)|)≤ V(ϕ)≤ W2(∥ϕ∥)whereW1(r)andW2(r)are wedges;
Then the zero solution for(2.1)is uniformly stable.If we defineZ={ϕ ∈ CH:=0},then the zero solution for(2.1)is asymptotically stable,provided that the largest invariant set inZisQ={0}.
Theorem 2.1[13]LetSandS1be open convex subsets ofX,S0be a closed convex subset ofXwithS0⊂S1⊂S,fbe a compact mapping of S intoX.Supposethat for a positive integerm,fmis well-defined onS1with,whilefm(S1)⊂S0.Thenfhas a fixed point inS0.
Theorem 2.1 is the famous Browder′s fixed point theorem.
3 Main Results
It is obvious that equation(1.4)is equivalent to the following system

First,let

Assume p(t,x,y,z,u,x(t−r),y(t−r))=0,then we get the following theorem.
Theorem 3.1In addition to the fundamental assumptions imposed onf1,f2,f3,andf4,we suppose that there exist positive constantsa,b,c,d, δandε,such that for everyx,y,z,uin,the following conditions are satisfied:

Then the zero solution for system(3.1)is asymptotically stable,provided that

with

Remark 3.1 From conditions(i)and(iii)we can easily obtain

Proof We introduce a Lyapunov function of system(3.1)defined by

where λ and µ are positive constants which will be determined below.
It is easy to see that V(0,0,0,0)=0.We find that the expression of 2V can be rewritten in the following form
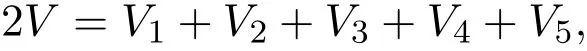
where
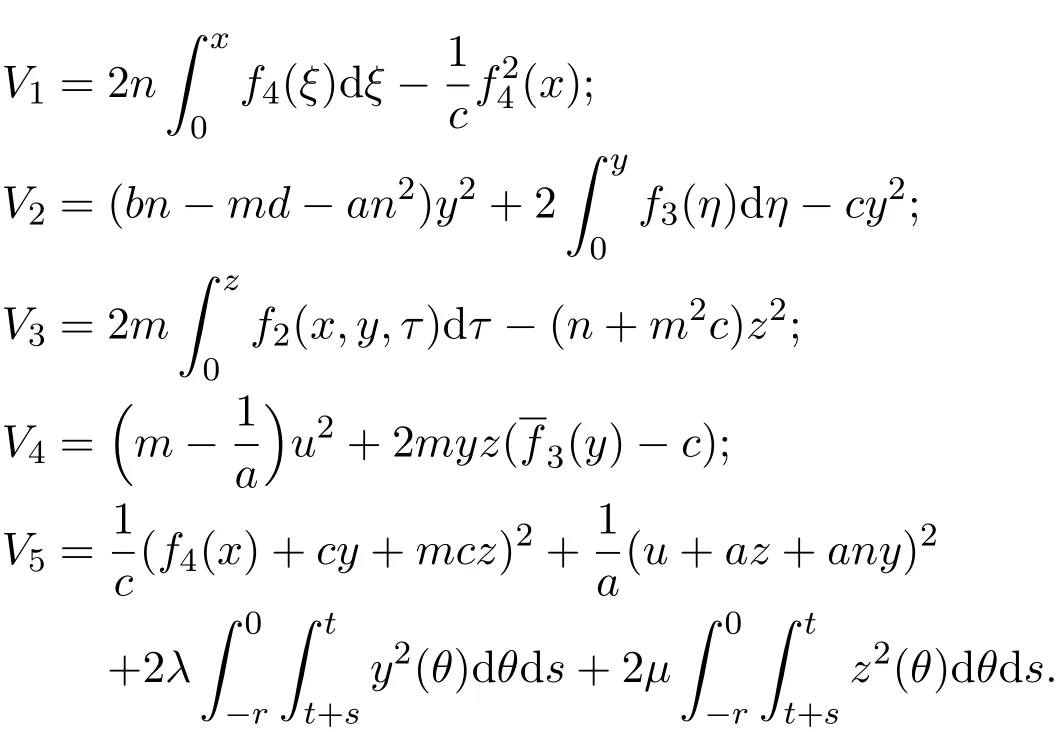
According to the differential and integral mean value theorem and conditions(ii),(iii),we get

By conditions(i),(iii)and(3.5),we have
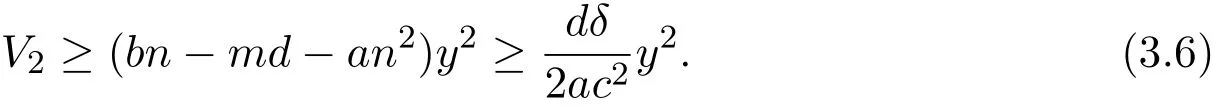
From conditions(i)and(iv),we get

By condition(iii),we get

Thus
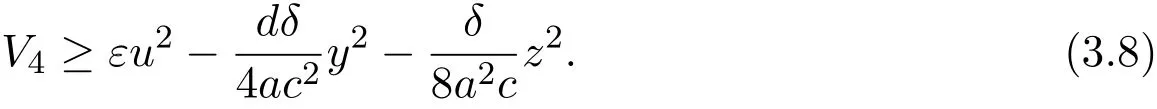
According to the above discussion,we have

Therefore,it is easy to see that V satisfies condition(i)of Lemma 2.2.By the identity

for direct calculation,we get the total derivative of(3.3)with respect to t along the solutions of system(3.1)as follows

By conditions(ii)and(iv),we get
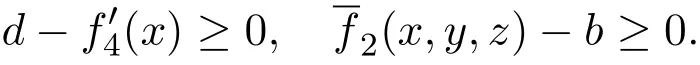
By conditions(iii)and(iv),we obtain
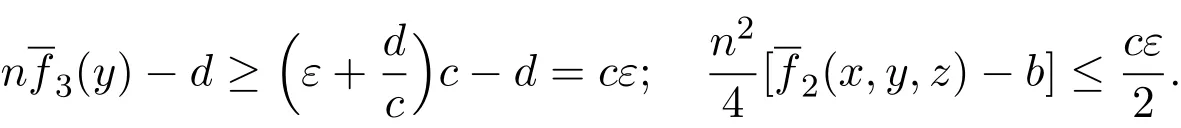
From conditions(i),(ii),(iv)and(3.2),we have
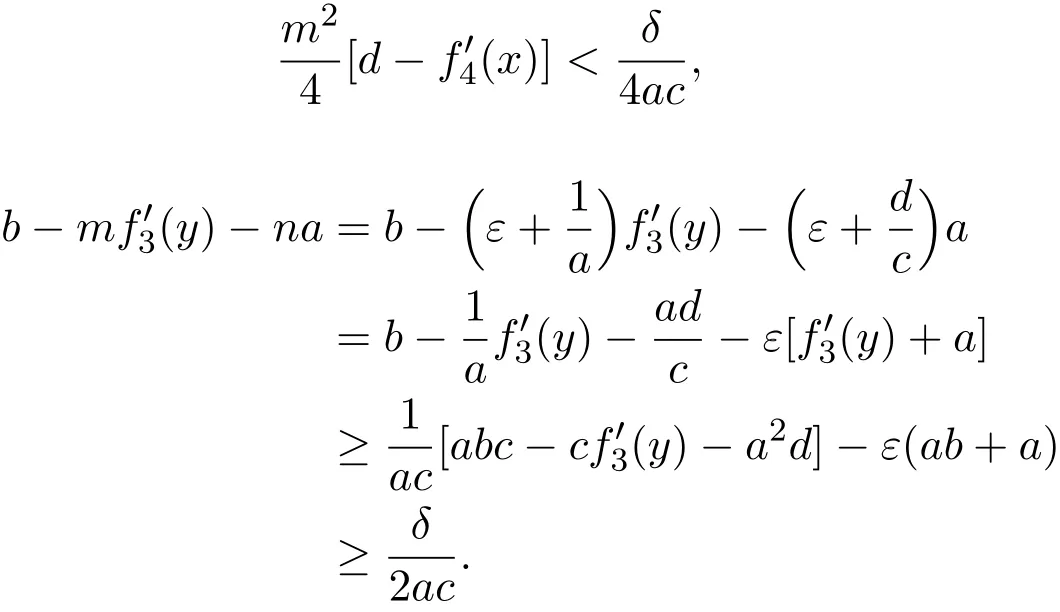
By condition(v),we get
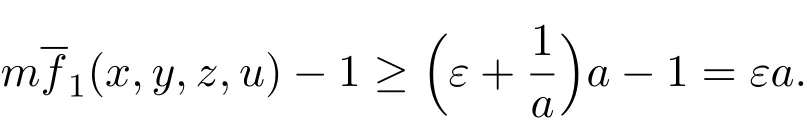
From condition(vi),we have

Based on the above discussion,we can easily get

Now,we let

and
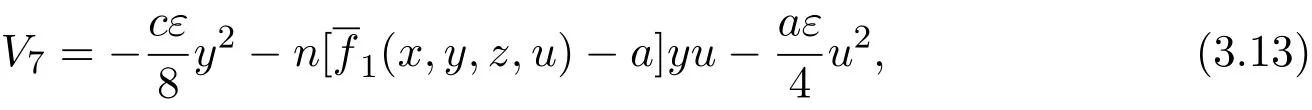
which is contained in equation(3.11).
From condition(v),we get the inequalities

and

then it follows that

Then we obtain


Letting λ=d(m+n+1)/2>0 andµ=ab(m+n+1)/2>0,there is
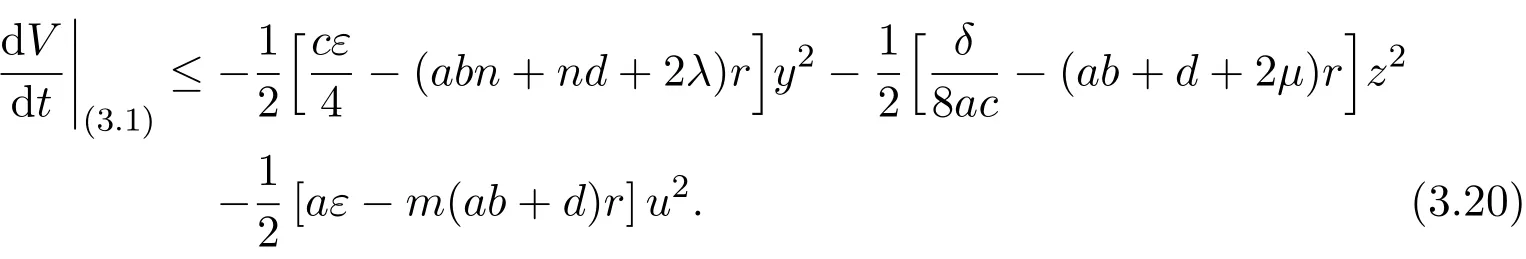
Thus,if

we have
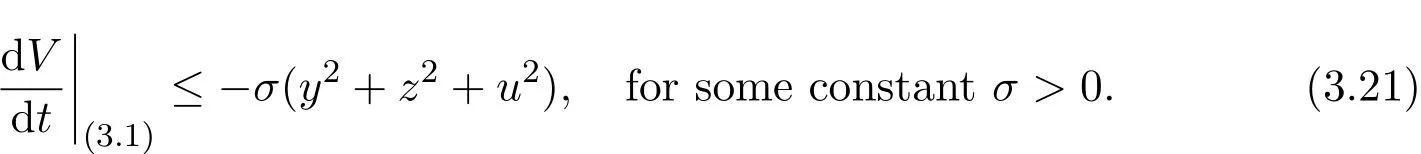
The proof of Theorem 3.1 is now complete.
Let p(t,x,y,z,u,x(t− r),y(t− r))≠0,then we get the following theorems.
Theorem 3.2We suppose that all the conditions of Theorem3.1and

hold,whereq ∈ L1(0,∞)withL1(0,∞)being the space of Lebesgue integrable functions satisfies∫|q(s)|ds≤Q0<∞,andQ0is a positive constant.Then there exists a finite positive constantKsuch that all solutionsx(t)for(1.4)defined by the initial function
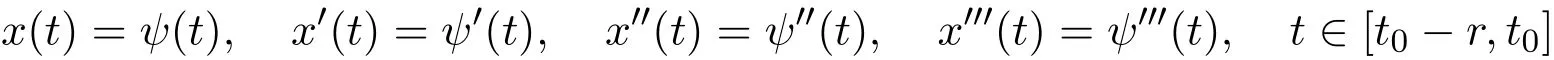
satisfy

for allt≥ t0,whereψ ∈ C3([t0−r,t0],R),provided that

with

Proof From(3.9)we have

where
According to(3.21),we obtain

where D2=max{m,n,1}.
Making use of inequalities|y|<1+y2,|z|<1+z2and|u|<1+u2,it is obvious that

By(3.22),we get

Therefore,
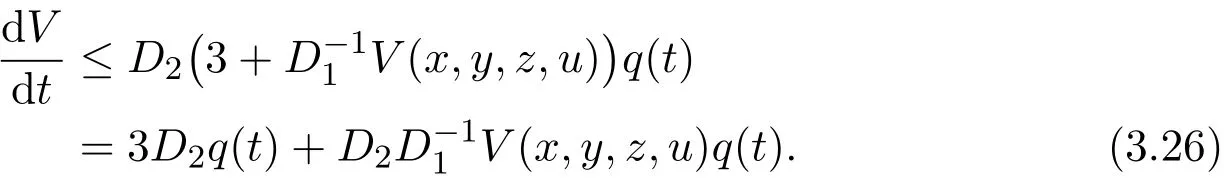
Now,integrating inequality(3.26)from 0 to t,using the condition q∈ L1(0,∞)and Gronwall-Reid-Bellman inequality,we have
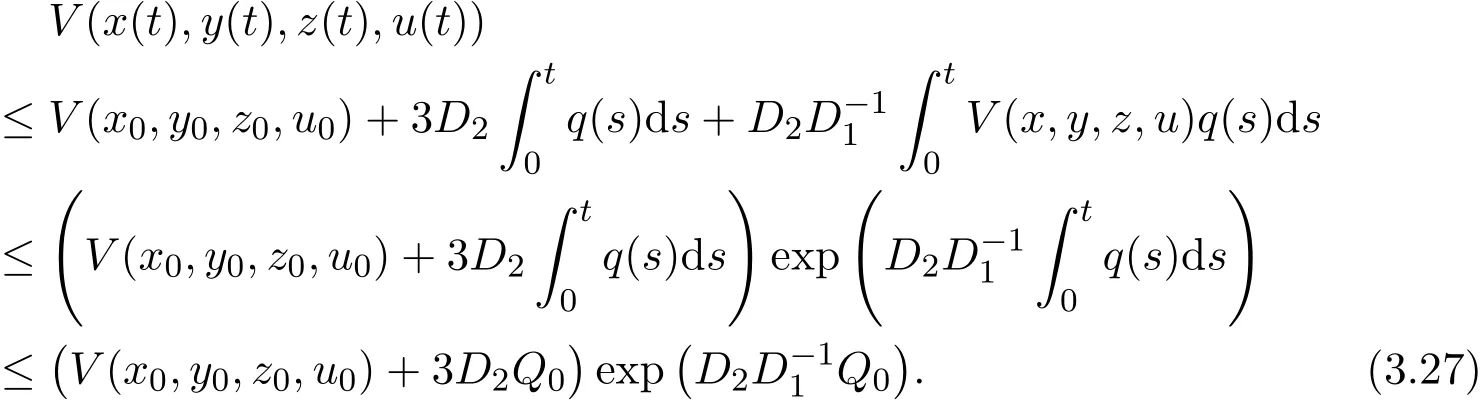
Obviously,the right-hand side is a finite constant,denoted as K1.
By inequalities(3.22)and(3.27),we have

where K2=.Therefore,we can deduce that
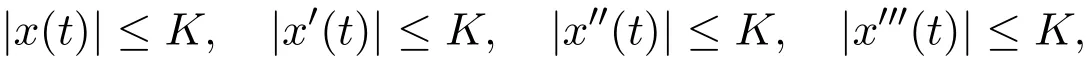
for all t≥t0.
The proof of Theorem 3.2 is completed.
Theorem 3.3In addition to the conditions of Theorem3.1,we also assume that there exist continuous functionsθ1(t)andθ2(t),such thatp(t,x,y,z,u,v,w)satisfies

uniformly int≥ 0,whereθ1(t)andθ2(t)satisfy
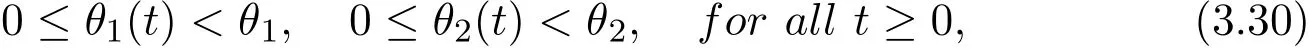
andis sufficiently small.Then the solutions of system(3.1)are uniformly ultimately bounded.
Proof Since p(t,x,y,z,u,v,w)satisfies(3.29),by(3.21)and Schwarz′s inequality we have

By(3.30),we have

and

Then
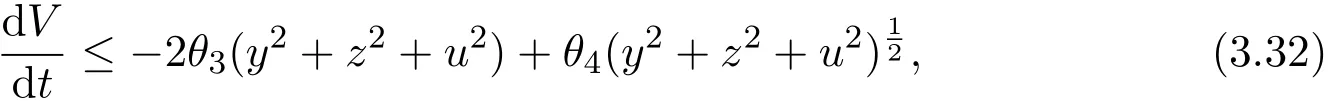
where


By Theorem 3.1 and Theorem 8.10 in Yoshizawa[17],solutions of(3.1)are uniformly ultimately bounded.
The proof of Theorem 3.3 is completed.
Theorem 3.4We assume that all the conditions of Theorem3.3are satisfied,and thatp(t,x,y,z,u,v,w)satisfies

then there exists at least oneω-periodic solution for(3.1).
Proof By the Theorem 3.3,we obtain that all solutions for(3.1)are uniformly ultimately bounded for bound M(M≥K).
Consider the Poincaré map

Since the solution of(3.1)are uniformly bounded,there exists a q(M)>0,such that if t0∈ I=[0,∞)and(x0,y0,z0,u0)∈,where
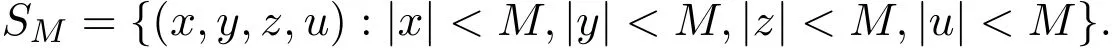
Then

Similarly,there exist two constant r and r∗such that if t0∈ I and(x0,y0,z0,u0)∈with Sq={(x,y,z,u):|x| and if t0∈I,(x0,y0,z0,u0)∈with Sr={(x,y,z,u):|x| Let S=Sr,then T(S)⊂∗and T is continuous.Thus,T is a compact mapping. Since solutions of(3.1)are uniform-ultimately bounded for bound M,there exists a τ>0,such that if t≥ τ and(x0,y0,z0,u0)∈ Sq,then Then there exists a positive integer m such that for(x0,y0,z0,u0)∈Sq. According to Theorem 2.1,the Poincaré map T has a fixed point(x0,y0,z0,u0)in,that is, The proof of Theorem 3.4 is completed. Remark 3.2 Theorems 3.1 and 3.2 are different with Theorems 3.1 and 3.3 in[14],respectively.Furthermore,the results of Theorems 3.3 and 3.4 only be studied in this paper.

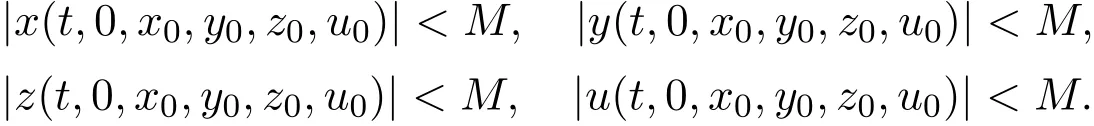

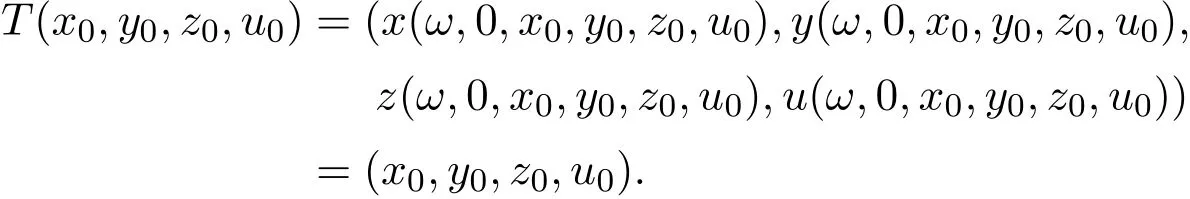
杂志排行
Annals of Applied Mathematics的其它文章
- SOME PROBLEMS OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS IN FIELD THEORY∗
- A LOTKA-VOLTERRA PREY-PREDATOR SYSTEM WITH FEEDBACK CONTROL EFFECT∗
- STABILITY ANALYSIS OF A LOTKA-VOLTERRA COMMENSAL SYMBIOSIS MODEL INVOLVING ALLEE EFFECT∗†
- SOME NEW DISCRETE INEQUALITIES OF OPIAL WITH TWO SEQUENCES∗†
- RAMSEY NUMBER OF HYPERGRAPH PATHS∗
- ASYMPTOTIC NORMALITY OF THE NONPARAMETRIC KERNEL ESTIMATION OF THE CONDITIONAL HAZARD FUNCTION FOR LEFT-TRUNCATED AND DEPENDENT DATA∗†
