小药量内爆情况下双壳体碎片飞散速度的理论分析
2019-01-08卢芳云李翔城文学军
卢芳云,李翔城,文学军,陈 荣,曹 雷
(1.国防科技大学 文理学院,长沙410073;2.火箭军研究院,北京100085;3.武警后勤学院,天津300309)
分离装置是运载火箭重要的组成部分之一[1]。分离装置在分离之前承担连接功能,在分离信号到达之后承担解锁和分离功能,其功能的实现与否直接关系到发射任务的成败。火工分离装置具有可靠性高、同步性好的优点,是目前应用最广泛的一类分离装置[2]。柔爆索(mild detonating fuse, MDF)分离装置是火工分离装置的一种, 在大型运载火箭或导弹系统上,在级间分离、星箭分离、卫星整流罩分离等具有大直径或长分离面的场合下,柔爆索分离装置表现出了明显的优势[3-4]。
图1为柔爆索分离装置截面图。从图1可以看出:柔爆索位于分离装置截面的中间,柔爆索爆炸后,分离板和保护罩受爆轰气体高压作用发生膨胀变形,导致分离板碎裂,实现结构分离,而这时保护罩起到保护箭体内部设施完好的作用。在这个过程中,分离碎片能否可靠地飞离箭体,关系到火箭主体后续飞行的安全性。因此,研究柔爆索爆炸做功的分离碎片的飞散特性尤为重要。
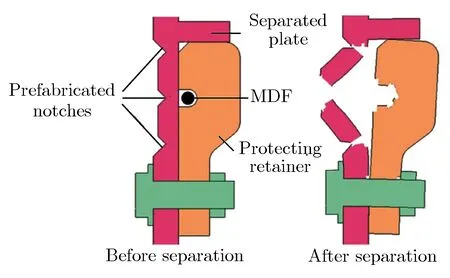
图1柔爆索分离装置截面图 Fig.1Sectional diagram of MDF separating unit
对于轴对称结构内部爆炸导致材料碎裂的现象, Mott在二战时期就开展了开创性研究[6];Grady等针对金属、岩石及特种材料做了大量实验研究,从破坏机理上对内爆载荷下材料的碎裂现象进行了理论分析[7];李永池等分析了内爆载荷下圆管的变形、损伤和破坏规律[8]。Gurney 基于爆炸过程中的能量守恒,分析导出了壳体碎片运动速度的计算公式[9],即著名的Gurney公式。利用该公式可以分析轴对称结构内部爆炸驱动壳体的变形和运动问题。Gurney公式在工程实践中得到了广泛应用,尤其是估算破片战斗部的破片速度是比较准确的[9]。爆炸分离装置的作用过程是内部柔爆索爆炸作用下的结构响应过程,这个作用过程与典型的内部爆炸结构(如破片战斗部)的过程类似。与破片战斗部不同之处在于柔爆索的装药量很小,而柔爆索驱动的外部结构质量很大且从结构上看能量释放过程中几何上不对称。如果不考虑结构的不对称性,Gurney公式在装药比为0.1~10[10]的范围内适用,而分离装置中的装药比约为0.01,远低于Gurney公式适用的最小装药比。因此需要慎重采用Gurney公式来研究分离碎片的飞散特性[10]。
本文考察在小药量和双层壳体情况下求解壳体的飞散速度问题。柔爆索本身就是一个内爆结构,柔爆索爆炸将引起柔爆索外的铅层膨胀变形而获得运动速度,构成了第1阶段;之后,柔爆索的外壳作用于外围结构,如分离板,外围结构膨胀获得整体的运动速度,此为第2阶段;最后,柔爆索破裂,爆轰产物持续做功,结构碎片达到最终的飞散速度,此为第3阶段。本文设计了轴对称圆筒结构模拟对称结构的分离装置,探索了3个理论途径,分阶段建立柔爆索爆炸驱动外围结构的运动速度计算模型。理论计算结果最终与相应的实验结果和数值模拟结果进行了比较,论证了不同理论模型的适用性。
1 圆筒计算模型
1.1 柔爆索性能
采用的柔爆索由中国兵器工业集团804厂生产,它是一种在航天和兵器工业中普遍使用的火工品。柔爆索的中心为装药药芯,药芯外面包覆有一层铅层,如图2所示。
黑索金(RDX)药芯直径2r0为1.68 mm;柔爆索直径d0为2.94 mm;RDX和铅层密度分别为1.42 g·cm-3和11.06 g·cm-3;l为柔爆索长度。计算得到RDX单位长度质量mex为3.12×10-3g·mm-1,铅层单位长度质量mpb为5×10-2g·mm-1。
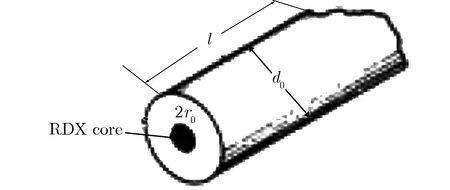
图2柔爆索结构示意图[9]Fig.2Structural diagram of MDF [9]
利用Kamlet模型[11]计算炸药的爆压与爆速:
(1)
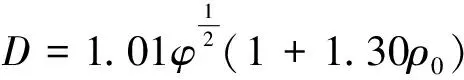
(2)
(3)
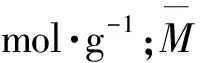
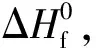
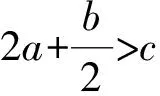
M=12a+b+16c+14d
(4)
(5)
(6)
(7)
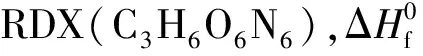
C3H6O6N6→3N2+3H2O+1.5CO2+1.5C
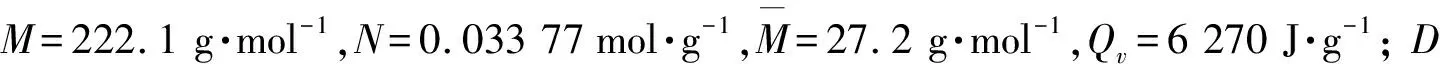
1.2 圆筒几何模型
为了研究柔爆索爆炸驱动碎片的飞散参数,设计了12种不同尺寸的厚壁圆筒预制碎片,预制碎片采用45#钢。柔爆索爆炸驱动模型截面示意图,如图3所示。截面几何参数如表1所列。其中,装药比为
(8)
式中,M0为外围壳体单位长度的质量。
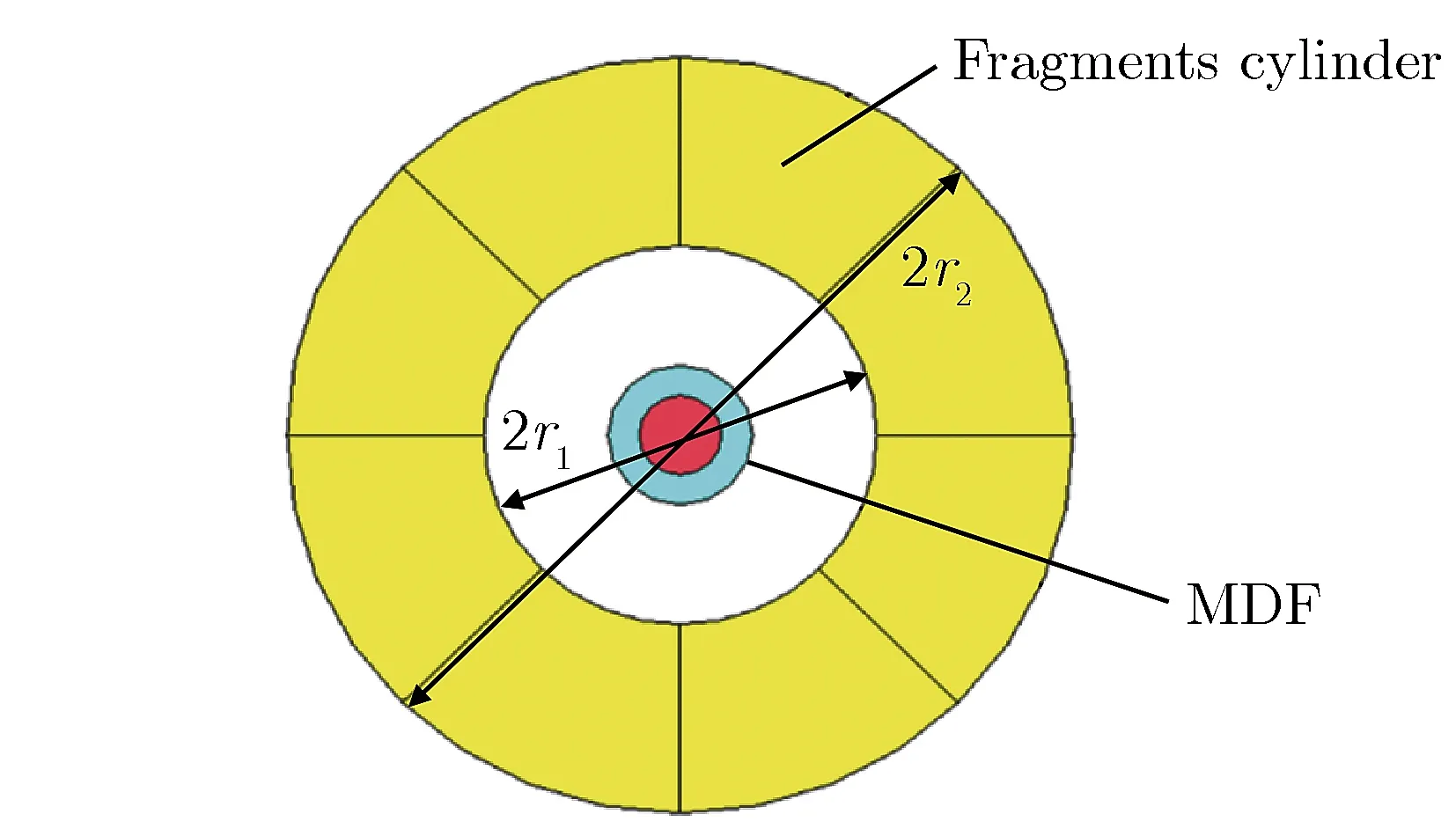
图3柔爆索爆炸驱动模型截面示意图Fig.3Schematic of MDF explosion driving geometry
Tab.1Structuralparametersoffragmentforthethickwallcylinder
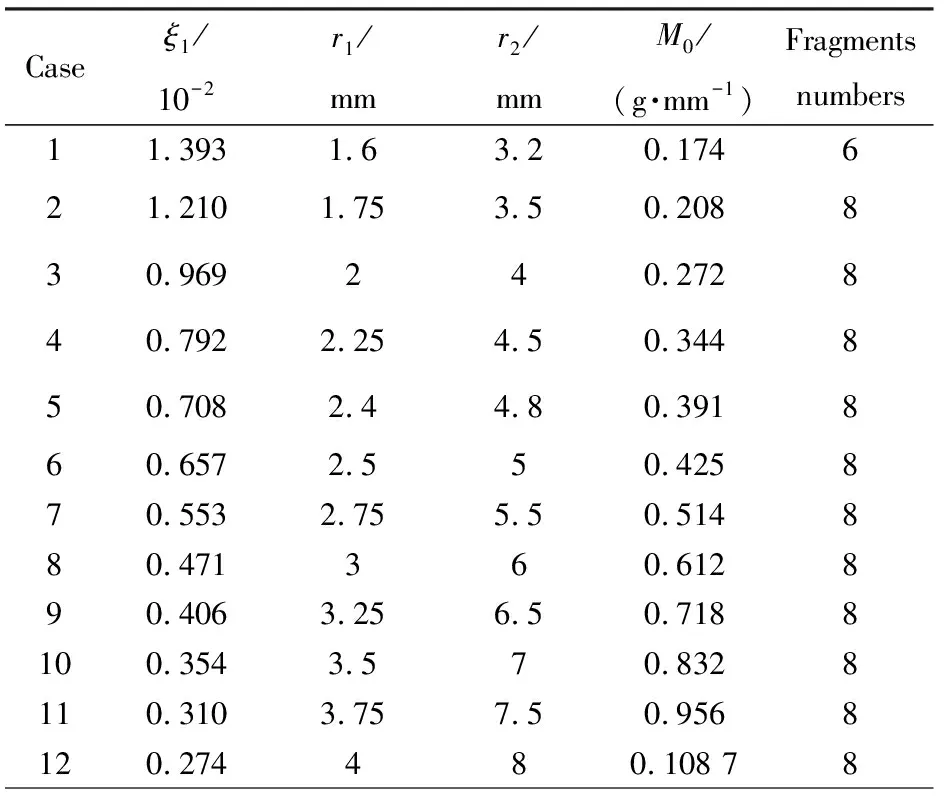
Caseξ1/10-2r1/mmr2/mmM0/(g·mm-1)Fragmentsnumbers11.3931.63.20.174621.2101.753.50.208830.969240.272840.7922.254.50.344850.7082.44.80.391860.6572.550.425870.5532.755.50.514880.471360.612890.4063.256.50.7188100.3543.570.8328110.3103.757.50.9568120.274480.108 78
2 理论分析模型
针对图3所示的结构,将碎片飞散获得速度的过程分为3个阶段。第1阶段:柔爆索爆炸引起柔爆索铅层壳体膨胀变形获得运动速度v0;第2阶段:柔爆索外壳膨胀作用于外围预制碎片,使之获得一个瞬时初速v1;第3阶段:柔爆索破裂后爆轰产物持续做功,推动碎片获得一个速度增量vi,最终碎片达到飞散速度v=v1+vi。
2.1 第1阶段速度v0
第1阶段铅层飞散速度v0的计算,利用以下3个模型:
模型1:将柔爆索驱动铅层壳体看作圆柱形装药结构,根据Gurney公式计算出铅层的飞散速度v0。这时,炸药能量转化为壳层和爆轰产物的动能,装药比ξ2采用柔爆索中装药质量mex与铅层质量mpb之比,计算公式为
(9)
其中,在工程计算中,炸药的古尼能可以用爆热Qv代替;装药比ξ2=mex/mpb。
模型2:铅层与外围预制碎片一起作为爆炸驱动的整体,即,ξ1为柔爆索中装药质量mex与铅层和壳体质量之和(mpb+M0)的比值。利用Gurney公式计算铅层和壳体作为整体的飞散速度v0,则
(10)
其中,装药比ξ1=mex/(mpb+M0)。该模型相当于不区分第1和第2个阶段,因此第2阶段的瞬时速度v1=v0。
模型3:由于爆轰产物的爆热难以估算,为此,模型3考虑用动量守恒的方法,建立第1阶段的速度v0计算模型。
柔爆索铅层壳体在爆轰产物的推动下向外膨胀加速,其运动方程为
(11)
式中,vs为铅层飞散的实时速度;p为柔爆索内爆轰产物的压力。铅层的内壁就是爆轰产物膨胀的边界:
dr=vsdt
(12)
联立式(11)和式(12),铅层加速过程的运动方程可写为
(13)
式中,r0为铅层内壁的初始半径;r1为碎片内壁的半径;v0为铅层膨胀到碎片边界时达到的速度,这里忽略了铅层最终的厚度。对爆轰产物采用简化的多方气体膨胀状态方程pVlk为常数,这里,k为多方指数。由于单位长度爆轰产物体积Vl=πr2,状态方程可表达成爆轰产物半径的形式,于是式(13)中爆轰产物压力p也可表示成爆轰产物半径r的函数:
(14)
式中,rk是指爆轰产物压力为特征压力pk时相应的爆轰产物半径。考虑爆轰产物膨胀过程中多方指数k将发生变化,这里,作简化处理,取两个值,分别为k1和k2。特征压力pk定义为多方指数发生突变时的压力[10]。假定爆轰产物初始压力p0为爆轰产物压力的一半,联立式(13)和式(14),通过半径r将爆轰产物压力p表示为
(15)
式中,vk是指爆轰产物压力为pk时对应的碎片速度。可以看出:铅层速度vs是爆轰产物半径rk的一元函数,即,在爆轰产物推动铅层加速过程中,任一时刻的铅层速度都可以定量求解,铅层速度vs的最终峰值为v0。
2.2 第2阶段速度v1
对于模型2,v1=v0。对于模型1和模型3,考虑第2阶段的驱动过程,认为膨胀的铅层高速碰撞外围碎片,使碎片获得瞬时速度v1。碰撞的性质是未知的,估计可能介于完全非弹性和完全弹性之间。
当碰撞为完全非弹性时,铅层附着于碎片内壁,碰撞后,二者具有相同的速度。根据动量守恒定律:
mpbv0=(mpb+M0)v1
(16)
碎片获得的瞬时速度为
(17)
当碰撞为完全弹性时,碰撞后,二者的速度是不同的,如果碰撞后铅层的速度用v′表示,则根据过程中动量和能量守恒,得到
mpbv0=mpbv′+M0v1
(18)
可解出碎片的瞬时速度为
(19)
可见,完全弹性碰撞下的碎片速度是完全非弹性碰撞下碎片速度的2倍。为此,引入碰撞系数λ来定量表征铅层与碎片之间的碰撞性质。λ取值为1~2,1代表完全非弹性碰撞,2代表完全弹性碰撞。实际情况下碎片瞬时速度为
(20)
通过将计算结果与数值模拟结果对比发现,当λ取1.55时,理论计算的结量与数值计算结果符合较好。
2.3 第3阶段速度增量vi
碎片获得瞬时速度之后往向外飞散,管状铅层破裂,爆轰产物继续推动碎片运动,碎片迎风面为碎片的外表面。碎片运动方程为
(21)
式中,r2为碎片外壁半径。假设爆轰产物以碰撞时刻的速度v0稳定向外膨胀,即
dr=v0dt
(22)
直至其压力降低为环境气压:
pairrinf2k2=pkrk2k2
(23)
式中,pair和rinf分别为环境气压和此时的爆轰产物半径。联立式(21)--式(23),可求出碎片第3阶段的速度增量vi:
(24)
3 计算结果与分析
3.1 典型工况结果比较
对表1中12种不同尺寸的圆筒工况进行了数值仿真,其中,装药RDX利用JWL状态方程式(25)描述。RDX装药的状态方程材料参数如表2所列。模拟计算得到的碎片速度时程曲线,如图4所示。
(25)
式中,R1,R2,ω均为经验参数。
表2RDX装药的状态方程材料参数
Tab.2MaterialEOSparametersofRDX
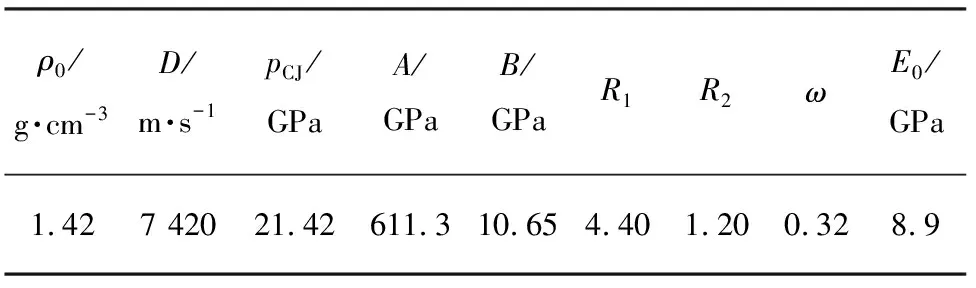
ρ0/g·cm-3D/m·s-1pCJ/GPaA/GPaB/GPaR1R2ωE0/GPa1.427 42021.42611.310.654.401.200.328.9
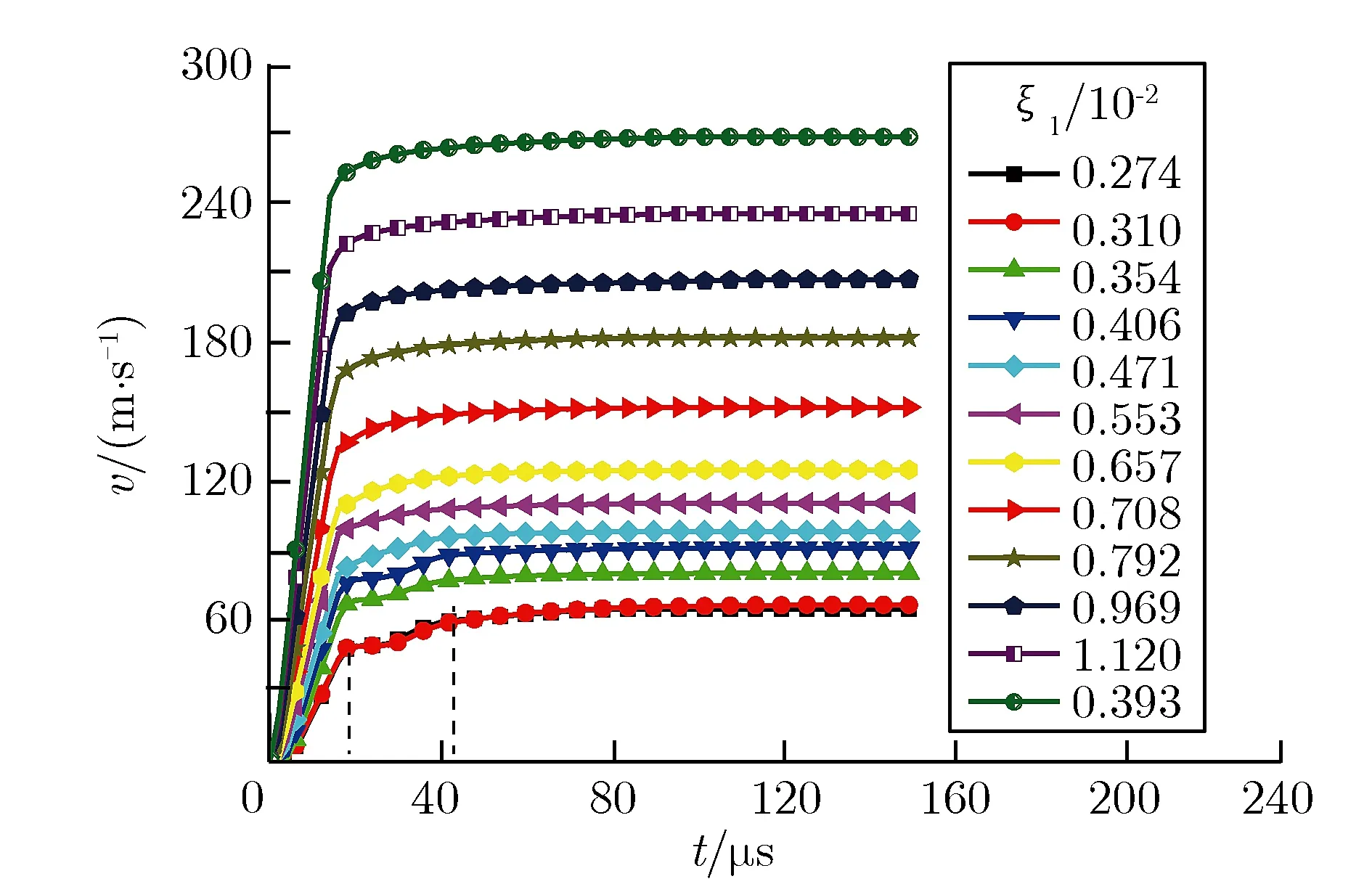
图4圆筒内爆碎片时程曲线Fig.4Velocity of cylinder fragments vs. time
由图4可知,柔爆索爆炸推动碎片的加速过程可以分为铅层撞击加速段(对应理论模型的第1和第2阶段)和产物推动加速段(第3阶段)2个阶段。这在一定程度上证明了模型分析的正确性。
对表1中的工况1和工况12进行实验,并将实验结果与相应的数值模拟结果进行对比,结果如表3所列。表3还给出了数值模拟得到的碎片第2阶段瞬时速度v1、第3阶段速度增量vi及最终速度v。针对这两个工况,给出了3个理论模型的相应结果。可以看出,模型2的结果与实验结果偏离较多,而模型1和模型3在装药比很小时的结果都比较接近实验结果,在装药比较大时与实验结果偏离较多。相对而言,模型3的结果整体上更接近实验结果,这表明数值模拟方法是正确的。因此,后续其他工况通过3个理论模型计算的碎片最终速度与数值模拟的相应结果进行比较。
表33种模型的碎片速度比较
Tab.3Comparisonofvelocityoffragmentsamongthreemodels
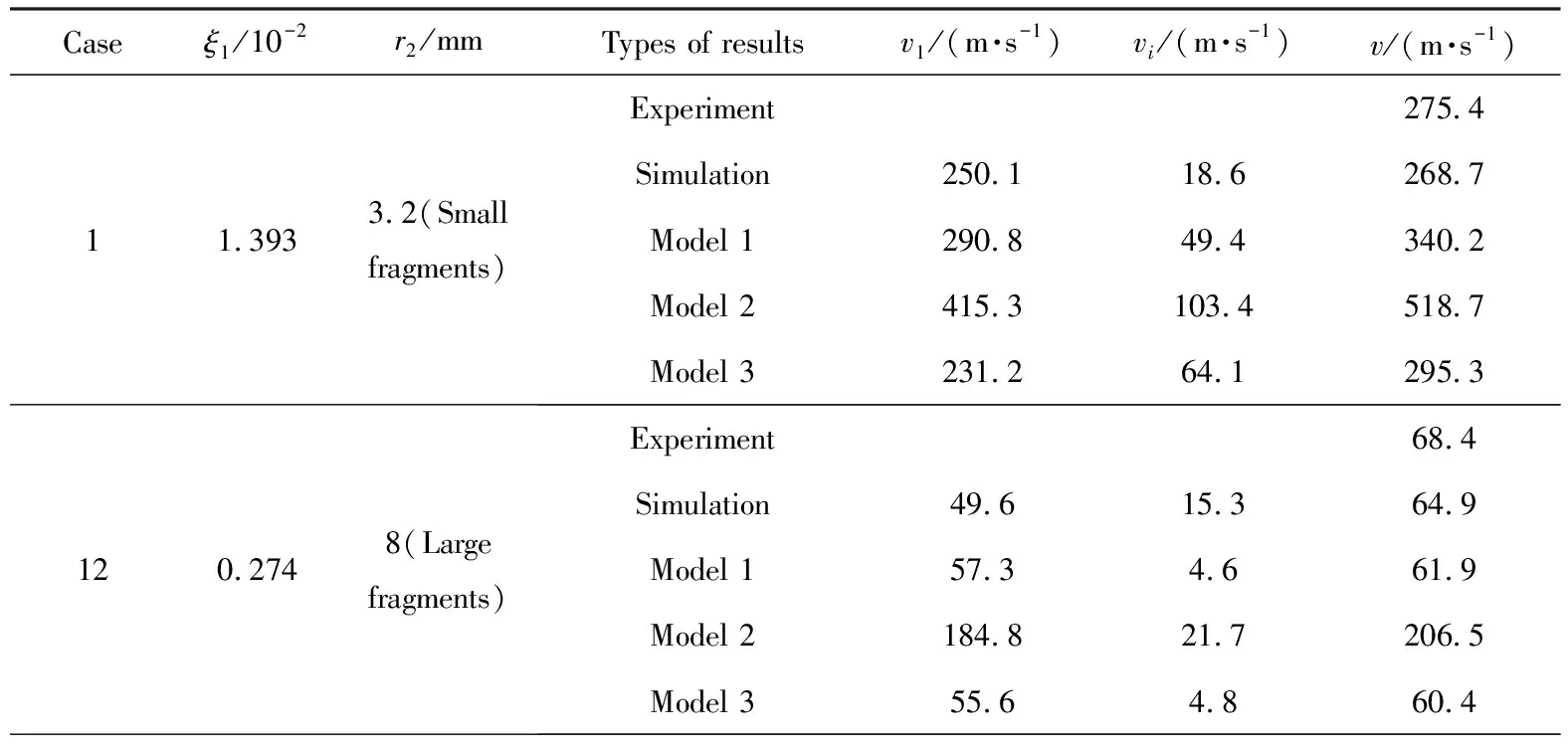
Caseξ1/10-2r2/mmTypes of resultsv1/(m·s-1)vi/(m·s-1)v/(m·s-1)11.3933.2(Smallfragments)Experiment275.4Simulation250.118.6268.7Model 1290.849.4340.2Model 2415.3103.4518.7Model 3231.264.1295.3120.2748(Largefragments)Experiment68.4Simulation49.615.364.9Model 157.34.661.9Model 2184.821.7206.5Model 355.64.860.4
3.2 理论计算结果规律分析
利用3个理论模型计算得到的碎片最终速度随装药比的变化规律,如图5所示。
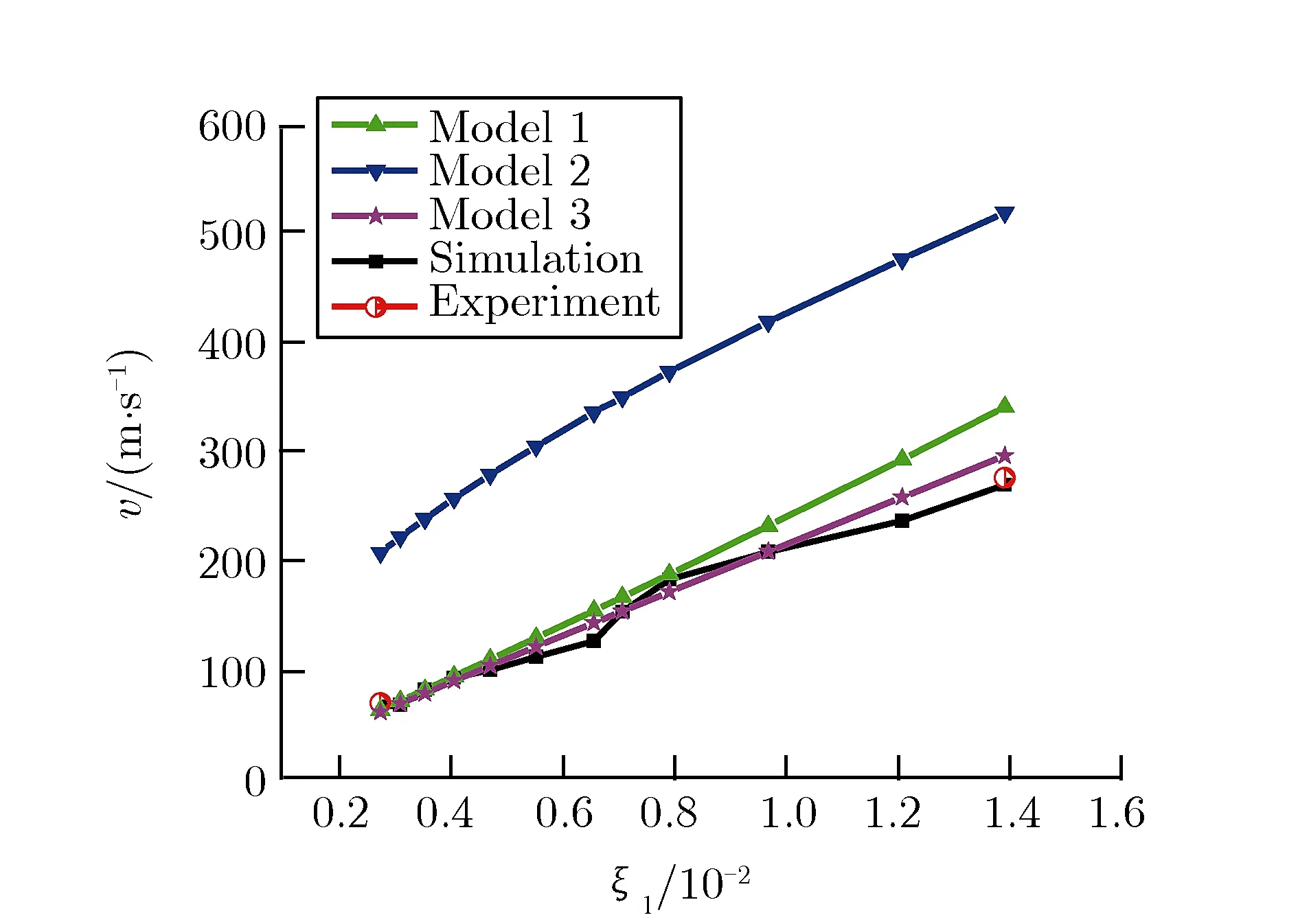
图5碎片最终速度随装药比的变化Fig.5The final velocity vs. the charge ratio
一个有趣的现象是,理论模型得到的速度变化规律是单调光滑的,而数值模拟结果虽然表现出的趋势是总体单调上升,但呈现出两段规律,在装药比为0.657%~0.792%区域内出现了跳跃变化。
如果与数值模拟的结果进行对比,模型2的结果偏离较多,说明Gurney公式在小装药比时的适用性确实值得推敲。而模型1和模型3的实验结果与数值模拟结果很接近,部分有交叉。相对而言,模型3的实验结果整体上更接近数值模拟结果。模型1和模型2都使用了Gurney公式,但二者有两点不同。一是使用Gurney公式时的装药比含义不同。模型1考虑了柔爆索驱动铅层后再撞击外围壳体的两个过程,使用Gurney公式时采用的装药比为柔爆索的装药比,数值为0.062 4,比较接近Gurney公式的适用范围0.1~10,因此,v0的计算是基本准确的;而模型2将两个过程合二为一,这时采用的装药比为表1中所列的值,是0.01或更低,与Gurney公式的适用范围偏离较远;二是模型1考虑了双层壳体的中间撞击过程,而模型2未考虑该中间撞击过程。
模型1和模型3均分阶段考虑了碎片获得的速度,2个模型在装药比很小时,其计算结果十分接近数值模拟结果,装药比稍大时与数值模拟结果偏离较多,这说明两段分析模型具有合理性。同时,模型3的计算结果更接近实验和数值模拟得到数据点,说明动量守恒方法更加科学,因为能量的损失难以理清,带来的误差不便估算,而动量守恒方法可以避免该问题。
比值δ的定义如下:
(26)
计算了3个模型得到的碎片最终速度与数值模拟得到的碎片最终速度之比。3个模型计算得到的装药比比值误差的比较如图6所示。可以看出,模型2确实明显偏离数值模拟结果,而模型1和模型3在跳跃变化的区段(装药比为0.657%~0.792%),理论模型与数值计算相比没有明显的差别。但是随着装药比的增大,模型1和模型3的结果与数值模拟结果之间的偏差越来越大。相对而言,模型3是基于动量守恒的3阶段计算模型,其结果与数值模拟结果最为接近,δ在10%以内。说明,对于小装药比爆炸驱动双层壳体的情况,单纯基于Gurney公式的直接应用要谨慎,发展两段驱动理论模型进行碎片速度的估算是有必要的。
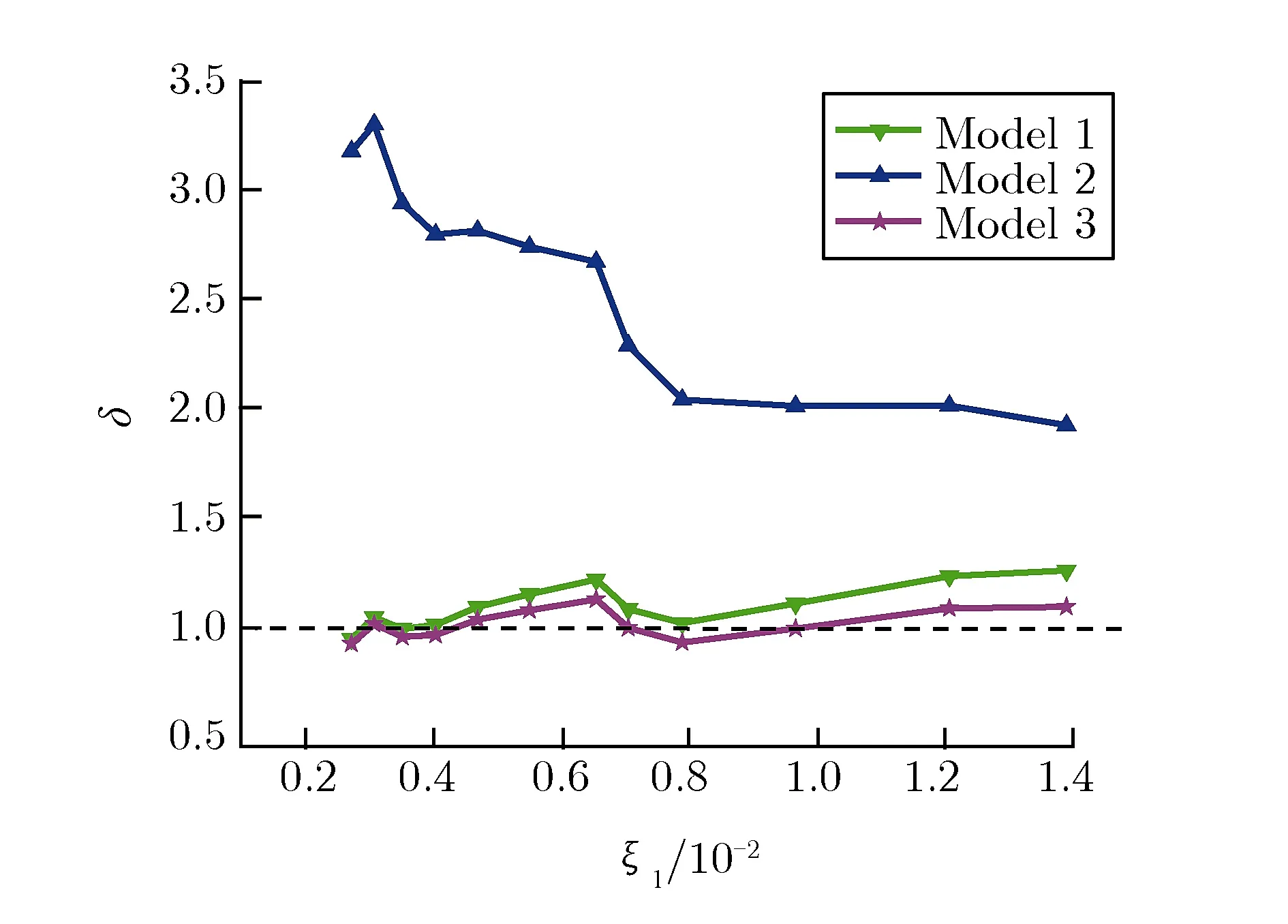
图63种模型计算得到的装药比比值误差比较Fig.6The charge ratio errors calculated by three models
4 结论
本文以柔爆索爆炸加载为研究对象,通过发展理论模型,探索了在小装药比情况下内爆引起双层壳体碎片飞散的速度计算方法,得到以下结论:
1)小装药比爆炸驱动双层壳体的情况下,直接应用Gurney公式计算碎片速度需要谨慎。对于柔爆索爆炸驱动壳体的情况,考虑爆炸驱动的3个阶段计算碎片的飞散速度更符合实验数据和数值模拟计算结果。
2)碎片最终速度由铅层高速撞击获得的瞬时速度和产物继续推动带来的速度增量两部分组成。
本文的研究方法和结论对于小药量爆炸驱动碎片飞散问题研究具有参考价值。然而,目前的理论计算不能反映数值模拟在装药质量比为0.657%~0.792%时,碎片速度出现跳跃变化的现象,其中的机制有待进一步研究。
