介电湿润芯片上液滴从静止到运动的机理
2019-01-08许晓威孙立宁张玉良江海兵
许晓威 孙立宁 张玉良 江海兵
1.衢州学院机械工程学院,衢州,324000 2.苏州大学机器人与微系统研究中心,苏州,215021
0 引言
近年来,微流控技术随着微制作工艺的快速发展取得了很大的突破。在微流控领域中利用介电湿润(electrowetting-on-dielectric, EWOD)机理已经成为一种趋势。目前基于介电湿润机理操控液滴的技术被称为数字微流控技术,包括从储液池中生成液滴、把一个液滴分离成两个子液滴、把两个液滴合并成一个液滴以及液滴的运输四项基本操控[1-4]。数字微流控技术不需要微泵、微阀和微管道等复杂的机械结构,避免了结构复杂部件的制作和装配、不同液体的交叉使用所造成的污染、液体堵死等现象。数字微流控芯片可以操控μL甚至nL级别的单个微液滴,使其在“芯片上实验室”(lab on a chip)中得到越来越多的应用[5-12]。另外,数字微流控技术在光学[13]、芯片降温[14]、传感器[15]等领域也得到了广泛的应用。
数字微流控技术中液滴在电场的作用下经过一系列过程而运动,该过程是多尺度、多阶段的。总结相关文献发现,研究者针对EWOD芯片上液滴从静止到运动的过程和机理提出了各种假设[16-21],而该机理至今未见系统的研究。本文在前人研究的基础上,通过理论分析、数值仿真和实验研究,针对液滴从静止到运动的过程进行研究。
1 介电湿润基本机理
数字微流控技术中常用的结构为图1a所示的“三明治”结构,液滴位于上下极板之间[1,4],施加驱动电压前液滴位于左右驱动电极之上,由于上下极板表面涂有厌水层,液滴的初始接触角θ0接近120°,液滴近似为球形。数字微流控技术操控液滴运动是通过给介电层下方的驱动电极通电来实现的。如图1b所示,液滴由图1a中的近似球形形状变成图1b所示的不规则形状,此时右侧驱动电极通电,液滴的大部分位于左侧不加电驱动电极之上,位于通电驱动电极之上的液滴初始接触角θ0减小,当减小量足够大时,液滴就会向通电驱动电极的方向运动。按时序分别给阵列驱动电极通电,液滴就会按照规划好的路径运动。数字微流控技术包括液滴的生成、分离、合并和运输四项基本操控[1-6]。驱动电压与接触角的关系可由杨-李普曼方程表述:
(1)
式中,θU、θ0分别为液滴在施加驱动电压U时的接触角和不施加驱动电压时的初始接触角;εr、ε0分别为介电湿润芯片介电层的相对介电常数和真空介电常数;γlg为“气-液”表面张力;d为芯片的介电层厚度。
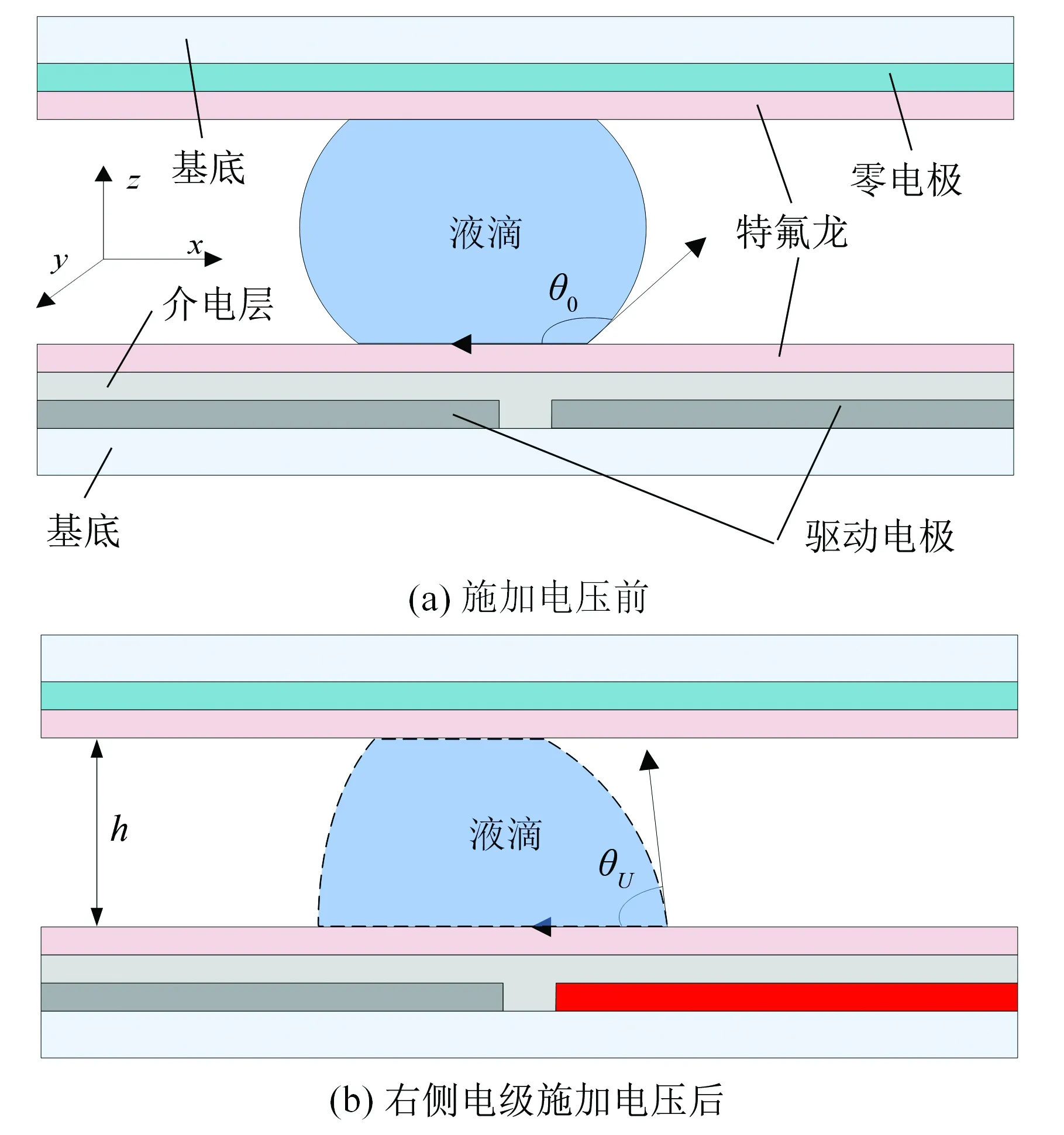
图1 介电湿润基本原理示意图(侧视图)Fig.1 Schematic diagram of electrowetting-on- dielectric basic principle (side view)
2 固液接触面极化机理
在电磁学领域,在外电场作用下,电介质会显示电性。理想的绝缘介质内部没有自由电荷,而实际上,电介质内部总是存在少量的自由电荷,它们是造成电介质漏电的原因。一般情况下,未经电场作用的电介质内部的正负束缚电荷处处抵消,宏观上并不显示电性。而在外电场作用下,束缚电荷的局部移动会导致宏观上显示电性,在电介质的表面和内部非均匀的部分出现电荷,这种现象称为极化,出现的电荷称为极化电荷,这些极化电荷会改变原来的电场。因极化而产生的电偶极子称为“感应电偶极子”,其电偶极矩称为“感应电偶极矩”。电极化强度矢量P也称为电极化矢量,其大小为电介质内的电偶极矩密度,也就是单位体积的电偶极矩,又称为电极化密度。该定义所指的电偶极矩包括永久电偶极矩和感应电偶极矩。电极化强度P、电场强度E、电位移D这三个矢量的关系表达式为
D=ε0E+P=ε0εrE
(2)
对于各向同性、线性电介质,电极化强度P和电场强度E的比例称为电极化率χe,有
P=χeε0E
(3)
所以,电位移与电场强度成正比,即
D=ε0(1+χe)E=εE
其中,ε为电容率(介电常数)。相对电容率εr(相对介电常数)与电极化率的关系为
εr=1+χe
电极化强度P、电场强度E、电位移D三个矢量的方向相同。电磁学所描述的物理量大部分都是宏观的平均值,像电场平均值、电极化强度平均值等都是取自一个远大于原子尺寸的区域。当研究微观问题时,对于在电介质内的单独粒子,其极化性与电极化率平均值、电极化强度平均值的关系可用克劳修斯-莫索提方程来表达:
(4)
式中,Nj为分子j的每单位数量的面积;αj为分子j的分子极化率。
式(4)表达了分子极化性与介电常数的关系。该式在微观量(极化性)和宏观量(介电常数)之间建立起了一个连接,是连接微观世界与宏观世界的“桥梁”。式(4)有助于在分子层面上进一步理解介电湿润芯片上液滴驱动的本质——固液接触面在电场下的作用机理。
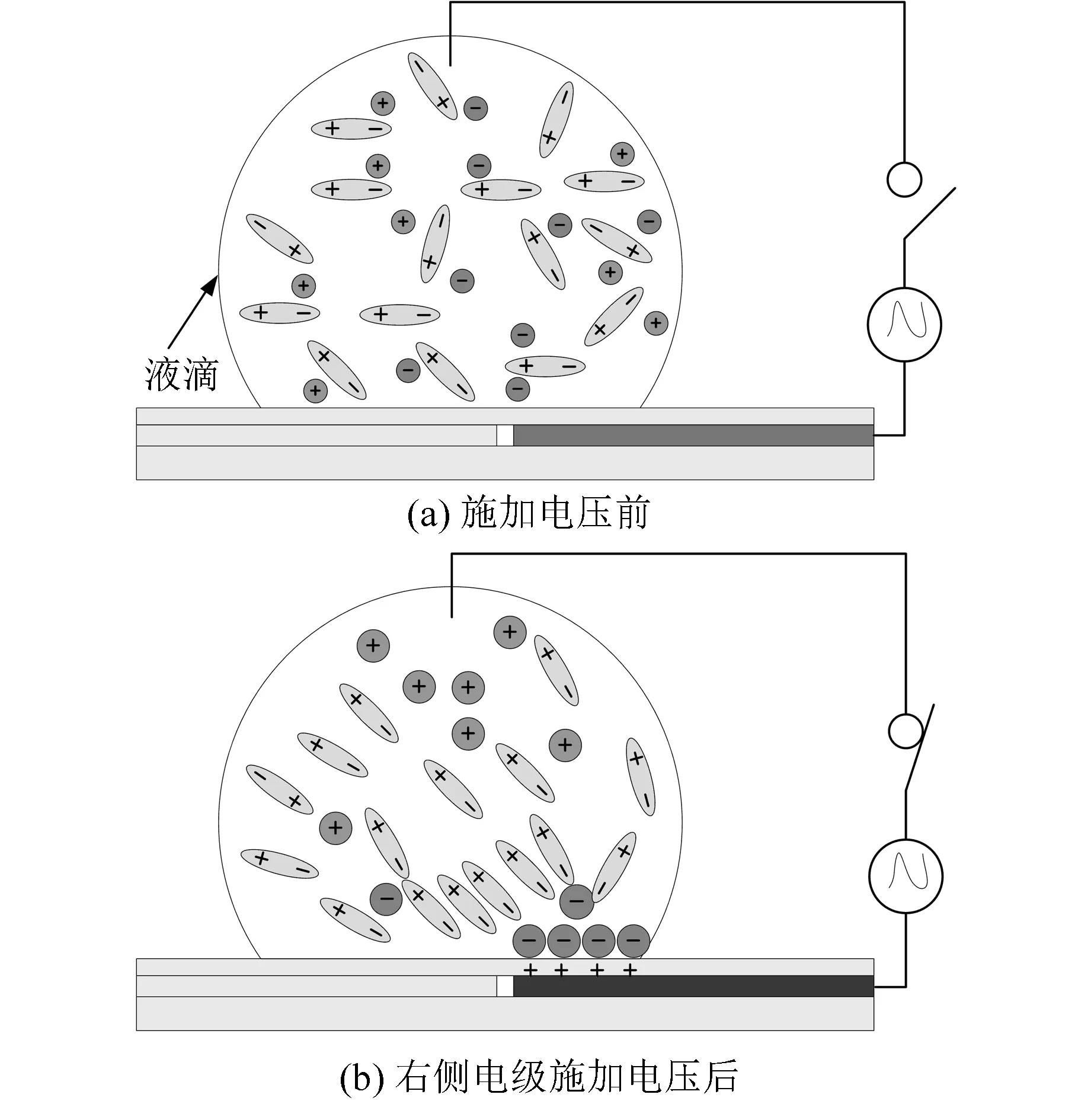
图2 电荷与电偶极子变化情况示意图(侧视图)Fig.2 Schematic diagram of the change in charge and electric dipole (side view)
在图2所示的EWOD芯片中,当右侧驱动电极不导通时(图2a),液滴中的电偶极子和自由电荷随机分布在液滴中。当右侧驱动电极导通时(图2b),在驱动电极与零电极之间形成电场,在电场作用下,厌水层表面会聚集大量的正电荷而成为表面束缚电荷,在这些表面束缚电荷的作用下,根据异性相吸的原理,液滴内靠近束缚电荷表面的带负电的自由电荷与电偶极子带负电的部分会被吸引到该表面。宏观上,液滴位于导电驱动电极上方的厌水层表现出亲水性,位于该部分之上的液滴接触角会减小。这一过程液滴受到静电力作用,静电力是导致液滴接触角改变的主要原因。
3 数值仿真及实验研究
3.1 介电驱动力
采用COMSOL Multiphysics 4.4多物理场仿真软件对图1b和图2b中的电场进行数值仿真,相关模型参数见表1。
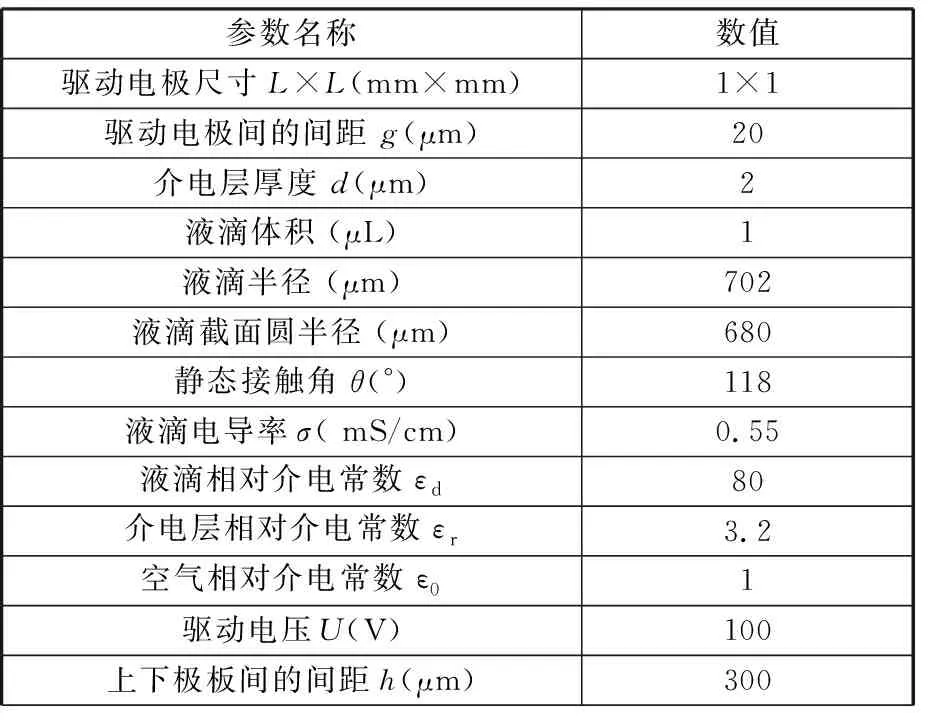
表1 数值仿真模型相关参数
在进行数值仿真时可把液滴近似看作介电体,根据电荷守恒定律和拉普拉斯方程[9]得到
(σU)=0
(5)
(6)
外加电压在液滴附近产生静电场,由该电场引起的介电驱动力分量为
(7)
式中,Fi为空间直角坐标系中第i个坐标的介电驱动力分量;Tij为麦克斯韦应力张量元;sj为第j个坐标方向上液滴的表面积;Σ表示积分区域为液滴表面。
由张量运算规则可知对于每一个麦克斯韦应力张量元,有
(8)
式中,Ei、Ej分别为空间直角坐标系中第i和第j个坐标方向的电场强度;δij为Kronecker函数。
由高斯环路定理可得麦克斯韦应力张量为
(9)
ε=εrε0
式中,I为二阶单位张量。
把麦克斯韦应力张量改写成矩阵形式如下:
T=
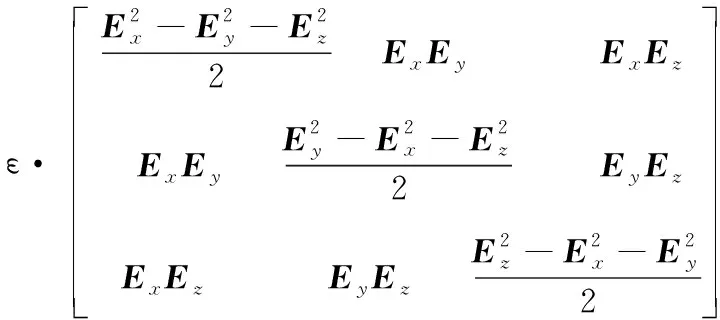
(10)
利用高斯定理求得图1中液滴在x、y、z三个方向所受介电驱动力为
(11)
式中,V为液滴的体积。
由于y、z方向的介电驱动力对液滴运动影响较小,可忽略不计,所以液滴所受介电驱动力可简化为液滴在x方向上的受力。
图3所示为“液滴-驱动电极-介电层-介质”所组成的系统划分好网格后的三维模型。为简化运算,本文数值仿真只选取了左右两个驱动电极,选择空气作为介质。
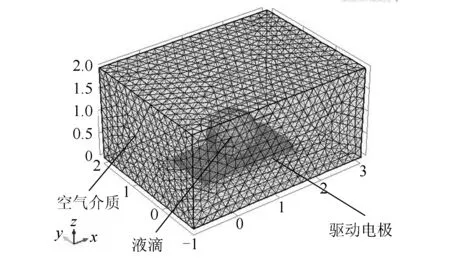
图3 液滴三维仿真模型Fig.3 Three-dimensional simulation model of droplet
图4a为右侧驱动电极导通时的电势分布图,为更直观地表示驱动电极导通后的电势分布情况,此图后处理过程中选择切片模式。很明显,右侧驱动电极上的电势接近100 V。图4b为固液接触面电场强度分布图,箭头的长短表示该箭头所处位置电场强度的大小,很明显,液滴截面圆位于右侧驱动电极之上的电场最强,该部分电场集中分布,电场的方向指向零电极。图4c为固液接触面上麦克斯韦应力张量分布图,箭头的长短表示麦克斯韦应力张量的大小,很明显,液滴截面圆位于右侧导电驱动电极之上的麦克斯韦应力张量是最密集和最大的。
根据麦克斯韦理论,电场是传递力的“桥梁”,电荷之间所产生的库仑力靠电场来进行传递。驱动电极导通时会在介电湿润芯片与液滴所组成的系统中产生电场,计算出总的电场分布之后就可以推导出麦克斯韦应力张量。根据上文液滴所受介电驱动力(式(11))可知,麦克斯韦应力张量是计算EWOD芯片中液滴所受介电驱动力的一个桥梁,计算出麦克斯韦应力张量,就可以算出液滴所受介电驱动力。同理,图4c把固液接触面上液滴受到的麦克斯韦应力张量用箭头直观地表示出来了,该结果和前文中液滴受到静电力的理论分析可以相互印证。
图4d为驱动电极表面的极化效应数值仿真图。在电场的作用下,介电层材料与液滴间会表现出异性电荷相互吸引的趋势。EWOD芯片系统中介电层材料与液滴的分子原来是没有电偶极矩的,在外电场作用下,构成分子的正负电荷发生相对位移,形成电偶极子,具有一定的电矩,其方向沿着外电场的方向,所以在固液接触面上,分别出现了正负束缚的表面电荷。图4d中的箭头正是把“极化”这一抽象概念形象地表示出来了,图中较大的箭头集中于液滴截面圆之内,这说明在电场的作用下该部分是有“极化效应”存在的。首先,位于导电驱动电极上方的固液接触面在电场的作用下产生“极化效应”,这一过程液滴受到静电力作用,然后,该部分固液接触面形成表面束缚电荷后使液滴的表面张力平衡状态遭到破坏,不再平衡的表面张力使液滴产生一定量的形变,液滴的形变会使液滴内部产生压力差,而该压力差即为驱动液滴运动的力。
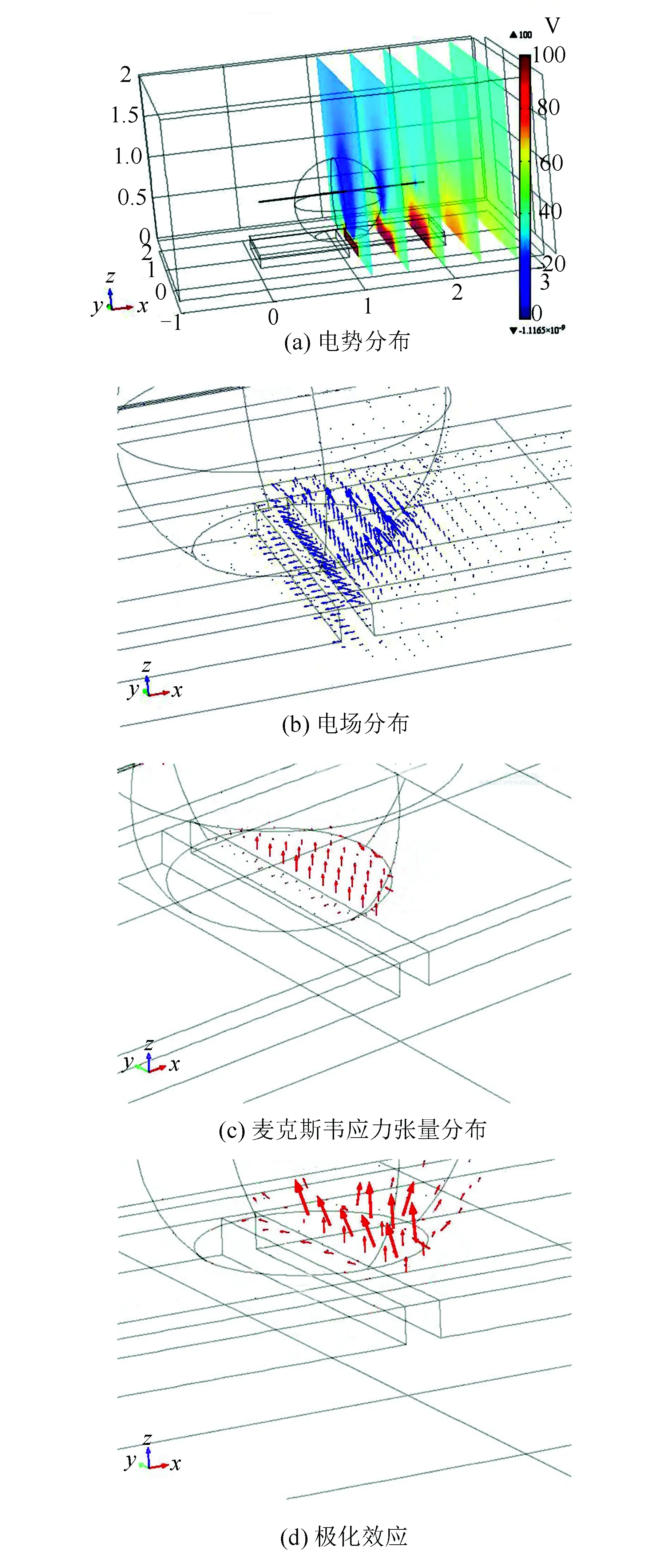
图4 电场数值仿真结果Fig.4 Numerical simulation results of electrical field
3.2 驱动机理及实验验证
图5a中,液滴恢复部分和前进部分的曲率半径分别为[17]
(12)
(13)
式中,θ0、θU分别为液滴恢复部分和前进部分的接触角,即初始接触角和施加驱动电压U时的接触角;θt为液滴与上极板接触时的接触角;h为上下极板间的间距。
根据拉普拉斯方程,位于液滴恢复部分与前进部分的两个随机点1和2处的压力p1和p2分别为
(14)
(15)
式中,R1、R2分别为液滴恢复部分和前进部分的半径;pg为空气介质压力。
那么可以推导出液滴内部1和2两个随机点处流体静压力差计算式为
(16)
由图5a可知,液滴恢复部分曲率半径小于前进部分曲率半径,即γ1<γ2;液滴恢复部分半径小于前进部分半径,即R1
pi≈p1-p2
此压力差计算式忽略液滴的接触角滞后和液滴周围介质对液滴的黏性阻力,是一个理想状态下的估算数学模型。
图5b为液滴内部压力最大区域随驱动时间在液滴内部转移示意图,1~4号四个虚线圆分别表示在不同时刻液滴内部压力最大区域。圆面积的大小表示压力最大区域的大小。如前所述,随着驱动时间的延长,液滴内部压力最大区域会依次从1~4四个位置进行不间断的转移,同时其面积也会不断增大。当液滴内部压力最大区域移动到4号圆所在区域时不会再继续移动,而是保持在此位置并呈现出面积扩大的趋势,此时液滴内部产生流体静压力差Δp,当Δp足够大时就可以驱动液滴向压力较小的方向运动。
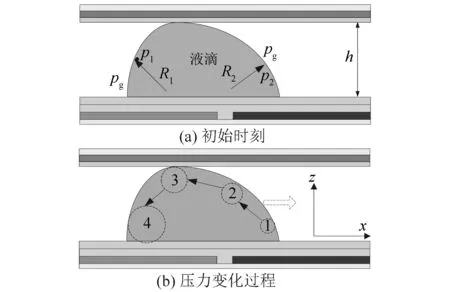
图5 压力最大区域变化示意图(侧视图)Fig.5 Schematic diagram of maximum pressure area changes (side view)
根据文献[19]中自由体表示法可以得到液滴在x方向所受“气-液”表面张力分量大小:Fx=γlgcosθU,综合以上分析,液滴在x方向所受介电驱动力、表面张力和流体静压力差近似相等,即其大小有如下关系:
Fx≈γlgcosθv≈Δp
(18)
在电场作用下,液滴从静止到运动的过程中其内部的自由电荷和电偶极子与芯片厌水层中的表面束缚电荷相互吸引,此过程中出现的一个明显变化是芯片的厌水层由厌水性变为亲水性,随着厌水层湿润性增强,液滴的相应部分会摊开,摊开部分的接触角减小,该摊开部分即为前进部分,这一过程中静电力占主导作用,液滴所受力即为介电驱动力Fx;然后,液滴前进部分和恢复部分不同的表面形状会使液滴产生形变,该形变会打破液滴原有的表面张力平衡状态,此时液滴恢复部分的接触角变化很小,可以忽略,表面张力占主导作用,液滴受到的表面张力大小为Fx。随后,液滴恢复部分的流体静压力大于前进部分的流体静压力,不平衡的表面张力会破坏液滴内部的压力平衡状态,因此,液滴内部会产生流体静压力差Δp,当Δp足够大时液滴就能够被成功驱动。
为验证液滴从静止到运动的机理,本文设计制作了介电湿润芯片。选用ITO玻璃作为芯片的基底,通过湿法刻蚀技术在ITO玻璃上制作出驱动电极。阵列驱动电极上驱动电极数为5,驱动电极尺寸为1 mm×1 mm,驱动电极间的间距为20 μm。选用SU-8光刻胶作为芯片的介电层,芯片介电层厚度为2 μm,其介电常数为3.2。使用双面胶带固定芯片上下极板,上下极板间距为300 μm,实验过程中使用微量注射器把1 μL去离子水液滴置于芯片上。实验室温度为24 ℃,忽略液滴蒸发的影响,芯片具体制作工艺及实验平台搭建详见文献[10,22]。由于ITO玻璃具有较好的透光性,同时SU-8光刻胶烘干后变得透明,图6a中用虚线表示的芯片中的驱动电极可见。图6中,去离子水液滴前进部分位于导电驱动电极之上;液滴恢复部分位于非导电驱动电极之上,同时,该部分形状保持原状。这个过程中,液滴前进部分与恢复部分的表面强力非对称的改变使得液滴产生一定程度的形变,此时,液滴非对称的形变会在液滴内部产生流体静压力差。当液滴内部的流体静压力差足够大时,液滴就能够成功地由静止状态被驱动,当依次给阵列驱动电极施加一定量的驱动电压时,液滴就能够沿着阵列电极进行连续运动。
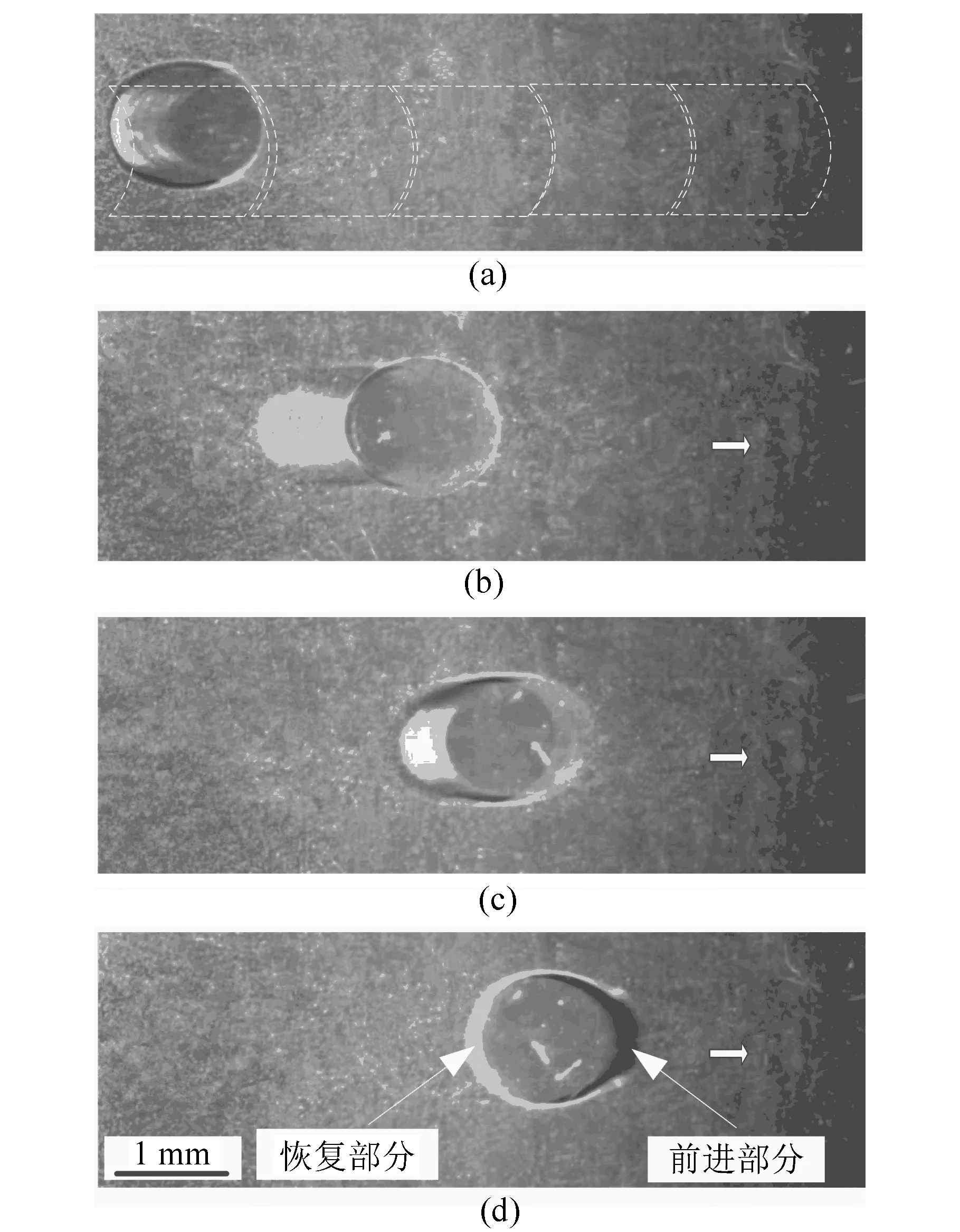
图6 1 μL去离子水液滴运动视频截图(俯视图)Fig.6 Video frame images of the 1 μL deionized droplet motion (top view)
综上所述,介电湿润芯片上液滴从静止到运动需要依次经历以下4个过程:
(1)把“EWOD芯片-液滴”看作是一个电容系统。当驱动电极导通时,位于导电驱动电极上方的液滴初始接触角减小。
(2)接触角减小会改变液滴的表面张力,而驱动电极不导通,则电极上方液滴的初始接触角保持不变,其表面张力也保持不变。
(3)液滴前进部分与恢复部分的表面张力非对称改变会使液滴发生一定量的形变。
(4)一定量的液滴形变会在液滴内部产生流体静力压力差,当流体静力压力差足够大时就可成功驱动液滴。
4 结语
本文研究了介电湿润芯片上固液接触面表面束缚电荷作用机理;数值仿真了“EWOD芯片-液滴”系统中的电场,数值仿真结果和讨论表明电场形成后在固液接触面上的正负离子、分子相互吸引产生静电力,该静电力使液滴表面张力发生改变;而左右两侧非对称的表面张力会使液滴产生形变,一定量的液滴形变会在其内部产生流体静力压力差,而足够大的流体静力压力差会成功驱动液滴从静止到运动;最后,通过1 μL去离子水液滴运动实验对液滴从静止到运动的过程和机理进行了验证。为简化模型和降低运算量,本文在进行数值仿真时忽略了液滴的蒸发及接触角滞后与饱和效应对介电驱动力的影响。本文从本质上解释了液滴从静止到运动的过程,分析了液滴被成功驱动的机理,为更好地理解和利用数字微流控技术奠定了一定的理论基础。
