考虑结合面法向刚度的拉杆转子轴向振动特性

何 谦 王艾伦 陈中祥 杨 俊

1.湖南师范大学工程与设计学院，长沙，410081 2.中南大学高性能复杂制造国家重点实验室，长沙,410083

0 引言

拉杆转子具有质量小、刚度大、加工容易以及便于冷却和维修等突出优势，被广泛应用于航空发动机及大功率重型燃气轮机中[1]。不同于整体转子，拉杆转子通过周向均匀分布的多根拉杆将轴头和轮盘预紧连接而成，因而在结构上存在多个非连续的接触界面，物理特性非常复杂。由于接触问题的本质是非线性的，零件的材质、表面形貌、载荷情况等因素都会对结合面的接触状态和接触刚度造成影响[2]，很难用一个统一的模型加以描述，这给拉杆转子的深入研究带来了巨大的困难。现阶段对接触问题的研究主要有两种方法，即建立解析模型和开展数值计算。解析的方法通常依托Greenwood等在1966年提出的GW 模型以及以其为基础的各种改良模型，如MB 分形接触模型、GW 修正模型等。以上模型都基于某些假设，而且在参数的确定上需要依托实验和统计的数据，操作起来比较困难[3]，结果的精度也难以保证。随着计算机技术的飞速发展，以有限元为代表的数值计算方法在接触分析中得到了越来越广泛的应用[4]，其参数化的设计方法不仅能方便高效地获取实验样本，而且更容易发现或形成规律性的认识和结论。将其运用于拉杆转子的动力学特性分析，成效显著[5-7]。

由于弯曲振动是拉杆转子动力学特性中最为重要的环节，故在业已开展的研究中，绝大部分都是针对这一问题进行的。事实上，拉杆转子的轴向振动问题也不容忽视。据报道，2001年广东月亮湾燃机电厂燃气轮机发电机组投产一周后，就出现了机组转子因轴向振动剧烈而导致的故障[8]。早在20世纪50年代，燃气轮机转子的轴向振动问题就引起人们注意[9]，但由于检测困难等原因，研究未能深入。目前，国内外对转子轴向振动问题的研究相对较少，而关于拉杆转子轴向振动问题的研究更少。文献[10]用传递矩阵法对多轮盘转子系统轴向振动的固有特性进行了研究，但其研究对象为整体转子。文献[11]运用键合图的方法建立了拉杆转子轴向振动的动力学模型，但该方法界面接触刚度计算方面主要参照了文献[12]的结论，给出的轮廓面积比ηca在某一范围内，实际确定起来比较复杂。

本文在分析和总结现有研究成果的基础上，提出了一种基于有限元分析结果的轮盘结合面法向接触刚度的确定方法，将其与转子的集中质量模型结合，计算了某型实验转子轴向振动的固有频率，通过对比理论计算和实验实测的结果，验证该方法的有效性。

1 轮盘结合面法向刚度的确定

1.1 三维粗糙表面的生成

THOMAS等[13]已证明指数自相关函数能够很好地描述现实世界中的许多随机现象；WHITEHOUSE等[14]通过实验证明了许多工程表面轮廓具有指数自相关函数关系。一般给定指数形式的自相关函数为

τx=1,2,…,Nτy=1,2,…,N

式中，σ为表面粗糙度；βx、βy分别为x、y方向上的相关长度。

根据轮盘表面的粗糙度数值，按指数自相关值，以粗糙度Ra=3.2 μm为例，在MATLAB中生成相应的微观表面，见图1。

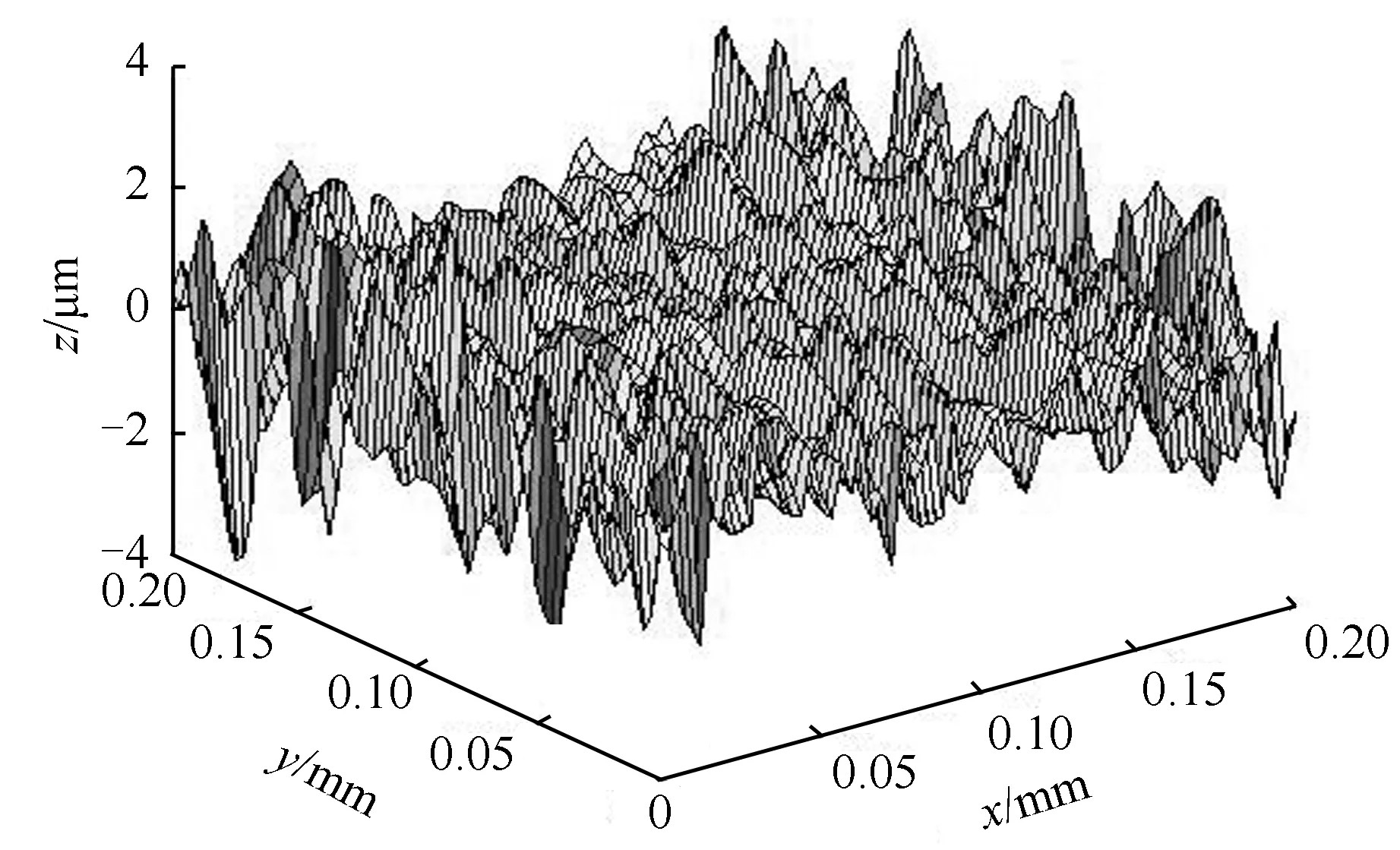
图1 微体单元粗糙表面形貌Fig.1 Rough surface features of the microbody

1.2 基于微体单元的结合面法向刚度的确定

由于零件的宏观尺寸均远远大于用以描述表面形貌的参数尺寸，故如果考虑表面的微观形貌直接对零件开展有限元分析，将会导致单元和节点的数目巨大，可能会因计算量过大而无法进行。当粗糙表面微型长方体的宏观尺寸达到一定数值时，所得的分析结果与继续扩大微体尺寸并无二致[15]，因此，借助具有合适几何尺寸的微体单元，所得的结果完全能反映实际零件的接触情况。据此将MATLAB中所获得的点云数据导入CAD软件中，生成一个左端面为粗糙表面的微型长方体，3个方向的尺寸分别为1 mm×1 mm×5 mm。

考虑到两粗糙表面微元体接触和单个粗糙面与刚性平面接触的分析结果在保证微体单元足够长度后并无差别[16]，本文直接采用相对简单的微体单元与刚性平面接触的分析方法。将CAD中生成的模型导入ANSYS，网格划分采用10节点四面体单元，微体单元定义为弹塑性，各项力学指标依据轮盘材料给定。分析时，对长方体的底面加以约束，并限制粗糙表面上位于刚性平面内的节点的位移。在与粗糙表面相对的右端面上，施加一个由转子预紧力转换而成的分布力p。查看分析结果，获得微体单元在该方向的变形量，由此获得整个微体单元在该作用力下的等效法向刚度keq：

keq=pA/Δl

式中，A为微体单元的横截面面积；Δl为微体单元在该方向的变形。

依据圣维南原理，粗糙表面的变形情况对距离其较远区域的影响很小。据此可按有限元软件的分析结果将微体划分为粗糙段和光滑段两部分，粗糙段为微体单元受力时发生塑性变形的区域，用lc表示；余下部分视作只发生弹性变形，用ls表示，见图2。

图2 微体单元等效模型Fig.2 Equivalent model of the microbody

显然，微体单元在不同载荷作用下的粗糙段lc的长度也不相同。改变压力p，得到lc与p的变化关系曲线，见图3。

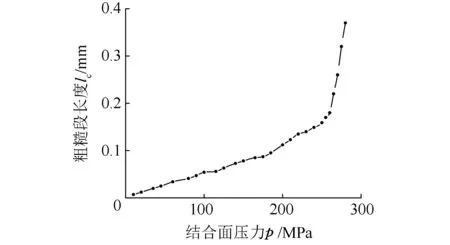
图3 粗糙段长度与作用力的关系曲线Fig.3 Relation curve of rough section length & press

由材料力学可知，弹性轴段ls的法向刚度

ks=EA/ls

式中，E为轮盘材料的弹性模量；ls为弹性光滑段的长度。

用kc表示粗糙段的刚度。显然，微体单元各段的刚度kc、ks和等效法向刚度keq三者之间存在以下关系：

联立以上各式，即可求得粗糙段的刚度kc。

定义kj为轮盘结合面的法向刚度。考虑到实际情况为两粗糙表面接触，故有

kj=kc/2

2 拉杆转子轴向振动集中参数模型

尽管不同厂家及不同型号的拉杆转子在几何尺寸上差异明显，但转子的组成和结构却基本相同，即均通过长螺栓将轴头和轮盘串连而成。为方便说明和计算，本文对拉杆转子的形态进行了适当简化，其物理结构见图4。

图4 拉杆转子结构示意图Fig.4 Schematic view of the rodfastening rotor

2.1 拉杆转子质量的集中参数化

结合轴向振动分析的要求以及拉杆转子的结构特点，选取单个轮盘作为基本单元进行集中参数化：将轮盘的质量集中到两端，将其变形集中到中间。轮盘之间的接触刚度用一根无质量的弹簧表示。拉杆处理方式与轮盘类似。需要注意的是，由于位居拉杆两端的螺栓头和螺母与轴头没有相对运动，故可将拉杆的集中质量看作与两轴头外侧的质量单元固连在一起。相应的力学模型见图5。

图5 拉杆转子轴向振动集中质量模型Fig.5 Lumped-mass model of the rodastening rotor axial vibration

图5中，kd、krod、kj分别为轮盘、拉杆以及轮盘接合面的法向刚度。kd、krod的确定不考虑塑性变形的影响，依据式(4)和零件的材料和几何尺寸获得，其中，krod为所有拉杆的刚度之和。

2.2 数学模型的建立

由于转子系统一般都是弱阻尼系统，故在建模和计算过程中可以不计阻尼。依据图5中的集中参数模型，写成矩阵的形式，即

X=[x1x2…x2n]TF=[f1f2…f2n]T

K=

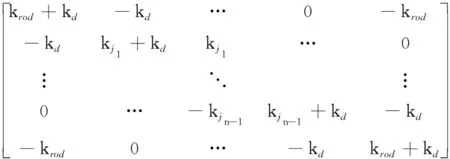
据此可以求得拉杆转子轴向振动时的固有频率和振型[17]。

3 实验及数据分析

实验用拉杆转子由4轮盘8拉杆组成，每根拉杆的预紧力为4 kN，轮盘的大圆直径与中心孔直径分别为100 mm和40 mm，轮盘厚度为30 mm，拉杆的直径为10 mm，轮盘中心与拉杆中心的距离为35 mm。为排除支承的影响，用两根绕在转子轴头的弹性绳将转子水平自由悬挂。用力锤沿轴线方向敲击转子的端面，用压电加速度计测量响应，并借助信号分析处理系统获得转子的固有频率和振型。

为验证2.2节转子模型的有效性，将实验转子的相关参数代入该模型进行计算。作为对比，还建立了同形态整体转子的有限元模型。3种渠道所获得的该型转子前3阶轴向振动的固有频率见表1。

表1 轴向振动固有频率比较 (预紧力为4 kN)

为研究拉杆预紧力对拉杆转子动力学行为的影响，采用1.2节的方法，从零开始逐步加大拉杆的预紧力，得到轮盘结合面法向刚度随作用力(压力)变化的曲线,见图6。将该结果代入集中质量模型进行计算，得到该型转子在不同预紧力作用下的前3阶固有频率,见图7。

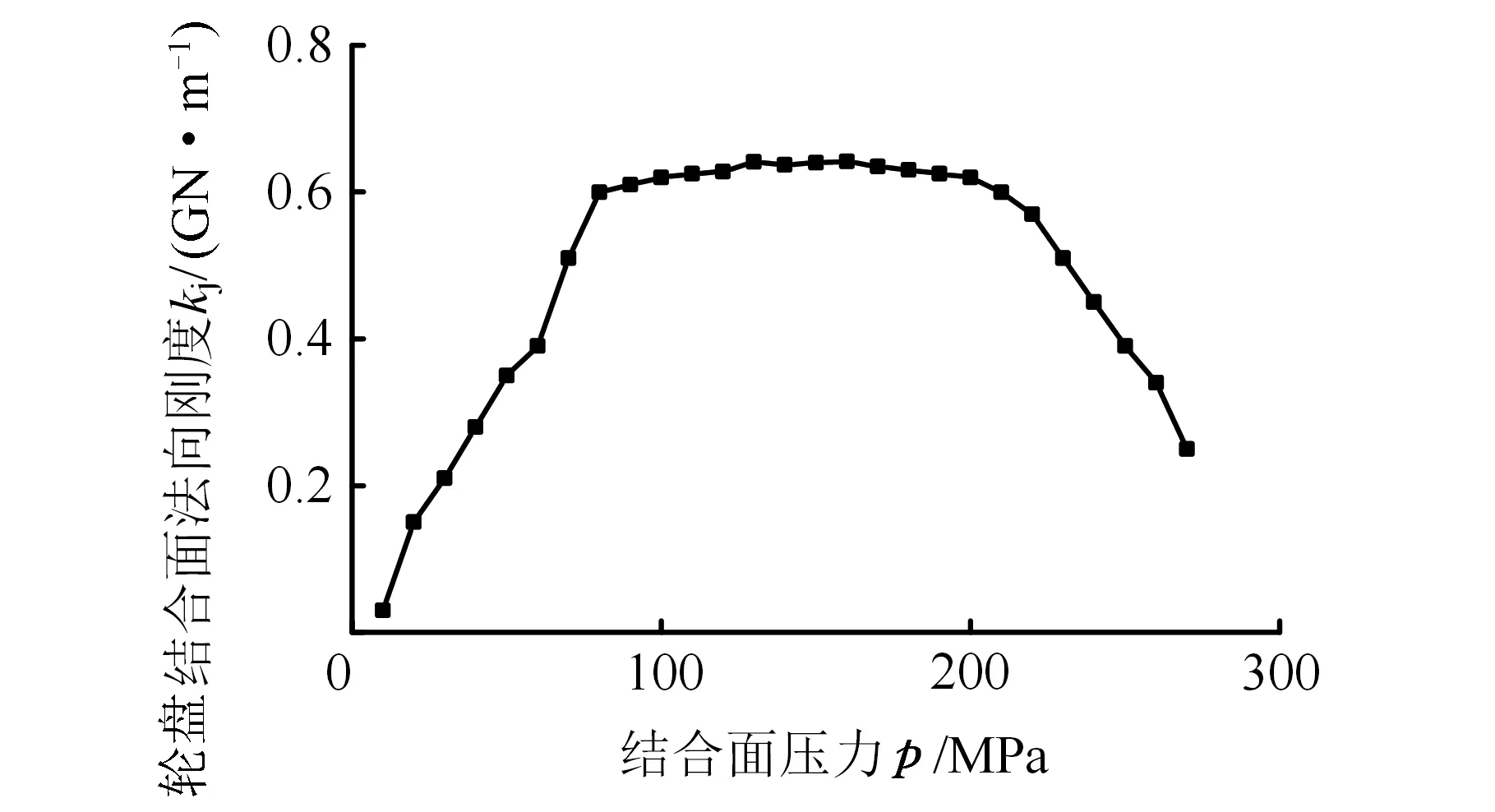
图6 结合面法向刚度与压力的关系曲线Fig.6 Relation curve of the contact surface normal stiffness & press

图7 固有频率与结合面压力的关系曲线Fig.7 Relation curve of the natural frequency & contact surface press

从表1中数据可以看出，拉杆转子与具有相同外部形态的整体转子的固有频率差距明显，而实验实测值与用本文方法计算所得的结果非常接近,误差在5%范围内，远低于整体转子模型误差。这表明对拉杆转子开展动力学特性分析，必须考虑结合面法向刚度的影响。

由图6和图7可知，拉杆转子轮盘结合面的法向刚度和轴向振动的固有频率主要取决于拉杆预紧力的大小，但它们之间并非简单的线性关系。特别需要注意的是，当预紧力达到一定数值(对应图6中约100 MPa处)后，增大预紧力，结合面刚度和固有频率的变化很小，即进入所谓的预紧力饱和阶段[18]。在这一阶段，拉杆转子的固有频率与整体转子趋于一致[11]。进一步加大拉杆的预紧力，当结合面间的压力超过200 MPa时，无论结合面刚度还是固有频率都呈现下降的态势，其原因是压力值超出了轮盘材料的屈服极限，导致发生塑性变形的区域迅速扩大(见图3)。此外，比较转子各阶次固有频率随结合面法向刚度变化的情况可以发现，低阶频率曲线从形态上与刚度曲线吻合程度更高，表明结合面刚度对低阶次固有频率的影响较大，而高阶次频率反映了转子整体刚度的变化。

4 结论

(1) 具有相同外部形态的拉杆转子和整体转子在动力学行为上存在较大的差别，分析拉杆转子的动力学特性必须考虑轮盘结合面法向刚度的影响。用本文方法得到的实验转子的轴向振动固有频率数值与实验实测值非常接近，误差低于5%，表明该方法切实可行，并且具有较高的精度。

(2) 拉杆的预紧力直接影响轮盘结合面的法向刚度和转子的固有频率，但并不一直随着拉杆预紧力的增大而增加，而是存在预紧力饱和阶段。处于这一阶段的拉杆转子的固有频率也与整体转子趋于一致。

(3) 可借助结合面法向刚度的分析获取拉杆转子预紧力饱和的范围，此范围可以作为合理确定拉杆预紧力的数值以及保证拉杆转子结构完整性的重要设计依据。